雙曲率組合結構自由振動特性分析

龐福振 李海超 彭德煒 霍瑞東 繆旭弘

摘要：針對雙曲率組合結構自由振動特性分析方法有待完善等問題，基于半解析法開展了雙曲率組合殼結構自由振動特性研究。基于Flugge薄殼理論，首先將拋物殼-圓柱殼-球殼組合結構在交界面處進行分解，獲得拋物殼、圓柱殼和球殼子結構;再將拋物殼、圓柱殼和球殼子結構沿周向進一步分解為若干殼段，用沿徑向的Jacobi多項式和周向的Fourier級數來表示各個殼段的位移函數，并用不同的彈簧剛度對組合結構的邊界條件和殼體內的連續性條件進行模擬;最后，基于Rayleigh-Ritz法獲得雙曲率組合結構的振動模態，探索復雜邊界條件下雙曲率組合結構自由振動特性。在此基礎上，將雙曲率組合結構自由振動頻率與已有文獻及有限元法計算結果進行對比分析，驗證了方法的收斂性和有效性，研究成果可為復雜邊界條件雙曲率組合結構自由振動特性分析提供方法依據和數據積累。

關鍵詞：結構振動;自由振動;半解析法;雙曲率組合結構;復雜邊界條件

中圖分類號：O327;TB123文獻標志碼：A 文章編號：1004-4523（2020）03-0441-09

DOI：10.16385/j.cnki.issn.1004-4523.2020.03.001

引言

拋物線殼、圓柱殼及球殼組合結構在機械工程、船舶工程、航空航天及土木工程領域應用廣泛。開展復雜邊界條件下拋物殼-圓柱殼-球殼（PCS）組合結構自由振動特性研究，明確其自由振動特性規律，對豐富雙曲率組合結構基礎理論及指導工程應用具有重要的意義。在此研究方面，Shang基于Love殼體理論分析了球殼一圓柱殼組合結構的自由振動。Saunders等采用Raylcigh-Ritz法得到了圓柱殼-圓錐殼組合結構的固有頻率。Tavakoil等運用Pade近似矩陣求冪的方法研究軸對稱殼結構的自由振動。Gallctly和Mistry以一端固定，另一端由旋轉殼體（圓錐殼、半球殼等）封閉的圓柱殼組合結構為研究對象，采用有限差分法和有限元法分析了其自由振動。Lcc等運用Rayleigh-Ritz方法研究了球殼-圓柱殼結構在不同邊界條件下的自由振動。Ma等通過運用Fourier-Ritz方法研究了圓柱殼結構及一般邊界條件的圓錐-圓柱殼的組合殼結構的振動特性。瞿葉高等運用區域分解法研究了圓錐殼、圓柱殼及球殼組合結構及環肋圓柱殼-圓錐殼組合殼結構的振動特性。

由上述分析可知，一方面現有文獻大多聚焦于單個或一些簡單的組合殼結構，鮮有學者開展雙曲率組合結構振動特性研究;另一方面，已有文獻在位移函數選取方面大多考慮特殊形式的多項式，尚未形成統一、選擇范圍更廣的位移容許函數構造形式。為此，本文在區域分解法研究的基礎上，對位移容許函數進行改進，使組合殼結構位移函數較其他半解析法更容易選取;在此基礎上，開展拋物殼-圓柱殼-球殼組合結構自由振動特性分析，旨在為復雜邊界條件下拋物殼-圓柱殼-球殼組合結構自由振動特性分析提供方法依據和數據積累。

1理論方法

1.1數學模型

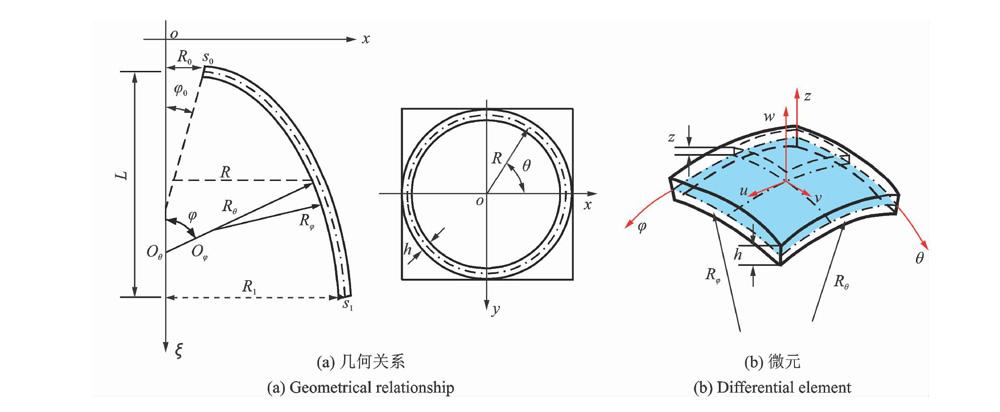
拋物殼結構是由拋物線繞中心軸旋轉而成，拋物殼幾何結構如圖1所示。

如圖1所示，厚度為h的旋轉殼結構由母線s₀s₁繞軸Oξ旋轉而成。L為旋轉殼總長，φ為徑向角度，θ為周向角度，R_φ為徑向曲率半徑，R₀為周向曲率半徑，R為水平半徑，且R_θsinφ。對于拋物殼，其幾何表征參數為

式中 k為拋物殼徑向特征參數

拋物殼-圓柱殼-球殼組合結構剖面圖如圖2所示。

假設組合殼結構由均質和各向同性的材料組成，左右殼結構由球坐標系O_l，r-φ_l，r，θ_l，r，Z_l，r描述，其中φ為徑向坐標，θ為圓周坐標。R_r和R_l為左右殼邊界半徑，L_r和L_l為左右殼的軸線長度。中間圓柱殼用柱坐標系（O_c-x，θ_c，Z_c）表示，其半徑為R_c，長度為L_c。每個殼結構的位移分量分別用u_ξ，v_ξ和w_ξ（ξ=l，r，c）表示，其中下標分別表示左側、右側及中間圓柱殼體。本文基于區域分解法，為精確獲得組合結構高階振動響應，將組合結構沿周向在交界面處劃分為幾個典型子結構，再在此基礎上，將子結構沿徑向方向進一步分解為N_l，N_c，N_r個殼段。

1.2 殼結構的能量傳遞

基于Kirchhoff假設和Fluggc的薄殼理論，子結構ξ第i殼段中性面處的應變-位移關系為

1.3 雙曲率組合結構的邊界條件和連續性條件

本研究基于懲罰函數對雙曲率組合結構的連續性條件和邊界條件進行模擬。其中懲罰參數由各個方向上彈簧的剛度值定義，這樣雙曲率組合結構的復雜邊界條件和連續性條件可以通過對懲罰函數設定適當的彈簧剛度值來實現，這也一定程度上方便了復雜邊界條件的模擬，是本文的主要優勢之一。

基于懲罰參數，存儲在邊界彈簧中的勢能可表示為

1.4 位移函數和矩陣方程

選擇適當的位移函數對求解的精度有較大影響，本文在區域分解法的基礎上，將切比雪大多項式擴展為統一的、選擇范圍更廣的Jacobi多項式。這也是本文較改進傅里葉法、區域分解法等半解析法最突出的優勢。雙曲率組合殼結構軸向與徑向位移函數分別用Jacobi多項式和Fouricr級數來表示，而Jacobi多項式定義在區間∈[-1，1]內，第i階Jacobi多項式P_i^{（α，β）}（φ）可表示為

式中

K，M和E分別為組合殼結構的剛度陣、質量陣和未知系數矩陣。通過求解方程（23）可求得組合殼結構的特征頻率和特征向量。

2 數值分析

2.1 收斂性分析

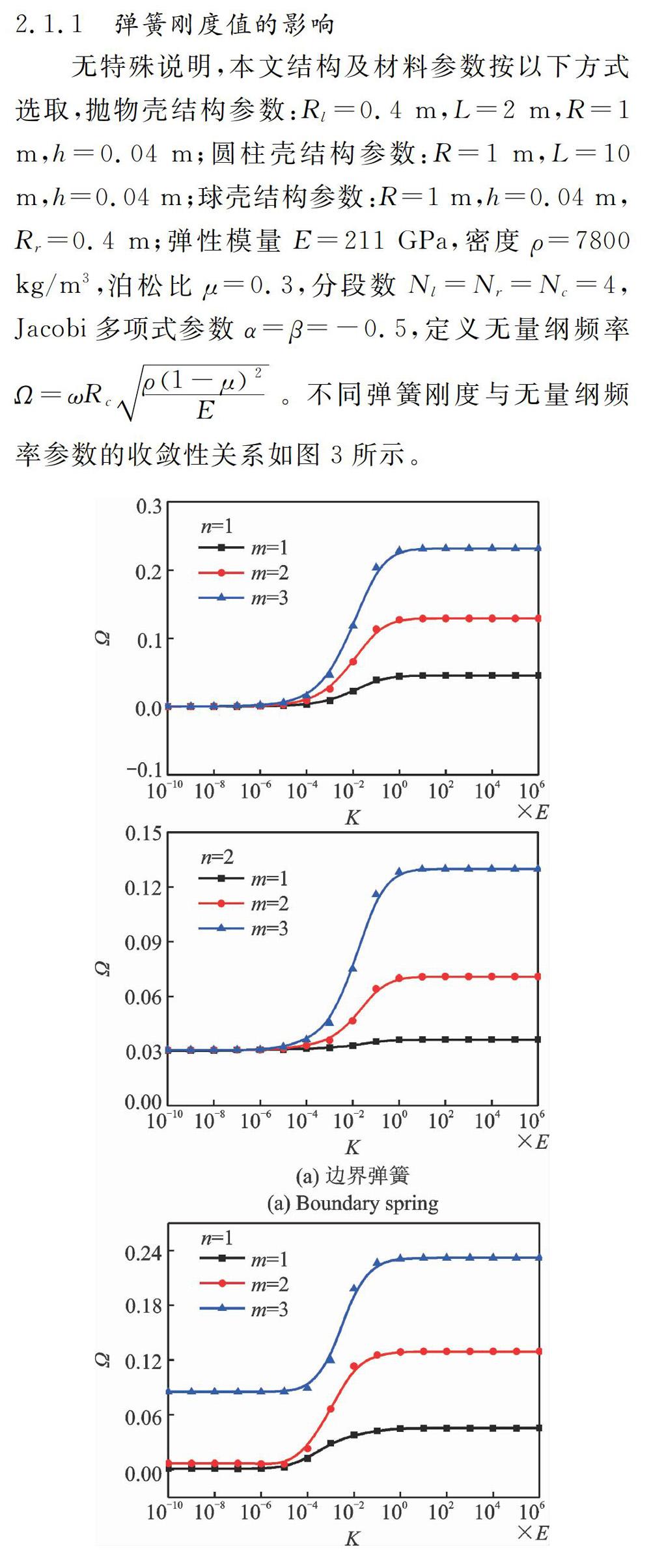
2.1.1 彈簧剛度值的影響

由圖3可知，彈簧剛度取值K_t≥10²E時，組合殼結構收斂，可視為剛性邊界條件;彈簧剛度為零時，可視為自由邊界條件;彈簧剛度10^-4≤k_t≤10^-1E可視為彈性邊界條件。滿足復雜邊界的彈簧剛度值可定義為如表1所示形式。

2.1.2 殼段數的影響

為方便與文獻對比，本文計算模型采用與其相同的幾何和材料屬性參數。Jacobi參數取為α=β=-0.5.自由邊界條件下，球殼-圓柱殼-球殼結構無量綱頻率與殼段數關系如表2所示。

由文獻可知，分段數的選取主要與結構主尺度、曲率變化及計算頻率等有關。且結構主尺度越大、曲率變化越大、計算頻率越高，求解精度對結構分段數要求越高。由表2可知，對球-柱-球組合結構，當結構分段數不小于4時，本文計算結果已收斂且與文獻結果一致性較高。故在下文計算中，統一選取雙曲率組合結構各個子結構的分段數為4.

2.1.3 Jacobi多項式參數的影響

與2.1.1結構和材料參數相同情況下，取分段數N_l=N_r=N_c=4，以α=β=-0.5為基準來衡量其他Jacobi多項式參數的相對誤差。

由圖4可知，其他參數一定條件下，改變Jacobi多項式參數α和β對雙曲率組合結構自由振動頻率影響較小，不同Jacobi參數下的最大相對誤差不超過2×10^-5。也就是說，不僅是特殊的勒讓德多項式或切比雪大多項式可用于位移函數的構造，所有Jacobi參數下的多項式均可用來構造位移函數。該發現不僅形成了位移函數的統一形式，還在一定程度上擴展了位移容許函數的選取，這也是本文較其他半解析法最突出的優勢。

2.2 有效性驗證

為驗證本文方法的有效性，將典型邊界條件（F-F，F-C，C-C）下拋物殼-圓柱殼-球殼組合結構頻率參數與有限元仿真結果進行比對。組合結構有限元（ABAQUS）分析網格類型為S4R，網格數量邊長尺度為0.07m，對比結果如表3所示。

由表3可知，對周向模態n（n=1，2，3），前4階軸向模態計算結果與有限元法吻合較好，表明本文方法可用于一般邊界條件下雙曲率組合結構自由振動特性分析。

2.3 復雜邊界條件下組合殼結構振動特性分析

基于上述研究，開展復雜邊界條件下拋物殼-柱殼-球殼組合結構自由振動特性分析，不同邊界條件下的計算結果如表4和5所示。

由表4和表5可知，當組合殼結構分段數目一定時，邊界條件對低周向波數的頻率參數有顯著影響，但隨著周向波數的增加，邊界條件的改變對組合殼結構振動特性的影響逐漸減小;同一周向模態下，組合殼結構頻率參數隨軸向波數的增加而增加。

3結論

本文基于Fluggc薄殼理論，提出一種半解析法，開展了復雜邊界條件下雙曲率組合結構自由振動特性分析。通過本文研究，可得如下主要結論：

1）拋物殼-圓柱殼-球殼組合結構的收斂性與彈簧剛度值、子結構殼段數以及Jacobi多項式參數等有關。當彈簧剛度值尾k_t≥10²E時，組合殼結構收斂，可視為剛性邊界條件;當彈簧剛度值k_t=0時，可視為自由邊界條件;當彈簧剛度值10^-4E≤k_t≤10^-1E可視為彈性邊界條件。子結構殼段數劃分越多，組合殼結構收斂性越好，計及求解效率等因素，子結構殼段數劃分不宜過大。Jacobi多項式參數對組合殼結構求解結果影響較小，可忽略不計。

2）經典邊界條件下，基于Jacobi-Ritz法的拋物殼-柱殼-球殼結構振動特性分析結果與現有文獻及有限元法結果吻合較好，驗證了本文方法的有效性。

3）本文基于Jacobi-Ritz法為復雜邊界條件下拋物殼-圓柱殼-球殼組合結構自由振動特性分析提供了數據積累及方法依據。