基于電流積分計算磁矢量勢修正的低磁雷諾數方法

丁明松 江濤 劉慶宗 董維中 高鐵鎖 傅楊奧驍

(中國空氣動力研究與發展中心計算空氣動力研究所,綿陽 621000)

針對低磁雷諾數方法的適用性問題,分析了當前低磁雷諾數條件應用上存在分歧以及全磁流體力學方法在高超聲速領域局限性產生的原理.在低磁雷諾磁流體力學控制數值模擬方法的基礎上,基于感應電流積分計算磁矢量勢,考慮截斷因子對計算域的縮減,提出了一種考慮感應磁場修正的低磁雷諾數磁流體力學計算方法,并加以驗證.結合RAM-C鈍錐體試驗飛行狀態數值模擬,分析了“忽略感應磁場”造成的計算偏差,探討了“低磁雷諾數假設”在高超聲速領域的使用原則.研究表明: 1)本文建立的修正計算方法,突破低磁雷諾數條件的限制,拓展了低磁雷諾數方法在高超聲速領域的適用性和應用范圍,數值模擬結果可信度高,同時通過積分區域限制等方法使計算效率得到了較大的提升;2)高超聲速流動過程中感應磁場的影響,在宏觀上表現為對外加磁場的削弱和扭曲,一定程度上降低了磁控效果;本文計算條件下,“Rem <0.1”的低磁雷諾數條件可能過于保守,建議取為Rem <1.0,同時其特征電導率和特征尺度應綜合考慮實際的等離子體分布.

1 引 言

早在二十世紀五六十年代,人們就開始了磁流體力學 (magnetohydrodynamic,MHD)的研究.上世紀九十年代以來,隨著高超聲速飛行技術、計算機技術和便攜磁體制造業的發展,高超聲速磁流體力學控制掀起了新的研究熱潮.在飛行器不同部位加載合適的磁場發生裝置,通過動量和能量的輸運對高超聲速飛行器周圍的流動狀態進行控制,顯著地改進和提升飛行器的氣動力/熱特性、電磁通信性能、隱身與突防特性等,這就是高超聲速磁流體力學控制[1].高超聲速磁流體控制技術已經成為一個多學科交叉融合的重要研究方向,其應用前景十分廣泛,可用于飛行器氣動熱環境管理、氣動力操控、等離子體電子數密度控制、流速控制和邊界層控制等多個方面[2].由于它具備不改變飛行器外部結構、無需機械傳動、響應快速準確、兼容性強等優點,因而受到世界各國高度重視.

數值模擬是研究高超聲速磁流體力學控制的主要手段之一.從高超聲速磁流體力學的國內外發展狀況可以看出,當前高超聲速MHD數值模擬的方法主要有兩種[1,3]: 全MHD方法和低磁雷諾數MHD方法(或簡稱低磁雷諾數方法).

全MHD方法[4,5]是通過廣義歐姆定律和安培環路定理消去流動控制方程和麥克斯韋方程組中電場E和感應電流J,然后將流動控制方程和磁擴散方程(由法拉第定律得到)聯立構成全MHD方程組,求解該方程組得到磁流體流場和感應磁場分布.在此基礎上,可通過求解電流連續性方程和廣義歐姆定律,得到電場和電流分布.全MHD方法理論上適用于各類磁流體的數值計算分析,但在高超聲速飛行器流場(尤其是外流場)MHD數值模擬方面存在很大困難[1,2].

與其他領域不同,高超聲速飛行領域磁流體力學控制具有其自身的特點.由于高超聲速飛行器外流場等離子體磁導率小、導電性一般較弱,電磁場變化的特征時間遠小于流動的特征時間,因此數值模擬飛行器高超聲速流場磁流體流動時常采用“低磁雷諾數近似”: 在磁導率、電導率較小時,感應磁場相對于外加磁場很弱,基本上可以忽略,此時可以假設磁場未受流動干擾,舍去電磁交叉項,使數值模擬過程得到簡化,這就是低磁雷諾數MHD方法.對于穩態(或準穩態)高超聲速磁流體流動,采用低磁雷諾數方法,可以有效地避免偽磁場散度和低電導率帶來的剛性問題,減小了非必要的繁復計算,這是業內通行的做法之一.國內外很多高超飛行器磁流體力學控制方面的研究,如日本的Nagata等[6]、Otsu[7]、Fujino 等[8]和 Takahashi等[9],美國的Bisek等[10,11]和Lee等[12],意大利的Cristofolini等[13,14],國內的李開等[15,16]、姚霄等[17]、潘勇[2]、張向洪[3]、何淼生等[18]、陳剛等[19]以及孫曉輝[20]等,在針對“低磁導率、低電導率特征”氣體的數值模擬時,也幾乎都采用低磁雷諾數MHD方法.

盡管低磁雷諾數MHD方法,在高超聲速飛行領域得到了較為廣泛的應用和發展,但由于它采用了“忽略感應磁場”這一假設,其應用范圍受到限制.為了拓展低磁雷諾數MHD方法的應用范圍,本文針對“忽略感應磁場”這一核心假設,探討低磁雷諾數MHD方法在高超聲速領域適用性問題,分析全MHD方法在高超聲速流動領域局限性的產生原理,創建基于感應電流積分計算感應磁場對低磁雷諾數MHD方法進行修正的數值模擬方法.在此基礎上結合典型計算狀態,分析“忽略感應磁場”對計算結果的影響,探討低磁雷諾數方法的適用性問題.

2 低磁雷諾數MHD方法適用性分析

采用低磁雷諾數MHD方法,忽略了感應磁場的影響,必須滿足低磁雷諾數近似條件,即Rem≡μeσULp?1.這就對磁導率μe、電導率σ、速率U以及電磁流動相互作用區域Lp等多個方面的流體特征提出了要求,客觀上限制了低磁雷諾數MHD方法的應用范圍.

針對低磁雷諾數MHD方法的研究很多,但對于高超聲速流動適用的低磁雷諾數條件,目前仍存在一些爭議,尚未見到統一的結論.2002 年,Poggie和Gaitonde[21]開展了鈍體飛行器磁流體力學控制研究,認為Rem=3 時感應磁場可以忽略,可采用低磁雷諾數 MHD 方法;2007 年,Fujino 等[22]開展了再入飛行器磁控技術研究,認為Rem<1 時可采用低磁雷諾數MHD方法;Khan等[23]采用定電導率方法開展了磁場對邊界層速度分布影響的研究,探討了低磁雷諾數MHD方法的適用性,發現當Rem=2.5 時低磁雷諾數MHD方法基本失效,并給出了低磁雷諾數條件Rem<0.125 ,在此基礎上開展了二維鈍錐體Rem=0.179 時的磁流體數值模擬,發現采用低磁雷諾數MHD方法,對計算結果的影響小于 2.02%.2008 年,MacCormack[24]開展了強磁場下的磁流體力學控制數值模擬,認為Rem<1時可采用低磁雷諾數MHD方法,并開展了Rem=0.17 時磁流體加速裝置研究,發現采用低磁雷諾數MHD方法對軸線速度造成的計算偏差很小;同期,田正雨[1]基于國外的低磁雷諾數條件的研究,給出了較為保守的低磁雷諾數條件Rem<0.1;2009 年,Kim[25]對高超聲速流動的低磁雷諾數條件進行了探討,認為當氣體電離度小于1%時可應用低磁雷諾數MHD方法;2010年,Bocharov[26]綜合了Khan等[23]和MacCormack[24]等在低磁雷諾數MHD方法適用性方面的研究,給出低磁雷諾數條件Rem<0.5 ;2013 年,Fujino 和Ishikawa[8]開展了再入返回器大鈍體外形的磁流體數值模擬,計算狀態 64 km 時,磁雷諾數Rem=29.12 (Lp取鈍體尺寸 0.4 m),感應磁場最大僅相當于外加磁場的5.4%,采用低磁雷諾數MHD方法(忽略感應磁場)對流場結構和表面熱流的影響很小,其偏差基本可以忽略.

由于低磁雷諾數條件尚未達成一致性的結論,為了保證低磁雷諾數MHD方法的絕對適用,可選取最為保守的限制條件,即Rem<0.1.但對于高超聲速流動,由于其流速較高,很容易就接近或超出這一條件.例如,對于特征電導率 500 S/m、特征長度 1 m和特征速度 6 km/s的磁流體狀態,其特征磁雷諾數高達3.768.

事實上,國內外有很多研究在具體應用低雷諾數方法時,沒有嚴格討論其適用性問題.例如,2005年,Otsu[7]在開展鈍體磁流體數值模擬研究時采用低磁雷諾數MHD方法,其磁雷諾數Rem=3.26 (特征電導率取 400 S/m);2007 年,Yoshino等[27]在開展沿再入軌道的磁流體數值模擬時采用低磁雷諾數MHD方法,飛行高度75 km時磁雷諾數為 12.66.2012 年,Nagata 等[6]在開展鈍柱體磁流體力學控制阻力特性研究時采用低磁雷諾數MHD方法,其磁雷諾數Rem=2.04 (特征電導率取 250 S/m);2015 年,Takahashi等[9]在開展了火星探測器磁流體研究,經測算其磁雷諾數Rem高達196.9 (特征電導率取波后峰值電導率1600 S/m),數值模擬時仍采用低磁雷諾數MHD方法;2016年,國內學者在開展返回艙OREX磁控熱防護系統時采用低磁雷諾數MHD方法[28],經本文測算其數值模擬狀態的磁雷諾數Rem高達11.6.

造成這種現狀的主要原因可能包括兩個方面:

1)國外在開展低磁雷諾數條件探討時,一般通過對比低磁雷諾數MHD方法和全MHD方法.而全MHD方法在高超聲速領域的應用受到很大的限制,這將在某種程度上影響數值模擬的精準度.

全MHD方程組中的磁擴散方程包含磁擴散項νe?2B,其磁擴散率νe=1/(σμe) ,這里B為磁場磁感應強度.由于高超聲速流動的氣體磁導率μe、電導率σ一般較低,磁擴散率高,其磁擴散項大,甚至高出磁擴散方程中其他項幾個數量級,此時方程存在巨大的剛性,極大地影響了計算的穩定性和收斂性.尤其是高超聲速流場中很多區域氣體電導率接近于零,其磁擴散項趨近于無窮大,全MHD方程組幾乎無法直接求解,需要進行近似處理.

從物理的角度來看,電導率越小,磁場與流動的相互作用應該越弱,當電導率趨近于零時,高超聲速磁流體流動就退化為一般的高超聲速流動,使物理現象和問題得到簡化.此時全MHD方法反而出現數值模擬方面的困難,這在一定程度上反映了這種基于磁擴散方程的計算方法的局限性.

這種局限性產生機制,可結合全MHD方法的基本原理進行分析.由完整的磁流體力學控制基本方程[1,2]可知,在等離子體電磁流體相互作用過程中,電磁場對流場動量輸運F和能量輸運EM分別為:

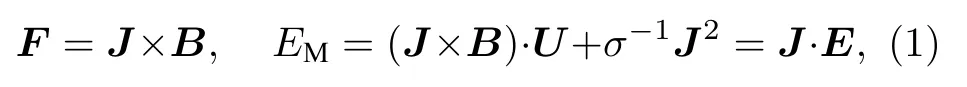
這里U為氣流速度.可見,電流J和電場E在電磁流體相互作用過程中,占據極其重要的地位,直接表征了電磁場對流動的干擾.而在全MHD方法中電流J和電場E由磁場的變化得到[4]:

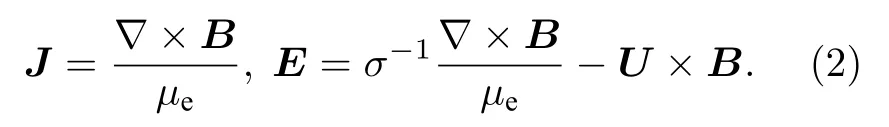
對于數值模擬來說,物理量偏導數的數值模擬精準度一般要低于物理量本身,例如熱流和摩擦阻力的計算精準度,一般就低于溫度和速度等參量的模擬精度,因此?×B的計算很容易出現數值誤差.而對于地球大氣,磁導率非常小μe≈4π×10?7h/m.當磁場B的一階偏導數由于某種原因(如數值誤差、迭代中間差量等)出現較小的非物理擾動時,該擾動反映在電流J和電場E上就會被放大106倍甚至更高.尤其是低電導率或零電導率時,電場E就面臨著“極小值除以極小值”甚至“零除以零”的極端情況.結合(1)式可以看出,這將直接影響電磁流動核心的動量與能量傳輸過程.可見,全MHD方法“以磁場的變化表征電場、電流變化”基本思路,在低磁導率、低電導率的高超聲速飛行領域存在缺陷,這將極大地影響計算的穩定性和有效性.

此外,由于磁擴散方程的數值解強烈依賴于磁場邊界條件,因此不恰當邊界條件可能帶來計算的準確性問題.求解經典麥克斯韋方程組,分界面上電磁場的連續性條件可寫為[29]:

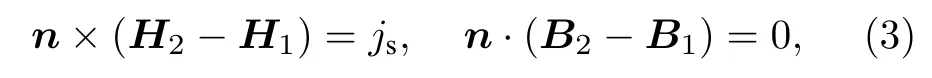
這里H2,H1分別為界面兩邊的磁場強度矢量,B2,B1分別為界面兩邊的磁感應強度矢量,js為界面電流密度,n為界面方向矢量.由于界面電流很難有效確定,真實的磁場交界面的切向分量很難直接給出.因此全MHD方法磁場氣固界面一般都采用近似條件[1?3]: 對于完全導體界面 dB/dn=0 ;對于絕緣壁面B=Bw.對比(3)式可知,這兩種邊界均不能完全涵蓋分界面電磁場的連續性條件.磁場邊界的不準確,將可能引入非物理的數值模擬誤差.

2005 年,MacCormack[30]采用全 MHD方法開展鈍體磁流體數值模擬,得到的結論是磁場使頭部區域 熱 流上升;2006 年,Khan 等[31]采用全MHD方法開展鈍體磁流體數值模擬,其中部分狀態磁雷諾數僅為0.01,此時感應(誘導)磁場遠小于外加磁場,但其計算結果與低磁雷諾數MHD方法結果存在明顯差異,這一計算結果的有效性也值得商榷;2009年,國內學者采用全MHD方法開展了RAM-C磁流體數值模擬[32],得到的結論同樣是磁場使頭部熱流上升.事實上,在飛行器頭部加載一定的磁場可以有效降低駐點熱流,這一點在試驗中已經得到了驗證.例如意大利航天中心開展了鈍體磁控熱防護試驗,磁場可使表面熱流下降46%[13,28].近兩年國防科技大學柳軍等開展了鈍體的磁控熱防護試驗研究,試驗結果也表明外加磁場能有效地降低端頭熱流.

由此可見,在探討低磁雷諾數條件時,全MHD方法在高超聲速領域的局限性,有可能會影響其定量結論的取得.

2)開展低磁雷諾數條件定量分析[12,23,24,30,31,33]時,氣體電導率計算多采用定電導率方法.

定電導率方法,即假定全流場的氣體電導率均為某一固定值,此時等離子體特征電導率及其作用區域的特征尺度較為確定,因此磁雷諾數提取相對簡單.而對于高超聲速流動,其混合氣體電導率與流動結構緊密相關.一般來說,僅激波后很小區域內氣體電導率相對較高,達到102—103S/m量級,其他流場絕大部分區域電導率均小于10 S/m,甚至接近于0.其等效等離子體特征電導率遠小于流場中峰值電導率,等效的等離子體特征厚度遠小于飛行器特征尺度(如球頭半徑等),且這兩者的直接提取相對困難.此時,如果采用流場中峰值電導率和飛行器特征尺度計算磁雷諾數,就會使計算得到的磁雷諾數遠遠大于真實的等效結果.

由此可見,低磁雷諾數MHD方法在低磁雷諾數條件的定量表征及其應用上,仍存在不確定性.對于具有低電導率特征的高超聲速磁流體模擬,選擇偏向保守的低磁雷諾數條件(Rem<0.1 )來判斷低磁雷諾數MHD方法是否適用,其必要性仍有待商榷.反之,如果完全忽視低磁雷諾數條件的限制,則有可能由于感應磁場不可忽略,引入較大的計算偏差.而常用的考慮“感應磁場”的全MHD方法在高超聲速領域存在較大的局限性,影響了計算的有效性.因此,有必要建立適用于高超聲速領域的考慮感應磁場的磁流體數值模擬方法.

3 修正方法的建立

由于低磁雷諾數MHD方法在流動控制方程方面沒作任何簡化,其形式與完整的磁流體力學方程組[1,2]中的流動方程一致.因此如果在低磁雷諾數MHD方法中,進一步考慮感應磁場的影響,那么這種方法就能從理論上突破低磁雷諾數條件的限制,在更大程度上反映完整磁流體力學方程的物理本質,因此適用范圍更加廣泛.

按照磁場矢量疊加原理,總的物理磁場可寫為

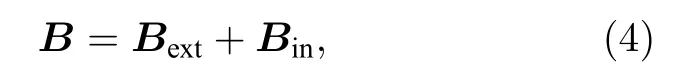
這里Bext為外加磁場,由機載磁場發生裝置產生;Bin為感應磁場(或稱誘導磁場),由等離子體中感應電流誘導產生.對于高超聲速磁流體力學控制來說,磁場對流場動量和能量的輸運需要時間的累積,因此其控制過程一般可近似為定常(或準定常)狀態.此時其收斂狀態的流場中感應電流J和感應磁場Bin的分布不隨(或近似不隨)時間變化,滿足(或近似滿足)電流穩恒和靜磁條件.因此r處的感應磁場Bin可由畢奧-薩伐爾定律積分給出:

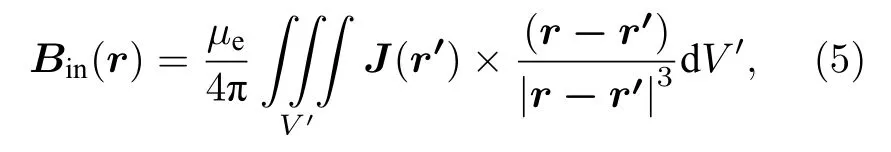
這里為r′和V′為體積積分的位置矢量和區間.

由畢奧-薩伐爾定律可直接推導出安培環路定理和磁場高斯定律[29],因此基于感應電流磁誘導積分得到的Bin,自動滿足了安培環路定理和磁場高斯定律.此時,按照磁場唯一性原理[29],這一Bin應與直接求解麥克斯韋方程中安培環路定理和磁場高斯定律等同,這從理論上說明了該方法的可行性.

基于畢奧-薩伐爾定律積分計算Bin,在省去了繁瑣的磁擴散方程或磁矢量勢泊松方程組離散與迭代求解過程的同時,還可以考慮邊界處可能存在的面電流影響(可將其直接列入積分),避免磁場邊界或磁矢量勢邊界難以確定的問題.因此其物理意義更加明確,計算更加簡便.

但這種方法也存在著明顯的缺陷.在感應磁場的每一步耦合迭代更新過程,對于流場中每一個流體微元都需要進行全場的感應電流的磁誘導積分.假設流場中N個微元,那么每一步迭代耦合的計算量將會達到N2量級.隨網格量增大,計算量將迅速增加.對于高超聲速復雜流動問題,計算網格很容易達到千萬(107)量級,此時計算量將高達1014量級,一般的計算機系統很難承受.

為了減小計算量和計算時間,必須對這種基于畢奧-薩伐爾定律直接積分的方法進行改進.這里由磁場高斯定律?·Bin=0 ,引入磁矢量勢Ain的概念:

然后由畢奧-薩伐爾定律給出磁矢量勢,(5)式變形可得:

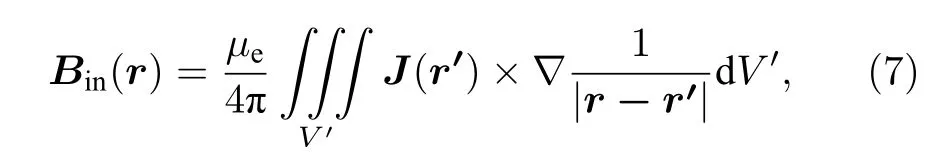
這里算符?是對r的微分算符,與r′無關,有恒等式:

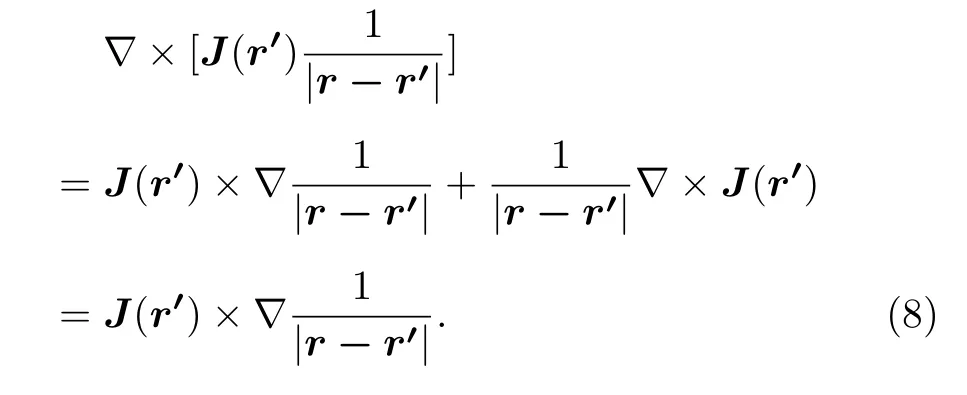
因此(7)式可寫為

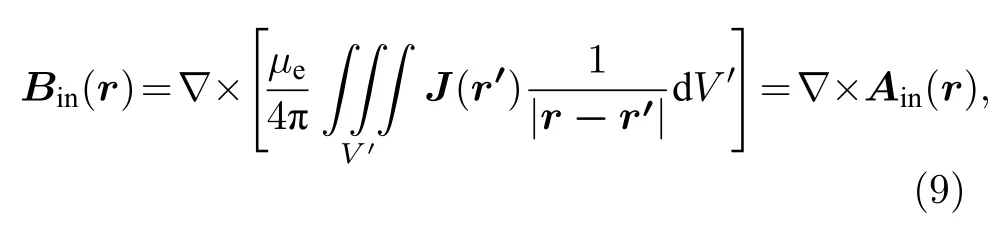
這里磁矢量勢Ain可寫為

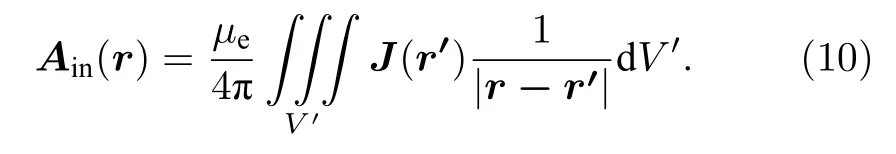
可見,只要基于感應電流積分計算式(10)式得到磁矢量勢,然后就可由(6)式得到感應磁場Bin分布.相比于(5)式,(10)式的積分計算要簡單得多,計算量也要小得多.

由于高超聲速磁流體力學控制磁場與流動相互作用的主要區域,相比于全流場空間的占比較小.因此,在計算感應磁場Bin時,可以根據磁流體流動特征對計算范圍進行縮減,進一步減小計算量.

1)縮減需要計算感應磁場Bin的區域

流場中并不是所有區域都需要計算感應磁場Bin,圖1(a)給出了文獻[34]計算的流場電導率,可以看出很大區域的電導率趨近于零.當流場某區域氣流的電導率很低甚至接近于零時,流體幾乎不受常規磁場的宏觀作用,此時該區域感應磁場存在與否,對流動干擾很小.換句話說,如果某區域的流體受常規磁場的影響很小,那么該區域的感應磁場可以不用計算.由于磁相互作用數可以在一定程度上表征磁場與流動耦合作用的整體效果,這里引入單位磁相互作用數Q′m的概念,令磁相互作用數中的特征磁感應強度和特征長度分別為1 T和1 m,即有=σ/ρu,這里ρ,u為氣體密度和速度大小.因此,需要計算感應磁場Bin的區域,可以通過氣體電導率或者單位磁相互作用數高于某個值進行判定:

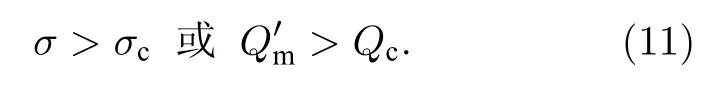
為了盡可能地覆蓋明顯影響磁流體力學控制的絕大部分區域,同時盡可能減少需要積分的計算區域,截斷電導率σc或者截斷單位磁相互作用數Qc應取值恰當.例如對于高超聲速流動,其激波后電導率為 102—103S/m,σc可取為 0.1—1.0 S/m或者更小.為了減小不同計算狀態的人為干預,這里引入截斷因子η:

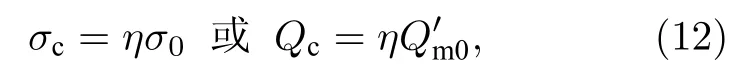
其中σ0為磁流體作用區域典型電導率,為磁流體作用區域典型單位磁相互作用數.在迭代初期,截斷因子η可選用較大的值,如η=10?1—10?3,以減小計算量,加快收斂;在迭代后期,η可選用較小的值,如η=10?4—10?6,以提高計算精度.

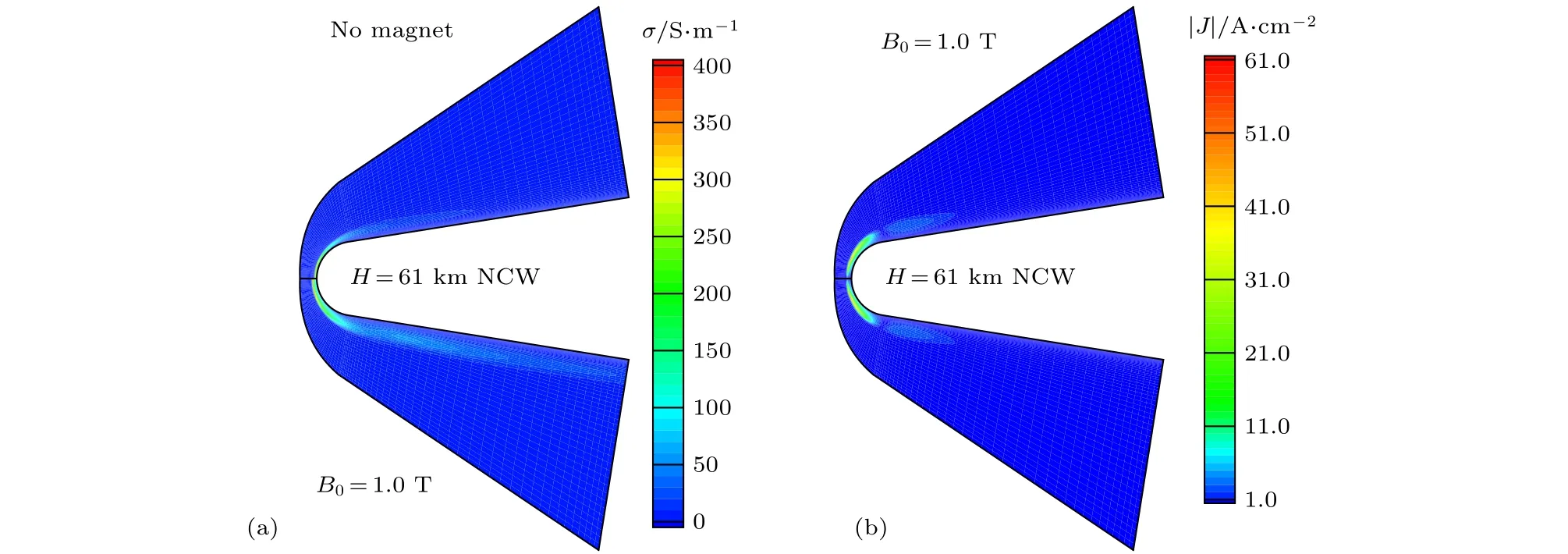
圖1 流場中電導率和環形感應電流分布[34] (a)電導率;(b) 電流密度Fig.1.Distribution of electronic conductivity and annular electric current: (a) Conductivity;(b) current.

2)縮減計算某一點感應磁場Bin所需要的感應電流積分區域

流場中某一點的感應磁場,由全場每個微元電流在該點產生的感應磁場疊加得到.由圖1(b)可以看出,高超聲速流場中感應電流主要集中于流場與電磁場相互作用的小部分區域,很大區域電流趨近于零.因此,也可以引入類似于(11)式和(12)式的條件,來判別計算感應磁場Bin時需要積分的空間區域:

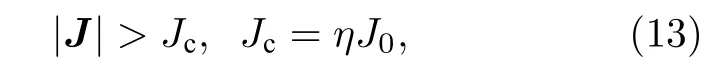
這里Jc為截斷電流密度大小,J0為磁相互作用區典型電流密度.

3)縮減相互作用區間

此外由(5)式還可以看出,由電流微元產生的感應磁場與距離的平方呈反比關系.可見由穩恒(或近似穩恒)的感應電流產生的磁場,其主要作用區域應該為有限的空間,將其定為

這里Lc為磁流體作用區域的特征尺度;L為感應磁場作用區間尺度,超出L流場空間,不參與該外加磁場作用區域的感應磁場計算;λ為放大因子,可結合具體的物理實際進行設置,本文數值模擬時λ=5.

4)耦合策略

由于流動收斂的速度遠遠小于感應電流生成誘導磁場的響應速度,因此在實際的數值模擬過程中,先采用不考慮感應磁場的低磁雷諾數MHD方法迭代計算直至結果基本收斂,然后每隔500—5000步進行一次感應磁場修正,迭代計算直至結果重新收斂.

4 數值計算分析

4.1 無限長直流導線產生磁場

為了保證電流數值離散積分過程的正確性,首先對電流積分計算磁場的程序模塊進行校驗,這是本文低磁雷諾數MHD方法修正的基礎.

對于通電電流為I的無限長直導線,導線外距離為r的任意一點的磁場B由安培環路定理計算:

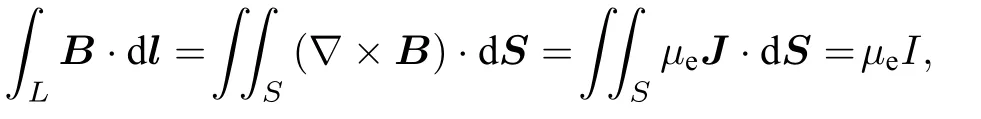
這里L為半徑為r的圓周,S為圓面,圓面方向為電流方向.由于對稱性因此有磁感應強度大小B=μeI/2πr,其方向符合右手系.

采用半徑為1 mm的直導線,電流I=1.0A.假設電流在導線截面內均勻分布,則電流密度約為J=3.18×105A/m2,這與圖1(b)流場感應電流密度在同一數量級.為了保證“無限長”的假設近似成立,本文取直導線長為100 m.采用圓柱形網格,網格點設為 1 0001×51×181 ,沿導線長方向的網格點均勻分布,其他兩個方向非均勻分布.

圖2給出了不同位置的磁場感應強度與理論值的比較.由圖2(a)可以看出,在導線的端頭(x=0.0 m)附近,數值積分的磁感應強度明顯小于理論值,這是因為x<0.0m 的部分被人為截斷,沒有參與數值積分,因此不滿足“近似無限長條件”.隨著x增大,這種“人為截斷”產生影響逐漸減小,數值結果逐漸趨近于理論值,長直導線中點 (x=50.0 m),數值結果幾乎與理論值完全重合.圖2(b)中也有類似的現象: 當r較小時,數值結果與理論值幾乎完全重合,隨r進一步增大,r逐漸接近甚至大于導線的長度,此時“人為截斷”產生的影響逐漸增大,不再滿足“近似無限長條件”,數值結果與理論值偏離.

由此可見,數值積分計算結果符合理論預期.這說明本文基于電流積分的磁場計算程序模塊能較為準確地給出空間磁場分布,滿足感應磁場計算精度要求.

4.2 三維鈍柱體外形考慮感應磁場修正的磁流體數值模擬

為了進一步校驗本文修正計算方法的有效性,開展鈍柱體外形高超聲速磁流體數值模擬,該算例有低磁雷諾數方法和全MHD方法計算結果[33].計算外形頭部半徑 0.01 m,柱體長 0.075 m.計算來流為混合電離氣體,來流溫度 9000.0 K,來流壓力7726.0 Pa,來 流 密 度 0.01429 kg/m3,來 流 速 度6710.0 m/s,壁面溫度 12000.0 K.采用偶極子磁場,磁場中心位于頭部球心,磁特征感應強度B0=4.0T,磁場特征長度為 0.01 m.采用固定電導率方法,全場混合氣體電導率均為 4800 S/m,特征磁相互作用數為69.

圖3和圖4分別給出了本文計算的外加磁場和感應磁場分布,并與文獻[33]給出的結果進行對比,圖中數值乘以轉化為以特斯拉為單位的量.由圖可以看出,本文修正方法計算得到的感應磁場,相對于外加磁場量值較小;除局部細節外,整體分布變化規律和量值均與全MHD方法的結果[33]相符合,這說明本文修正方法能較好計算磁流體流動過程中的感應磁場分布.

為了進一步分析感應磁場細節差異產生的原因,圖5給出了不同計算方法得到的流場壓力分布.可以看出,在磁場作用下本文計算得到的流場壓力分布規律與文獻[33]基本一致,但本文給出的激波脫體距離明顯大于文獻結果.這是由于文獻[33]沒有給出混合電離氣體的成分,也沒有明確氣體狀態計算方法,而本文采用的等效比熱比的氣體計算方法,可能與文獻[33]中的氣體模型不一致.事實上,文獻[33]給出的該狀態磁場使激波脫體距離增大的倍數并不確定,為 3—7.5倍[33],圖2—圖5中文獻結果為增大3倍的結果,而本文計算結果為磁場使激波脫體距離增大約4—5倍.本文計算激波脫體距離較遠,導致了感應磁場分布細節上的差異.

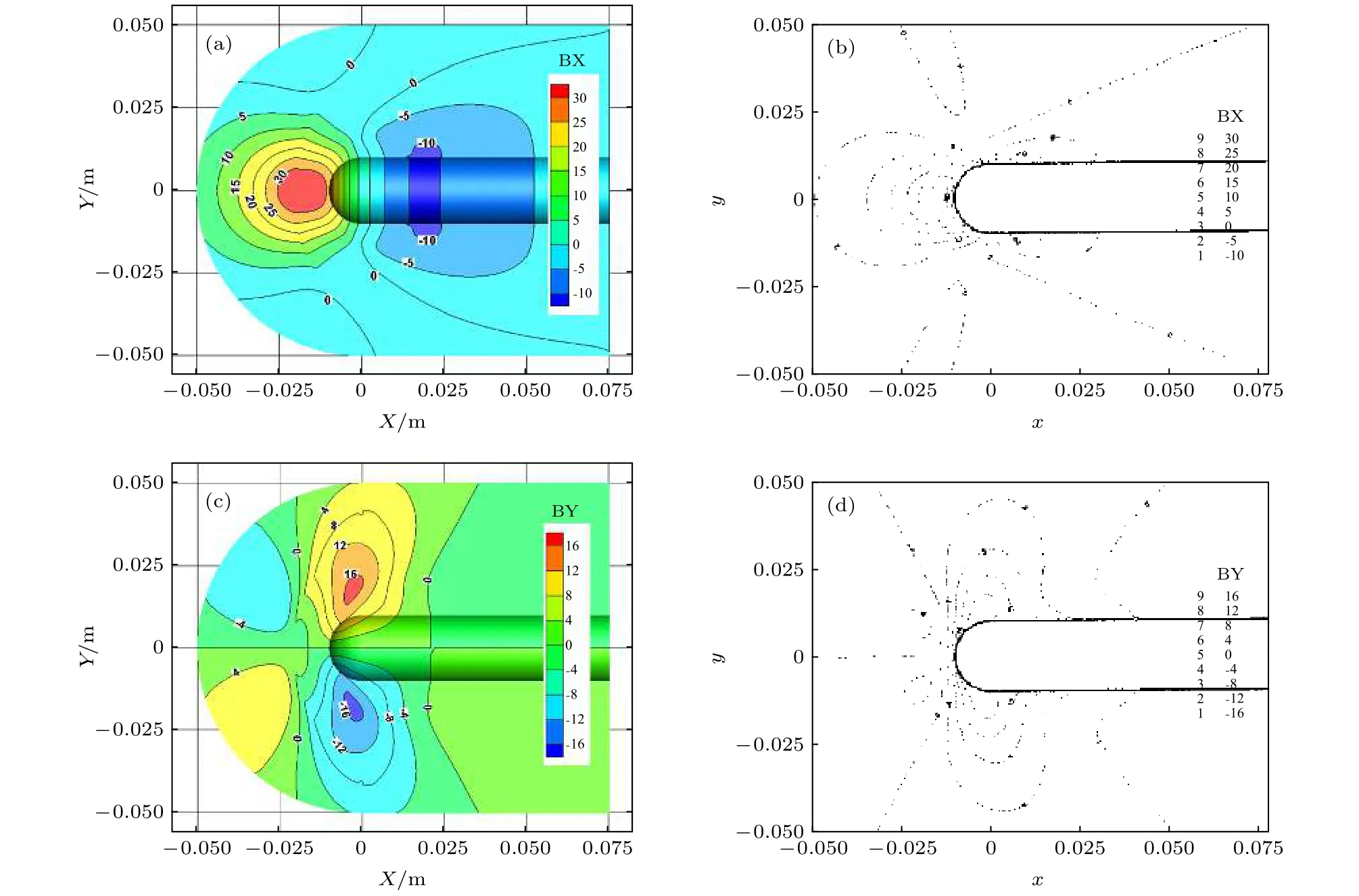
圖4 感應磁場 (a)本文 BX;(b)文獻 BX;(c)本文 BY;(d)文獻 BYFig.4.Induced magnetic field: (a) BX of this paper;(b) BX[33];(c) BY of this paper;(d) BY[33].

由圖5還可以看出,本文修正方法計算得到的壓力與一般的低磁雷諾數MHD方法模擬結果,除局部細節外的分布規律基本一致,與文獻[33]“低磁雷諾數MHD方法和全MHD方法結果之間的差異”類似.這里以磁場尺度和來流速度為特征量,計算磁雷諾數Rem≈0.4.可見,此時采用低磁雷諾數假設忽略感應磁場,對流場結構的影響不大,這與圖3和圖4顯示的“感應磁場相對于外加磁場的量值較小”相互印證.

4.3 Ram-C鈍錐“忽略感應磁場”對磁流體數值模擬影響的分析

文獻[35]為了分析電導率模擬準確性問題,基于低磁雷諾數方法探討了國內外常見的多種電導率模型差異及其影響,其中采用電導率模型M6 時,流場中峰值電導率高達 6000 S/m,其磁雷諾數遠高于0.1,低磁雷諾數方法的適用性有待商榷.本文結合這一典型飛行狀態與計算條件,開展一般低磁雷諾數方法和本文修正方法的數值對比計算,分析“忽略感應磁場”對磁流體控制數值模擬的影響,探討低磁雷諾數條件適用性.

采用RAM-C鈍錐體外形[35,36],計算飛行高度 71 km,飛行速度 7650 m/s,等溫壁面條件,壁面溫度 1500 K,完全非催化壁面條件.磁場配置采用磁偶極子磁場,磁感應特征強度B0=0.5T ,特征長度r0=0.1524 m,磁偶極子方向為直角坐標橫軸負方向.采用電導率模型M6[35],其形式為σ=1.56×10?2T1.5/ln(1.23×107T1.5/n0e.5),T為溫度,ne為電子數密度.采用11組分Park反應模型計算等離子體分布.

圖6給出了采用M6模型計算得到的流場中電導率分布,圖6(a)為采用一般低磁雷諾數MHD方法模擬得到的流場電導率分布云圖,圖6(b)為采用修正方法和一般低磁雷諾數MHD方法計算得到的駐點線電導率分布比較.可以看出,在磁場作用下流場峰值電導率可達5000 S/m,但取得峰值電導率的等離子區域厚度較薄,波后較大區域內氣體電導率僅為1000 S/m左右.采用不同方法計算,磁場對激波脫體距離的外推效果存在差別,采用修正方法得到的激波脫體距離,比采用一般低磁雷諾數MHD方法結果稍小.

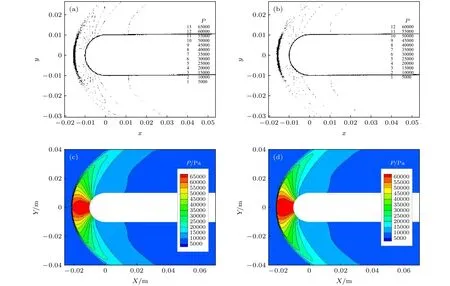
圖5 不同方法計算的流場壓力分布 (a)文獻低磁雷諾數MHD方法;(b)文獻全MHD方法;(c)本文低磁雷諾數MHD方法;(b)本文修正方法Fig.5.Distribution of pressure in the flow computed by different method: (a) Low Rem method[33];(b) full MHD method[33];(c) low Rem method of this paper;(d)improved method of this paper.

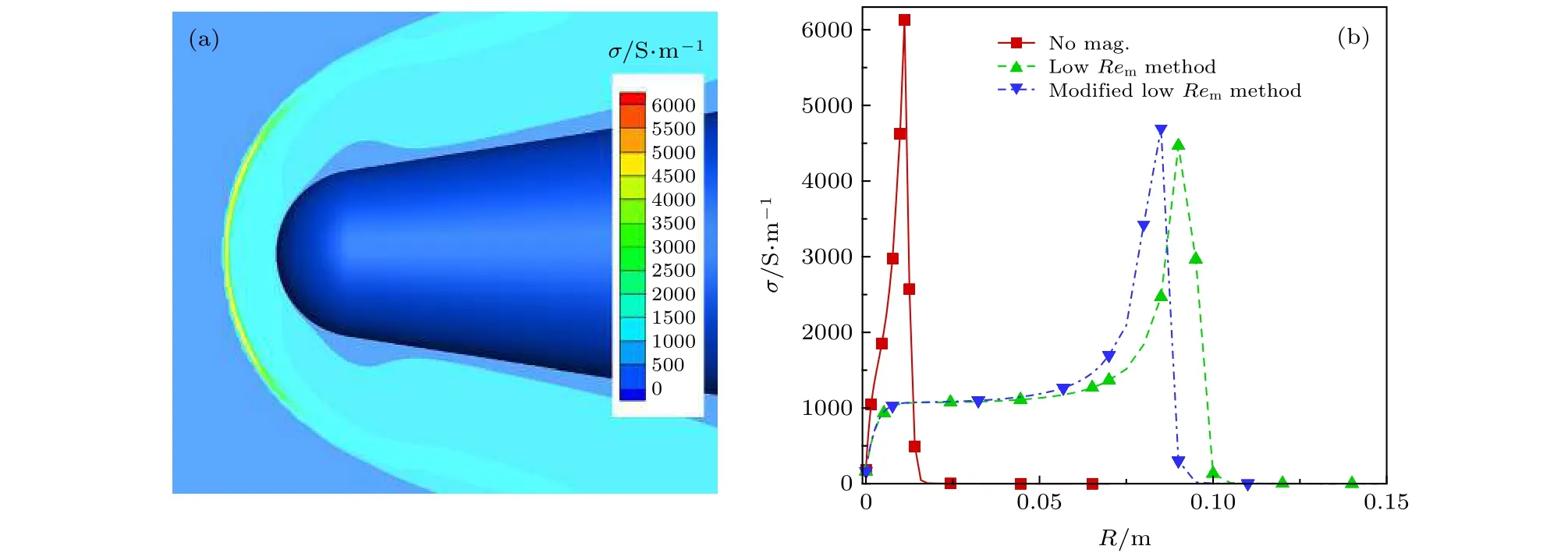
圖6 采用電導率模型M6計算的流場電導率分布 (a)全場云圖;(b)駐點線參數分布Fig.6.Distribution of electronic conductivity using M6: (a) Full contour map;(b) parameters along stagnation line.

圖7給出了修正方法計算得到的感應磁場分布.對比圖4可以看出,感應磁場的整體分布與4.2節鈍柱體的感應磁場分布大體相似,但二者又有明顯的差異.造成差異的原因可能有兩個方面:一是計算外形差別;二是電導率分布存在差別,尤其是激波波前位置,4.2節采用定電導率方法,其流場波前氣體電導率為4800 S/m,此時波前流動也會產生較強的環形感應電流;而本節狀態的流場波前電導率接近于零,波前環形電流也接近于零.這種感應電流分布的差異必然影響感應磁場的分布.

為了衡量感應磁場的相對大小,圖8進一步給出了外加磁場分布和全磁場分布,這里全磁場是外加磁場與感應磁場疊加的結果.結合圖7可以看出,除局部細節外,感應磁場方向大體上與外加磁場相反,感應磁場的影響在某種程度上相當于對外加磁場作用效果的削弱.這是符合磁電阻擴散基本原理的,由楞次定律可知,具有導電性的等離子體在磁場中運動時,其感應磁場方向總是對抗磁通量的變化方向,因此整體上表現為對原磁場的某種削弱,整體影響幅度不大,其x分量最大值相當于外加磁場x方向最大值的7.9%左右,其y分量最大值相當于外加磁場y方向最大值的4.6%左右.

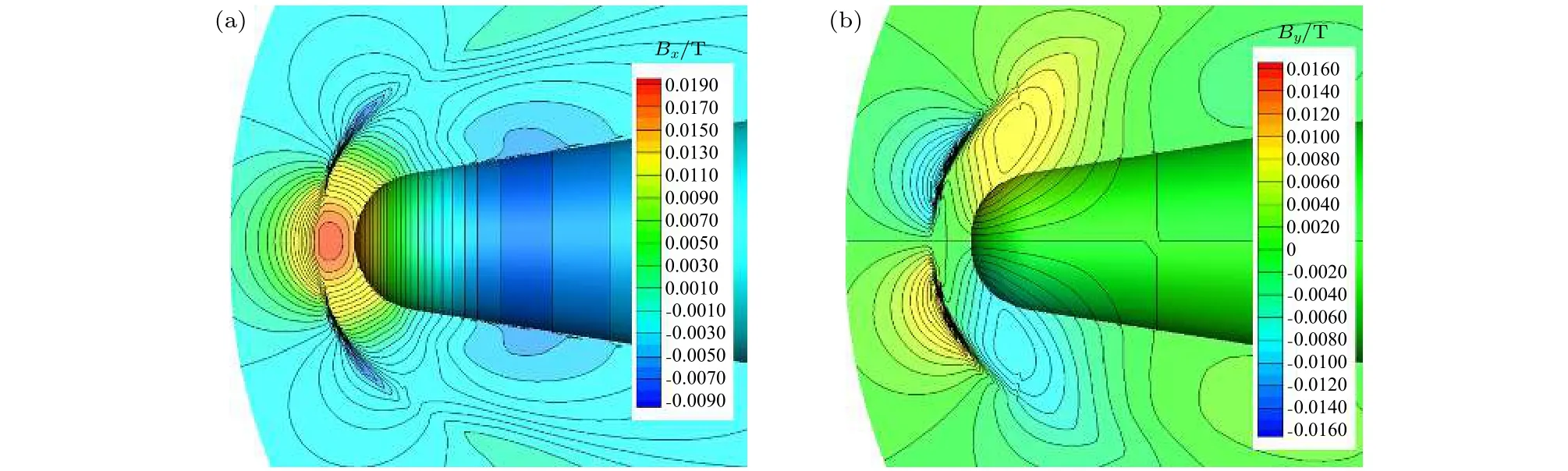
圖7 修正方法計算的鈍錐 RAM-C 感應磁場 (a) Bx 分量;(b) By 分量Fig.7.Induced magnetic field of RAM-C using improved method: (a) Component Bx ;(b) component By.

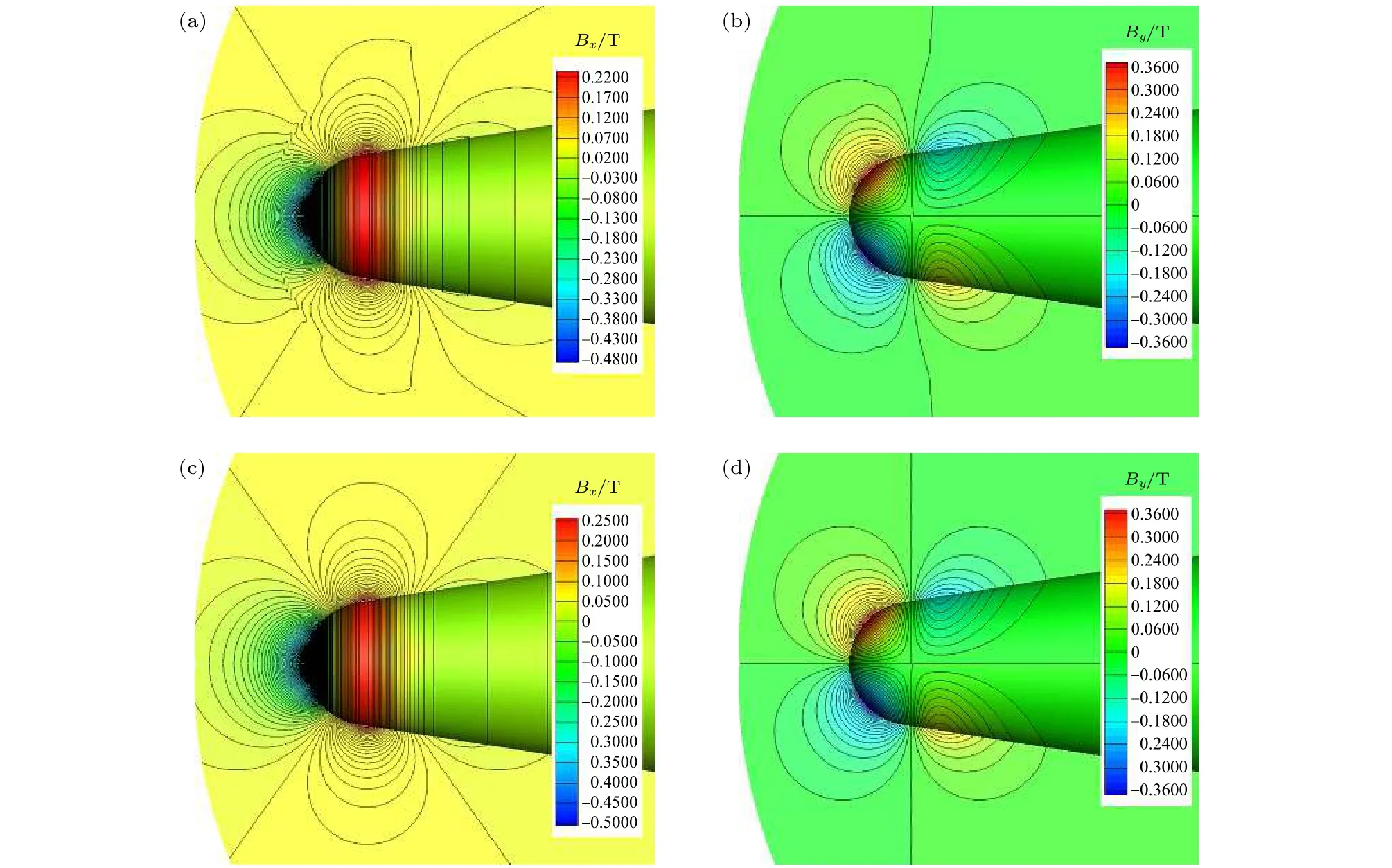
圖8 鈍錐 RAM-C 外加磁場和修正方法計算的全磁場分布 (a)全磁場 Bx 分量;(b)全磁場 By 分量;(c)外加磁場 Bx 分量;(b) 外加磁場 By 分量Fig.8.Total magnetic field computed using improved method and externally applied magnetic field of RAM-C: (a) Total Bx ;(b) total By ;(c) externally Bx ;(c) externally By.

表1給出了不同條件或方法計算得到的阻力系數,可以看出,采用修正方法計算得到的阻力系數與一般低磁雷諾數MHD方法計算結果的差異在1%左右,其磁控效果沒有本質差別.

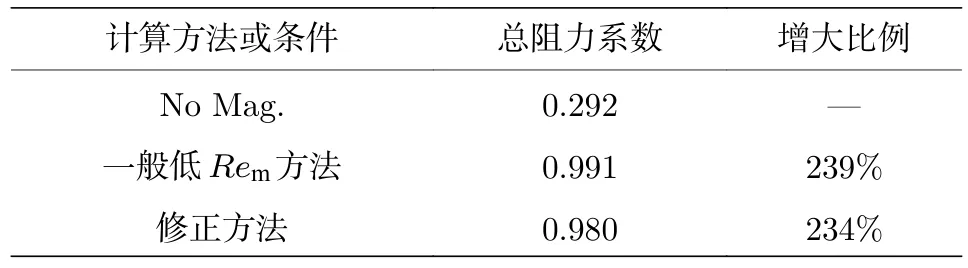
表1 鈍錐 RAM-C 阻力系數Table 1.Drag coefficient of RAM-C.

圖9進一步給出了不同計算方法得到的表面熱流分布.由圖可以看出,采用修正方法計算得到的熱流與采用一般低磁雷諾數MHD方法的結果局部存在差異,但整體分布趨于一致,這說明磁控熱防護效果沒有本質差異.在X=0 m 附近,兩者差異稍大,采用修正方法的熱流的磁控熱防護效率比一般低磁雷諾數MHD方法的下降不到10%.可見,考慮感應磁場影響在一定程度上降低了局部區域的磁控熱防護效果.

圖9 修正方法和一般低磁雷諾數MHD方法計算得到的熱流分布比較Fig.9.Heat flux computed using Low Rem method or improvbed method.

這里結合磁雷諾數進行分析,按傳統的低磁雷諾數的計算方法,以流場中峰值電導率、磁場特征尺度和氣體來流流速為特征量,則磁雷諾數Rem≈7.3,此時不符合低磁雷諾數條件要求.如果以波后較大區域電導率1000 S/m和頭部等離子體層厚度0.1 m為特征量,則磁雷諾數Rem≈0.96.兩者差異較大,后者綜合考慮了等離子體的實際分布特征、磁擴散方向以及電磁相互作用區間,因而更加準確,但其結果仍然比保守的低磁雷諾數條件(Rem?0.1 )高得多.結合圖8和表1 “忽略感應磁場對計算結果影響較小”的結論可以看出,對于本文這種不含人工電離的高超聲速空氣流場計算狀態,“Rem<0.1 ”的低磁雷諾數條件過于保守,可擴展為Rem<1.0 ,同時其特征電導率和特征尺度應綜合考慮實際的等離子體分布.

圖10進一步給出兩種修正方法計算得到的熱流和殘差收斂曲線.Modified Method 1 為直接積分計算畢奧-薩伐爾定律積分的方法,Modified Method 2為基于電流積分計算磁矢量勢同時考慮截斷因子對計算區域進行縮減的方法.由圖可以看出,這兩種方法計算得到的熱流幾乎完全重合,計算精度相當.本文 Modified Method 2 的計算時間較短,效率較高.

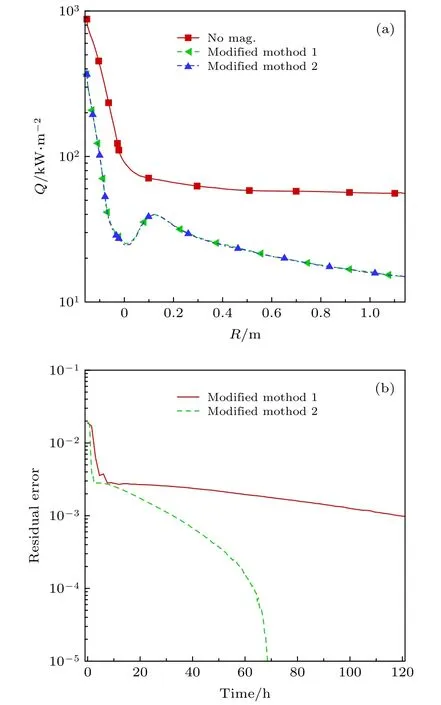
圖10 采用不同修正方法計算得到的熱流和殘差收斂曲線 (a)熱流;(b)殘差Fig.10.Heat flux and residual error computed using different modified method: (a) Heat flux;(b) residual error.

5 結 論

(1)本文在詳細探討低磁雷諾數方法適用性以及全MHD方法局限性及其原理的基礎上,基于感應電流積分計算磁矢量勢得到感應磁場,提出了一種低磁雷諾數MHD修正計算方法,突破了“低磁雷諾數假設”的限制,增強了低磁雷諾數MHD方法的適用性,拓寬了應用范圍.考核驗算表明,該方法可較為準確地計算模擬磁流體流動中的感應磁場,數值模擬結果與理論分析及文獻結果相符,具有較高的可信度.

(2)針對典型計算狀態,開展了常規低磁雷諾數MHD方法和修正方法的數值對比計算,探討了感應磁場對磁流體力學控制數值模擬的影響,分析了采用常規低磁雷諾數MHD方法在流場特性、氣動力/熱特性等方面造成的計算偏差.研究結果表明: 1)高超聲速流動過程中感應磁場的影響在宏觀上表現為對外加磁場的削弱和扭曲,一定程度上降低了磁控效果;2)文獻[35]采用常規的低磁雷諾數MHD方法“忽略感應磁場”造成的計算偏差,對其計算結論的取得不構成實質性影響;3)相比于全域直接積分計算畢奧-薩劃爾定律,本文基于電流積分計算磁矢量勢同時考慮截斷因子對計算區域進行縮減的耦合計算方法,在計算時間和效率方面具有明顯優勢;4)本文計算條件下,“Rem<0.1”的低磁雷諾數條件過于保守,建議取為Rem<1.0,同時其特征電導率和特征尺度應綜合考慮實際的等離子體分布.