基于季節(jié)分解和SARIMA-GARCH模型的鐵路月度客運量預測方法

錢名軍，李引珍,阿茹娜

(1.蘭州交通大學 交通運輸學院，甘肅 蘭州 730070； 2.中國中鐵股份有限公司 規(guī)劃發(fā)展部， 北京 100039)

鐵路客運系統(tǒng)作為一個與外界頻繁進行能量、信息交換的典型的開放、動態(tài)、非線性復雜巨系統(tǒng)，其客運量時間序列是該系統(tǒng)運轉所產生的外在表現數據。它蘊含了旅客運輸過程中的大量信息，是各種因素對鐵路客流綜合作用的結果，呈現出復雜的變化趨勢和波動特性。因此，有必要深入研究鐵路客運量時間序列，從中提取并利用有關規(guī)律信息，為鐵路客運部門靈活制定列車開行計劃、合理配置和運用客車車底，提高客運服務質量乃至科學制定路網規(guī)劃建設方案等提供決策參考。

當前，對客運量時間序列的預測研究，主要運用神經網絡[1-2]、機器學習[3-5]、混沌理論[6]、ARIMA(Auto-Regressive Integrated Moving Average)模型[7-8]、灰色理論[9]、馬爾科夫模型[9-10]或卡爾曼濾波等技術方法來提高對數據的擬合精度。文獻[1]提出了消除高鐵節(jié)假日影響的數據替補修正法和融合變分模態(tài)分解(VMD)、遺傳算法(GA)及BP神經網絡的VMD-GA-BP客運量預測法。文獻[3]提出一種基于深度學習與神經網絡相結合的小時客流預測模型SAE-DNN，并將其應用于廈門市BRT公交站的客流預測。文獻[6]將相空間重構方法用于對與鐵路運量相關的時間序列進行混沌特性識別，并采用最大Lyapunov指數預測方法對鐵路客貨運量進行預測分析。文獻[7]針對移動假日對鐵路客運量的雙峰影響，采用X-12-ARIMA季節(jié)調整模型，建立鐵路客運量的三時段春節(jié)季節(jié)調整模型，取得了較好效果。文獻[8]針對北京地鐵進站客流呈現以“周”為周期的波動規(guī)律，采用了SARIMA季節(jié)時間序列模型進行預測。文獻[10]將指數平滑法與馬爾科夫模型綜合用于公路客運量預測。可見，現有客運量預測研究或側重于對宏觀的年度增減趨勢進行預測，或側重于對相對微觀的節(jié)假日、周、日客運量進行預測，而對中觀層面的月度或季度客運量變化規(guī)律及特點的研究不夠深入。

伴隨經濟和社會的快速發(fā)展，人們的出行需求更加多元化、動態(tài)化，為及時響應旅客需求的快速變化以適應客運市場的激烈競爭，鐵路客運組織計劃在保持運能與運需基本均衡的前提下需具備一定的靈活性。而目前鐵路部門在制定旅客運輸計劃時大多參照年度客流數據進行決策，對月度或季度客流所反映出來的短期波動變化響應不夠及時。年度客流數據雖然能較好地反映鐵路客運市場中長期的變化趨勢，但時間跨度仍然較大，在一定程度上掩蓋了一年中不同月份客運量的季節(jié)性、周期性和隨機波動性，不利于客運組織部門及時靈活地調整旅客列車開行計劃、機車車輛運用計劃等以適應月度客運市場的相應變化。

實際上，鐵路月度或季度客運量在受鐵路自身運能影響的同時，還與近期國民經濟發(fā)展狀態(tài)、季節(jié)氣候以及其他交通方式的相互作用有關，具有明顯的中長期變化趨勢性和周期性；同時又因移動節(jié)假日效應或突發(fā)重大事件的存在，而具有顯著的隨機波動性。因此，對月度客運量變化規(guī)律進行研究具有重要的現實意義。文獻[11]針對鐵路月度客運量序列中存在的趨勢成分和季節(jié)成分構建出SARIMA(2,1,1)(0,1,0)12模型，其預測精度較Excel趨勢線法、XGBOOST算法略有提高，但預測效果仍不算理想。主要原因在于，該SARIMA模型定階不夠準確，且關鍵是對序列中存在的非線性波動成分(即ARCH異方差效應)未予以考慮并進行有效提取。

基于此，本文以鐵路月度客運量時間序列為研究對象，首先，對其趨勢性、季節(jié)性和隨機性進行季節(jié)分解，并通過季節(jié)、非季節(jié)差分序列的相關圖識別篩選出擬合優(yōu)度更高的SARIMA基礎模型。然后，為消除異方差、提高模型預測精度，再對SARIMA基礎模型的回歸殘差進行GARCH效應建模，得到SARIMA(2,1,1)(1,1,1)12-GARCH(1,1)融合模型。最后，對融合模型的穩(wěn)定性及預測性能進行檢驗、分析。

1 SARIMA-GARCH融合預測方法

研究表明，鐵路月度客運量時間序列具有非平穩(wěn)、非線性、周期性以及存在異方差性，為此將SARIMA模型與GARCH模型進行融合建模[12-13]，以提高預測精度。

1.1 季節(jié)時間序列模型SARIMA

SARIMA從自回歸差分移動平均模型ARIMA衍生而來[7]。該模型通過對非平穩(wěn)時間序列進行差分轉化為平穩(wěn)時間序列后，將因變量僅對它的滯后項及隨機誤差項的現值和滯后值進行回歸來構建模型，很適合非平穩(wěn)單變量時間序列的預測。

若某時間序列經s個時間間隔后觀測值呈現出相似性，如同時出現波峰或波谷狀態(tài)，則稱該序列是以s為周期的季節(jié)時間序列。令周期為s的非平穩(wěn)季節(jié)時間序列(包括日、周、月或季度序列)為{Yt}(t為時間序列樣本長度)，則其經d階非季節(jié)差分、p階自回歸、q階移動平均的ARIMA(p,d,q)模型為

ΔdYt=c+α1ΔdYt-1+α2ΔdYt-2+…+

αpΔdYt-p+ut+β1ut-1+β2ut-2+…+βqut-q

(1)

式中：c為常數項；α1,α2,…,αp為自回歸系數；β1,β2,…,βq為移動平均系數；ut為隨機擾動項。

式(1)右邊前半部分為自回歸過程，后半部分為移動平均過程。

顯然，式(1)等價于

ΔdYt-α1ΔdYt-1-α2ΔdYt-2-…-αpΔdYt-p=

c+ut+β1ut-1+β2ut-2+…+βqut-q

(2)

引入滯后算子L，可以得到

LΔdYt=ΔdYt-1

LnΔdYt=ΔdYt-n

式中：n為任意正整數。

特別地L0ΔdYt=ΔdYt。

則式(2)可寫為

(1-α1L-α2L2-…-αpLp)ΔdYt=

c+(1+β1L+β2L2+…+βqLq)ut

(3)

令平穩(wěn)的自回歸算子

Φp(L)=1-α1L-α2L2-…-αpLp

可逆的移動平均算子

Θq(L)=1+β1L+β2L2+…+βqLq

代入式(3)即得ARIMA(p,d,q)簡式

Φp(L)ΔdYt=c+Θq(L)ut

(4)

同時，定義季節(jié)差分算子Δs=1-Ls，則一次季節(jié)差分表示為

ΔsYt=(1-Ls)Yt=Yt-LsYt=Yt-Yt-s

(5)

對于非平穩(wěn)季節(jié)性時間序列，需經D階季節(jié)差分來消除季節(jié)性影響，才可建立周期為s的P階自回歸、Q階移動平均季節(jié)時間序列模型

(6)

式中：AP(Ls)、BQ(Ls)分別為非平穩(wěn)季節(jié)時間序列的自回歸算子與移動平均算子。

當式(6)的隨機擾動項ut非平穩(wěn)且存在自回歸(Auto-Regressive, AR)或移動平均(Moving Average, MA)成分時，再對ut建立ARIMA(p,d,q)模型

Φp(L)Δdut=Θq(L)vt

(7)

式中：vt為白噪聲。

把式(7)代入式(6)，即得SARIMA(p,d,q)×(P,D,Q)s模型

(8)

顯然，當P=D=Q=0時，SARIMA(p,d,q)×(P,D,Q)s模型退化為ARIMA(p,d,q)模型，因此說ARIMA是SARIMA的特例。當p=d=q=P=D=Q=0時，SARIMA模型退化為白噪聲模型。

1.2 廣義自回歸條件異方差模型GARCH

通常，非平穩(wěn)時間序列模型的方差不僅隨時間變化，而且有時變化劇烈，表現出“波動集聚(Volatility Clustering)”特征，即方差在一些時段比較小，而在另一些時段會比較大。這種現象就說明模型殘差存在異方差效應(ARCH)。當存在ARCH效應時，有必要對異方差進行正確處理以使回歸參數的估計量更具顯著性，避免異方差對時序模型產生不良影響，從而提高模型的預測精度。GARCH模型可以用于對解釋變量的方差建模，以提高均值方程參數估計的有效性。

GARCH(p,q)由ARCH(q)模型擴展而來[14]。ARCH(q)模型由諾貝爾經濟學獎獲得者恩格爾提出，它針對均值方程的殘差波動項建立模型并用于預測，模型表達式為

均值方程：

Yt=F(t,Yt-1,Yt-2，…)+ut

(9)

式中：F(t,Yt-1,Yt-2…)為時間序列{Yt}的確定信息擬合模型，本文為所建SARIMA(p,d,q)×(P,D,Q)s模型。

條件方差方程為

(10)

式中：It-1為已知信息集；ω0為常數項。

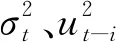
(11)

式中：ω為ARCH項參數；θ為GARCH項參數。

綜上，GARCH模型考慮了異方差效應對時序模型的影響，能對因變量的方差進行更準確的預測，因此可以提高均值方程參數估計的有效性，改善時序模型的預測精度。

2 鐵路月度客運量時間序列特征分析

本文從國家統(tǒng)計局官網提取到2005年1月—2019年5月年共173組鐵路月度客運量統(tǒng)計數據，構成時間序列研究樣本。

2.1 月度時間序列的平穩(wěn)性檢驗

由圖1可知，鐵路月度客運量序列與時間呈指數關系，非線性、非平穩(wěn)性和趨勢性顯著，且存在遞增型異方差，直接建模難以取得良好效果。所以，建模前先對原始序列Y取自然對數得LY序列(異方差得到一定程度抑制，見圖2)，再對LY序列進行平穩(wěn)化處理和單整性檢驗。

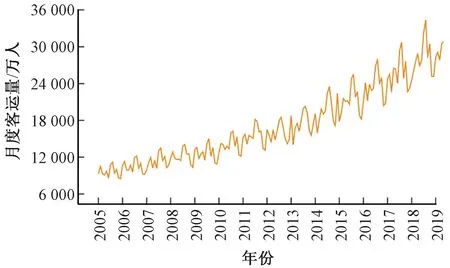
圖1 客運量原始序列Y的時序圖

本文采用ADF單位根檢驗法來判定時間序列的平穩(wěn)性。若不平穩(wěn)，則對LY序列依次進行d階差分直至序列平穩(wěn)，再進行分析建模。對LY序列的平穩(wěn)性ADF檢驗結果見表1。

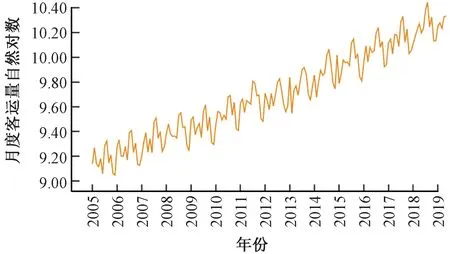
圖2 客運量對數序列LY的時序圖

表1 LY序列ADF檢驗結果

檢驗結果分析：(1)LY序列的ADF檢驗統(tǒng)計量均大于1%、5%和10%水平的臨界值，且接受存在單位根的原假設的概率為0.348 8。所以，LY序列是非平穩(wěn)序列。(2)經一階差分后的序列ΔLY對應的ADF檢驗統(tǒng)計量為-20.246 6，小于1%的顯著水平臨界值，其接受存在單位根原假設的概率為0，即不接受原假設，表明ΔLY是平穩(wěn)的。同時，從一階差分序列ΔLY的時序圖3也可看出，差分序列圍繞0軸上下波動，呈現出良好的平穩(wěn)性。綜上，LY序列為一階單整序列，記為LY～I(1)。

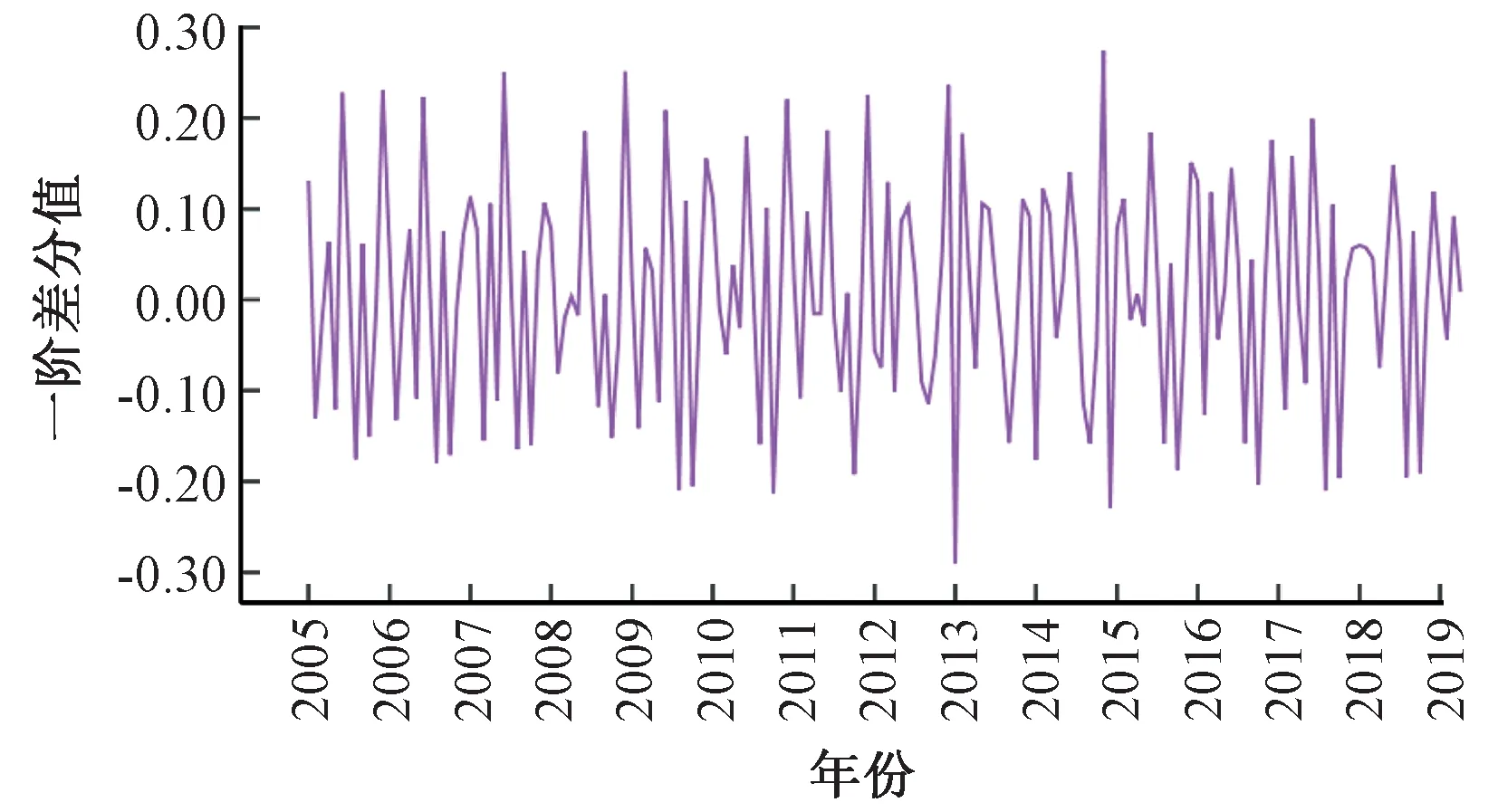
圖3 一階差分序列ΔLY的時序圖

2.2 月度客運量時間序列特征信息分解

為了直觀準確表征趨勢因素、季節(jié)因素和隨機因素的存在，本文根據鐵路月度客運量序列具有遞增型異方差特性，采用季節(jié)分解的乘法模型，把{Yt}分解為趨勢循環(huán)分量Tt、季節(jié)分量St和隨機分量It：Yt=Tt×St×It。

具體分解步驟有如下3個階段[15]：

第一階段：初始季節(jié)因素調整

(12)

該移動平均能保留線性趨勢，消除12階不變季節(jié)性，并減少不規(guī)則成分方差。

(13)

從原序列中剔除趨勢循環(huán)分量后即得到季節(jié)-隨機成分。

(14)

式中：

(15)

即對每個月的觀測值分別進行3×3的季節(jié)移動平均，將初步估計的季節(jié)成分剔除其2×12項簡單移動平均，以消除季節(jié)分量中的殘余趨勢。

(4)季節(jié)調整結果的初始估計

(16)

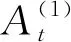
第二階段：精確季節(jié)因素調整

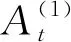
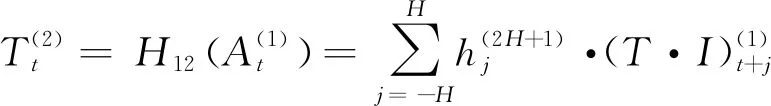
(17)

式中：H為Henderson加權移動平均項數，隨機分量I越大,需要的項數越多；h為Henderson加權移動平均系數。

(18)

(19)

式中：

(20)

(4)季節(jié)調整結果的二次估計

(21)

第三階段：估計最終的趨勢循環(huán)分量和隨機分量

(22)

(23)

最終得到季節(jié)分解乘法模型的各分量序列

(24)

按照式(24)方法提取出月度客運量序列中的趨勢循環(huán)分量、季節(jié)分量和隨機分量，見圖4～圖6。

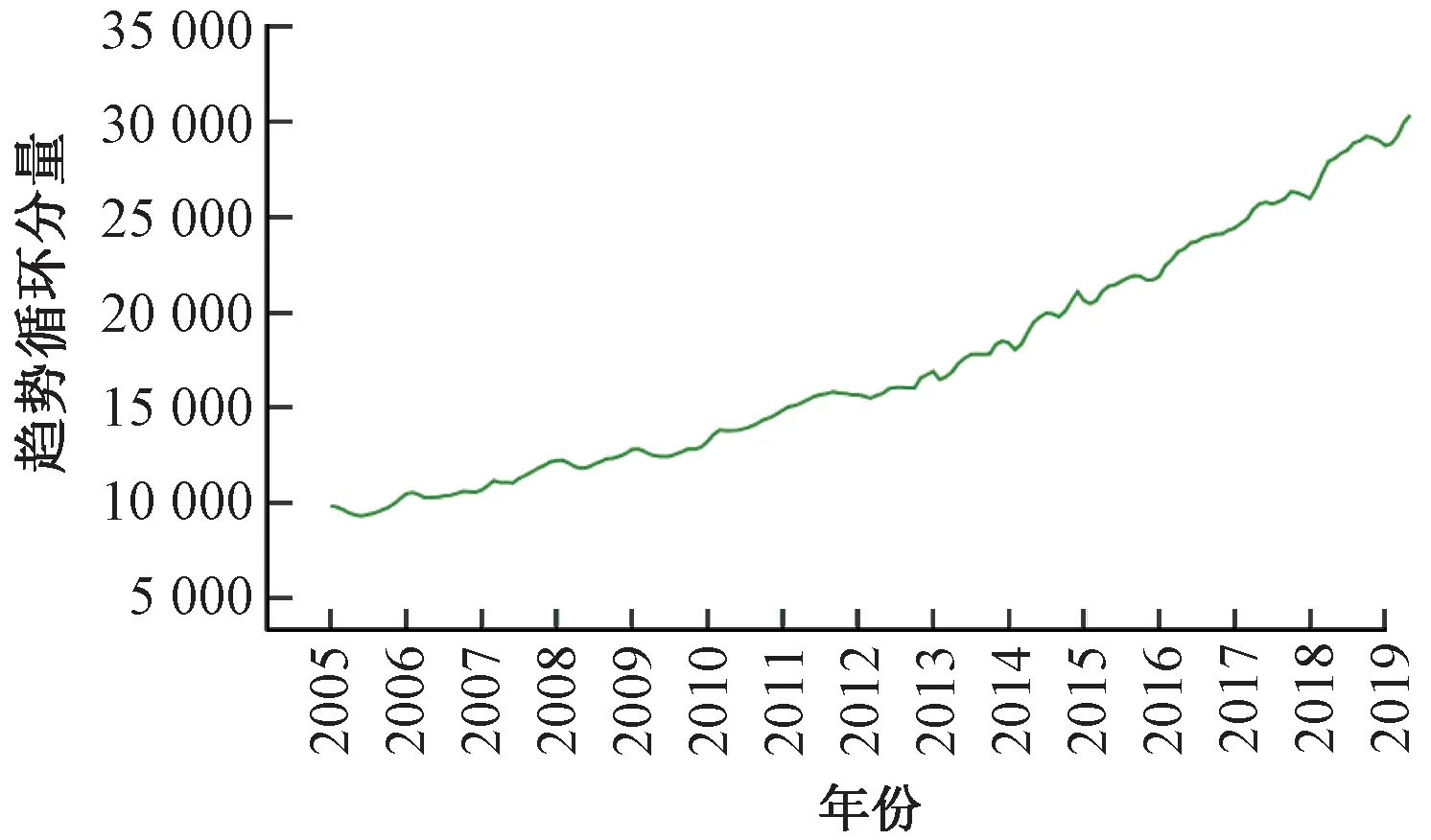
圖4 鐵路月度客運量趨勢循環(huán)分量Tt

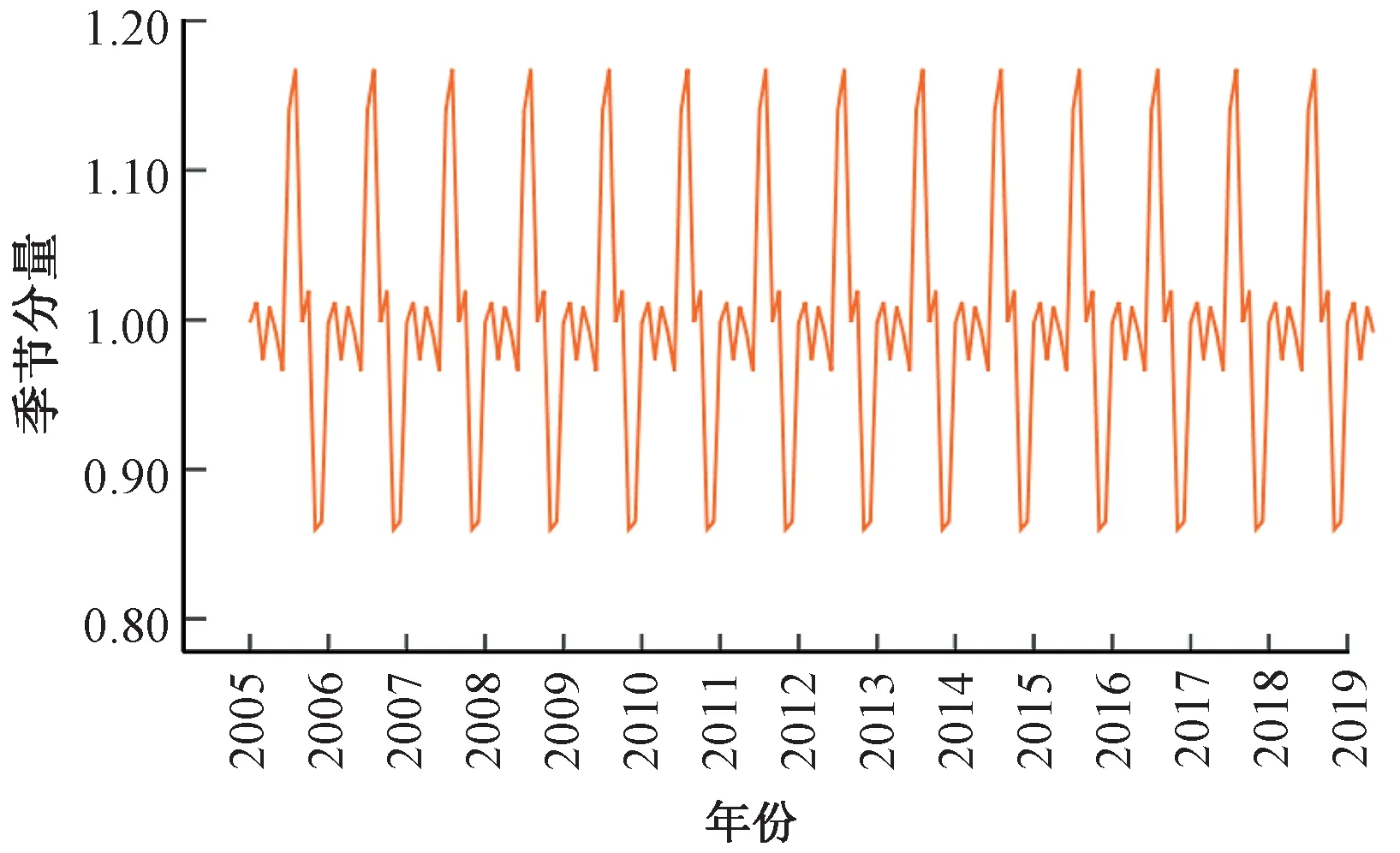
圖5 鐵路月度客運量的季節(jié)分量St

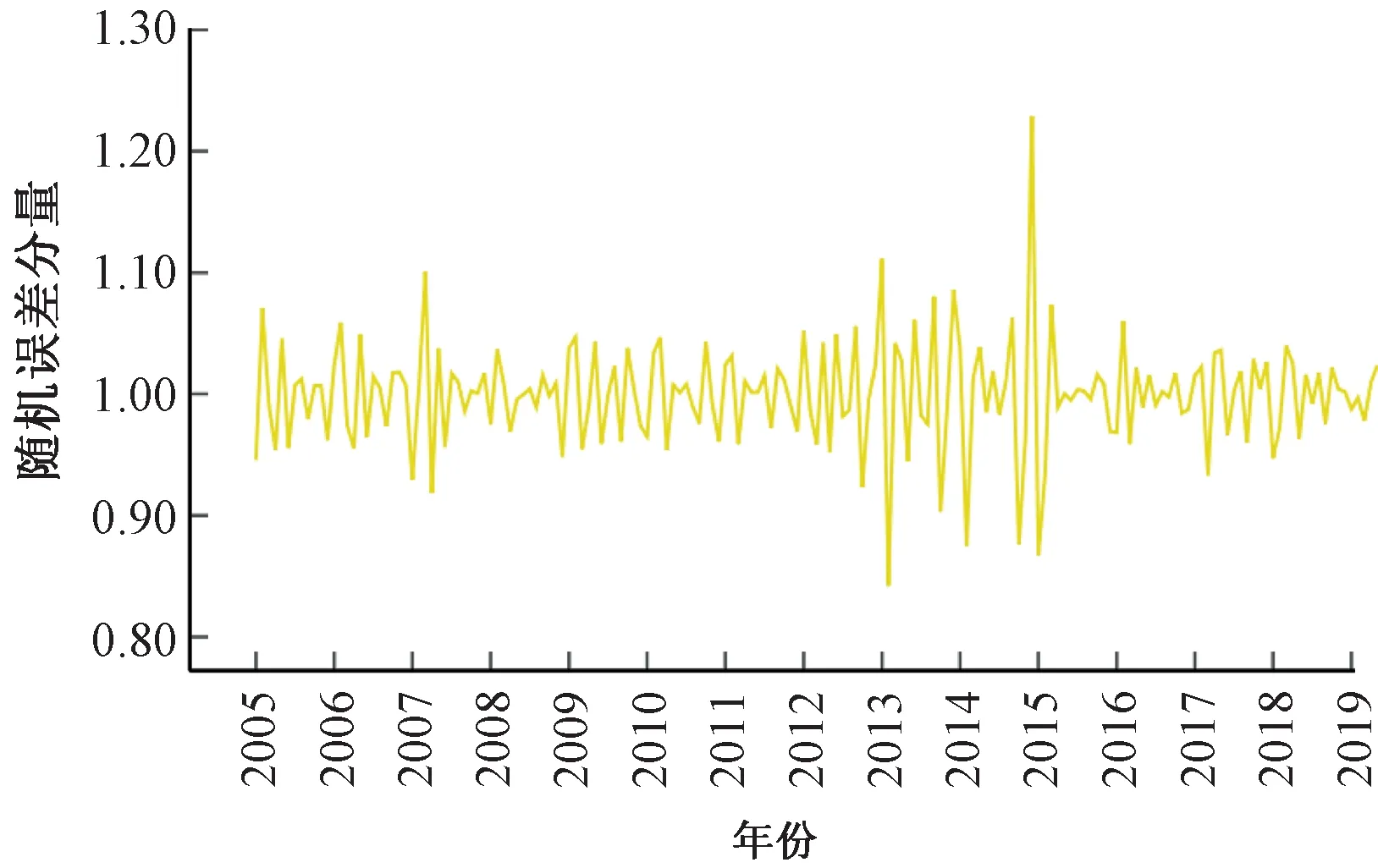
圖6 鐵路月度客運量的隨機分量It

從月度客運量序列的成分分解時序圖可見，客運量各分量隨時間的變化特性差異較大，呈現明顯的趨勢性、季節(jié)周期性以及隨機性特征。所以，鐵路月度客運量時間序列適宜采用乘法季節(jié)模型進行預測。

3 月度客運量的SARIMA-GARCH預測模型構建

經上述量化檢驗和分析可知，對數序列LY經一階差分后平穩(wěn)。因此，可以對LY序列進行建模。

3.1 SARIMA(p,d,q)(P,D,Q)s基礎模型構建

(1)確定周期s和差分次數d、D

本文以月度數據為研究樣本，即周期s取12。同時，從LY的相關圖7也可以看出，其自相關系數呈線性緩慢衰減，在滯后期為12的整倍數時點上出現自相關系數絕對值較大的峰值；這在ΔLY序列的相關圖8中體現尤其明顯，12的整倍數時點出現峰值，且呈振蕩式衰減變化。

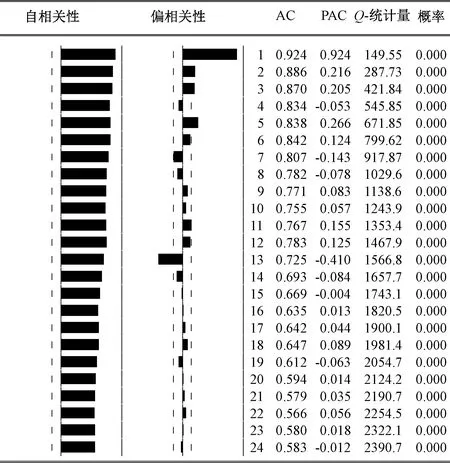
圖7 對數序列LY的自相關、偏相關圖

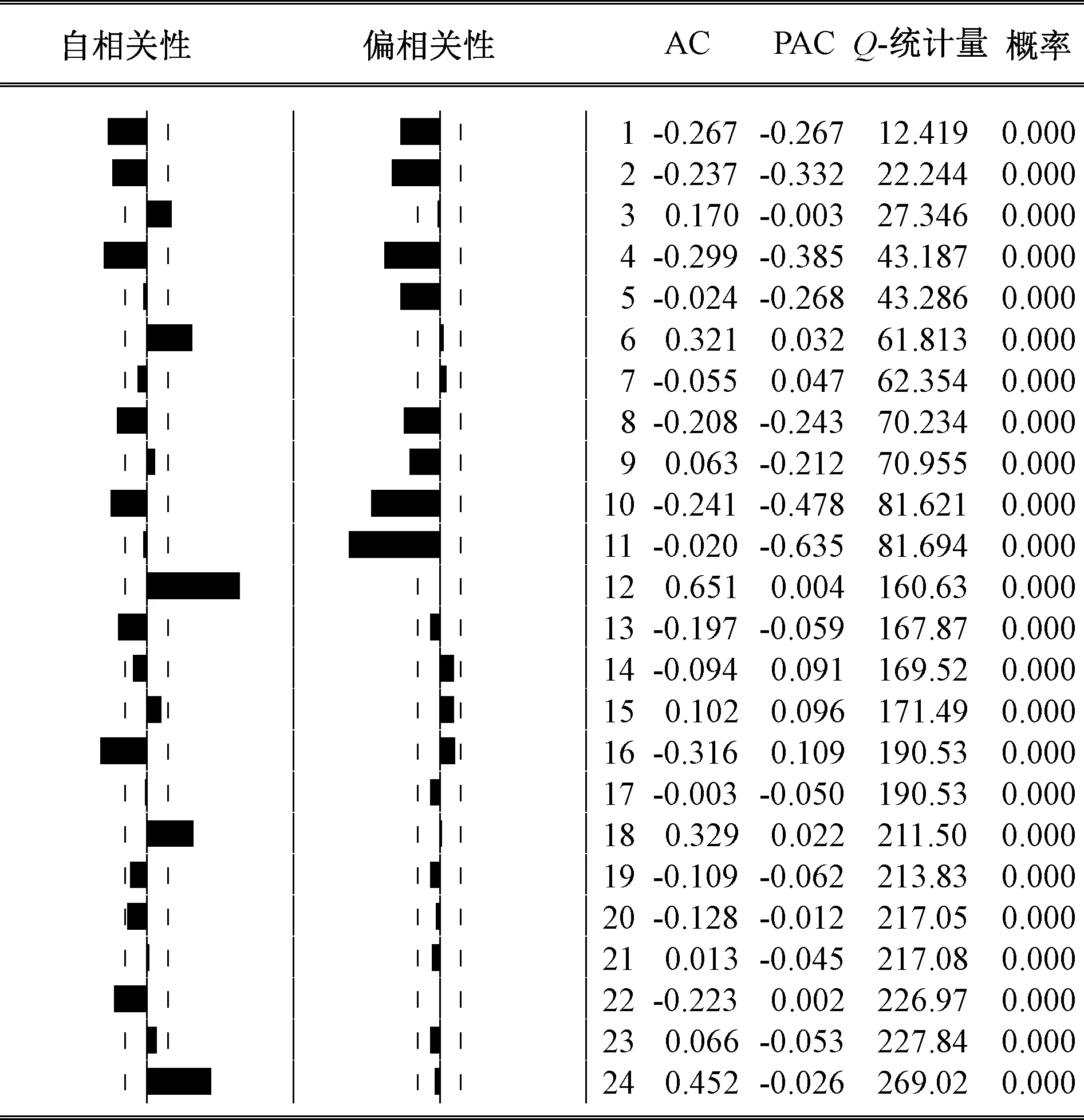
圖8 一階差分序列ΔLY的自相關、偏相關圖

這足以證明序列存在顯著的以12為周期的季節(jié)波動，這與實際情況一致。因此，需對其進行季節(jié)性差分(或12階差分)。對數序列LY的一階差分ΔLY平穩(wěn)，即非季節(jié)差分次數d取1。對ΔLY進行一次季節(jié)性差分后得到ΔΔ12LY序列，其時序圖見圖9、相關圖見圖10。

由圖9可知ΔΔ12LY序列圍繞0軸上下小幅波動，呈現良好的平穩(wěn)性。同時，圖10也顯示在滯后期12的整倍數時點處的相關系數在2倍標準差范圍內，說明其季節(jié)性成分已被充分提取。綜上，季節(jié)性差分次數D取1可滿足平穩(wěn)性要求。

(2)模型階數判別

觀察圖10，結合表2的模型階數判別方法，可以看到自相關和偏相關圖都呈欠阻尼狀態(tài)震蕩衰減，非季節(jié)自相關系數呈1階或2階截尾，即非季節(jié)項AR的階數p可取1或2。同時，由于平穩(wěn)序列ΔΔ12LY中大部分季節(jié)性波動已被消除，其周期12整倍數時點的季節(jié)自相關系數在2倍的標準差范圍緩慢衰減，自相關性明顯減弱，說明針對該序列建立滯后1階和12階上的SARIMA 模型是合適的，即模型的非季節(jié)項MA的階數q取1，季節(jié)項SMA的階數Q也取1。季節(jié)項SAR的階數P可取0(按拖尾衰減處理)或1(按1階截尾處理)。據此，可初步確定符合要求的四個SARIMA(p,d,q)(P,D,Q)12模型：(1,1,1)(0,1,1)12、(1,1,1)(1,1,1)12、(2,1,1)(0,1,1)12和(2,1,1)(1,1,1)12。

圖9 ΔΔ12LY的時序圖

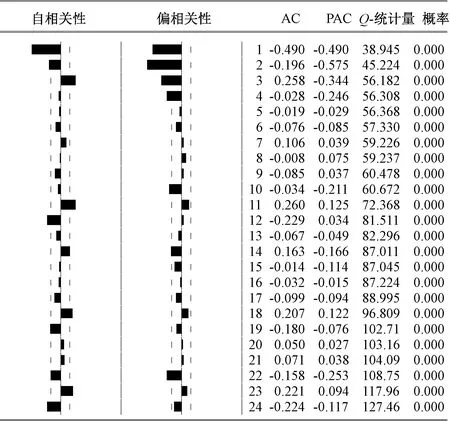
圖10 ΔΔ12LY的自相關、偏相關圖

(3)SARIMA模型擬合優(yōu)度檢驗及篩選

對上述4個備選季節(jié)模型進行擬合優(yōu)度檢驗，見表3。

表2 模型階數判別表

表3 模型擬合優(yōu)度檢驗結果

表3中的調整后可決系數R2表示模型的整體擬合優(yōu)度，取值范圍[0,1]，該值越大表示模型擬合效果越好。赤池信息量準則AIC、施瓦茨信息量準則SC取值越小表明模型擬合精度越高。DW值表示模型殘差的不相關程度，范圍在0～4之間，該值越接近2表明自相關程度越低，建模效果越好。通過表3的檢驗結果對比，SARIMA(2,1,1)(1,1,1)12模型的可決系數R2最大，AIC和SC值最小，DW統(tǒng)計值最接近2，多項指標均顯示其檢驗結果為最優(yōu)，因此，最終選定SARIMA(2,1,1)(1,1,1)12模型對樣本序列建立基礎模型。

(4)SARIMA模型參數估計

取2005年1月—2018年12月期間的數據作為訓練樣本運用OLS方法估計出SARIMA(2,1,1)(1,1,1)12模型方程為

(1+0.420 2L+0.408 6L2)(1-0.323 3L12)ΔΔ12LYt=(1-0.661 0L)(1-0.797 6L12)vt

(25)

t統(tǒng)計量：(-4.821 3)(-4.498 6) (2.287 7) (-7.957 2) (-6.367 0)

R2為0.675 7，標準差(Standard Error,SE)為0.054 4，殘差平方和(Residual Sum of Squares,RSS)為0.441 7，AIC值為-2.893 1，SC值為-2.775 3

可見，該方程各參數統(tǒng)計量均較顯著，初步擬合效果較好。

3.2 SARIMA-GARCH融合模型構建

(1)SARIMA模型殘差的ARCH效應檢驗

在進一步構建GARCH(1,1)模型前，需對基礎模型SARIMA(2,1,1)(1,1,1)12殘差進行ARCH檢驗。首先，觀察SARIMA(2,1,1)(1,1,1)12模型殘差時序圖11，發(fā)現殘差波動存在“集聚”現象：波動在一些時段內較小，在一些時段內又變得很大。據此初步判斷殘差序列存在ARCH效應。

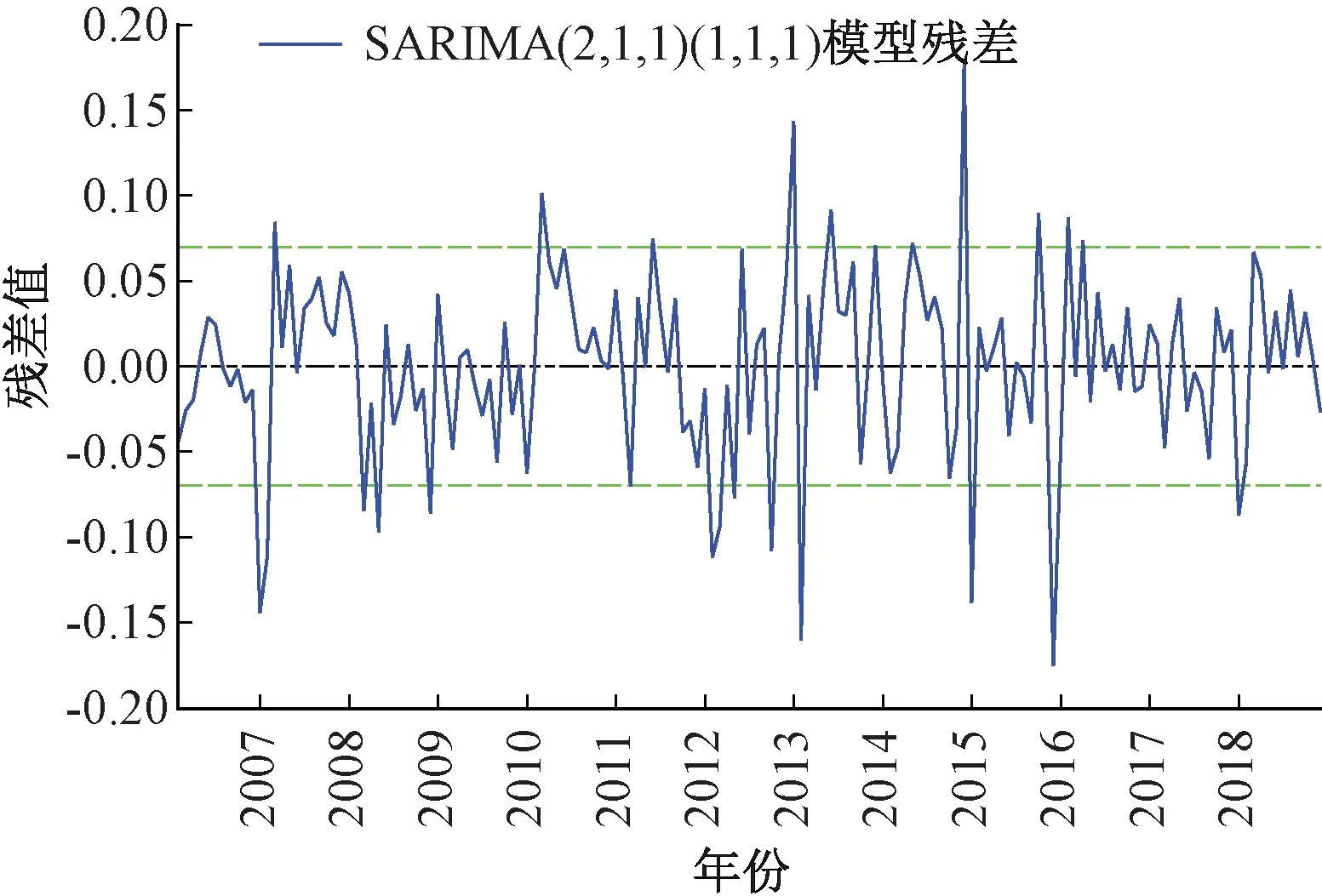
圖11 SARIMA(2,1,1)(1,1,1)12模型殘差時序圖

為進一步證實模型殘差序列具有ARCH效應，本文采用White檢驗法對其進行ARCH效應量化檢驗。檢驗結果見表4。

表4 SARIMA(2,1,1)(1,1,1)12模型殘差ARCH檢驗結果

從表4中可見，F統(tǒng)計量、LM統(tǒng)計量均顯著，其接受殘差序列是同方差的原假設的相伴概率P值都為0，即拒絕原假設，殘差序列存在顯著的異方差。

(2)構建SARIMA-GARCH融合模型

在SARIMA(2,1,1)(1,1,1)12的基礎上考慮ARCH效應后重新對序列進行極大似然估計，可得SARIMA(2,1,1)(1,1,1)12-GARCH(1,1)融合模型為

均值方程：(1+0.399 1L+0.407 3L2)(1-0.248 0L12)ΔΔ12LYt=(1-0.652 5L)(1-0.898 6L12)vt

(26)

t統(tǒng)計量： (-4.584 0) (-4.368 3) (3.443 2) (-8.487 1) (-44.309 3)

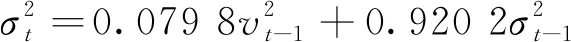
(27)

t統(tǒng)計量： (2.068 4) (23.840 2)

R2為0.902 3，SE為0.033 0，RSS為0.381 9，AIC值為-3.994 8，SC值為-3.879 3

與式(25)的SARIMA模型相比，考慮了條件異方差所建立的SARIMA-GARCH融合模型擬合優(yōu)度R2有了較大改善，參數統(tǒng)計量更為顯著，標準差、殘差平方和以及AIC、SC值也顯著縮小。均值方程各參數估計值有小幅修正，方差方程ARCH項、GARCH項系數均統(tǒng)計顯著。ARCH、GARCH項系數都為正，滿足了參數約束，系數之和近似為1，表現出良好的收斂性。這充分說明SARIMA-GARCH融合模型能更好地擬合鐵路月度客運量數據。

3.3 模型穩(wěn)定性檢驗

得到SARIMA-GARCH模型后，為避免擬合過程中還有重要信息丟失，需進一步檢驗模型的穩(wěn)定性，即對殘差的異方差效應和自相關性進行檢驗分析，若模型不穩(wěn)定則解釋力有限。

(1)模型殘差的ARCH-LM檢驗

采用ARCH-LM方法檢驗方程殘差的條件異方差，結果見表5。

表5 SARIMA-GARCH模型殘差ARCH檢驗結果

檢驗得到F統(tǒng)計量、LM統(tǒng)計量均不顯著，相伴概率P值均為0.55，即接受同方差的原假設，說明引入GARCH模型后消除了原殘差序列的異方差效應。

(2)模型殘差的平方相關圖檢驗

通過殘差平方相關圖和Q-統(tǒng)計量對模型殘差進行檢驗，見圖12。

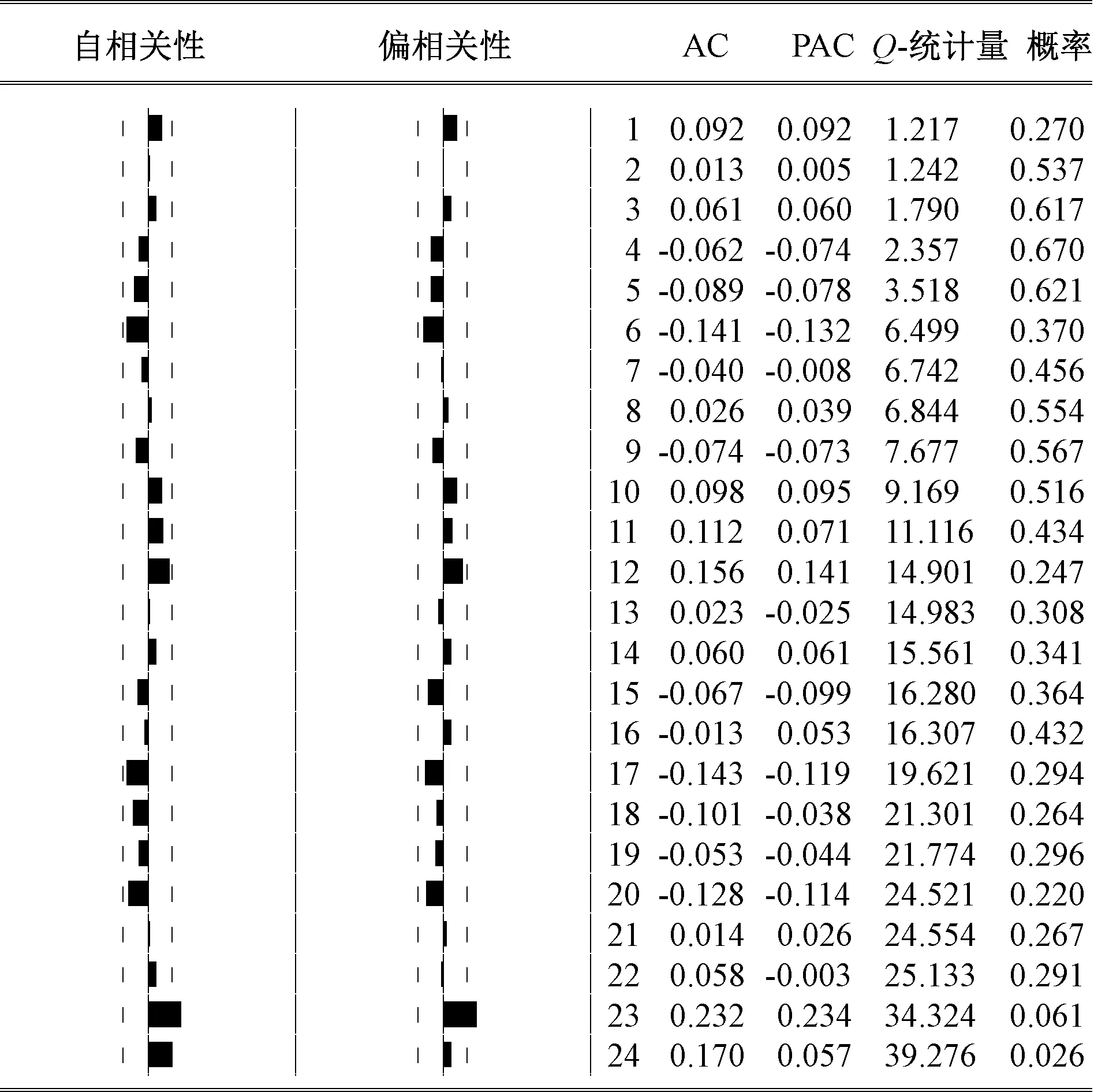
圖12 SARIMA-GARCH模型殘差平方相關圖

由圖12可知，模型殘差的ACF和PACF值均顯著地落在2倍的標準差范圍內，自相關和偏自相關系數近似為0，殘差序列為同方差的原假設的相伴概率值均大于10%，可以認定殘差序列為白噪聲，即模型已將原時間序列的信息基本提取完畢。

綜上，所建SARIMA-GARCH穩(wěn)定性良好，對建模數據的解釋力較強。

4 模型預測精度驗證對比及性能評價

為驗證所建模型的有效性，將SARIMA-GARCH模型與常規(guī)SARIMA、ARIMA和NAR動態(tài)神經網絡等時序模型的短期預測值進行精度對比，并對該模型的中長期預測效果進行分析。

4.1 模型短期預測精度對比

以2019年1—5月份的客運量數據作為測試樣本，將SARIMA(2,1,1)(1,1,1)12-GARCH(1,1)模型與SARIMA(2,1,1)(1,1,1)12、ARIMA(2,1,1)和NAR動態(tài)神經網絡模型的短期預測值進行精度對比見表6。

對比表6中4種模型的短期測算結果，可以看到所構建的SARIMA-GARCH融合模型與SARIMA基礎模型的穩(wěn)定性更好，平均絕對百分誤差均小于5%，而ARIMA模型和NAR動態(tài)神經網絡模型的穩(wěn)定性要差些，平均絕對百分誤差也大于5%。這表明，前兩類模型在對具有季節(jié)性變化的時間序列建模時更具優(yōu)勢，其建模效果較好。同時，由于SARIMA-GARCH融合模型考慮了時間序列中存在的異方差效應，提高了對波動性的刻畫精度，使得預測值與實際值接近程度更高、偏差更小，短期預測精度比單純的SARIMA模型更好。因此，所建模型的數據擬合能力較強，短期測算精度較高。

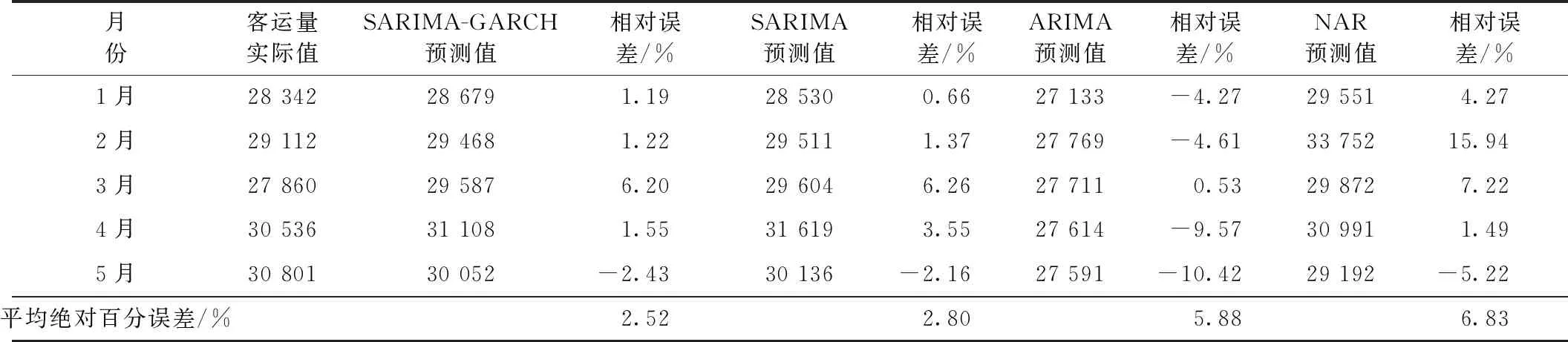
表6 2019年1—5月鐵路月度客運量預測誤差比較

4.2 模型中長期預測性能評價

本文選取平均相對誤差δMPE、Theil不等系數U、偏差比σBP、方差比σVP和協(xié)方差比σCP等多個評價指標對模型中長期預測性能進行驗證評價。

(1)平均相對誤差δMPE

(28)

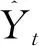
(2)Theil不等系數U

(29)

(3)偏差比σBP

(30)

(4)方差比σVP

(31)

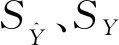
(5)協(xié)方差比σCP

(32)

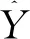
以2005年1月為基期，利用所建SARIMA-GARCH模型對鐵路月度客運量進行中長期測算，測算值與相應月份客運量實際值的對比效果見圖13。

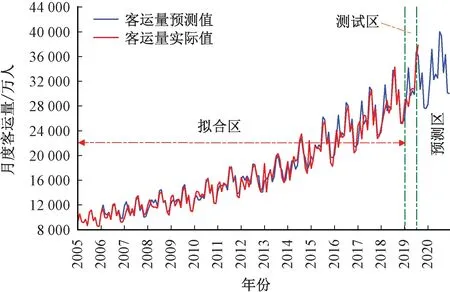
圖13 SARIMA-GARCH模型中長期預測值與實際值對比圖

從圖13可見，建模期內(2019年虛線軸左側區(qū)域)模型的中長期預測值與真實值的擬合程度也比較好。各項預測性能指標：平均相對誤差MPE為5.69%，高于短期測試區(qū)(2019年1月至2019年5月條形區(qū)域)的相對誤差MPE值2.52%；Theil不等系數U為0.043 7，它是不受量綱影響的相對指標，度量的是相對均方誤差；偏倚比σBP為0.114 2，它表示的是系統(tǒng)誤差，度量了預測值與實際值序列均值的偏離程度；方差比σVP為0.008 2，該值較小近乎為0，度量了預測值方差與實際值方差的偏離程度；協(xié)方差比σCP為0.877 6，略低于0.9，它衡量了剩余的非系統(tǒng)預測誤差及模型的預測穩(wěn)定性。若預測效果良好，則偏倚比σBP和方差比σVP都會比較小，而協(xié)方差比σCP會比較大，且三者之和為1。

比較而言，SARIMA-GARCH模型的中長期預測精度較短期預測有所降低，表明該模型更適合作短期預測。

5 結論

本文通過季節(jié)分解法量化分解出鐵路月度客運量時間序列中的趨勢循環(huán)分量、季節(jié)分量和不規(guī)則波動分量。然后，對時間序列平穩(wěn)化、單整性處理后引入SARIMA模型對其季節(jié)性、趨勢性進行基礎建模。為進一步提高對波動性的刻畫精度，消除異方差性，對基礎模型殘差構建了GARCH模型，得到SARIMA-GARCH融合模型。最后，為驗證該模型的穩(wěn)定性和實用性，將其與常規(guī)的SARIMA、ARIMA和NAR動態(tài)神經網絡模型短期預測值進行精度對比分析，同時對其中長期預測效果作了測試分析。研究結果表明：

(1)鐵路月度客運量具有顯著的趨勢性、季節(jié)性和波動性特征。鐵路客運組織部門需在總體滿足旅客出行需求逐漸增長的前提下，靈活地根據各月份客運量的季節(jié)性波動合理制定列車開行計劃和車底運用方案。

(2)鐵路月度客運量時間序列是非平穩(wěn)、非線性及存在異方差效應的。在對其進行建模預測時，為確保預測精度，不能忽視其單整性和異方差性的影響。

(3)綜合考慮了月度客運量序列的趨勢性、季節(jié)性和波動性的SARIMA-GARCH模型能很好地擬合數據，短期預測性能良好。

基于SARIMA-GARCH的月度客運量預測模型豐富了鐵路運輸組織的優(yōu)化理論體系，可為鐵路客運組織部門制定設備運用方案或日常運營計劃提供科學的決策參考。