考慮多交路多編組的城市軌道線路列車交路計劃優化

李正洋，趙 軍，彭其淵

(1. 西南交通大學 交通運輸與物流學院，四川 成都 611756；2. 西南交通大學 綜合交通運輸智能化國家地方聯合工程實驗室，四川 成都 611756)

城市軌道交通線路的列車交路計劃主要規定了該線路在給定時段所運營的列車交路條數、各交路的折返站、列車編組及相應的開行頻率等重要技術參數，是城市軌道交通線路行車組織的基礎性計劃。在設計一條新建線路或調整一條運營線路的行車組織計劃時，首要工作是確定該線路在給定時段的列車交路計劃，以為后續全日行車計劃編制、列車運行圖編制及運力資源配置等提供依據。科學合理地編制列車交路計劃，對于提高城市軌道交通線路的行車組織效率、降低企業運營成本、增加乘客出行滿意度具有重要作用。

目前，采用單一全程大交路，并根據最大區間斷面客流量確定列車編組與開行頻率仍是現場常用的城市軌道交通線路列車交路計劃編制方法。在此方法下，線路上各區間輸送能力相同。但該方法未考慮到客流需求的空間分布不均衡性，可能導致線路上部分區間輸送能力浪費，部分區間輸送能力緊張。針對此問題，一種常用的解決辦法是采用多交路多編組的列車交路模式，即線路上運營多條列車交路，不同交路還可采用不同的列車編組。工程實踐經驗表明，該模式可使城市軌道交通線路上的不同區間配備不同的輸送能力，使得線路的輸送能力在空間上更加匹配客流需求，從而有效降低運營企業成本和乘客出行時間成本。

國內外對具有多交路或多編組的公共交通線路的交路設計問題開展了一定研究工作。國外針對公交線路的相關研究主要聚焦于大小交路模式下公交時刻表優化[1-2]及小交路折返點與發車頻率優化[3-5]。針對城市軌道交通線路，Sun等[6]取消全程大交路存在的假設，提出了具有多交路單編組列車交路設計問題的非線性規劃模型；Ding等[7]考慮高峰小時線路負荷，提出了大小交路單編組問題的非線性規劃模型。國內研究主要集中于城市軌道交通線路的大小列車交路設計問題。王媛媛等[8]以乘客出行時間成本與企業經營成本最小為目標，建立了大小交路單編組問題的非線性規劃模型；許得杰等[9]以乘客等待時間與企業運營成本最小為目標，建立了大小交路多編組問題的優化模型；史芮嘉等[10]考慮線路的輸送能力利用均衡性，以輸送能力利用率最大、上線車組數和乘客出行費用最小為目標，建立了大小交路多編組問題的非線性規劃模型。此外，程婕等[11]研究了多交路單編組問題，以快速車底周轉和換乘客流最少為目標，提出了混合整數規劃模型；李得偉等[12]研究了Y型線路的多交路單編組列車交路問題，以企業成本和乘客成本最小為目標，提出了考慮乘客出行行為的整數規劃模型。

可見，具有多交路多編組的城市軌道交通線路列車交路設計問題尚未被完整探討過，既有研究還存在以下問題。首先，既有文獻大多是研究大小交路模式下的列車交路設計問題，即在全程大交路存在的假設下，優化小交路的相關參數。當考慮多交路運營時，許多現有模型不再適用。目前一些城市軌道交通線路上的運營交路數量已超過2條，如上海地鐵2號線(3交路)、重慶軌道交通3號線(3交路)，有必要對多列車交路設計問題進行研究。其次，在全程大交路存在的假設下，大部分既有文獻假設乘客可乘坐直達列車前往其目的地，很少有文獻分析乘客在1條線路上出行時，對不同交路列車的選擇行為，尤其是在多交路條件下的乘客始發與換乘過程中的列車選擇行為。此外，列車編組也是交路計劃中的一項重要參數，其與列車開行頻率共同決定了城市軌道交通線路的輸送能力，若允許不同的交路配置不同的列車編組，并將列車交路與列車編組進行綜合設計，可能獲得與客流需求匹配更好的列車交路計劃。

本文研究多交路多編組運營模式下城市軌道交通線路列車交路設計的優化方法。首先，根據線路的折返站布置生成所有備選交路，進而構建1個服務網絡。基于此，采用Spiess等[13]的最優策略在服務網絡上進行客流分配，描述乘客對不同交路列車的選擇行為。然后，以運營企業成本和乘客等待時間成本最小為目標，提出多交路多編組列車交路設計問題的優化模型與求解方法。最后，采用實際案例驗證了所提出方法的可行性和有效性。

1 問題描述與假設

1.1 問題描述

本文考慮具有多交路和多編組的直線型城市軌道交通線路的列車交路設計問題。該線路有2條正線，一條正線只供一個方向的列車運行。線路上有多個車站，根據配線設置分為可供列車轉向的折返站和不可供列車轉向的普通站。車站將線路拆分為若干區間，各區間的端點可為折返站或普通站。列車在線路上周轉運行，在每次周轉過程中，列車從始發站出發，沿著一條正線運行至終到站，在終到站折返后，沿著另一條反向正線回到始發站，在始發站折返后，進入下一次周轉過程。現場將線路上列車固定周轉運行的區段稱為列車交路，各交路的端點只能是折返站，且各交路上的列車成對運行。

以圖1所示線路為例，該線路含7個車站和6個區間，車站沿上行方向依次編號為v1～v7，區間沿上行方向依次編號為e1～e6。車站v1、v4、v7為折返站，其中，車站v1、v7為單向折返站，車站v1只能將列車從下行折返為上行，車站v7只能將列車從上行折返為下行，車站v4為雙向折返站，在上下行方向上均能折返列車。根據折返站布置，該線路最多可設置3條列車交路，包括在車站v1、v7間設置交路1，在車站v1、v4間設置交路2，在車站v4、v7間設置交路3。其次，各交路可采取不同的列車編組，例如交路1使用8編組列車，交路2使用6編組列車，交路3使用6編組列車。最后，各交路可開行不同對數的列車，例如交路1、2和3分別開行12對、6對和6對列車。

圖1 線路示意圖

列車交路計劃同時影響運營企業與乘客的利益。一方面，列車交路計劃決定了城市軌道交通線路運營所需的車底數量與工作人員數量；另一方面，列車交路計劃對乘客的出行時間也有顯著影響。因此，制定列車交路計劃時，要盡量降低運營企業的成本并節省乘客的出行時間成本。同時，可行的列車交路計劃還需滿足車站和區間的覆蓋要求、區間的客流需求、折返站能力和線路通過能力以及特殊的運營組織規則等條件的限制。如何根據研究線路的車站布局、可行的列車編組形式、給定時段的客流需求、區間通過能力、車站折返能力及其他運營組織規則等信息，確定列車交路、列車編組和開行頻率的最優組合，使得運營企業成本與乘客出行時間成本最小，即為城市軌道交通線路列車交路設計優化問題。

1.2 問題假設

為便于模型建立，做出以下假設：

(1)乘客的乘車行為符合最優策略原則[13]，即在各車站，乘客在到達車站后，乘坐可前往其目的地方向的第一列經過該車站的列車。

(2)各車站乘客均勻到達，列車按時刻表均勻到達，無乘客滯留。

(3)各交路的車底獨立運用，一個交路只能采用一種編組的列車，但不同交路可采用不同編組的列車。

(4)不同交路不同編組的列車均站站停，且在同一區間具有相同的運行時間。

2 模型構建

2.1 網絡抽象

根據城市軌道交通線路的折返站布置，可生成其所有的備選列車交路，并基于此將其抽象為1個有向服務網絡，在該服務網絡上進行列車交路設計和客流分配。以圖1所示線路為例，該線路具有3條備選列車交路，其對應的有向服務網絡見圖2。

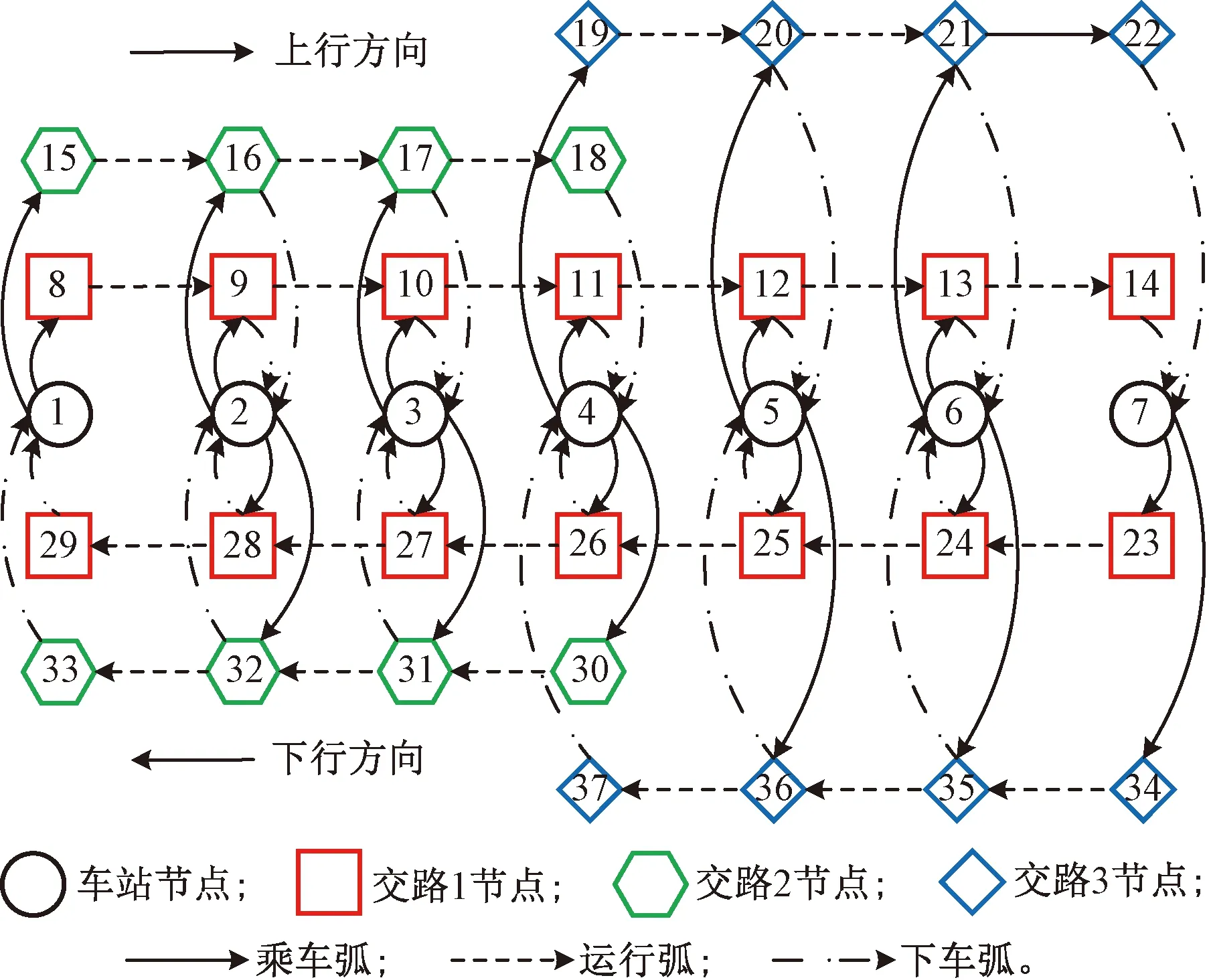
圖2 服務網絡示意圖

服務網絡中，節點集由兩部分構成，包括車站節點1～7與交路節點8～37。車站節點1～7表示線路上的車站v1～v7，交路節點表示各備選交路對線路上各車站的覆蓋。交路1覆蓋車站v1～v7，因此，交路1所對應的節點8～14、23～29平行覆蓋車站節點1～7。交路2覆蓋車站v1～v4，因此，交路2所對應的節點15～18、30～33平行覆蓋車站節點1～4。交路3覆蓋車站v4～v7，因此，交路3所對應的節點19～22、34～37平行覆蓋車站節點4～7。交路節點中，節點8～22為上行方向節點，節點23～37為下行方向節點。

弧集由3部分組成，分別為乘車弧、運行弧與下車弧。乘車弧連接車站節點與其對應的交路節點，表示乘客在對應車站乘坐對應交路上去往對應方向列車的乘車行為。在上下行方向上，運行弧依次連接同一交路的各交路節點，表示各交路上的列車在上下行方向的區間運行過程。下車弧連接交路節點與其對應的車站節點，表示對應交路去往對應方向的列車上的乘客在對應車站的下車行為。注意，在各運行方向上，乘車弧不連接車站節點與各交路在該運行方向上的最后一個交路節點，下車弧不連接各交路在該運行方向上的第一個交路節點與車站節點。以上行方向為例，節點4與節點18間沒有乘車弧，因為交路2的列車不能將車站v4的乘客運往上行方向。節點19與節點4間沒有下車弧，因為車站v4是交路3在上行方向的始發車站，當交路3上行方向的列車到達車站v4時，車上還沒有乘客，因此不會產生乘客下車行為。

將研究線路基于上述規則抽象為有向服務網絡后，各支客流的乘客在線路上的出行過程(始發、運行、換乘、終到)即可用服務網絡中該支客流對應的始發車站節點至終到車站節點的路徑來表示。例如，若乘客于車站v1乘坐交路2的列車到達車站v4，然后換乘交路3的列車終到車站v6，其出行過程可用網絡中的路徑1-15-16-17-18-4-19-20-21-6表示。

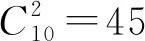
2.2 符號說明

集合：V、v分別為城市軌道交通線路的車站集合與索引，車站按上行方向編號，V={V1,V2}；V1為線路的折返站集合；V2為線路的普通站集合；E、e分別為城市軌道交通線路的區間集合與索引，區間按上行方向編號；L、l分別為線路的備選交路集合與索引；T、t分別為可行的列車編組集合與索引；D、d分別為列車運行方向集合與索引；F、f分別為可開行的列車集合與索引；N、n分別為服務網絡的節點集合與索引，N={N1,N2}；N1為服務網絡的車站節點集合；N2為服務網絡的交路節點集合；A、a分別為服務網絡的弧集合與索引，A={A1,A2}；A1為服務網絡的乘車弧集合，A1={A1 d|d∈D}，A1 d為服務網絡中運行方向d上的乘車弧集合；A2為服務網絡的運行弧與下車弧集合；An+為服務網絡中節點n處所有始發弧的集合；An-為服務網絡中節點n處所有終到弧的集合。

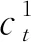
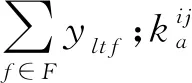
2.3 運營企業成本

城市軌道交通線路的運營企業成本主要包括固定成本與變動成本。固定成本指線路上所有投入使用的列車的總購置費用，注意，線路上的列車并非只在研究時段內運行，其使用年限一般為30年。為了便于與系統其他成本項具有可比性，將列車購置費用均攤至研究時段來作為固定成本。變動成本主要指線路上所有投入使用的列車在研究時段內的總運行費用，取決于研究時段內所有列車的總運行距離。運營企業固定成本Z1與變動成本Z2分別為

(1)

(2)

式(1)為研究時段內運營企業的固定成本，其中各交路所需的車底數量等于其全周轉時間乘以其開行頻率。式(2)為研究時段內運營企業的變動成本。

2.4 乘客等待時間成本

在1條城市軌道交通線路上，乘客出行時間主要由進站時間、始發或換乘等待時間、途中運行時間、出站時間4部分構成。線路的列車交路計劃幾乎不會對乘客的進、出站時間產生影響。同時，線路上不同交路的列車在同一區間的運行時間相同，乘客的途中運行時間也不會受到交路計劃影響。但是在不同的交路計劃下，線路上所采用的交路與各交路的開行頻率有所不同，會對始發或換乘乘客的候車時間產生影響，故考慮最小化乘客的等待時間成本。

理論上，1支客流在1個車站的乘客等待時間可取為該車站的乘客平均等待時間與該支客流在該車站的乘車人數的乘積。這里采用文獻[13]提出的最優策略在所構建服務網絡上進行客流分配，描述乘客在多交路上的出行過程以及對各交路列車的選擇行為，進而確定各車站乘客平均等待時間的期望值和各支客流在各車站不同交路列車上的乘客人數分布。最優策略[13]假設乘客均勻到達各車站，且乘坐前往其目的地方向的第一列經過該車站的列車，基于此，有兩點結論：

(1)各支客流(i,j)在服務網絡中各車站節點n、出行方向θij的乘客平均等待時間的期望值為該車站節點在θij方向上所有乘車弧所對應交路的列車開行間隔的一半，即

(2)各支客流(i,j)對從各車站節點n、出行方向θij發出的各乘車弧a的選擇概率為該乘車弧所對應交路的列車開行對數與從該車站節點在θij方向上發出的所有乘車弧對應交路的列車開行對數之和的比值，記客流(i,j)在從車站節點n發出的乘車弧a上的乘客人數為kij。

故乘客等待時間成本Z3為

(3)

2.5 基本模型

城市軌道交通線路列車交路設計最小化運營企業成本和乘客等待時間成本，即

(4)

目標函數式(4)中，第三部分(即乘客等待時間成本)為非線性表達式，會給模型求解帶來困難。根據最優策略，在服務網絡中，各支客流在各車站節點任意始發弧上的乘客人數等于該支客流在該車站節點的乘客總等待時間與該始發弧對應交路乘客平均等待時間的比值。利用這一關系，可通過引入約束確保客流分配符合最優策略，并獲得乘客等待時間成本的線性表達式。

由此，城市軌道交通線路列車交路設計問題的基本模型可構建為

(5)

(6)

(7)

(8)

(9)

(10)

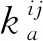
2.6 其他約束條件

基本模型式(5)～式(10)在最優策略下對服務網絡進行客流分配，其目的是獲得各支客流在服務網絡中的流量分布，并基于此計算乘客等待時間成本。還需引入車站和區間覆蓋要求、區間客流需求、特殊運營規則、車站和區間能力限制等約束條件，以此來設計可行的列車交路計劃，并計算運營企業的固定成本與變動成本。

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

yltf≥ylt,f+1?f∈[1,|F|-1],?l∈L,?t∈T

(20)

xlt=0或1 ?l∈L,?t∈T

(21)

yltf=0或1 ?l∈L,?t∈T,?f∈F

(22)

綜上，城市軌道交通線路列車交路設計問題可構建為以下混合整數非線性規劃模型TSD1為

目標函數 式(5)

s.t. 式(6)～式(22)

3 模型求解

3.1 模型線性化

?n∈N1,?i∈V,?j∈V

(23)

?n∈N1,?i∈V,?j∈V

(24)

?n∈N1,?i∈V,?j∈V

(25)

?n∈N1,?i∈V,?j∈V

(26)

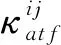
通過上述方法，模型TSD1可轉化為混合整數線性規劃模型TSD2，即

目標函數 式(5)

s.t. 式(6)、式(8)～式(26)

3.2 服務網絡簡化

初步計算分析表明，服務網絡規模對模型的規模與求解時間具有很大影響。鑒于列車交路只能設置于兩折返站之間，且在任意運行方向上位于兩相鄰折返車站節點tv1、tv2(tv2位于該運行方向上tv1的前方)中間的車站節點的乘客平均等待時間與tv1相同。基于此，提出簡化方法縮減服務網絡的規模，該方法不會影響模型求解結果的準確性。具體方法如下：

Step1在原服務網絡中，只保留折返站V1對應的車站節點與交路節點，并按前文類似規則生成弧。圖2中的服務網絡簡化后見圖3。

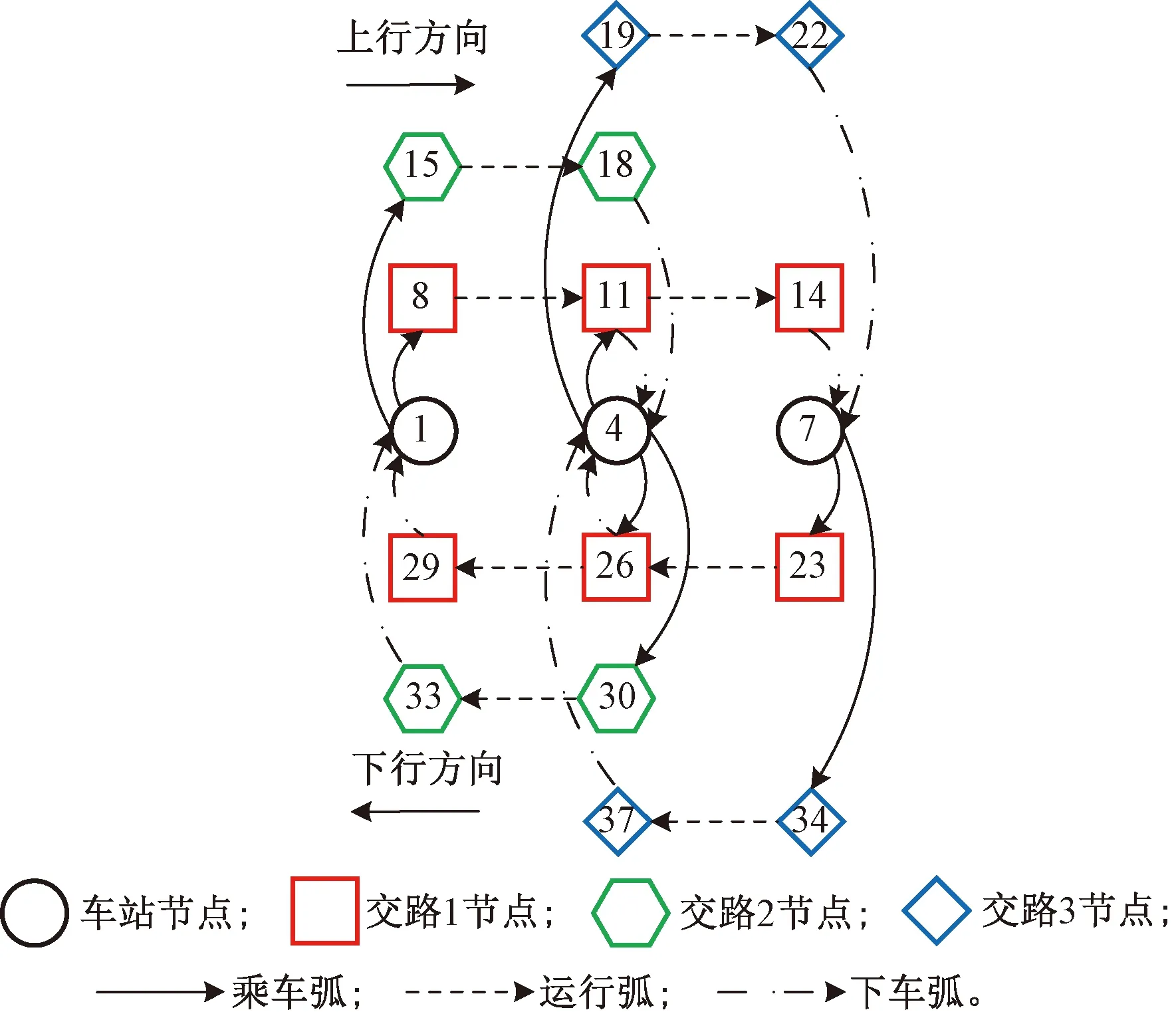
圖3 簡化服務網絡

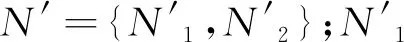
Step2對原服務網絡中各客流的始發節點、終到節點和客流量進行調整與集聚如下：

(1)若原服務網絡中某客流的始發節點和終點節點都是折返車站節點，則簡化網絡中該客流的始發節點和終到節點保持不變。

(2)若原服務網絡中某客流的始發節點不是折返車站節點，則在簡化網絡中將該客流的始發節點調整為其出行方向后方的最近折返車站節點。

(3)若原服務網絡中某客流的終到節點不是折返車站節點，則在簡化網絡中將該客流的終到節點調整為其出行方向前方的最近折返車站節點。

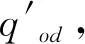
將服務網絡簡化后，模型TSD2可轉化為規模更小的混合整數線性規劃模型TSD3為

(27)

s.t. 式 (11)～式(22)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

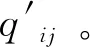
4 計算分析

以某規劃的城市軌道交通線路的實際數據構造算例，驗證所提出方法的有效性。采用MATLAB R2016a編程所提出方法，并調用CPLEX 12.8求解其中的優化模型。所有結果在CPU為Inter Core i7-7700 3.6 GHz，內存為16 GB的個人計算機上獲得。

4.1 案例描述

測試線路全長121.7 km，設車站20座，區間19個，按上行方向，車站依次標號為v1～v20，區間依次編號為e1～e19，見圖4。全線共設有4個折返站，分別為車站v1、v6、v17、v20。車站v1只能將列車從下行折返為上行，車站v20只能將列車從上行折返為下行，車站v6、v17在上下行方向上均能折返列車。折返站能力見表1。根據線路的折返站布置，共有備選列車交路6條，交路全周轉時間和距離見表2。線路上可運營4、6和8編組共3種類型的列車，列車編組參數見表3。選取規劃遠期一日早高峰時段08:00—09:00的客流數據進行列車交路設計，區間斷面客流見表4，限于篇幅，省略客流OD數據。其他輸入參數取值見表5。

圖4 測試線路(單位：m)

表1 折返站能力

表2 交路全周轉時間和距離 min/km

表3 列車編組參數

表4 區間斷面客流 人次

表5 其他參數

4.2 計算結果4.2.1 模型性能

將模型TSD2和TSD3進行對比，以評估所提出服務網絡簡化方法的正確性和有效性。為此，將最大允許交路數量Ω的取值從1遞增到6，共構造6個算例。將模型求解時間限制為4 h，模型對比結果見表6，其中，第2到第4列為模型TSD2獲得解的目標值、最優誤差和計算時間，最后3列為模型TSD3的相應結果。由表6可得，在限制時間內，模型TSD2只能將Ω=1的算例求得最優解，對其他算例只能找到質量差的可行解，誤差范圍為39%～94%。與模型TSD2不同，模型TSD3可極快獲得所有算例的最優解，最長計算時間不超過20 s。可以看出，所提出的簡化方法可保證計算結果的正確性，有效縮減服務網絡和模型的規模，提高求解速度，適用于求解實際規模的城市軌道交通線路列車交路設計問題。

表6 模型對比結果

4.2.2 列車交路計劃質量

現對比分析所提出優化方法獲得的多交路計劃(MTSS)與研究線路可研報告中由經驗方法設計的大小交路計劃(PTSS)的質量。為獲得MTSS，設置Ω為6，并求解模型TSD3到最優，最優解共設置4條交路。兩種方法下的列車交路計劃見圖5。

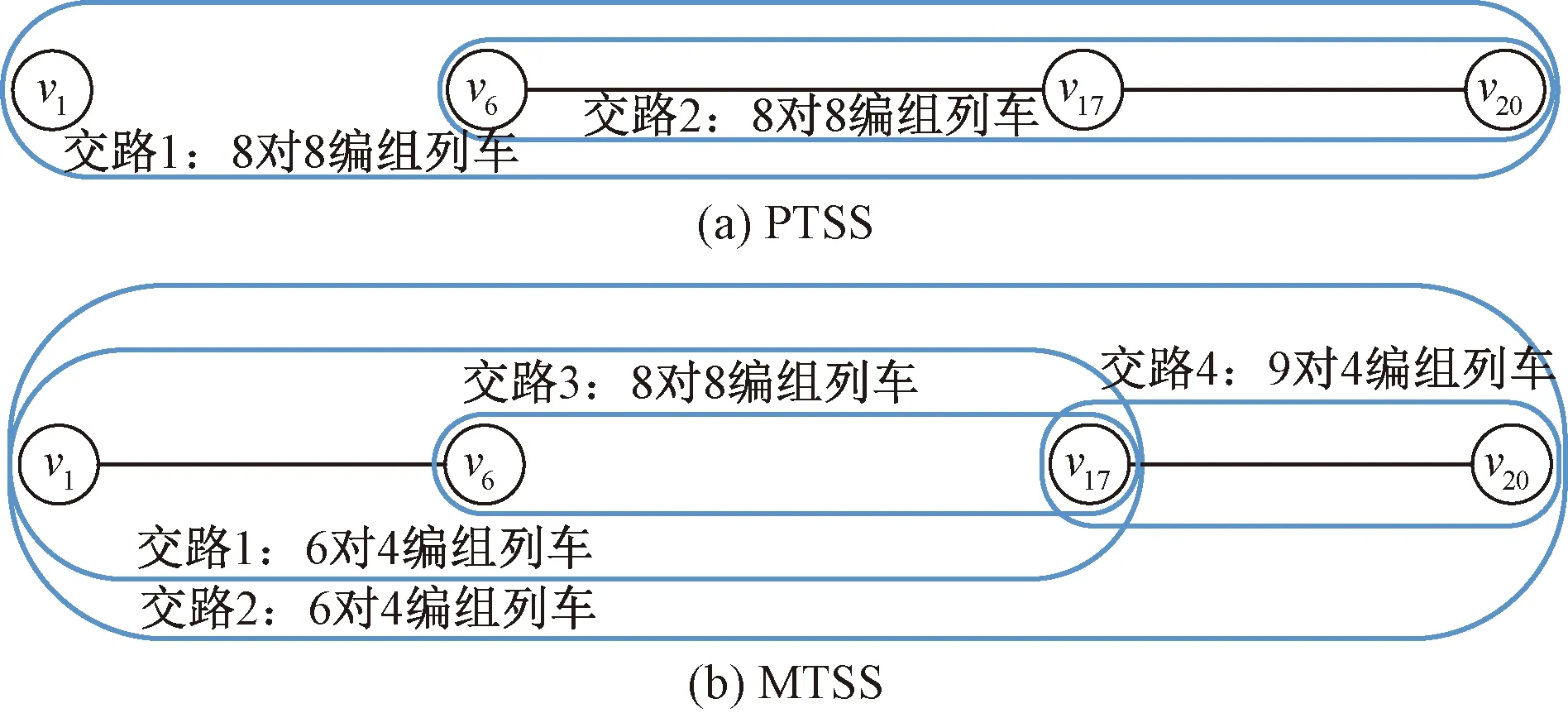
圖5 列車交路計劃

兩種交路計劃下的乘客換乘過程分析如下。在PTSS下，線路上運營一個全程大交路與一個小交路，部分乘客出行時需換乘一次。在MTSS下，線路上部分乘客出行時需換乘2次。例如，從車站v20始發前往車站v1的部分乘客的出行過程可為v20-交路4-v17-交路3-v6-交路1或交路2-v1，全程換乘2次。需要說明的是，線路上只有從車站v18～v20始發前往車站v1～v5的乘客才可能進行兩次換乘，此部分乘客僅457人，占全線總客流的0.41%。

兩種交路計劃下區間的輸送能力、客流需求和滿載率見圖6。不難看出，PTSS對區間客流量的不均衡性已有所考慮，但其在區間e17～e19仍有明顯的輸送能力浪費。相較之下，MTSS對各區間輸送能力的配置更為靈活，其不僅在區間e17～e19的輸送能力更低，滿載率更高，且在區間e1～e16的輸送能力也更貼近客流需求，有助于降低運營企業成本。

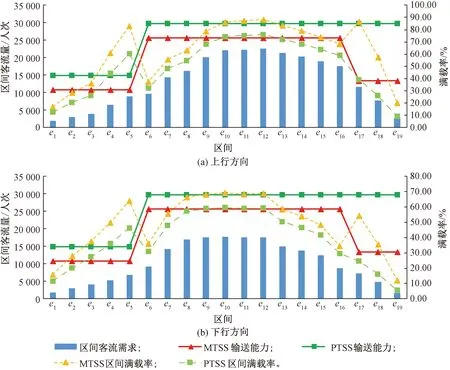
圖6 區間輸送能力配置

兩種交路計劃的目標值統計見表7，其中第4列為MTSS相對于PTSS的變化量。根據表7，與PTSS相比，MTSS將總成本降低22.14%，其中，MTSS下的企業固定成本、企業變動成本與乘客等待時間成本均有所降低。另外，在MTSS的總成本中，企業變動成本占81.06%，而企業固定成本僅占2.37%。因此，在設計城市軌道交通線路列車交路計劃時，應盡可能采用多交路多編組的靈活組織形式，節約企業變動成本，控制整個系統的總成本。

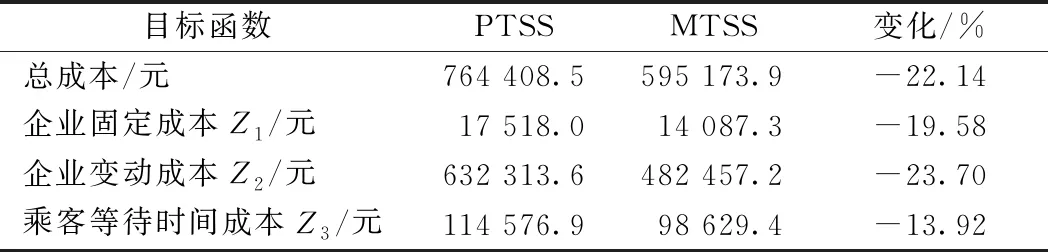
表7 目標值統計

綜上，本文所提出的優化方法可根據城市軌道交通線路的設施條件和客流特點，靈活設計多交路多編組的交路計劃，優于生產實踐中常用的經驗方法。盡管部分乘客在出行過程可能會經歷更多換乘，但從系統角度來看，模型所得出的MTSS不僅合理地設置了多交路使得線路的輸送能力與客流需求更加匹配，還更多地使用了小編組列車來提高區間列車開行頻率，從而有助于降低線路的運營企業成本和乘客的等待時間成本。

4.2.3 靈敏度分析

(1)列車交路數量

首先討論最大允許運行交路數量Ω對運營企業成本、乘客等待時間成本與列車平均滿載率的影響。根據前文結果，最優交路計劃包含4條交路。因此，固定其他參數，將Ω的取值分別設置為1～4，依次求解模型TSD3，結果見表8。其中，第2列，“1: 1-20, 19對6編”表示第1條交路的端點為車站1和20，且在該交路上開行19對6編組的列車。

表8 列車交路數量的影響

由表8可知，隨著交路數量Ω的增加，列車平均滿載率逐漸升高，總成本逐漸下降，其中，企業變動成本的下降對總成本下降的貢獻最大。另外，交路數量Ω由1條增加為2條時，總成本下降最為明顯，降幅為23.17%，隨后，交路數量Ω的進一步增加雖然能使總成本減少，但降幅較小。乘客等待時間成本在交路數量Ω為2時最高，隨著交路數量的繼續增加，乘客等待時間成本又逐漸下降，這是因為Ω從1增加為2時，開始出現乘客換乘，由此乘客等待時間成本明顯上升，但隨著Ω的繼續增加，模型TSD3能夠更加合理地設置交路，從而減少乘客換乘，降低乘客等待時間成本。因此，根據線路技術條件與客流特點，設置多交路可降低運營企業成本并控制乘客的等待時間成本。但同時，交路數量的增加也會使線路的運營復雜性與安全隱患增大[14]，建議運營部門結合線路運營水平進行多交路的設置。

(2)列車編組類型

現分析列車編組類型T對運營企業成本、乘客等待時間成本與列車平均滿載率的影響。可行列車編組T共設置6種情況：(1)僅使用6編組列車，T={6}；(2)僅使用8編組列車，T={8}；(3)可使用4編組或6編組列車，T={4,6}；(4)可使用4編組或8編組列車，T={4,8}；(5)可使用6編組或8編組列車，T={6,8}；(6)可使用4編組、6編組或8編組列車，T={4,6,8}。注意，僅使用4編組列車不能滿足客流需求，故不考慮。對這6種編組情況，最大允許運行交路數量Ω取為6，固定其他參數，分別求解模型TSD3，結果見表9。

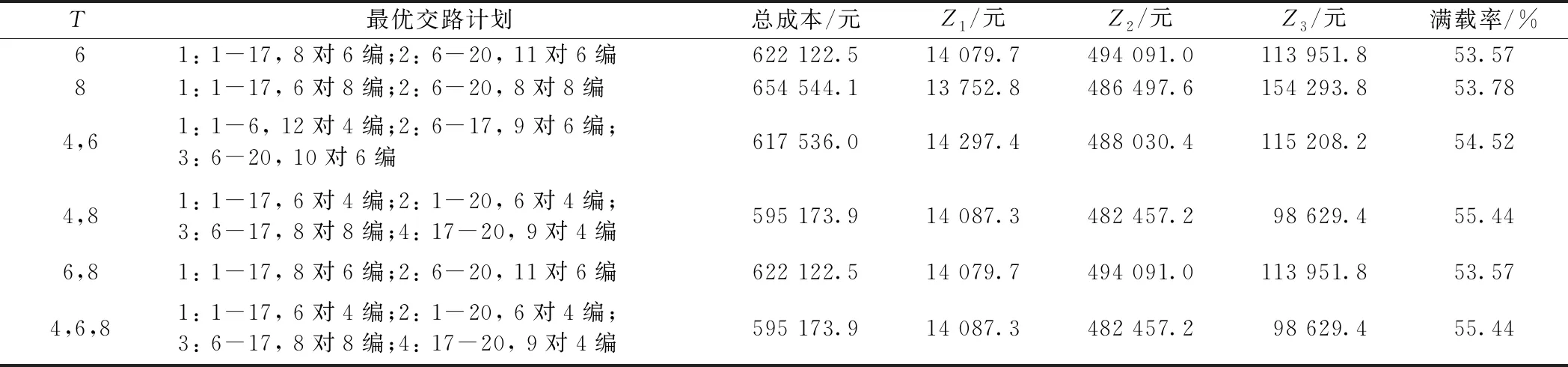
表9 列車編組類型的影響

由表9可知，當只采用一種編組的列車時，總成本高，特別是T={8}時，乘客等待時間成本明顯高于其他情況，導致其總成本最高，這是因為在相同客流條件下，列車編組越大，所需的列車開行對數就越低，乘客等待時間越長。在T={4,6,8}的情況下，總成本、企業變動成本與乘客等待時間成本最低，列車平均滿載率最高。需要指出的是，并不是可選的列車編組類型越多就一定會促使總成本越低，例如，表9中，T={4,6,8}與T={4,8}情況下的各項指標相同，T={6,8}與T={6}情況下的各項指標相同。但是，在可選的列車編組類型中加入小編組列車可有效降低總成本，例如，T={8}、T={6,8}與T={4,6,8}情況下的總成本逐漸降低，T={6}與T={4,6}情況下的總成本逐漸降低，原因在于在滿足客流需求的前提下，模型會盡量多地使用小編組列車提高各區間的列車開行對數，降低乘客的等待時間成本。因此，結合線路技術條件和客流特點，采用含小編組的多編組交路計劃可有效降低乘客等待時間成本，從而降低系統總成本。當然，為實施多編組交路計劃，需單獨采購小編組列車，還需配置更多工作人員，建議運營企業在進行技術經濟比選后考慮是否投入小編組列車。

5 結論

本文提出了具有多交路多編組運營條件的城市軌道交通線路列車交路設計問題的優化方法。首先，通過提前生成備選交路集構建服務網絡，并采用經典最優策略在服務網絡上進行客流分配，構建了多交路多編組列車交路設計的混合整數線性規劃模型。與既有研究相比，所提出模型可根據線路的技術條件和客流特點，靈活設計多交路多編組的列車交路計劃。同時，使用最優策略在所構建服務網絡上進行客流分配，描述乘客的出行過程，可更為準確地分析多交路對于乘客出行的影響。其次，根據乘客等待時間度量方法的特點，提出了服務網絡簡化方法來縮減模型規模，提高求解速度。計算結果表明，通過服務網絡簡化后的模型可快速求解典型城市軌道交通線路的列車交路設計問題，且其所得的多交路計劃優于生產實踐中常設計的基于經驗方法的單交路計劃。此外，若技術條件允許，運營企業應盡量設置多條交路，并在部分交路上適當開行小編組列車，以有效降低運營企業成本和乘客等待時間成本。

本文研究可在以下方面作進一步拓展。首先，下一步可將所提出方法應用于設計Y型城市軌道交通線路的多交路多編組列車交路計劃，并評估所提出模型和簡化方法的效果。其次，基于所構建的模型，研究含運營時段劃分和各時段交路設計的城市軌道交通線路全日行車計劃編制問題也是未來需要開展的工作。