任意角三分法

聶登科

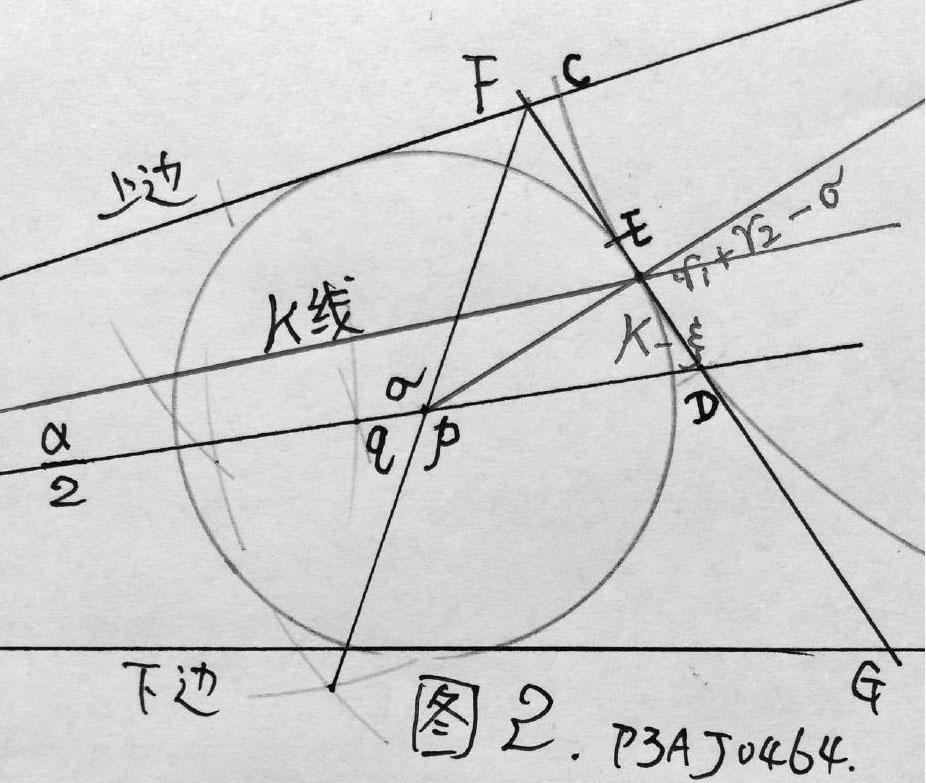
如圖所示，給定任意角α，頂點為O。若角度過大過小或位置不佳等，可通過雙倍縮放或旋轉，完成作業后恢復即可。

在任意一邊取任意一點A，并向另一邊作垂線，交點n。

平分角α，平分線交nA線B點。

以nA的長度為半徑r1，從A點出發，向角的另一邊作弧，交C點，交平分線上D點。

取弧CD的中點E，經過E、D兩點作直線交兩邊，分別為F、G。在△FOG中，作內切圓，得半徑r2，圓心為p。

以n為圓心，r1+r2為半徑，畫弧再交OB線為q。

再以q為圓心，作圓相切于弧ED。切點K即為三分點！

實際畫圖中，pq兩點難以區分，兩點間距是個無窮小量。理論上，前p心圓相切于弦ED，而非弧ED。后者才是K點！為紀念吾的出生地，本人命名它為K點（柯點）。

連接OK兩點，即得三分線，交于H。

說明：為圖面清晰，省略了部分作圖線。圖中未標記點、線、弧，為輔助作圖和或檢測之用。

如圖，按r1+r2作圓，退切至弧ED后，出現了該圓周超出了α的上下兩邊，并非真正的內切圓了。必須修減一個微量σ，σ為K點到弦ED的距離。而且是無休止修正，致使內切圓圓心沿著α的角平分線，在p、q兩點間q-σ段內，作無休止擺動，擺幅越來越小，直至無窮。同樣造成K點在D點方向與ξ之間作無休止擺動，擺幅越來越小，直至無窮。用1/3的小數表述，是一個小數點無窮位后的一個3而已。事實上當人們將兩顆心相連接時，K點已經確定，就是經過了無窮次修正的，無論作圖水平的高低，還是畫圖工具儀器的優劣，理論上它就是K點無疑。

隨著α角度的變化，σ和ξ的值也隨之不同。恕此不細述！

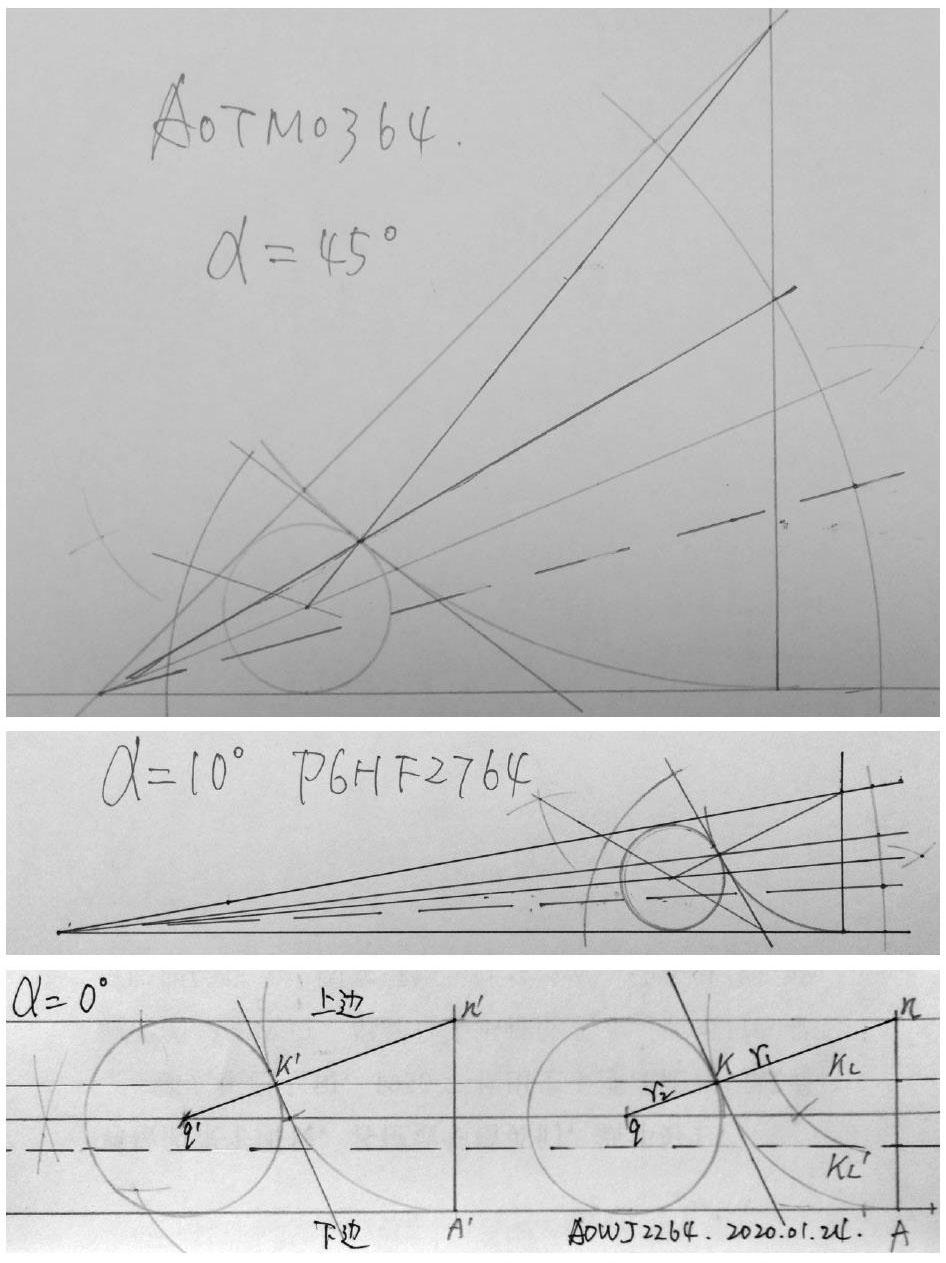
本三分法通用于任意角，通過鈍角銳化，旋轉縮放至最合適（10-45度）角域，五步（簡稱A、B、弧、圓、K）即刻完成。準確簡捷！

α角度越大，σ越小;α角度越小，σ越大。α角度過大，內切圓被壓縮進角尖，難以準確畫作內切圓，故須調整至合適的角域內操作，完成后調回。

當α=0°時，上下兩邊就成了兩條平行線。三分法依然成立，而且由此衍生出，該三分法可三等分任意兩條平行線間距。

如圖，以遠離頂點的小角度α角，依法畫作，所有的K點均在K線上。

姑且稱之為，弧圓切點法。

依法所作三分線，用幾何定理，三角公式皆可證明它的存在，證明該三分法科學。

角三分線就像平分線一樣，客觀存在，只不過之前沒有被發現而已。

由于本人沒有專業的制圖工具，且勉強在只能放置一張A4紙的桌面上操作，誤差較大。