基于溫室環境和作物生長的番茄基質栽培灌溉模型

徐立鴻，肖康俊，蔚瑞華

·農業生物環境與能源工程·

基于溫室環境和作物生長的番茄基質栽培灌溉模型

徐立鴻，肖康俊，蔚瑞華

（同濟大學電子與信息工程學院，上海 201804）

為解決涵蓋土壤蒸發和作物冠層蒸騰的土培作物蒸散模型不能直接應用于稻殼炭基質栽培番茄灌溉的問題，該研究首先通過修改Penman-Monteith模型的原始表達式來去除土壤蒸發部分，并引入TOMGRO模型來模擬番茄冠層生長，給出了阻抗參數的修正計算，得到了新的番茄基質栽培蒸騰模型。考慮到蒸騰模型中凈輻射項削弱了室外太陽輻射對冠層及以下部整株植株的耗水影響，進而將新的蒸騰模型與太陽輻射線性比例供水模型結合建立蒸騰－輻射綜合灌溉模型。結果表明，蒸騰－輻射綜合灌溉模型對上海崇明A8溫室番茄灌溉量的模擬結果與實際結果之間的相關系數高于0.95，平均相對誤差小于20%。這說明蒸騰－輻射綜合灌溉模型能夠較好地估算溫室稻殼炭基質栽培番茄的灌溉需水量，對深入研究溫室灌溉實施具有參考價值。

溫室；灌溉；番茄；基質栽培；Penman-Monteith模型；蒸騰作用

0 引 言

番茄是世界上最重要以及種植面積最廣泛的園藝作物[1]，同時也是中國農業生產過程中大面積種植且產量較高的蔬果之一[2]。無論大田種植還是溫室栽培，在整個生長周期中適宜的水分供給對番茄的生長發育起著至關重要的作用[3]。不合理的供水情況會對番茄生產效益產生不利影響；例如，供水過少會造成作物根系水分脅迫，而供水過多會造成根系供氧不足且會使得果實開裂或掉落[4]。在無土基質栽培中，由于基質蒸發較小且持水能力較弱，其水分控制對于防止作物水分脅迫非常重要，這就使得準確估算基質栽培作物的灌溉需水情況十分必要[5]。

在水文生態學中，作物需水量可與作物蒸散量（Evapotranspiration）互換使用，因而在無法準確測量該水文參數的情況下，估算作物蒸散量則是短期預測實際作物需水量的關鍵環節[6]。

聯合國糧食及農業組織（FAO）早于1998年以能量平衡和湍流傳導原理來修正Penman模型，提出了適用于大田作物需水量估算的Penman-Monteith蒸散模型，并且給出了以經驗作物系數將參考作物蒸散量轉換為實際蒸散量來反映作物實際水分需求的方式[7]。對于自然通風或不頻繁通風的日光溫室，由于室內空氣流通較為緩慢且風速幾乎為0，則會造成以作物幾何特征（零平面位移高度和粗糙度長度）和風速相關的對數函數直接計算的空氣動力阻抗趨于無限大。因此，在張培新等[8-9]修正空氣動力阻抗中風速項的基礎上，劉浩等[10]建立了一個需要日光溫室氣象數據和作物生長指標的溫室土培番茄蒸散量估算模型。更重要的是，在引入草基準面簡化Penman-Monteith模型原始表示過程中將葉片表層阻抗作為固定值，區別于這種經驗處理無法反映冠層葉片在不同生長階段受到太陽輻射影響而變化的情況，上述蒸散修正模型引入了Boulard等[11]提出的基于太陽輻射計算單葉氣孔阻力，以此來模擬葉片生長變化下受輻射影響的表層阻抗。

盡管許多研究依據實際溫室環境進行了阻抗參數的合理修正，使得Penman-Monteith蒸散模型適用于溫室土培作物冠層蒸騰量的估算，但這些修正模型在參數計算過程中并未將土壤蒸發部分從蒸散（包含了土壤蒸發和作物冠層蒸騰2個部分）中去除。然而，在西班牙東南部某塑料溫室開放基質栽培的模擬番茄蒸騰量的研究中，由于土壤被沙覆蓋層所覆蓋，PrHo模型（PrHo是一種可用作溫室蔬菜作物灌溉計劃決策支持系統的軟件，其中計算作物蒸散量的模型被稱作PrHo模型）所模擬的蒸散量被認為是土壤栽培蔬菜作物的蒸騰量[12-13]，這就意味著覆蓋土壤處理相當于移除土壤蒸發的影響。在無土栽培辣椒的有效灌溉研究中，Shin等[14]指出基質表面的蒸發很小甚至可以忽略不計。此外，在一些無土基質栽培作物的蒸騰量估算和灌溉管理的研究中[15-17]，“蒸騰”一詞用于反映作物的需水量，而非包含了土壤蒸發的“蒸散”。因而，在不考慮土壤蒸發量的情況下，利用Penman-Monteith參考蒸散模型及其修正模型來計算溫室有機基質栽培作物的冠層蒸騰量具有一定的挑戰性[3]。

在無土基質栽培的灌溉管理實踐中，傳統的灌溉方式是基于室外太陽輻射總量與作物蒸騰的線性比例關系來估算供水量[18]，類似的灌溉模型則是基于年內天數和當日輻射總量的線性表式[19]，而這些計算中忽略了白天時段光強變化引起水氣壓差變化對蒸騰速率的影響，尤其是在強光條件下估算作物實際需水量時會產生較大誤差[20]。因此，分別針對玫瑰和辣椒2種作物，Suay等[21-22]考慮了水汽壓差對作物蒸騰的影響，建立了溫室無土基質栽培作物蒸騰量估算的線性模型。然而，這種線性擬合輻射項與水氣壓差項的模型準確性是作物特異性的[23]，在很大程度取決于溫室小氣候環境，且在機理特性上未考慮阻抗參數對蒸騰表面水汽交換的影響。

灌溉作為溫室基質栽培作物水分供給的唯一來源，由于植物吸收和灌溉送水過程造成的額外損失，灌溉需求量始終大于作物需水量。值得注意的是，由于蒸騰模型中的凈輻射經過冠層葉面積指數截留，削弱了室外太陽輻射對冠層以下部分植株水分損失的影響，這就意味著在作物生長初期葉面積指數較小時，冠層截留凈輻射遠小于溫室透光后的太陽輻射。而在依據太陽輻射閾值觸發灌溉事件的溫室中，在葉面積指數小而太陽輻射強的情況下，僅使用蒸騰模型來估算整株植株需水量會嚴重低估灌溉需水量。為解決這一問題，本文在忽略土壤蒸發來修正Penman-Monteith模型得到番茄基質栽培蒸騰模型的基礎上，將其與太陽輻射線性供水模型結合使用多元線性回歸來建立蒸騰-輻射綜合灌溉模型，為溫室番茄基質栽培的灌溉需水量預測和實施規劃奠定基礎。

1 溫室番茄基質栽培場景介紹

本文的研究對象是位于上海崇明國家設施農業工程技術中心示范基地Venlo溫室（31°57'N, 121°70'E）的稻殼炭有機基質栽培的荷蘭小番茄（品種為Gorioso）。番茄的種植密度約為每平方米2.5株，在A8溫室中共有18個間隔1.5 m的種植列，每個種植列有23個間隔0.3 m的種植單位，每個種植單位有4個基質種植盒（0.15 m×0.15 m×0.1 m），分為2組，每組有2個緊密挨著的種植盒，每個種植盒配有1個滴箭，每2個種植盒中間另有1個滴箭，即每2株植株配有3個滴箭實施灌溉供水。采用輻射閾值觸發定量灌溉，即室外太陽輻射每累積100 J/cm2時使每個滴箭出水70 mL，廢液回收量由人工記錄。營養液的正常供給間隔為7～10 d，而在定植前期番茄根系吸收水分和養分能力較弱，在3～5 d澆施速效氮肥促進番茄植株營養生長。

番茄植株于每年9月20日定植，整個生長全周期約為300 d。移栽定植后平均每天植株增高5 cm，在定植約35～40 d后，番茄植株冠層高達2 m且葉面積指數達到最大值，經葉片修剪會維持在3.3～3.5 m2/m2范圍內。從定植到番茄成熟約為80 d，約每天可著色一個果實，平均8～10 d采摘一串果實，然后去掉果實下的2～3片葉片并卷起相應的莖干。每株植株大致保持18個莖節，每3個莖節有一串果實，即每株番茄保持6串果實，每串果實數控制在8個，單個成熟果實質量約為45 g，整個結果期每株番茄的總采摘量約為28～32串。

溫室內氣象站隨著番茄植株生長而受控向上移動，與植株冠層保持0.3 m的間距，可獲取室內空氣溫度、濕度和CO2濃度等數據；室外氣象站可獲取室外太陽輻射日累積量、降雨量和風速等數據。用于研究方法驗證分析的試驗數據來源于4 a番茄生長全周期的采集記錄，具體時間段為2014-09-20至2015-07-16、2015-09-20至2016-07-15(閏年)、2016-09-20至2017-07-16和2017-09-20至2018-07-16。

2 溫室番茄基質栽培灌溉模型的建立

2.1 Penman-Monteith蒸散模型及其局限性

估算作物的灌溉需水量取決于作物蒸散量的計算。依據能量平衡和湍流傳導，FAO給出了估算大田作物參考蒸散量的應用指導標準——Penman-Monteith蒸散模型，如式（1）所示。

式中ET0表示作物蒸散的潛熱通量，mm/d；=2.45為單位轉換系數，MJ/kg；為土壤熱通量，MJ/m2·d；R為凈輻射，是凈短波輻射R和凈長波輻射R的差值，MJ/m2·d；e為平均飽和水汽壓，e為實際水汽壓，kPa；D為水汽壓差與溫度曲線的斜率；r為空氣動力阻抗，s/m；r為表層阻抗，s/m；ρ為恒壓下的平均空氣密度，kg/m3；c為恒壓比熱，MJ/kg·℃；=0.054為干濕表常數，kPa·℃。

當日光溫室中的空氣流通較慢且風速近似為0時，空氣動力阻抗r的數值會趨于無限大，導致引入草基準面簡化參數得到的固定表層阻抗（70 s/m）和反照率為 0.23的Penman-Monteith模型一般式中水氣壓差近似為0。因此，為了使其能夠應用于不常通風的溫室中，研究學者通過修正空氣阻抗參數的風速項，得到了適用于溫室土培作物的參考蒸散模型，如式（2）所示。并且，在估算實際作物蒸散量時，作物系數K以FAO給定不同生長階段的推薦值（K在苗期為0.75，在開花期為1.05，在結實期為0.8）來轉換參考蒸散量。

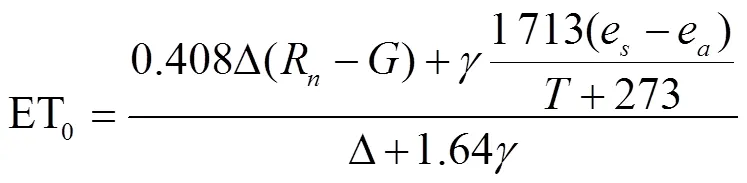
式中為溫室空氣日平均溫度，℃。

對于無土有機基質栽培作物，考慮到溫室基質栽培與土壤種植之間作物生長和蒸騰影響因素的明顯差異，應考慮從上述蒸散模型中去除土壤蒸發。

2.2 生長參數及阻抗修正

FAO指出，Penman-Monteith模型一般式是監測作物蒸散過程的物理和生理因素的簡單表示，主要取決于作物種植環境中的氣候條件；其引入作物系數以區分草基準面和實際作物之間的蒸散量，并不涉及作物實時生長，而是從蒸散量的歷史測量值與估計值的比值經驗得出。因此，本文將固定作物高度的草基準面替換為實際作物冠層蒸騰面，以葉面積指數實際變化來修正阻抗參數經驗表示，在無需引入作物系數的情況下直接計算作物蒸騰量。

2.2.1 基于番茄生長模型模擬葉面積指數

葉面積指數（Leaf Area Index，LAI）與實際作物表層阻抗r和到達作物冠層的截留凈輻射R相關。對于FAO引入固定作物高度的草基準面，Penman-Monteith模型一般式以經驗公式（LAI=24）來獲取葉面積指數，忽略了不同生長階段作物冠層葉片合理的生長變化。考慮引入番茄生長模型（Tomato Growth Model，TOMGRO）來模擬番茄冠層葉面積指數的實際變化，以便更為直觀地反映葉面積指數變化對冠層蒸騰的影響。

在實際溫室中，當葉面積指數達到允許最大值時會進行葉片修剪使得成熟到采收期間葉面積指數保持不變，這種溫室作物栽培特有的種植管理方式使得TOMGRO模型中葉面積指數LAI的增長模式通常以sigmoid函數形式表示[24]，如式（3）所示。

式中LAI為初始葉面積指數，m2/m2；LAImax為最大葉面積指數，m2/m2；兩者均為實際溫室中人工記錄。L= 35 000為葉片生長率滯后系數，L=4.1為葉片生長率。為主莖干上的莖節數（節），在該參數的計算表示中，TOMGRO模型假設單個作物生長最適溫度，用增減因子來模擬作物生長對室內氣溫的響應，其計算如下：

式中N=0.5，為最大莖節出現率，f()為溫度抑制函數，0()=2.5+0.025，1()=2.5-0.05，分別為作物生長率增長和衰減因子，NUM=1，為最大莖節生長率。

2.2.2 結合太陽輻射和葉面積指數修正表層阻抗

表層阻抗r描述的是水蒸氣從作物葉片內部飽和區域或蒸散面以下擴散到蒸散面本身的阻力，在簡化得到Penman-Monteith模型一般式時，其經驗表示結果（r≈70 s/m）為草基準面的單葉氣孔阻抗（r=100 s/m）與有效葉面積指數（LAI=0.5LAI）的比值。

然而，實際溫室有機基質栽培的番茄冠層蒸騰表面與大面積覆蓋地表的草基準面在蒸騰作用上存在較大差異，這就意味著將表層阻抗當作固定值并不足以反映基質栽培的番茄冠層葉片生長變化對蒸騰作用的影響。因此，考慮將番茄冠層模擬葉面積指數和與太陽輻射密切相關的氣孔阻力相結合，以獲得合理的表層阻抗計算方法。

對于溫室番茄，到達冠層的太陽輻射是影響葉片氣孔阻抗的最關鍵因素。Boulard等[11]給出了與草基準面的經驗公式不同的單葉氣孔阻抗r計算方式。

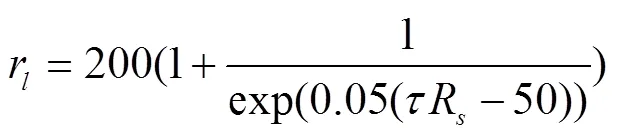
式中R為室外太陽輻射，MJ/m2·d；=0.65為崇明溫室透光率。在不考慮修剪葉片影響土壤覆蓋度的情況下，草基準面的經驗公式中有效葉面積指數由作物生長期的實際模擬葉面積指數表示，與受室外太陽輻射影響的單葉氣孔阻抗r相結合，可得到忽略了土壤蒸發影響的基質栽培番茄的新的表層阻抗r計算表示如下：

2.2.3 固定空氣動力阻抗

空氣動力阻抗r描述的是從零平面位移高度以上的距離向作物的有效表面傳遞動量的阻力。FAO指出，對于大范圍覆蓋地表的大田作物，必須考慮零平面位移高度和粗糙度長度等參數，而無土基質栽培環境下的高叢番茄則無需考慮這些與土壤蒸發相關的參數。

引入草基準面后，以2 m高的風速2簡化計算空氣動力阻抗，從其計算表示（r=208/2）不難發現，當不頻繁通風的日光溫室中空氣流通較為緩慢且風速2≈0時，空氣動力阻抗趨于無限大，這使得Penman-Monteith模型中的r/r≈0且水氣壓差接近于0，從而造成模型缺失作物蒸騰生理特性原理中所涵蓋的為從蒸騰表面去除水汽過程的提供動力的水氣壓差項，模型最終會退化成以太陽輻射為主要影響因素的線性模型。但是，這種由簡化計算表示和風速之間的極端關系所產生的一系列問題與實際情況相矛盾，因為實際溫室中的番茄作物生長在低風速情況下，仍會與小氣候環境之間存在水汽交換和熱量傳輸，并不會出現數學表示直觀反映的某項影響因素丟失的情況。

因此，本文在建立溫室番茄的基質栽培蒸騰模型過程中，考慮忽略與土壤蒸發相關的土壤覆蓋度、零平面位移高度和粗糙度長度的經驗計算影響，在封閉溫室或空氣流速緩慢的溫室中將新的空氣動力阻抗取為固定值（r=500 s/m），以簡化依據湍流傳導和熱傳遞原理推導的復雜計算表示。針對上述處理，通過敏感性分析驗證了空氣動力阻抗在可能取值范圍內變化對蒸騰量模擬結果影響較小而作為固定值的合理性，并且在Wang等[25]的相關研究中也明確表示在封閉溫室或低氣流低風速溫室中，將其看作是一個固定值是合理的。

2.3 基質栽培番茄蒸騰模型

經過上述推導和修正過程可以看出，輻射項和對流項仍被保留以反映作物蒸騰生理特性，并且考慮與作物冠層蒸騰表面水汽交換直接相關的阻抗參數的修正計算，根據實際溫室有機基質栽培環境來去除土壤蒸發的影響，并以實際作物冠層蒸騰表面的生長變化來修正相關參數的經驗計算公式，得到最終適用于溫室稻殼炭有機基質栽培場景的番茄蒸騰模型表示如下：

式中Tr為溫室基質栽培番茄蒸騰量，mm/d；C=86 400/ 1.01=4.79×105為計算系數， =0.62為水蒸氣與干空氣的分子量比，0.287為比氣體常數；VPD=e?e為水汽壓差，kPa；R=R(1exp(·LAI))為番茄冠層截留凈輻射，MJ/m2·d；在冠層截留凈輻射的計算中，=0.8為番茄消光系數，LAI為TOMGRO模型模擬的冠層葉面積指數；r=500 s/m為新的蒸騰模型中固定空氣動力阻抗表示；r為新的蒸騰模型中冠層表層阻抗表示。

2.4 溫室基質栽培番茄蒸騰-輻射綜合灌溉模型

由番茄基質栽培蒸騰模型輻射項中截留凈輻射R的計算表示可知，到達作物冠層經過葉面積指數截留的凈輻射遠小于溫室透光后的太陽輻射，這就削弱了實際太陽輻射對番茄整株植株蒸騰的影響。在移栽定植約35～40 d后，番茄植株冠層高達2 m且葉面積指數維持在3.3～3.5 m2/m2范圍內，這就導致溫室透光后的太陽輻射在株間分布不均衡，番茄基質栽培蒸騰模型在很大程上用于反映作物冠層蒸騰變化，而不能較為準確地反映整株植株冠層及其以下部分的所有葉片蒸騰耗水情況。

此外，由于溫室灌溉方式的不同，在生長初期葉面積指數較小造成截留凈輻射較小時，強烈的太陽輻射使得溫室灌溉用水供給量要遠高于蒸騰模型估算的作物需水量。這主要是因為蒸騰模型中所引入的番茄生長變化僅針對冠層蒸騰表面而言，較小的葉面積指數使得冠層覆蓋度小，而冠層以下部分的耗水情況未被蒸騰模型考慮進去。針對上述問題，需要在反映番茄冠層耗水的基質栽培蒸騰模型的基礎上，額外考慮太陽輻射對冠層以下部分耗水的影響，建立蒸騰-輻射綜合灌溉模型來模擬番茄整株植株的灌溉需水情況。

由于新建立的番茄基質栽培蒸騰模型和太陽輻射線性供水模型的表示形式均已確定，它們在灌溉模型相關研究中均被以經驗比例系數線性轉換為灌溉量，因而考慮以番茄基質栽培蒸騰模型和太陽輻射線性供水模型作為二元自變量以及模擬灌溉量作為因變量來建立帶有偏置項的多元線性回歸[26-27]灌溉模型，其表示如下：

式中I為蒸騰-輻射綜合灌溉模型模擬灌溉需水量，mm/d；Tr為新建立的番茄基質栽培蒸騰模型模擬冠層蒸騰量，mm/d；I=τR/λ為太陽輻射線性供水模型模擬作物耗水量，mm/d；ω和ω分別表示番茄基質栽培蒸騰模型和太陽輻射線性供水模型的權重系數，ω為偏置項回歸系數。

SPSS軟件[28]被用于求解溫室基質栽培番茄的蒸騰-輻射綜合灌溉模型的各個權重系數，以及驗證建立蒸騰-輻射綜合灌溉模型是否可以滿足使用多元線性回歸的約束條件，即試驗數據樣本殘差需要服從或近似為正態分布。

為了確保使用多元線性回歸建立的溫室基質栽培番茄蒸騰-輻射綜合灌溉模型具有一定的合理性，并能較好地估算其他年份的灌溉需水量，這就需要足夠的數據樣本進行訓練支撐。基于現有試驗數據用于訓練和驗證的樣本量不足，本文在現有數據樣本基礎上加入適當的高斯噪聲來形成新的樣本數據，以達到合理擴充樣本的目的。

以灌溉用水量數據為例，所加入的擾動表示為0均值且方差為0.3的高斯噪聲，以此反映實驗溫室人工記錄排液量來獲取實際灌溉消耗所允許的誤差值。經過隨機高斯采樣對現有數據產生干擾后，用于多元線性回歸的樣本數據量從4個全周期數據擴展了一倍。以6個番茄生長全周期（2014-09-20至2015-07-16和2015-09-20至2016-07-15的原始數據以及在4個全周期原始數據基礎上加入高斯噪聲后的新數據）作為訓練樣本，可得到蒸騰-輻射綜合灌溉模型的回歸系數；并以余下2個全周期（2016-09-20至2017-07-16和2017-09-20至2018-07-16）的原始數據作為測試樣本，來驗證多元線性回歸模型估算溫室稻殼炭基質栽培的番茄灌溉量的準確性。

在試驗樣本數據擴充后，使用SPSS軟件對訓練輸入（番茄基質栽培蒸騰模型模擬冠層蒸騰量和太陽輻射線性供水模型模擬作物耗水量）和訓練輸出（實際灌溉量）進行線性回歸擬合，可得到蒸騰-輻射綜合灌溉模型的回歸系數分別為ω=0.412，ω=0.706，ω=0.338，則溫室稻殼炭基質栽培番茄的蒸騰-輻射綜合灌溉模型的具體表示如下：

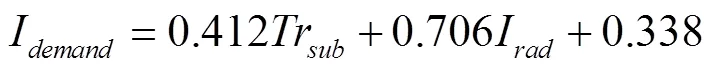
此外，SPSS軟件線性擬合得到的蒸騰-輻射綜合灌溉模型的擬合精度為R2=0.916；并且它還驗證了使用多元線性回歸建立灌溉模型是否滿足約束條件——樣本殘差近似或服從正態分布，樣本標準殘差的直方圖和正態P-P圖驗證結果如圖1所示。

由圖1可知，樣本標準殘差的均值（Mean=6.94E-15）近似為0，且在直方圖分布形式上近似為0均值且方差（Std.Dev.=0.999）約為1的正態分布，而正態P-P圖也顯示了偏差的期望累積概率和與預測累積概率大致相同，大部分點都位于直線上，只有少部分點小距離偏離直線。這進一步驗證了用于求解模型擬合系數的試驗數據在引入高斯噪聲擴充樣本的情況下，數據量達到了偏差服從正態分布的約束條件，這表明使用多元線性回歸建立的蒸騰-輻射綜合灌溉模型具有一定的合理性。

3 結果與分析

3.1 溫室土培蒸散模型與基質栽培蒸騰模型的對比

為了驗證本文所建立的溫室番茄基質栽培蒸騰模型修正的合理性，以及相比于溫室土培作物蒸散模型應用于無土基質栽培場景估算的準確性，對比分析了這2種模型模擬番茄蒸騰量的結果，如圖2所示。驗證分析所使用的試驗數據來源于上海崇明A8溫室4 a采集記錄的番茄生長全周期300 d的氣象數據、TOMGRO模型模擬生長參數數據和實際蒸騰量數據；4個番茄生長全周期的具體時間段為2014-09-20至2015-07-16、2015-09-20至2016-07-15(閏年)、2016-09-20至2017-07-16和2017-09-20至2018-07-16。

從圖2中可以看出，土培作物蒸散模型與番茄基質栽培蒸騰模型模擬蒸騰量的變化趨勢非常接近，主要是因為2個模型都是在Penman-Monteith蒸散模型原始表示的基礎上依據栽培環境進行簡化和修正的；而且作為影響番茄蒸騰能量供應的主要因素，室外太陽輻射使得2種模型的模擬蒸騰量與凈輻射之間高度相關。依據溫室土壤栽培環境修正的Penman-Monteith蒸散模型高估了作物蒸騰量，而且比番茄基質栽培蒸騰模型具有更高的模擬值，這與其他研究學者[29-31]的試驗結果相似。造成這種現象的原因是由于Penman-Monteith蒸散模型主要是針對室外大田種植環境下農作物的灌溉指導而建立的，而露天土壤種植作物受到土壤蒸發和額外降水供應對蒸散過程的影響，基質栽培和土壤種植之間的生長環境和水分補給方式的差異導致了作物蒸騰量的估算存在明顯差距。

此外，由圖2中顯示的模擬番茄蒸騰量的對比可以看出，約25 d內的模型模擬蒸騰量與實際蒸騰量的數值較為相近，這主要是由于生長初期番茄冠層葉面積指數較小，在凈輻射的計算中對溫室透光后的太陽輻射截留的影響較小，使得作物蒸騰量的模擬值與實際值都很小，這符合葉面積指數與潛在蒸騰速率成正比相關的認知。而在番茄摘果后期（距離摘果結束約50～60 d），由于每次摘果后修剪該果實下2～3片葉片和干枯莖干，直至一株番茄6串果實完全采摘，該階段的葉面積指數會相應減小，這與生長初期葉面積指數較小的情況類似，會使得2種模型模擬蒸騰量的結果與實際蒸騰量均較為相近，模擬誤差相對變小。

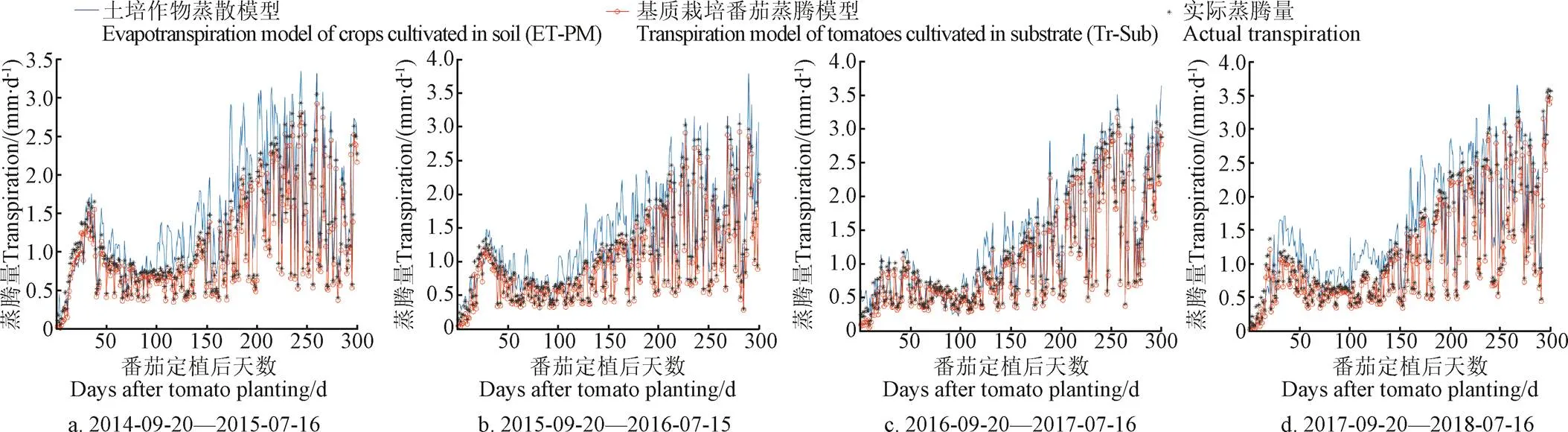
圖2　2種模型（ET-PM和Tr-Sub）在不同年份的模擬蒸騰量與實際蒸騰量的比較

表1給出了溫室土培作物蒸散模型和番茄基質栽培蒸騰模型模擬蒸騰量分別與實際蒸騰量之間的相關系數和誤差結果，由表1可以看出，與土培作物蒸散模型相比，番茄基質栽培蒸騰模型模擬番茄蒸騰量具有更小的誤差，其與實際蒸騰量的相關系數大于0.95，平均絕對誤差小于0.1 mm/d、平均相對誤差小于10%，均方根誤差小于0.1，且均比土培作物蒸散模型的模擬誤差小2倍以上。這表明，在估算溫室稻殼炭有機基質栽培的番茄蒸騰量時，依據Penman-Monteith蒸散模型修正得到的番茄基質栽培蒸騰模型具有較高的準確性。并且，相比于土培作物蒸散模型以經驗作物系數來反映草基準面和實際作物蒸散面之間的生長差異，番茄基質栽培蒸騰模型通過模擬番茄冠層蒸騰表面的葉片實時生長變化，在保留了作物蒸騰機理特性的同時，從蒸散中消除土壤蒸發的影響以此來反映在土培作物蒸散和基質栽培作物蒸騰之間的差異是合理的。

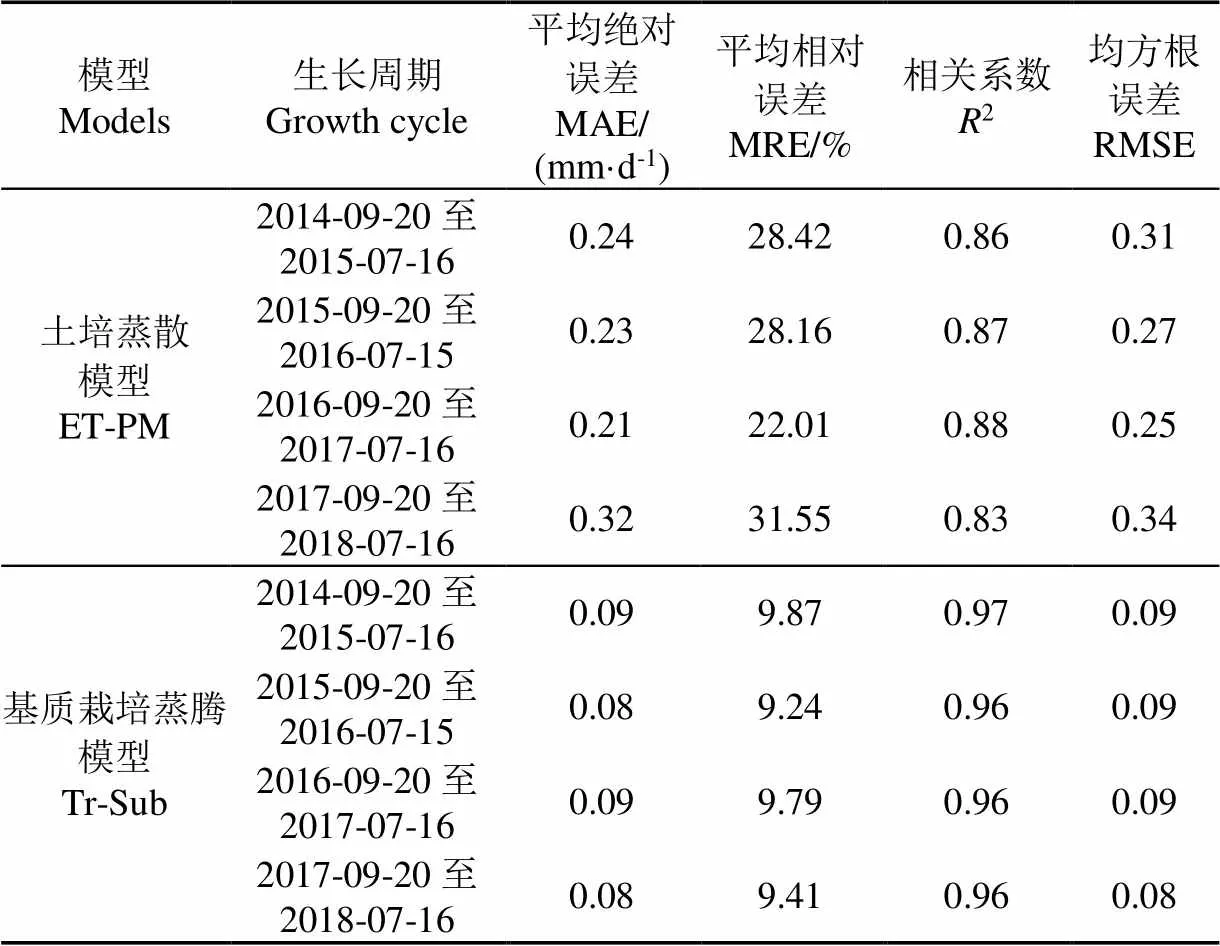
表1 2種模型模擬蒸騰量與實際蒸騰量的相關系數和誤差結果

3.2 蒸騰-輻射綜合灌溉模型模擬灌溉量與實際灌溉量的對比分析

為了進一步驗證使用多元線性回歸方法建立的蒸騰-輻射綜合灌溉模型模擬番茄灌溉需水量的準確性，使用保留的2個全周期內（2016-09-20至2015-07-16和2017-09-20至2018-07-16）的原始數據對灌溉模型進行了仿真模擬，并與實際灌溉量數據進行對比分析，如圖3所示。

圖3 蒸騰-輻射綜合灌溉模型模擬灌溉量與實際灌溉量的比較

由于番茄生長初期葉面積指數較小，蒸騰模型中參與計算的冠層截留凈輻射嚴重削弱了室外太陽輻射的實際影響，使得估算蒸騰量較小；而從圖3中可以看出，番茄生長初期的灌溉量并非與蒸騰量直接相關，這也就意味著在基質栽培番茄蒸騰模型的基礎上附加考慮室外太陽輻射的影響來建立綜合灌溉模型是有必要的。一方面，基質栽培番茄蒸騰模型考慮了溫室小氣候環境變化、作物實時生長變化和冠層截留凈輻射對作物耗水的綜合影響；另一方面，額外考慮室外太陽輻射的影響，以補償其在不同生長階段冠層葉片截留下受到不同程度的削弱，兩者結合則能更好地反映影響番茄耗水的因素。

由圖3可知，2017-09-20至2018-07-16的生長全周期內出現了少數情況（2017-09-24、2017-10-01、2017-10-02和2018-06-25）的模擬灌溉量與實際灌溉量之間存在較大偏差，而絕大部分模擬灌溉需水量變化趨勢上與實際灌溉量基本一致且數值上的誤差較小。此外，圖3中顯示在灌溉量數值較大時，模擬值與實際值較為相近；而在灌溉量數值較小時，兩者存在一定誤差，這主要是因為灌溉模型在蒸騰項和輻射項的數值較小時，偏差項的存在對模型估算結果產生了主導影響。為了更精確地分析蒸騰-輻射灌溉模型估算有機基質栽培番茄的灌溉需水量的總體準確性，表2給出了蒸騰-輻射綜合灌溉模型模擬灌溉量與實際灌溉量之間的誤差結果以及相關系數。

由表2可以看出，2個生長全周期的模擬灌溉量與實際灌溉量之間的平均相對誤差均小于20%，平均絕對誤差均小于0.29 mm/d且均方根誤差也都不大于0.3，這些誤差數值也都小于擴充試驗數據所使用的高斯噪聲的方差，也就是崇明溫室人工記錄灌溉相關數據所允許的誤差0.3 mm/d，且表中的決定系數均高于0.95。因此，基于多元線性回歸建立蒸騰-輻射綜合灌溉模型具有一定的合理性，且能夠較為準確地預測溫室稻殼炭有機基質栽培番茄的灌溉需水量。

表2 實際灌溉量與模擬灌溉量的決定系數和誤差分析結果

3.3 葉面積指數與空氣動力阻抗的敏感性分析

模型參數的敏感性分析是指其他參數保持不變的情況下，模型中某一參數的變化幅度對結果的影響程度。為了驗證有機基質栽培番茄蒸騰模型中將空氣動力阻抗r作為固定值的合理性，以及考慮冠層蒸發面葉面積指數LAI反映實際作物生長情況的必要性，針對這2個參數使用SimLab軟件中FAST方法作了局部敏感性分析，分析參數r在對數函數表示中風速2變化范圍0.05～1.0 m/s內其值變化以及參數LAI在LAI～LAImax范圍變化分別對測試期間有機基質栽培番茄蒸騰模型模擬值的影響。

表3 葉面積指數與空氣動力阻抗的敏感度

一階敏感性指數反映的是參數對模型輸出總方差的直接貢獻率，總敏感性指數反映了參數直接貢獻率和通過與其他參數的交互耦合作用間接對模型輸出總方差的貢獻之和。

從表3中可以看出，參數r的一階敏感性指數和總敏感性指數均小于0.1，這表明該參數對模擬結果影響較小，將其作為固定值較為合理；而參數LAI的敏感性指數遠大于0.1，這表明該參數對模擬結果影響非常大，其主要原因是蒸騰模型中考慮室外太陽輻射到達作物冠層的截留凈輻射與葉面積指數緊密相關，因而根據作物冠層蒸騰面的實際生長情況模擬葉面積指數是有必要的。

4 結 論

為解決溫室土培作物蒸散模型不能直接適用于溫室稻殼炭基質栽培番茄灌溉的問題，本研究基于作物蒸散機理特性去除土壤蒸發的影響，首先建立了溫室基質栽培番茄蒸騰模型。選取了上海崇明A8溫室番茄4個生長全周期采集記錄的試驗數據進行仿真，由仿真結果可以看出，溫室土培作物蒸散模型過高估計番茄蒸騰量，而溫室基質栽培番茄蒸騰模型模擬番茄蒸騰量具有更小的誤差，其與實際蒸騰量的平均絕對誤差小于0.1 mm/d、平均相對誤差小于10%和均方根誤差小于0.1，且均比溫室土培作物蒸散模型的模擬誤差小2倍以上，因而更適合于不考慮土壤蒸發的基質栽培番茄蒸騰量估算。

然后，考慮到基質栽培番茄蒸騰模型中凈輻射經過冠層葉片截留后削弱了室外太陽輻射對冠層及以下部分整株植株的耗水影響，本研究在基質栽培番茄蒸騰模型的基礎上額外考慮了太陽輻射對整個番茄植株耗水量的影響，并使用多元線性回歸建立了蒸騰-輻射綜合灌溉模型。以番茄2個生長全周期內（2016-09-20至2015-07-16和2017-09-20至2018-07-16）的試驗數據對蒸騰-輻射綜合灌溉模型進行模擬精度測試，由仿真結果可以看出，模擬灌溉量與實際灌溉量之間的平均相對誤差小于20%，平均絕對誤差小于0.29 mm/d且均方根誤差不大于0.3，這些誤差數值也都小于崇明溫室人工記錄灌溉相關數據所允許的誤差。因此，蒸騰-輻射綜合灌溉模型在整個生長期內對番茄灌溉需水量的估算具有較高精度，且模型參數的獲取和仿真估算過程相對簡單。

綜上所述，蒸騰-輻射綜合灌溉模型在反映番茄耗水情況受到溫室小氣候環境、室外太陽輻射和作物生長變化的綜合影響上具有一定的優勢，可以作為有效估算溫室稻殼炭有機基質栽培番茄的灌溉消耗的一種方法，并能為溫室精準灌溉控制提供模型支撐。

[1]Fernqvist F. Consumer Experiences of Tomato Quality and the Effects of Credence[D]. Uppsala: Swedish University of Agricultural Sciences, 2014.

[2]孫婧，田永強，高麗紅，等. 秸稈生物反應堆與菌肥對溫室番茄土壤微環境的影響[J]. 農業工程學報，2014，30(6)：153-164.

Sun Jing, Tian Yongqiang, Gao Lihong, et al. Effects of straw biological reactor and microbial agents on physicochemical properties and microbial diversity of tomato soil in solar greenhouse[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(6): 153-164. (in Chinese with English abstract)

[3]Nam D S, Moon T, Lee J W, et al. Estimating transpiration rates of hydroponically-grown paprika via an artificial neural network using aerial and root-zone environments and growth factors in greenhouses[J]. Horticulture, Environment and Biotechnology, 2019, 60: 913-923.

[4]Sezen S M, Yazar A, Tekin S. Physiological response of red pepper to different irrigation regimes under drip irrigation in the Mediterranean region of Turkey[J]. Scientia Horticulturae, 2019, 245: 280-288.

[5]Barrett G E, Alexander P D, Robinson J S, et al. Achieving environmentally sustainable growing media for soilless plant cultivation systems: A review[J]. Scientia Horticulturae, 2016, 212: 220-234.

[6]Shiri J, Landeras G, Nazemi A H, et al. Daily reference evapotranspiration modeling by using genetic programming approach in the Basque Country (Northern Spain)[J]. Journal of Hydrology, 2012, 414(2): 302-316.

[7]Allen R G, Pereira L S, Raes D, et al. Crop evapotranspiration: Guidelines for computing crop water requirements[M]. Rome: Irrigation and Drainage Paper No 56, 1998.

[8]張培新，賀超興，張志斌，等. 基于生理發育時間的日光溫室番茄發育模擬模型[J]. 中國農業氣象，2006，27(4)：314-317.

Zhang Peixin, He Chaoxing, Zhang Zhibin, et al. A simulation model for tomato plant growth and development in solar greenhouse based on physiological development time[J]. Chinese Journal of Agrometeorology, 2006, 27(4): 314-317. (in Chinese with English abstract)

[9]王健，蔡煥杰，李紅星，等. 日光溫室作物蒸發蒸騰量的計算方法研究及其評價[J]. 灌溉排水學報，2006，25(6)：11-14.

Wang Jian, Cai Huanjie, Li Hongxing, et al. Study and evaluation of the calculation methods of reference crop evapotranspiration in solar-heated greenhouse[J]. Journal of Irrigation and Drainage, 2006, 25(6): 11-14. (in Chinese with English abstract)

[10]劉浩，段愛旺，孫景生，等. 基于Penman-Monteith方程的日光溫室番茄蒸騰量估算模型[J]. 農業工程學報，2011，27(9)：208-213.

Liu Hao, Duan Aiwang, Sun Jingsheng, et al. Estimating model of transpiration for greenhouse tomato based on Penman-Monteith equation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(9): 208-213. (in Chinese with English abstract)

[11]Boulard T, Wang S. Greenhouse crop transpiration simulation from external climate conditions[J]. Agricultural and Forest Meteorology, 2000, 100(1): 0-34.

[12]Castilla N, Hernández J. The plastic greenhouse industry of Spain[J]. Chron Hort, 2005, 45(3): 15-20.

[13]Gallardo M, Thompson R B, Rodríguez J S, et al. Simulation of transpiration, drainage, N uptake, nitrate leaching, and N uptake concentration in tomato grown in open substrate[J]. Agricultural Water Management, 2009, 96(12): 1773-1784.

[14]Shin J H, Park J S, Son J E. Estimating the actual transpiration rate with compensated levels of accumulated radiation for the efficient irrigation of soilless cultures of paprika plants[J]. Agricultural Water Management, 2014, 135(2): 9-18.

[15]Tai N H, Park J S, Shin J H, et al. Analyses of transpiration and growth of paprika (L.) as affected by moisture content of growing medium in rockwool culture[J]. Korean Journal of Horticultural Science and Technology, 2014, 32(3): 340-345.

[16]Salcedo G A, Reca J, Pérez-Sáiz M, et al. Irrigation water consumption modelling of a soilless cucumber crop under specific greenhouse conditions in a humid tropical climate[J]. Ciência Rural, 2017, 47(2): 1-10.

[17]Nikolaou G, Neocleous D, Katsoulas N, et al. Modelling transpiration of soilless greenhouse cucumber and its relationship with leaf temperature in a mediterranean climate[J]. Emirates Journal of Food and Agriculture, 2017, 29(12): 911-920.

[18]Rouphael Y, Colla G. Modelling the transpiration of a greenhouse zucchini crop grown under a Mediterranean climate using the Penman-Monteith equation and its simplified version[J]. Crop & Pasture Science, 2004, 55(9): 931-937.

[19]Baille M, Baille A, Laury J C. A simplified model for predicting evapotranspiration rate of nine ornamental species vs. climate factors and leaf area [J]. Scientia Horticulturae (Amsterdam), 1994, 59(3/4): 217-232.

[20]Shin J H, Son J E. Application of a modified irrigation method using compensated radiation integral, substrate moisture content, and electrical conductivity for soilless cultures of paprika[J]. Scientia Horticulturae, 2016, 198: 170-175.

[21]Suay R, Martinez P F, Roca D, et al. Measurement and estimation of transpiration of a soilless rose crop and application to irrigation management[J]. Inverse Problems, 2003, 614: 409-433.

[22]Ta T H, Shin J H, Ahn T I, et al. Modeling of transpiration of paprika (L.) plants based on radiation and leaf area index in soilless culture[J]. Horticulture Environment and Biotechnology, 2011, 52(3): 265-269.

[23]Fazlil-Ilahil W F. Evapotranspiration Models in Greenhouse[D]. Wageningen: Wageningen Agricultural University, 2009.

[24]Bacci L, Battista P, Rapi B. Evaluation and adaptation of TOMGRO model to Italian tomato protected crops[J]. New Zealand Journal of Crop & Horticultural Science, 2012, 40(2): 115-126.

[25]Wang S, Boulard T, Haxaire R. Air speed profiles in a naturally ventilated greenhouse with a tomato crop[J]. Agricultural and Forest Meteorology, 1999, 96(4): 181-188.

[26]Bianco V, Manca O, Nardini S. Electricity consumption forecasting in Italy using linear regression models[J]. Energy, 2009, 34(9): 1413-1421.

[27]Hu T, Wang T, Li J, et al. Binary linear regression and statistical learning of behavior model for human teleoperator [C]//IEEE International Conference on Mechatronics & Automation. IEEE, 2016.

[28]Waghmare S N, Sakhale C N. Formulation of experimental data based model using SPSS (Linear Regression) for stirrup making operation by human powered flywheel motor[J]. International Research Journal of Engineering and Technology (IRJET), 2015, 4(2): 461-468.

[29]Prenger J J, Fynn R P, Hansen R C. A comparison of four evapotranspiration models in a greenhouse environment[J]. Transactions of theAmerican Society of Agricultural Engineers, 2002, 45(6): 1779-1788.

[30]Villarreal-Guerrero F, Kacira M, Fitz-Rodríguez E, et al. Comparison of three evapotranspiration models for a greenhouse cooling strategy with natural ventilation and variable high pressure fogging[J]. Scientia Horticulturae, 2012, 134: 210-221.

[31]López-Cruz I L, Olivera-López M, Herrera-Ruiz G. Simulation of greenhouse tomato crop transpiration by two theoretical models[J]. Acta Horticulturae, 2008, 797: 145-150.

Irrigation models for the tomatoes cultivated in organic substrate based on greenhouse environment and crop growth

Xu Lihong, Xiao Kangjun, Wei Ruihua

(201804,)

Water supply is an essential to the normal growth of plants, due to too much or insufficient water can seriously confine the yield and quality of greenhouse crops. The traditional greenhouse irrigation method mainly triggers quantitative irrigation system through timing control and radiation thresholds, without considering the comprehensive impact of microclimate changes on water consumption of crops in the greenhouse environment. In the conventional model, such as converting crop transpiration to irrigation water demand with the empirical ratio factor, there is a lacking the fact that the growth of crop canopy leaves can weaken the effect of solar radiation on water consumption of plants below the canopy. The conventional water supply methods cannot meet the actual needs of crops, and thereby inevitably cause serious waste of water resources and environmental pollution by excessive discharge of nutrient solution waste liquid, eventually deteriorate the economic benefit of crop production in greenhouse. Therefore, it is of great practical value to establish an irrigation model based on crop transpiration physiological characteristics and intercepted radiation effects of actual canopy growth changes. The relevant research of the soilless substrate cultivation crop transpiration model pointed out that the surface evaporation of the substrate can be small or even negligible, indicating that the soil evaporation does not need to be considered when estimating the tomato transpiration of the soilless substrate cultivation. Penman-Monteith evapotranspiration model including soil evaporation cannot accurately estimate the transpiration of substrate-cultivated tomato in terms of greenhouse. In addition, some models were introduced a grass datum with a fixed crop height and a large area covering the ground, in order to empirically simplify the calculation of impedance parameters, and then used historical data to fit crop coefficient as a medium for converting reference evapotranspiration to actual evapotranspiration. However, the estimation process did not consider the actual growth of the crop evapotranspiration surface. In this study, a new transpiration model was established for the tomato plants cultivated on rice-husk charcoal substrate in the greenhouse. The calculation of empirical parameters was modified based on soil evaporation in the original representation of the evapotranspiration model, according to the distinction between soil-cultivated crop evapotranspiration and substrate-cultivated crop transpiration. TOMGRO model was introduced to simulate real-time growth changes of tomatoes to replace the grass datum of fixed growth parameters. The new transpiration model has added the resistance parameters of the water vapor exchange between the leaves and outside air, while maintaining the characteristics of crop transpiration, indicating more suitable for the greenhouse microclimate environment and the real-time growth of crops. In the simulated transpiration results of historical data from each full cycle of tomato growth in four years, compared with the greenhouse soil-cultivated crop evapotranspiration model, the transpiration model of substrate tomato shows a small error to simulate tomato transpiration, where the average absolute error are less than 0.1 mm/d, the average relative error are less than 10%, the root mean square error are less than 0.1 and the correlation coefficient are greater than 0.95. Considering that due to the net radiation interception weakening solar radiation, the transpiration model of substrate tomato can be used to describe the transpiration changes of crop canopy, but ignore the water consumption of the entire plant canopy and below. Therefore, a transpiration-radiation integrated irrigation model was established by multiple linear regression method, where introducing the solar radiation linear water supply model as a linear compensation to estimate the tomato irrigation water requirement using the substrate tomato transpiration model. Comparing the actual irrigation data, the average absolute error of the simulated irrigation volume are less than 0.29 mm/d, the average relative error are less than 20%, and the root mean square error are no more than 0.3. These errors are also less than the allowable error 0.3 mm/d of manual recording irrigation data in the experimental greenhouse. The estimation of greenhouse tomato water consumption in substrate cultivation scenario, transpiration-radiation integrated irrigation model have high accuracy, certain rationality and practicability. These models can provide a theoretical basis for the prediction of irrigation water consumption of rice-husk charcoal substrate cultivated tomato in the greenhouse and irrigation implementation plan.

greenhouse; irrigation; tomato; substrate cultivation; Penman-Monteith model; crop transpiration

徐立鴻，肖康俊，蔚瑞華. 基于溫室環境和作物生長的番茄基質栽培灌溉模型[J]. 農業工程學報，2020，36(10)：189-196.doi：10.11975/j.issn.1002-6819.2020.10.023 http://www.tcsae.org

Xu Lihong, Xiao Kangjun, Wei Ruihua. Irrigation models for the tomatoes cultivated in organic substrate based on greenhouse environment and crop growth[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(10): 189-196. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2020.10.023 http://www.tcsae.org

2020-04-13

2020-05-10

上海市科技興農重點攻關項目（滬農科創字（2018）第3-2號）；上海市科委創新行動計劃項目（17391900900）

徐立鴻，教授，博士生導師，主要從事溫室環境建模與控制、預測控制和智能控制研究。Email：xulihong@tongji.edu.cn

10.11975/j.issn.1002-6819.2020.10.023

S271

A

1002-6819(2020)-10-0189-08