計及供電可靠性的多目標分布式電源選址定容方法

蓋克勝，陳煥浩

(國網江西省電力有限公司吉安供電分公司，江西吉安343000)

0 引言

分布式電源在配電網中的滲透率日趨提高,給配電網的供電可靠性、電能質量等均造成不利的影響[1-2],這種影響的程度與分布式電源 (DG)接入位置及接入容量密切相關。設計多目標的DG選址定容方法,優化化DG接入位置和容量,同時提高分布式電源和配電網運行的安全性、可靠性和經濟性已成為當前共同關注的熱點[3-4]。

目前選址定容方法所考慮的優化目標可分為兩類,即經濟性相關和可靠性相關的目標[5]。文獻[6]對比了分布式電源接入前后配電網網損的變化,采用基于模擬退火算法的改進粒子群算法求解以網損最小為目標的分布式電源接入優化模型,但并未考慮分布式電源接入對配電網可靠性的影響。文獻 [7-8]的分布式電源接入優化模型綜合考慮了配電網網損、電壓偏差及靜態電壓穩定裕度,采用多種群免疫算法進行模型求解,但僅簡單采用加權法進行多優化目標的處理,加權系數選取困難。文獻 [9]采用遺傳算法解決了以網損最小、電網改造升級投資最少和發電機耗費最省為目標的分布式電源接入優化問題。文獻 [10]研究了考慮供電可靠性的分布式電源選址與定容問題,隨機生成故障集,以減小配網故障后的平均停電量為優化目標,但缺乏對分布式電源接入經濟性因素的考慮。文獻 [11-12]在分布式電源接入優化問題的研究中,考慮了經濟性因素,例如網絡有功損耗、節點平均電壓偏移等。可以看到,目前分布式電源選址定容方案的研究較少同時考慮經濟性和可靠性因素,少數研究建立的多目標優化模型存在多目標處理簡單的問題,加權系數選取與實際情況相差較大,導致優化結果難以實際應用。

本文對同時考慮供電可靠性和運行經濟性的分布式電源選址定容方法進行了研究,給出了以配電網網損和分布式電源總費用為代表的經濟性指標計算方法。基于含分布式電源配電網孤島的劃分,采用對偶抽樣序貫蒙特卡洛模擬法進行以系統平均停電持續時間和系統平均電量不足為代表的配電網可靠性指標計算。建立了多目標分布式電源選址定容優化模型,采用粒子群優化與非支配遺傳排序協同進化算法進行模型求解,給出了在IEEE33節點標準系統中應用的算例。

1 分布式電源選址定容指標計算

1.1 經濟性指標

綜合考慮配電網和分布式電源雙方的經濟性,分別選取有功網損和分布式電源總費用為經濟性指標。

1)配電網網損

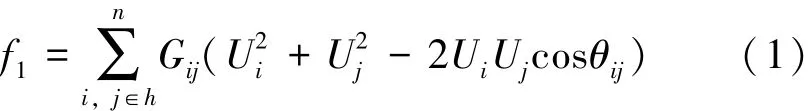
式中,f1為配電網總有功損耗；i和j分別為網絡支路兩端節點號；Ui和Uj分別為節點i和j的電壓幅值；Gij和θij分別為節點i和j之間的電導和電壓相角差；h為配電網支路集合；n為配電網支路總數。配電網網損通常采用前推回代法計算得到[9]。

2)DG總費用

DG總費用包括DG投資成本和運行成本。

DG投資成本f2計算公式為:

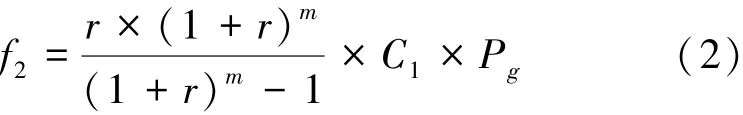
式中,f2為DG投資成本；r為貼現率；m為DG使用年限；C1為分布式電源單位投資成本；Pg為分布式電源額定容量。

DG運行成本f3計算公式為:

式中,f3為DG運行成本；C2為分布式電源單位容量運行成本。

1.2 可靠性指標

配電網系統可靠性評估即基于元件的可靠性參數來計算其可靠性指標,具體步驟可分為元件可靠性建模、系統狀態選擇、系統狀態分析和可靠性指標計算。其中系統狀態選擇算法主要分為解析法和模擬法兩大類。評估含有分布式電源的配電網的可靠性時,應考慮到分布式電源的特殊性,在現有評估方法的基礎上加以改進。

傳統配電網中一旦某元件發生故障,則其上游開關將立即斷開以隔離故障,造成開關下游負荷需待故障修復后才可恢復正常供電。分布式電源的接入使配電網出現了一種特有的運行式—— “孤島運行”。孤島中的負荷在一定條件下仍可正常運行。因此,進行孤島劃分是含分布式電源配電網可靠性評估的首要工作,采用如下步驟。

步驟①:形成分布式電源結構圖。即配電網末端開始,向饋線上游尋找分布式電源,將其劃分為一個停電區域,相鄰分布式電源間饋線劃分為一個停電區域,直至遍歷完配網所有DG；

步驟②:對第i個形成的區域Si,令區域容量APi等于DG發電量Psi；

步驟③:基于配電網結構圖搜索區域外的負荷,按負荷容量由高到低的順序依次考察,只要找到某個相鄰的負荷區域Lj,滿足APi≥PLi,則將此負荷區域融入區域Si中,并轉至步驟④,否則轉至步驟⑤；

步驟④:令APi＝APi-PLj,轉第步驟③；

步驟⑤:得到第i個DG的一個供電區域,其范圍從該DG延伸至負荷j前一個負荷；

步驟⑥:若仍有DG未計入,則得到第i個孤島的運行邊界,令i＝i+1,轉至第步驟②；

步驟⑦:遍歷完所有DG和負荷,得到孤島劃分方案。

確立孤島劃分方案后,采用可有效降低抽樣次數,提高抽樣效率的對偶抽樣序貫蒙特卡洛模擬法計算配電網可靠性指標[13]。計算流程如圖1所示。

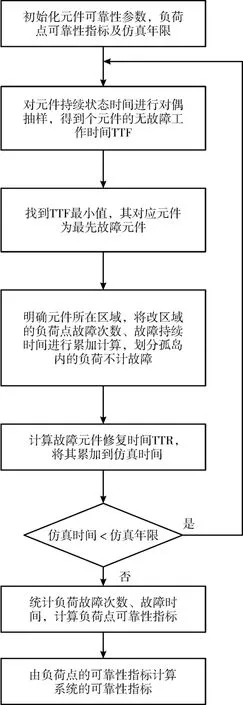
圖1 配電網系統可靠性指標計算流程

選取系統平均停電持續時間指標 (SAIDI,h/(戶·年))和系統平均電量不足指標 (AENS,MWh/年)衡量配電網供電可靠性,并分別作為優化求解的經濟性指標之一,即:

式中,Ui為負荷點i的年平均停電時間；Ni為負荷點i的用戶數；Lai為接入負荷點i的平均負荷。

此外,還考慮靜態電壓穩定裕度,并將節點電壓偏差作為優化目標函數之一,即:

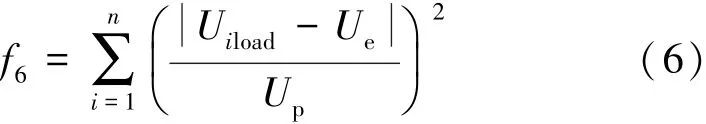
式中,Uiload為負荷點i的節點電壓標幺值；Ue為負荷節點額定電壓,取為1；Up為節點電壓允許偏差,取為5%。

2 計及供電可靠性的DG選址定容優化模型

2.1 目標函數

計及供電可靠性的多目標DG選址定容方法,考慮分布式電源接入對配電網供電可靠性的影響,在滿足各約束條件的前提下最大化配電網和分布式電源效益,并使得配電網可靠性最優,節點電壓偏差最小。優化模型的目標函數為:

式中,子目標函數f1、f2、f3衡量選址定容方案的經濟性,分別為配電網網損、DG投資成本、DG運行成本；子目標函數f4和f5衡量選址定容方案對配電網可靠性的影響,分別為DG接入后的系統平均停電持續時間和系統平均電量不足；子目標函數f6考慮節點電壓偏差。

2.2 約束條件

1)潮流等式約束

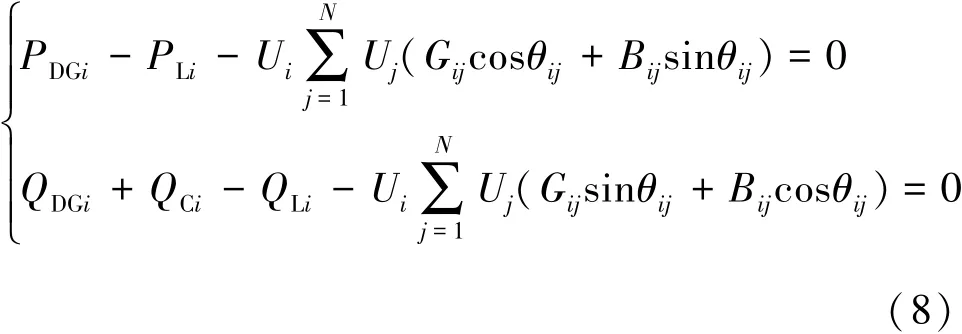
式中,N為配網總節點數；Gij和Bij分別為節點i和j間饋線電導和電納；PDGi和QDGi分別為節點i分布式電源注入的有功和無功功率；PLi和QLi分別為節點i負荷的有功和無功功率；QCi為節點i處無功補償容量。

2)節點電壓約束

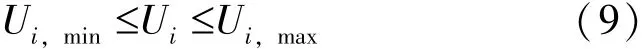
式中,Ui,max和Ui,max分別為節點i電壓的上下限。

3)DG注入功率約束

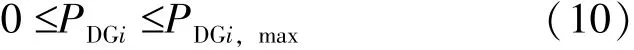
式中,PDGi,max為節點i分布式電源注入有功功率的上限。

3 選址定容優化模型的求解

粒子群優化 (PSO)算法在求解大規模優化問題上具有很快的收斂速度和全局尋優能力[6],但實際上是一種單目標優化求解方法,在求解多目標優化問題時,一般是將各子目標函數賦予權重系數,轉化成單目標問題求解。但每個子目標具有不同的物理意義和量綱[14],權重系數的選擇一般依據經驗主觀決定,可能與實際情況偏差較大。非支配排序遺傳算法 (NSGA)適用于求解多目標優化問題,但算法計算復雜度較高,用時較長。本文提出粒子群優化—非支配遺傳排序協同進化算法(CPSO-NSGA)來求解分布式電源選址定容的多目標優化問題,如圖2所示。

圖2 CPSO-NSGA算法流程

步驟①:初始化。包括在約束條件范圍內隨機產生粒子群的初始位置及速度、粒子種群大小、設定最大迭代次數以及目標函數個數等；

步驟②:據粒子初始位置,即初始各負荷節點的分布式電源接入容量,調用潮流程序計算網絡損耗,再調用蒙特卡洛模擬程序計算可靠性；

步驟③:基于小生境技術對初始種群進行多目標全局尋優；

步驟④:對粒子速度函數進行更新,再更新粒子位置,判斷粒子的速度和位置變量是否越限,對其進行約束；

步驟⑤:求得更新后各粒子的子目標函數值,形成混合種群,進行非支配排序,選擇下一代種群；

步驟⑥:計算得到當前全局最優解,檢查是否達到最大迭代次數,如果沒有達到最大迭代次數則轉步驟③,否則轉步驟⑦。

步驟⑦:輸出最優解,程序結束。

其中,基于小生境技術的多目標全局尋優過程為,首先初始化各方案適應度值,將其設置為0；生成區間范圍為 [1,2]的隨機數k,針對每一個優化目標,對方案進行排序,計某方案排序為i,若i＝1,即為該子目標下的最優方案,則適應度值累加k·pop,pop為方案數,否則累加 (pop-i)2。最優解為各子目標適應度值累計最小的方案。

4 算例分析

算例采用IEEE33節點標準測試系統,該系統有32條支路、5條聯絡開關支路、1個電源網絡首端基準電壓12.66 kV、三相功率準值取10 MVA、網絡總負荷5 084.26+i2 547.32 kVA。設定單節點安裝DG容量不高于100 kVA。網絡拓撲如圖3所示,各支路數據及負荷情況見表1,可靠性數據見表 2—5。

圖3 IEEE33節點配電系統接線

表1 IEEE33節點配電網數據

續表1

表2 配電網參數表

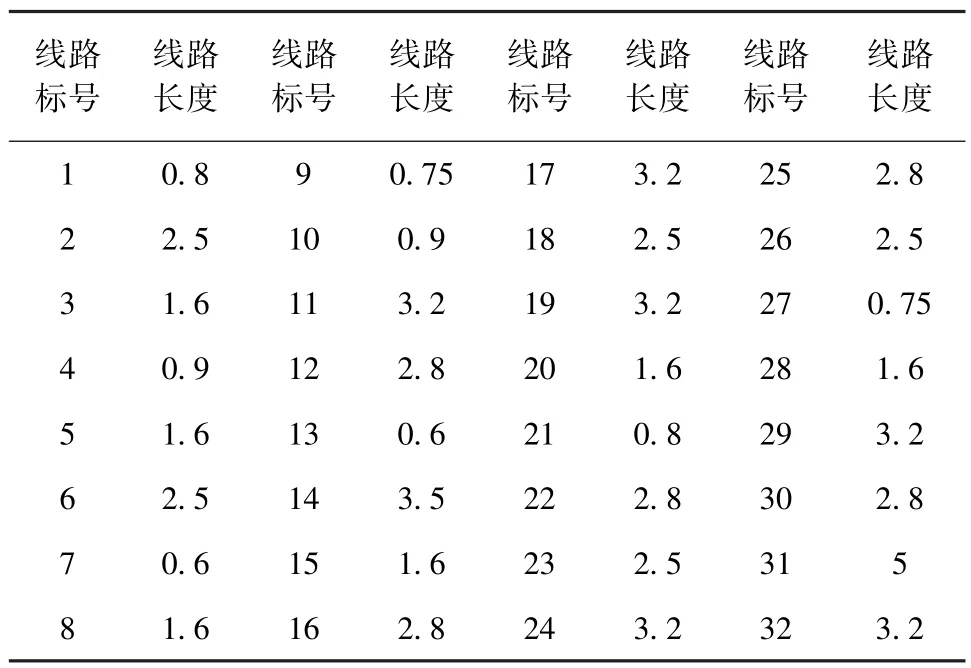
表3 線路長度參數表 km

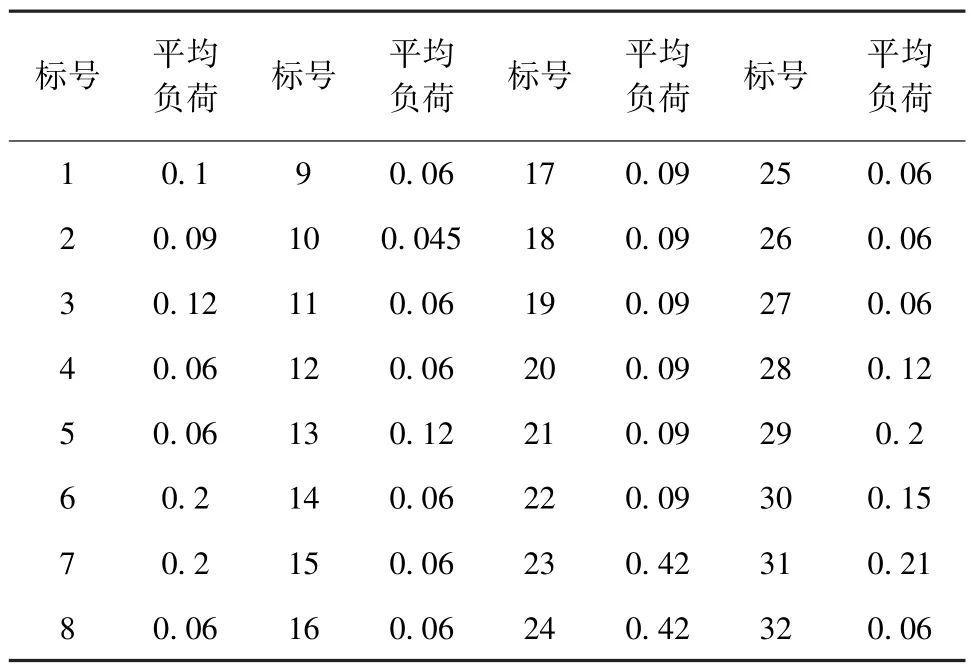
表4 負荷點平均負荷參數表 MW

表5 負荷點用戶數參數表

采用CPSO-NSGA算法求解計及供電可靠性的多目標DG選址定容優化模型。初始參數為:初始種群大小為90,即每代種群中含有90個粒子；最大迭代次數200；子目標函數個數最大值為6,即最多可同時優化6個子目標；控制變量2個,即允許接入分布式電源的數量為2,且各節點分布式電源接入容量為0～500 kVA,功率因數均取0.9,此外考慮到對所有節點進行選址情況過于復雜,且為了更加負荷實際情況,在供選節點8,9,11和節點29,30,31中加裝DG。

圖4為200次迭代后的最優種群中,配電網網損隨DG接入方案的變化；圖5為分布式電源總投資和運行成本變化；圖6為電壓總偏差變化；圖7和圖8分別為系統平均停電時間和系統平均電量不足變化。對于可靠性計算部分仿真而言,形成的兩個孤島共包含8個節點,分別是4,5,8,9,10,16,25,26號節點。

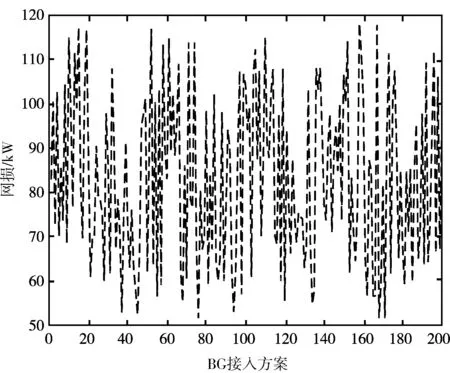
圖4 網損變化

圖5 DG總投資和運行成本

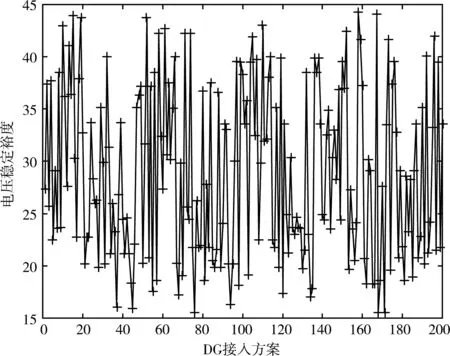
圖6 靜態電壓穩定裕度

圖7 配電網平均停電時間

圖8 配電網平均電量不足

由圖4—8可以看出,就某DG接入方案而言,無法使得各子目標均達到最優。例如,當選取網損最小即方案172時,此時網損為53.6 kW,而DG總投資和運行成本為15.3萬元,靜態電壓穩定裕度為34.6,配電網平均停電時間為854.32 h,配電網平均電量不足為2.37 MW,可以看到靜態電壓穩定裕度指標嚴重偏大,采用該方案易出現電壓越限的情況,而且該方案停電時間也較長,對電網用戶影響較大。

表6給出了選址定容最終的優化方案,即節點1接入分布式電源459.42 kVA,節點11接入303.28 kVA,該最優方案是基于小生境技術在最優種群中選出一個適應度較大的個體作為最優解,可保證各子目標函數非劣程度最好。表7為采用表6方案時的各子目標函數值及算法性能。由表7可以看出,該方案各子目標函數值均較好,沒有在某個子目標維度上出現極端劣解,在可靠性經濟性兩方面達到了綜合最優。整個求解過程耗時1 176.78 s。

表6 最優選址定容方案

表7 優化結果及算法性能

將所得到的結果與只考慮可靠性的配電網選址定容結果[10]進行對比,表8給出了兩種方案的具體接入情況及對應的各項指標,圖9為按照兩種方案接入分布式電源后的節點電壓變化,方案1計及供電可靠性的多目標,方案2只計及可靠性的選址定容。由表8和圖9可以看出,方案1在降網損以及供電可靠性方面均不如方案2,然而在DG投資成本和運行成本指標上,發出每單位功率 (MW)方案2的成本為方案1的兩倍左右,因此在不對電網用戶造成明顯影響的前提下,犧牲一部分可靠性指標換取經濟性指標對電網來說更加合理實際。

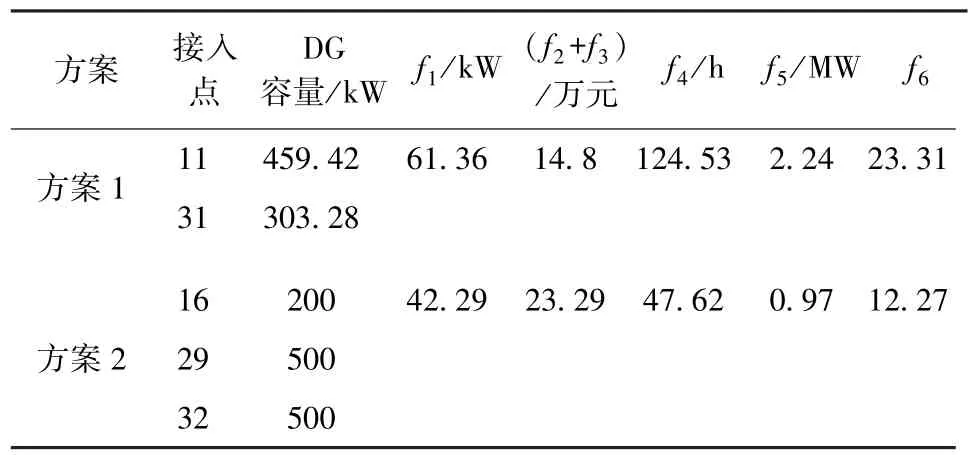
表8 DG優化結果對比

圖9 配電網節點電壓

最后,基于CPSO-NSGA求解方法和NSGA求解方法的對比,結果表明采用NSGA方法也可得到相同的優化結果,但求解時間達到1 722.5 s,超過前者46.4%,表明優化算法可有效提高多目標優化模型的求解效率。

5 結語

本文提出一種計及供電可靠性的多目標分布式電源選址定容方法,綜合考慮了對配電網供電可靠性和運行經濟性兩方面因素進行分布式接入的選址定容。采用粒子群優化與非支配遺傳排序協同進化算法 (CPS-NSGA)進行優化模型求解。將其應用到IEEE33節點系統中,并與采用PSO算法僅優化供電可靠性的算例進行對比,結果表明通過采用小生境技術在最優種群中選出相對最優解,使得DG選址定容方案在可靠性和經濟性兩個維度上達到了綜合最優,為提高分布式電源選址定容方案制定的科學性提供參考。