基于頻域和時域的索網幕墻結構風振響應

陳子立

（四川電力設計咨詢有限責任公司，四川成都 610041）

本文分別采用頻域和時域方法，分析了索網幕墻結構的風振位移響應，研究了玻璃自重導致豎索張力不均勻對風振響應的影響。使用線性濾波法模擬有效的風速時程，通過時域方法得到結構風振位移響應，并進行了在靜風平衡位置的頻域風振分析。算例表明，考慮玻璃自重時頻域方法能得到比忽略玻璃自重時更接近時域方法的風振位移響應結果，且隨著玻璃自重的增大，共振響應相差較大，位移風振系數的差別主要是其共振分量部分導致的。

0 引言

本文把平均風荷載當作靜態荷載處理，同時通過采用線性濾波法模擬出脈動風速時程，進而由風速和風壓的準定常假定得到脈動風荷載時程，兩部分合起來得到空間風荷載時程。從而對結構的風振位移響應進行時域分析。對單層平面索網玻璃幕墻結構在考慮了玻璃自重對豎索拉力產生影響的情況下，通過頻域方法對結構的風振位移響應進行計算，分析結構風振響應的背景分量和共振分量。

1 基于頻域和時域的風振響應

幕墻結構承擔的主要荷載為其所掛玻璃等的自重和風壓，對于風壓，其對幕墻結構來說為橫向荷載，必然產生彎矩和剪力，因此，幕墻結構在受荷過程中產生較大位移通過形狀的改變將彎矩和剪力轉換為軸力和面內應力。

1.1 頻域分析方法

由于這類結構的質量和剛度分布可以隨高度和寬度發生變化，其在豎向和水平向上并不均勻對稱，所以可以將結構抽象為二維的平面體系，通過隨機振動的振型分解方法分析得出任意點處的水平動位移yd（x，z，t）可以表示成：

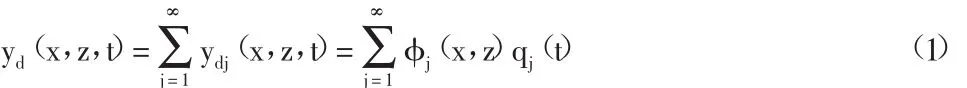
式中：ydj（x，z，t）-第j振型的動位移；φj（x，z）-第j振型（x，z）點處的坐標；qj（t）-第j振型的廣義坐標。

按照振型分解隨機振動理論，結構水平動位移響應的功率譜密度Sy（x，z，n）為：

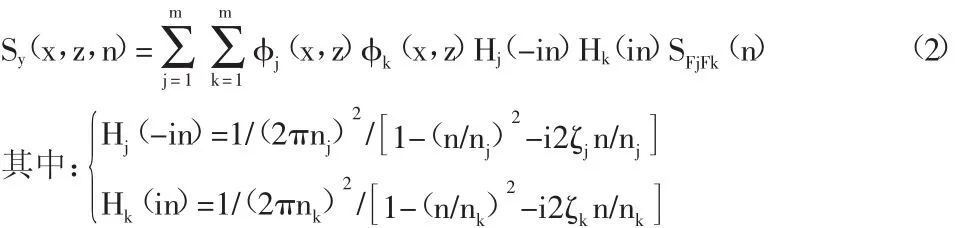
忽略交叉項后，第j振型結構動位移響應的方差可以分為三段積分的形式，為：

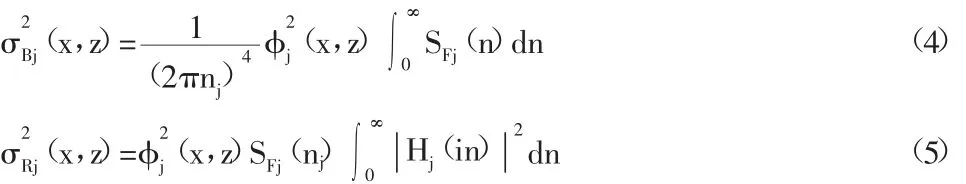
由于在風振位移響應功率譜中，背景響應部分為寬帶部分，而共振響應部分卻為非常尖銳的窄帶部分，為了保證結果的準確性，采用背景響應和共振響應組合的方法，可以表示為：

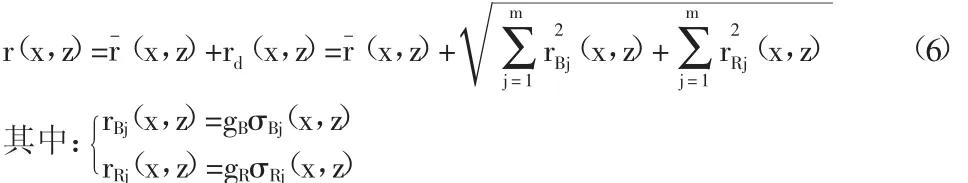
則可以得到順風向水平風荷載作用下，結構的風振位移響應風振系數為：

1.2 時域分析方法

分析計算時常常根據其特點做一些基本假設：首先，索在軸向上只承受拉力而不承受壓力；其次，索沒有抗彎剛度和抗扭剛度；最后，在應力達到屈服狀態前，索為線性材料。在此幾何非線性動力問題中，使用Newmark法。

1.3 幕墻結構的算例驗證

以某大廈單層平面索網幕墻為基礎，豎向為60m，水平向為30m的單層平面索網，以左下角為坐標原點，向上和向右為正方向，對此結構上除上下兩端支座和左右兩端支座的1711個節點處的脈動風速進行模擬，并取水平15m且豎向30m處（1631節點）的節點分析，結果滿足均值為零，且其功率譜與達文波特譜的擬合程度較好。

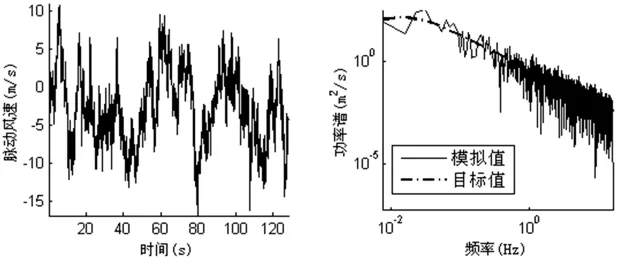
圖1 索網幕墻節點1631處脈動風速曲線和功率譜

按豎索初始預拉力為75kN，橫索初始預拉力為250kN，索密度為7850kg/m3，直徑為 0.02m，彈性模量為 1.04×1011Pa，每 1m2網格的節點掛著1m2的玻璃板，單位面積玻璃自重為500N/m2，10m高度處風速為22m/s，取2/3高度處的平均風荷載均布作用。對結構的風振位移響應進行計算。

表1 索網幕墻位移響應的方差

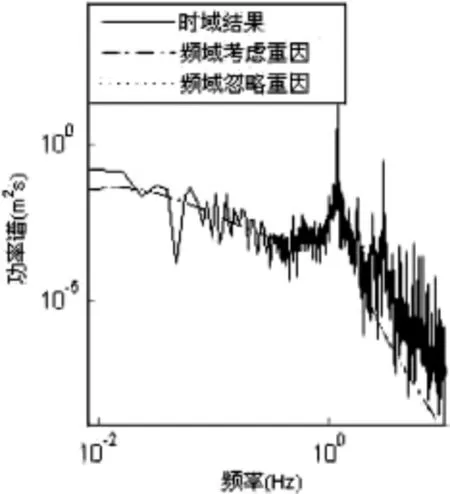
圖2 位移響應功率譜

表2 索網幕墻風振系數的變化

2 結論

本文使用頻域法和時域法分析索網幕墻結構玻璃幕墻得到的中部豎向各點的風振位移響應方差結果一致，頻域結果略大于時域結果，中部位置點的頻域法得到的位移功率譜與時域法得到的位移功率譜基本擬合，說明采用平均風壓作用位置作為結構的初始位置時，頻域分析方法能夠較為準確地計算結構的風振位移響應，且頻域分析中考慮了自重對豎索張力的影響后的結果比忽略這種影響的結果更加接近時域分析的結果。

索網幕墻結構玻璃幕墻頻域分析得到的風振系數略大于時域分析得到的風振系數，且考慮了玻璃自重對豎索張力影響的結果比忽略這種影響的結果略小，更加接近于時域分析得到的結果，這種差異主要來自于共振分量引起的風振系數不同。隨著玻璃自重的增加，結構的風振系數都大致呈增大的趨勢，對于考慮自重影響豎索張力的頻域分析、忽略自重影響豎索張力的頻域分析及其時域分析這三種分析結果保持了其相對大小關系的一致性。

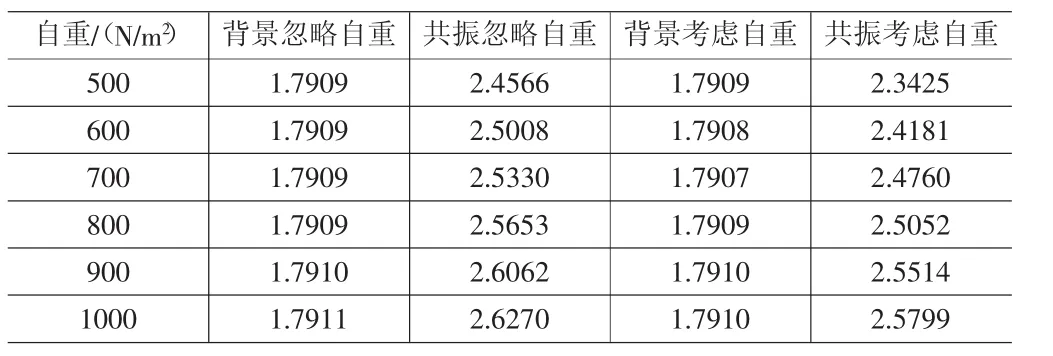
表3 索網幕墻背景分量和共振分量風振系數的變化

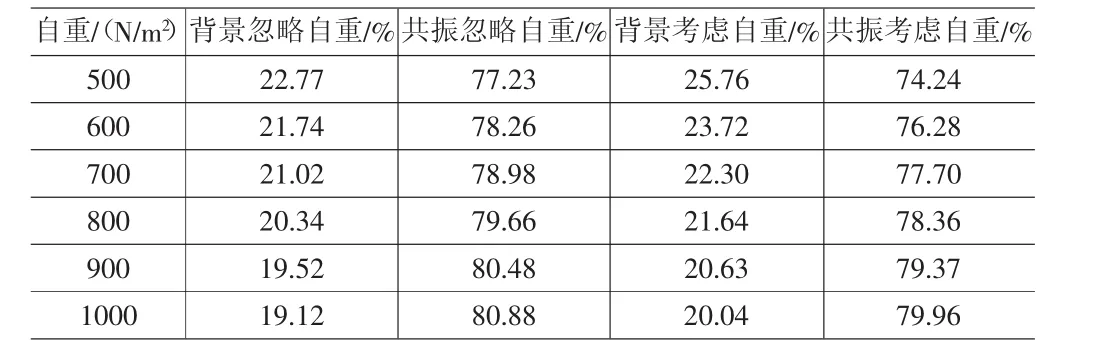
表4 索網幕墻背景分量和共振分量風振系數比重的變化

索網幕墻結構幕墻風振位移響應的背景分量引起的風振系數均小于其共振分量引起的風振系數，位移響應中的共振分量相較于背景分量均占有較大的比重，隨著玻璃自重的增大，風振位移響應的背景分量引起的風振系數均基本保持了不變，而只有其共振分量引起的風振系數有增大的趨勢，符合背景響應的準靜態特性，結合著風譜分析，共振效應增強的趨勢也和結構的柔性與風振系數隨著自重增大而增大的規律相適應。