拓撲優化在鋁合金發動機艙蓋剛度計算中的應用

龔益玲 鄭寧昆

摘要：為快速得到鋼制發動機艙蓋的鋁合金替代結構設計，引入拓撲優化設計方法進行結構模擬計算和設計。以鋼制發動機艙蓋內板結構為基礎，以保證扭轉剛度和降低質量比為優化條件，利用OptiStruct軟件進行多次迭代優化，得到相應的鋁合金艙蓋內板基礎結構，為后續的發動機艙蓋鈑金設計提供參考。

關鍵詞：拓撲優化;漸進結構優化;OptiStruct;扭轉剛度;有限元

中圖分類號：TP391.99;U463.833文獻標志碼：B

0 引言

行人保護在被動安全法規考核中的比例越來越大，基于行人保護的車輛開發越來越重要。發動機艙蓋在行人保護中起關鍵性作用，目前多使用低碳鋼材料。隨著人工智能和新能源概念的引入、新材料的發展和應用，以及車身輕量化和節能減排要求的不斷提高，鋁合金材料的汽車車身部件被各大汽車企業納入重點研究范圍。本文重點研究鋁合金發動機艙蓋的設計。由于材料特性的不同，將鋼板更換成鋁合金材料后，發動機艙蓋的結構性能會發生顯著變化。低碳鋼在發動機艙蓋設計中已大量運用，優化經驗豐富，花型和受力優化主要針對薄弱點進行局部優化。鋁合金材料的密度和彈塑性能與低碳鋼不同，因此鋁合金發動機艙蓋的受力和承力方式也將不同。原有的鋼結構替換成鋁合金材料之后無法滿足結構剛度要求，因此需要根據鋁合金自身的材料屬性設計新的發動機艙蓋內板結構。

近年來，優化算法和計算機科學迅速發展，結構優化特別是結構拓撲優化方法的研究和應用得到巨大的發展。結構優化技術被越來越多地應用于航空航天、汽車、船舶等重要工程領域中。不論是載運工具還是橋梁或某些重要的框架結構等，為達到其最佳性能，都需要進行結構優化設計。結構優化集合工程、數學和科技中的重要原理與方法，是一種非常復雜的綜合技術。

拓撲優化是在一定的空間區域（骨架結構或連續體）內尋求材料最合理分布的一種優化方法，是一個迭代尋優的過程。從定義最初的材料分布開始，每一次迭代都包含有限元分析、靈敏度計算和修改材料分布這3個步驟。在多次迭代后，材料分布趨于穩定、結構性能達到最優則優化結束。骨架結構的拓撲優化結果再加入構件特殊結構，即可直接用于設計。近年來，計算機在結構分析中普遍應用，促進結構優化數值方法的發展，將數值方法引入拓撲優化領域，使拓撲優化研究愈發活躍。目前，通用的拓撲優化軟件有德國的TOSCA、日本的OptiShape、美國的OptiStruct和Genesis等，本文采用OptiStruct作為有限元計算軟件，進行拓撲優化方法研究。

首先，從理論層面出發，簡單闡述漸進結構優化（evolutionary structural optimization，ESO）連續體結構的優化理論;然后，以數值分析為手段，以某車型的鋼制發動機艙蓋為基礎，引入鋁合金材料，針對鋁合金材料的特殊性，以拓撲優化的方法設計滿足艙蓋性能的結構;最后，對鋁合金材料的應用，尤其是在汽車開閉件輕量化設計方面的應用進行展望。本文依托某鋁合金發動機艙蓋內板的花型設計，針對實際工況中的剛度分析具體闡述拓撲優化在新材料中的應用。使用拓撲優化的方式可大大縮短發動機艙蓋設計前期力承載路徑優化的時間。在拓撲優化的基礎上結合有限元法，對花型進行二次設計和優化，可極大提高設計效率，節約開發成本。

1 拓撲優化理論基礎

ESO拓撲優化方法一經提出就在國際上引起很大的反響。ESO拓撲優化方法不僅可以解決各類結構的尺寸優化問題，還可以同時實現形狀的拓撲優化。不論是應力、位移或剛度優化，還是振動頻率、響應和臨界壓力優化等，都可以遵循ESO的統一原則和簡單步驟進行一系列的拓撲優化分析。對于靜力設計問題，ESO方法通常采用基于剛度或者應力準則的優化方法。本文以剛度準則為切入點，重點介紹ESO拓撲優化方法。

在有限元數值分析中，結構的靜態特征可以簡單描述為

Ku=P（1）

式中：K為總剛度矩陣;u為全局節點位移向量;P為節點載荷向量。

為使總剛度最大且能夠與應變能最小等價，引人平均柔度C作為結構總剛度的逆序變量，即

C=p^Tu/2（2）

考慮從某n個有限單元構成的結構中刪除第i個單元，則剛度矩陣的變化為

△K=K^*-K=K_i;（3）

式中：K^*是從結構中刪除第j個單元后新結構的總剛度矩陣;K_i是第i個單元的剛度矩陣。

假設刪除第i個單元不影響載荷向量P，忽略高階項，從式（1）可得到節點位移的變化為

△u=-K^-1△Ku （4）

由式（3）和（4）可得

△C=p^TAu/2=-p^TK^-1△Ku/2=u_i^TK_iu_i/2（5）

式中：u_i是第i個單元的位移矢量。引人一個新的定義，即

α_i=u_i^TK_iu_i/2（6）

式中：α_i為總剛度約束問題的靈敏度，該靈敏度表示由于刪除第i個單元引起的應變能變化量。事實上，α_i是單元的應變能，很容易在單元級別采用單元剛度矩陣和單元位移矢量進行計算。值得指出的是C和α_i都應為正值。

拓撲優化的目標是尋找滿足剛度約束的最輕結構，即

C《C* （7）

式中：C*是C的指定上限。當刪除一個單元時，結構總剛度減小，相應的應變能C增加。為了通過刪除單元達到優化目標，最有效的方法顯然是刪除具有最小α_i值的單元以至于C的增加量最小。因此，剛度優化問題可以簡單表述為材料刪除準則，其定義為

αjα_i，max（8）

式中：α_i，max為整個結構中最大的剛度靈敏度。

滿足式（8）的單元將被從結構中刪除。通過使用相同的只值，重復執行有限元分析、剛度靈敏度計算和單元刪除步驟，直至最后達到穩定狀態。這里，刪除率中再引入進化率E，即

R_j+1=R_j+E，j=0，1，2，… （9）

通過增加進化率，再次進行有限元數值分析和剛度靈敏度計算，然后進行相應的單元刪除，得到一個新的穩定狀態。如此循環往復，直到最后獲得滿足性能要求的最優結構。

采用OptiStruct軟件對結構相關單元進行總剛度計算，分析各個單元的靈敏度，并通過刪減相關單元達到最優化結構的目的，完成拓撲優化的過程。

2 發動機艙蓋有限元模型

基于拓撲優化的理論基礎，選取某車型鋼制發動機艙蓋作為研究對象，將該構件的扭轉剛度作為構件性能設計的基本要求。鋁合金僅用于覆蓋面積較大的發動機艙蓋內板，鉸鏈及鎖鉤的局部加強板仍舊保留鋼制材料，應根據材料不同屬性設計全新的發動機艙蓋內板結構。通過拓撲優化結合有限元模擬計算的方法，設計一款滿足性能要求的輕量化鋁合金發動機艙蓋。

2.1 鋼制發動機艙蓋模型

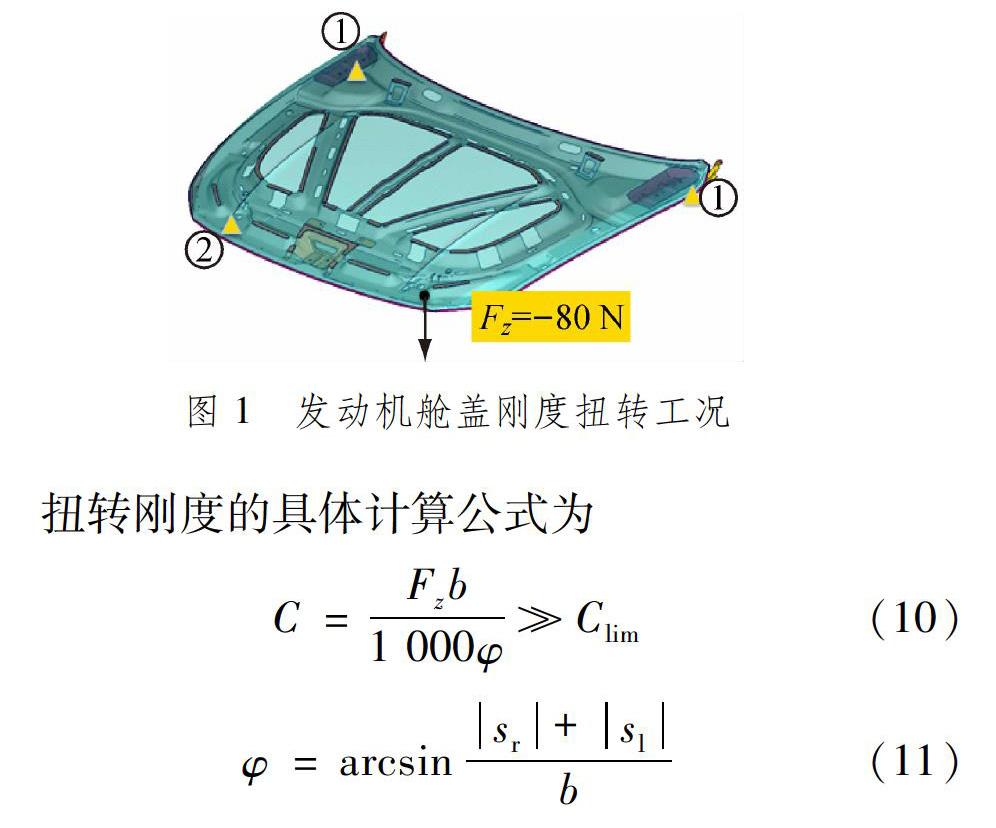
根據有限元理論和企業標準，建立鋼制發動機艙蓋的有限元模型，研究其扭轉剛度，見圖1。邊界條件及約束加載為：鉸鏈螺栓孔處約束6個自由度;右端橡膠塊位置約束z向位移D_z=0;左端橡膠塊位置施加F_z=-80N方向向下的力。

式中：b為左右兩個橡膠緩沖塊的y向間距;s_r是右側橡膠緩沖塊的z向位移;s₁是右側橡膠緩沖塊的z向位移;C_lim是該構件的扭轉剛度限值，本文定義為100.0N·m/（°）。采用Nastran有限元軟件模擬計算，可以得到該鋼制的發動機艙蓋的扭轉剛度為103.1N·m/（°），滿足構件性能要求。

2.2 初始鋁合金發動機艙蓋模型

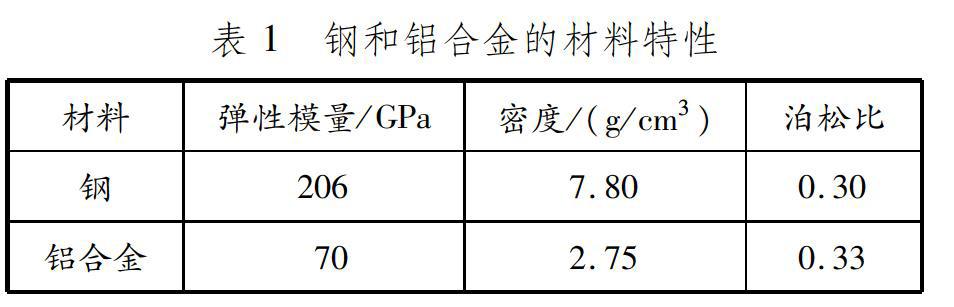
不改變原鋼制發動機艙蓋基礎結構，只是簡單地將構件改成鋁合金材料，通過調整發動機艙蓋內、外板以及內部各個加強件的厚度得到滿足性能要求的鋁合金艙蓋。鋼和鋁合金的材料特性見表1。采用Nastran軟件分析得到鋼制發動機艙蓋和鋁合金發動機艙蓋扭轉剛度的差別。有限元分析可知，鋼制發動機艙蓋的扭轉剛度為103.1N·m/（°），初始鋁合金艙蓋的扭轉剛度為80.2N·m/（°），其總質量為鋼制發動機艙蓋質量的48%。可見，鋼制發動機艙蓋改成鋁合金材料后扭轉剛度不滿足性能要求，僅通過簡單的增加厚度很難達到發動機艙蓋的性能要求。因此，需要進一步優化鋁合金發動機艙蓋，使其在滿足性能要求的前提下盡可能地實現整體結構輕量化。

2.3 初始鋁合金發動機艙蓋模型

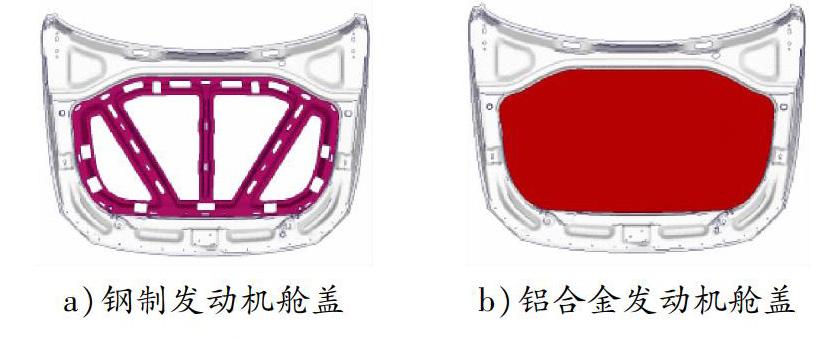
基于前文的剛度拓撲優化理論，對初始鋁合金發動機艙蓋進行拓撲優化有限元迭代計算。定義拓撲優化的區域為鋼制內板的中間區域（圖2a），同時將中間區域繪制成連續體，作為拓撲優化的基礎結構，見圖2b。在此結構基礎上，參考文獻[8-9]進行拓撲優化有限元迭代計算。

3 發動機艙蓋拓撲優化

以基礎結構為初始模型，將扭轉剛度作為約束條件，以質量最小為優化目標，采用拓撲優化有限元模擬軟件OptiStuct進行迭代計算。

3.1 初步拓撲優化結果

經過37次迭代計算，得到一個最新的優化結構，見圖3。

此內板中間區域的拓撲優化結構是在滿足扭轉剛度條件下質量最小的結構，是通過循環不斷的有限元分析、剛度靈敏度計算和單元刪除，達到結構穩定狀態得到的結果。此時，結構留下的部分均是對艙蓋扭轉剛度非常敏感的部分，在后續的構件設計中需要重點考慮。

3.2 基于構件的拓撲優化

初步優化迭代的結果一般無法應用于實際構件生產，還需要考慮鋁合金發動機艙蓋作為汽車構件的設計準則。根據初步迭代結果，可以得到鋁合金發動機艙蓋對扭轉剛度最敏感的區域，基于這些敏感區域進行更深入的內板花形結構設計。考慮零件的沖壓成型和使用功能，添加一定的翻邊和筋等結構，可得到拓撲優化構件，見圖4。

該拓撲優化構件進行有限元模擬分析，可得到鋁合金發動機艙蓋結構的剛度和質量。結果認為拓撲優化設計后的鋁合金發動機艙蓋扭轉性能是滿足設計要求的，且減重率達到40%，即在不降低結構性能的前提下可實現輕量化設計。

4 結束語

從ESO拓撲優化理論出發，利用有限元數值模擬對某車型的鋁合金發動機艙蓋進行內板鈑金結構優化。以發動機艙蓋質量最小為優化目標，以發動機艙蓋的扭轉剛度為約束條件，對發動機艙蓋內板結構進行拓撲優化，得到內板結構的基礎花型。該基礎結構的花型對結構性能靈敏度最高，以該花型為基礎進行相應的構件設計，其開發流程可以更加高效快捷。

傳統的優化方式主要針對不同加載工況中的薄弱部分進行局部強化，無法對整個受力路徑進行優化。局部強化往往會增強局部的剛度或者增大質量，難以平衡其他加載工況，拓撲優化能夠直接優化全局結構的受力路徑，防止局部剛度或者質量過度增加，使得后期所有工況調整和平衡易于進行。由此可見，在汽車鈑金設計中引入拓撲優化，不但可以大幅提升開發效率，快速開發滿足部件性能要求的結構，而且基于拓撲優化的結構可以在保證發動機艙蓋剛度的前提下考慮結構的輕量化要求。隨著汽車行業針對電動化、網聯化、智能化和共享化加大研發投入，鋁合金、塑料以及復合材料等新型材料的拓撲優化設計理念在車身開發的過程中將越來越有優勢，越來越重要。