基于GA-ELM算法的城市短期用水預測

辛珂 李文竹 劉心

摘要：準確的短期用水預測是優化供水系統的基礎，對城市水資源實時調度和城市供水系統調度有著重要意義。為了克服傳統的神經網絡預測模型訓練時間長、易于陷入局部最優的預測結果，且在少量數據樣本情況下預測精確度不足的缺點，本文提出了一種基于遺傳算法一極限學習機的城市短期用水預測方法。在引入相關影響因素的基礎上，用擅長全局搜索和并行搜索的遺傳算法對極限學習機參數進行尋優。結果表明，本模型的預測精度較高，日均絕對百分比誤差僅為2.19%，具有較強的實用價值，為未來水資源實時調度提供理論依據。

關鍵詞：遺傳算法;極限學習機;短期用水量;預測模型

中圖分類號：TV213 文獻標識碼：A

文章編號：1009-3044（2020）13-0217-04

1引言

水利是國民經濟和社會發展所必需的基本要素，為社會的發展、糧食和生態環境安全提供重要保障。隨著人口不斷向大中型城市遷移，各城市對于水資源的需求量也大幅度增加。城市供水系統的自動化運營是未來的一種發展趨勢，而用水量預測在整體城市供水系統的設計、規劃、管理和運行中起著重要的作用，是供水策略、運行調度、優化設計的關鍵性參考。因此，國內外有大量的研究試圖準確可靠的預測城市用水量，并提出了多種預測方法，如：回歸模型、人工神經網絡與差分整合移動平均回歸結合模型、時間序列、BP神經網絡模型等。早期Braun根據柏林某個居民區的歷史用水數據，提出了結合自回歸方法和考慮附加參數的回歸模型和基于季節自回歸綜合移動平均（SARIMA）模型的建模方法;楊曉俊利用時間序列分析中的移動平均模型和指數平滑模型;對柳林泉的還原泉流量進行了較為準確的預測;牟天蔚嘲提出一種基于深度學習框架的小波深度信念網絡fsw—DBN）時間序列模型，對新開河日供水量進行較為精確的預測;鞠佳偉選擇了影響因素明確、計算簡單、可隨時修正參數的多元線性回歸預測方法，建立了預測結果相對誤差較低的日供水量預測模型;郭強用貝葉斯準則優化了傳統BP神經網絡預測模型，避免了傳統BP神經網絡再預測時易陷入局部極小化和收斂速度慢的問題。

隨著智能算法理論的發展，神經網絡理論在水量預測領域得到了創新發展和應用，但傳統的智能算法如BP神經網絡存在著極易得出局部最優解以及收斂速度較慢的不足;人工神經網絡（ANN）神經網絡魯棒性不高，預測模型缺乏長效性和擴展能力等。基于此，提出通過遺傳算法（GA）優化極限學習機（ELM）的短期用水量預測模型（GA-ELM預測模型）。該方法通過GA對ELM模型的初始連接權值和隱含層神經元閾值進行優化，與其他傳統的智能算法相比，具有更快的學習速度，更好的泛化性能，并且ELM模型自身也有較強的魯棒性。最后通過北京市城區自來水水廠數據進行算例仿真并與傳統BP神經網絡預測模型及傳統ELM模型進行比較，驗證所提出的短期用水量預測結果的準確性。

2城市日用水量主要影響因素分析

2.1城市日用水量的影響因素

城市用水量通常包括生活用水、公共用水以及工業用水。而對于城市日用水量與時間、溫度、氣溫、節假日等影響因素密切相關，具有復雜性、非線性、時變性的特點，主要表現為：

（1）氣溫變化會導致城市內居民用水量變化。在溫度較高條件下，居民生活方式可能會發生改變，例如飲用水量以及清洗用水量會提升，導致生活用水量可能會呈上升趨勢。

（2）天氣的變化會影響居民的生活方式及生活行為，導致用水量發生相應的改變，同樣也會對城市綠化用水、道路灑水和水庫蓄水產生影響。

（3）節假日因素，在節假日居民在室內活動的時間會比在工作日時間長，因而居民生活用水會有增幅，同時企業用水可能會下降。若無法定假日，可將每周內的用水量視為周期性變化。

綜上，城市日用水量應存在以每日為單位的短期周期性變化以及以年為單位的長期周期性變化。因此，本文著重研究氣溫、天氣及節假日與城市日用水量之間的關系。

2.2主要影響因素篩選

3基于GA-ELM的短期用水量預測模型

極限學習機神經網絡具有預測精度高、訓練速度快的特點，但由于極限學習機模型中網絡結構的輸入層神經元與隱含層神經元之間的連接權值和隱含層神經元閾值是隨機賦值的，這會導致當給定連接權值定值為0時隱含層節點失效。而隱含層神經元的節點數量過低會降低預測結果的預測精度，過多則會出現過擬合現象。基于此本文選用尋優效果顯著的遺傳算法對極限學習機神經網絡的權值和閾值進行最優篩選，得出GA-ELM預測模型。

3.1 ELM神經網絡原理

3.2 GA改進ELM算法步驟

由3.1中敘述的模型可知，ELM算法模型的初始輸入層與隱含層的連接權值和閾值是隨機產生的，這就會造成某些時候ELM算法輸出矩陣H不是滿列秩，使得模型中某些隱含層節點無效，這樣就可能會降低ELM預測算法模型的有效性和準確性。針對這一問題，在計算輸出權重之前，對輸入權重和閾值進行基于遺傳算法的篩選，遺傳算法（GA）是一種模擬生物種群遺傳變異進化過程的一種自適應搜索技術，根據適者生存、優勝劣汰的自然法則，將所需求解的問題轉為生物種群進化的過程，過程中根據概率論方法可以自適應的改變搜索方向，以較快的速度找出最優解。通過GA對ELM進行優化，理論上可以保證輸出矩陣H的列滿秩，并且可以在一定程度上提高學習速度、預測精度、測試精度和整體網絡結構的魯棒性。

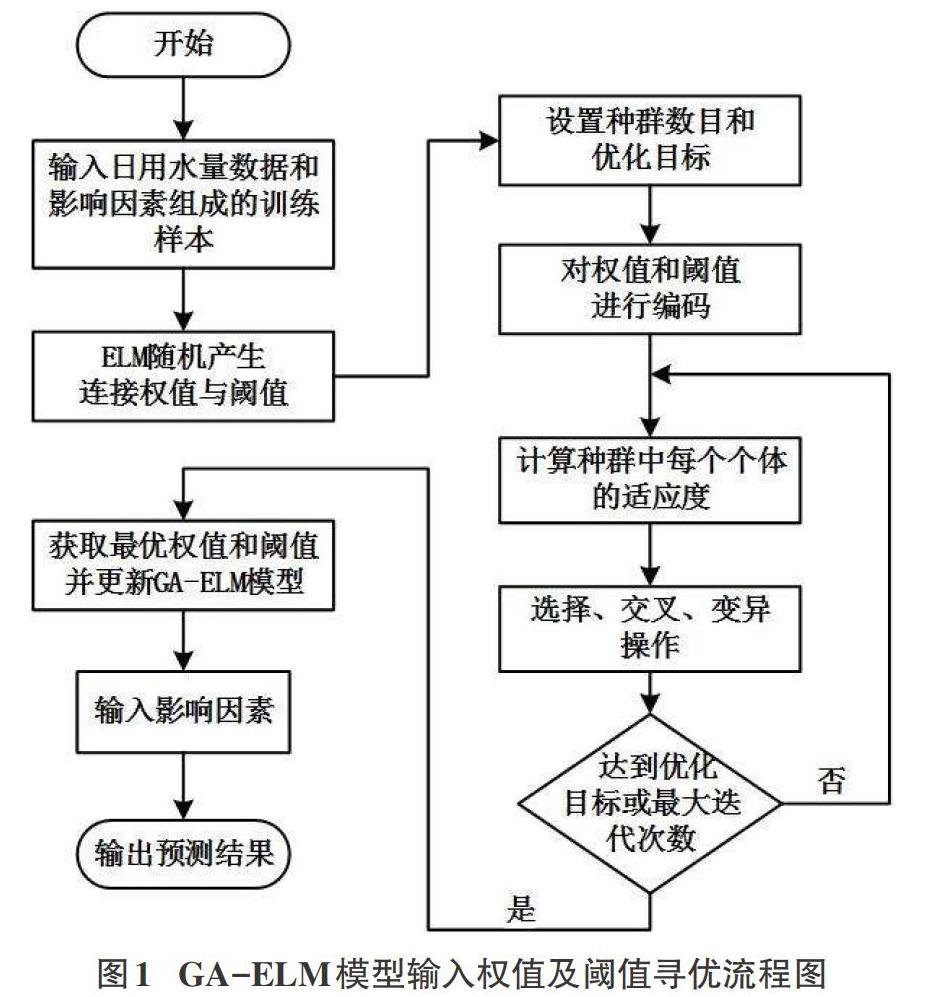
對ELM模型的權值及閾值參數尋優流程圖如圖1所示。

具體實現主要步驟如下：

步驟一：將日用水量數據和影響因素作為訓練樣本輸入。

步驟二：根據輸入的訓練數據建立隨機產生連接權值與閾值的ELM神經網絡。

步驟三：設置遺傳算法的種群數目和優化目標。優選地，選取誤差作為適應度函數，優化目標為達到目標誤差。

步驟四：對ELM模型的輸入層與隱含層的連接權值和隱含層閾值進行二進制編碼。

步驟五：對種群進行訓練，并計算種群中每個個體的適應度值。

步驟六：根據適應度值，對種群進行選擇、交叉、變異，從而產生子種群，GA的初始參數：種群大小s為60;交叉概率Pc=0.9;突變率Pm=0.01;GA的迭代次數為120;目標誤差（均方誤差/VISE）為1×10^-4。將子種群的個體插入父種群，替代父種群中適應度值最小的個體，得到新種群，同時迭代次數加1。

步驟七：判斷是否滿足結束條件。是則進行步驟八，否則返回至步驟五。結束條件設置為達到優化目標或達到最大迭代次數。

步驟八：對參數進行解碼，根據得到的最優輸入層與隱含層的連接權值和隱含層節點閾值更新GA-ELM模型。

步驟九：將影響因素輸入到預測模型，得出預測結果。

4仿真實驗

4.1樣本數據

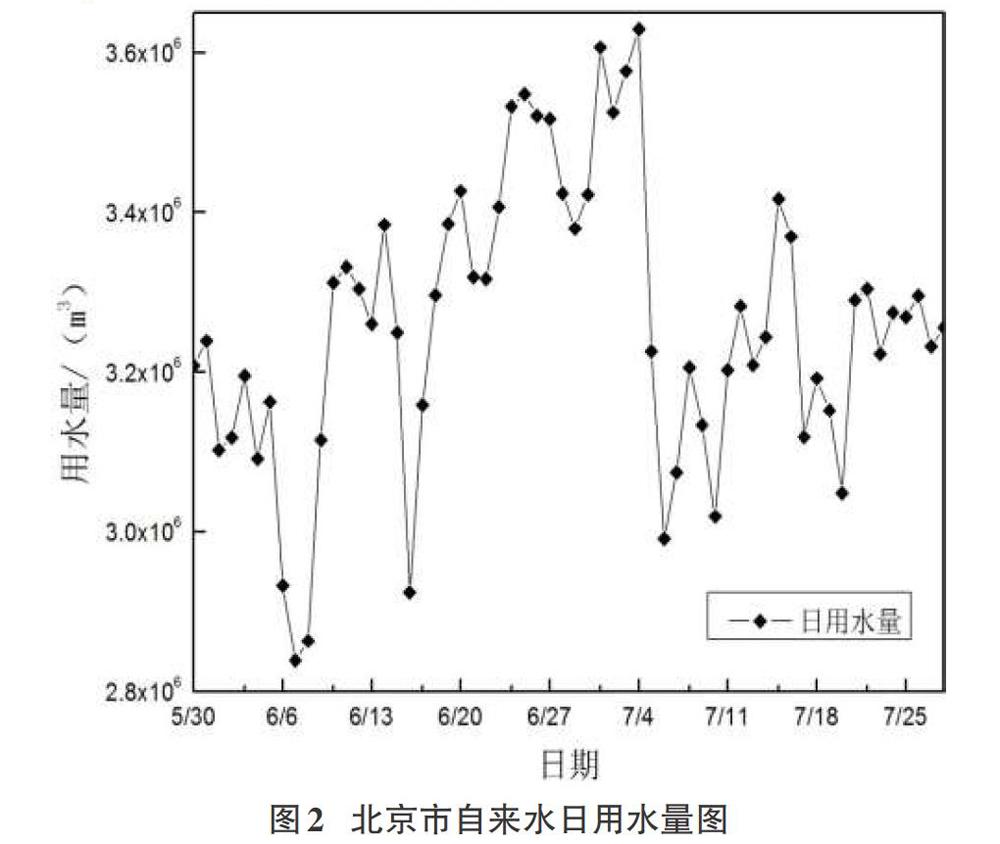
本文仿真數據為北京自來水集團市區水廠2019年日供水量數據，每日為一個樣本點，按照季節類型應該春季、夏季、秋季和冬季4種類型，僅以2019年5月30至7月28日用水量量作為樣本數據，共60天，如圖2所示，以此數據為基礎建立GA-ELM預測模型并將當日最高氣溫和最低氣溫作為模型影響因素輸入以提高預測模型的預測精度。

本文以夏季模型為例，共計60d的樣本數據。本文仿真實驗是基于北京自來水集團市區水廠歷史用水數據進行的，因此在選擇合適的輸入日用水量數據時十分謹慎，盡量使用涵蓋所有情況的數據。本次選擇的60d樣本數據沒有丟失數據和異常數據，其次，因北京市日用水量數據過于龐大而影響因素數據相對較小，在仿真實驗中要進行數據和影響因素的歸一化處理。

4.2參數設置

由于ELM網絡拓撲結構關鍵在于隱含層節點數目的確定，本文初選數目6、10、12、14、15等多種方案進行實驗比較，分析個方案下模擬結果與期望目標之間的均方誤差、絕平均對誤差及平均絕對百分誤差等指標，選取性能較好的方案，確定ELM隱含層神經元個數為12，結合輸入輸出因子數量，故網絡拓撲結構確定為2-12-1。

4.3對比模型及評價標準

為了評估本文所提出的北京市短期用水預測的模型預測結果的準確度，決定采用三種被普遍認可的評價標準，分別為可以更好地反映預測誤差的實際情況的平均絕對誤差（MAE）、直觀統計誤差的值的平均絕對百分誤差（MAPE）以及常用來作為機器學習模型預測結果衡量標準的標準誤差（RMSE）。MAE可表明預測值誤差的實際情況，MAPE可用來表示分析測試結果的精密度，RMSE則能反映一個數據集的離散程度和穩定性。

4.4結果與分析

GA-ELM預測模型與傳統BP神經網絡預測模型、傳統ELM預測模型輸出結果與性能分析結果如表2所示，輸出結果的每日絕對百分誤差結果圖如圖3所示。

從表2中可以看出，GA-ELM預測值平均誤差（MAE）相較于其他兩種預測模型最低，在龐大的百萬立方用水量數據下，平均誤差在71758.878立方米已經是很可觀的數字。由平均絕對百分誤差可以看出，在模型預測精度上也是GA-ELM精度最高，達到2.19%，傳統的ELM預測模型相對于傳統BP神經網絡預測模型優勢則并不明顯。由均方根誤差（RMSE）可以看出，GA-ELM預測模型的損失量相對于其他兩種模型最小。為了進一步說明GA-ELM模型的預測精度，圖3給出三種模型的每日絕對百分比誤差對比圖。

從圖3中可以直觀地看出，BP神經網絡預測模型最大絕對百分比誤差在7月23日為6.52%，ELM神經網絡預測模型最大絕對百分比誤差在7月26日，達到了6.36%，甚至高于同一天的BP神經網絡預測模型，而在7月28日，BP、ELM神經網絡預測模型的絕對百分比誤差達到最小，分別為2.23%和1.4%，但仍然高于GA-ELM預測模型的0.32%，整體上看，GA-ELM模型每日的絕對百分比誤差都要遠小于另外兩種對比預測模型。綜上，GA-ELM短期用水預測模型的每日預測結果穩定性、預測精度遠高于其他兩種模型。

5結語

城市日用水量具有較明顯的不確定性和隨機性，傳統的神經網絡預測方法的預測精度未能達到相對精確的預測結果，本文提出了一種基于遺傳算法一極限學習機的短期城市用水量預測模型，利用極限學習機算法訓練速度快，泛化性能強，無須調整參數的優點，并結合遺傳算法優化其輸人權值和隱含層神經元閾值的改進方法，改善了該預測模型的訓練過擬合或隱含層缺失的隱患，進而提高了模型的預測穩定性和預測精度。將該預測模型的預測結果與其他兩種預測模型的結果進行對比，結果表明GA-ELM預測模型的預測精度較高，具有較強的實用價值，從而為未來水資源調度和需水預測提供新思路。