非單調型變分不等式問題的新雙投影算法

漆林軍，何詣然

（四川師范大學數學科學學院，四川成都610066）

本文考慮經典變分不等式問題：求x*∈K，使得對所有的x∈K都滿足

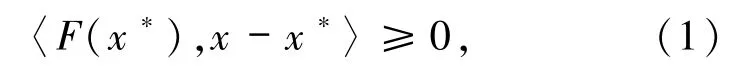
其中，F：Rn→Rn是連續映射，K是Rn的一個非空閉凸子集，〈·，·〉和‖·‖是歐氏內積和歐氏范數.記問題（1）和其解集分別為 VIP（F，K）和 S.變分不等式問題在工業、經濟、管理學等領域都有極其重要的作用，投影算法作為求解變分不等式問題的簡潔算法之一，吸引了眾多學者的研究.最早的投影算法來源于 Goldstein[1]和 Levitin 等[2]對盒子約束極小化問題的梯度投影算法，借助于巴拿赫不動點定理（參見文獻[3]中定理2.1.21），在假設變分不等式問題（1）中的映射F是強單調和Lipschitz連續的條件下，建立了算法的全局收斂性；之后，Korpelevich[4]提出了一種外梯度算法，在每次迭代過程中計算2次投影，將強單調假設條件削弱到了偽單調；再后來，Iusem等[5]引入 Armijo型線性搜索去掉了Lipschitz連續假設條件，雙投影算法的標準假設變成了映射F是連續和偽單調的，詳細發展過程與具體情況參見文獻[3，6].最近，Ye 等[7]在對偶變分不等式有解的條件下，提出了一類投影算法，該算法不假設任何的單調性條件.所謂的對偶變分不等式問題是：求x*∈K，使得對所有的x∈K都滿足

記問題（2）及其解集分別為 DVIP（F，K）和 SD.本文通過選取不同的超平面提出了新的算法.數值實驗表明新的算法依然有效；更進一步，數值實驗還表明對于一些實際問題，某些新超平面的算法比文獻[7]中的算法收斂更快.

1 預備知識

引理1.1[7]若F是連續的且K是非空凸的，則SD?S.

定義1.1設 X?Rn是一個非空閉凸集.表示向量 z到K的距離，ΠK（z）表示向量 z在 K 上的投影，即 ΠK（z）滿足

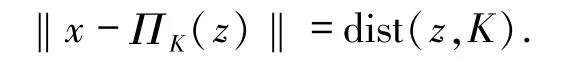
引理1.2[8]設K?Rn是一個非空閉凸集，x0∈Rn，以下不等式成立：

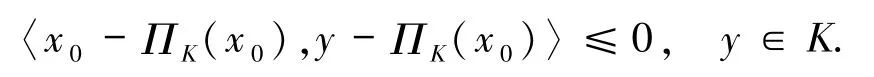
為了方便以后知識的引入，記

引理1.3[3]若μ＞0，則以下2個命題等價：

（a）x∈S；

（b）‖rμ（x）‖ =0.

引理1.4[9]若 x∈K ，μ ＞0，則以下不等式成立：

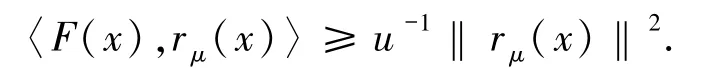
定義1.2映射 F：K?Rn→Rn，任意 x，y∈K，c＞0，若

1）〈F（y）-F（x），y-x〉≥c‖y-x‖2，則稱 F在K上是強單調的，c是F在K上的強單調系數；

2）〈F（y）-F（x），y-x〉≥0，則稱 F 在 K 上是單調的；

3）〈F（x），y-x〉≥0 蘊含〈F（y），y-x〉≥0，則稱F在K上是偽單調的；

4）‖F（y）-F（x）‖≤c‖y-x‖，則稱 F 在 K上是Lipschitz連續的，c是 F在 K上的 Lipschitz常數.

引理1.5[9]設K?Rn是一個非空閉凸集，φ是Rn上的實值函數，記

若A非空并且φ在K上θ-Lipschitz連續（θ＞0），則對任意x∈K，以下不等式成立：

2 雙投影算法

首先給出新的雙投影算法.

算法2.1

步驟1 選取初始點x0∈K和參變量.取 i=0，K-1=K.

步驟2 計算 rμ（xi）.若 rμ（xi）=0，則停止；否則，轉到下一步.

步驟3 尋找最小的非負整數mi使得

計算 ηi=γmi，yi=xi- ηirμ（xi），選取參數并轉到下一步.

步驟4 計算xi+1=ΠKi（xi），其中

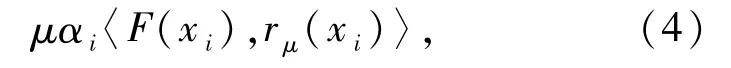
令i=i+1，回到步驟2.

在后文中，總假設以下2個條件成立：

（A1）F：Rn→Rn是連續的；

（A2）SD≠?.

下面說明算法2.1是有意義的.

性質2.1對每一個i∈N，步驟3總可以找到一個有限的非負整數mi.

證明若存在某個i0∈N使得對所有整數m都有

由假設（A1）和內積的連續性，令m→∞得到

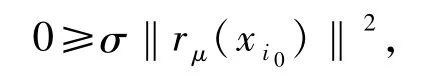
但注意到σ＞0與步驟2中rμ（xi0）≠0，這是不可能發生的.

性質2.2設hi是算法2.1中定義的函數，對所有的i∈N，都有

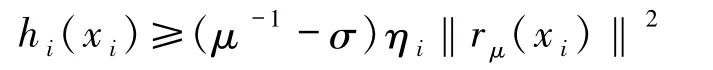
和SD∈Hi成立.

證明一方面，由ηi的定義有

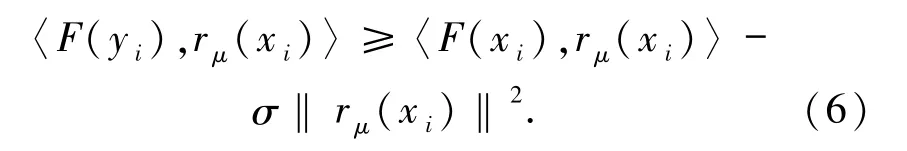
那么

另一方面，任取x*∈SD，有

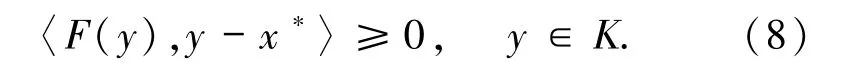
而 xi∈K，因此

再由引理1.2有

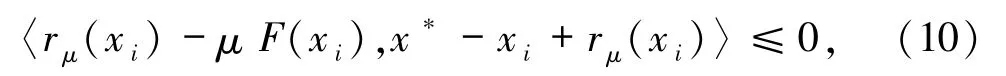
由（9）和（10）式可知

又由于

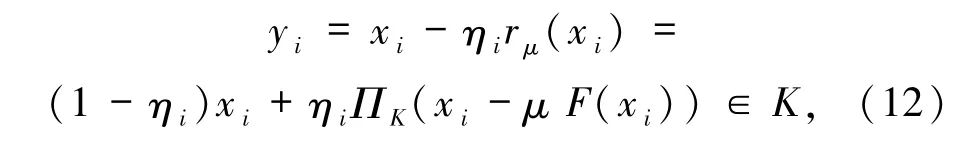
有

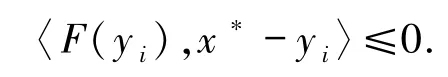
因此

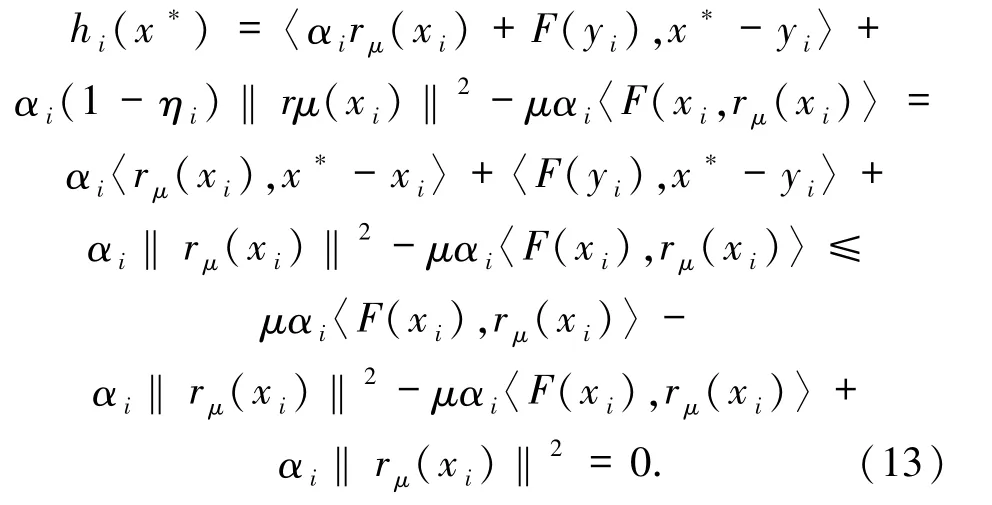
性質2.3對任意i∈N，Ki是一個非空閉凸集.更進一步，步驟4是良定的.

證明對任意i∈N，Ki是閉凸集K和有限個超平面Hj，j=0，1，…，i-1 的交集，因此也為閉凸集.又由性質2.2知對所有i∈N，SD?Ki.故當假設（A2）滿足時，對所有的i∈N，Ki也是非空的.

3 收斂性分析

若｛xi｝i∈N是由算法2.1所產生的有限序列，則存在 i0∈N，使得 rμ（xi0）=0 或 rμ（yi0）=0，由引理1.3，xi0或 yi0為變分不等式（1）的一個解，故后文均假設｛xi｝i∈N是由算法2.1所產生的無窮序列.

定理3.1若｛xi｝i∈N是由算法2.1所產生的無窮序列，則對任意，序列是一個收斂序列.

證明由于｛xi｝i∈N是由算法2.1所產生的無窮序列，則對任意 i∈N，rμ（xi）≠0.由算法 2.1 步驟 4，xi+1=ΠKi（xi）和引理1.2，對任意

有

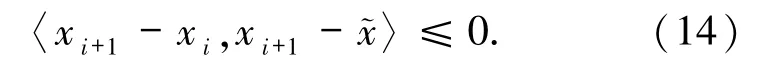
因此

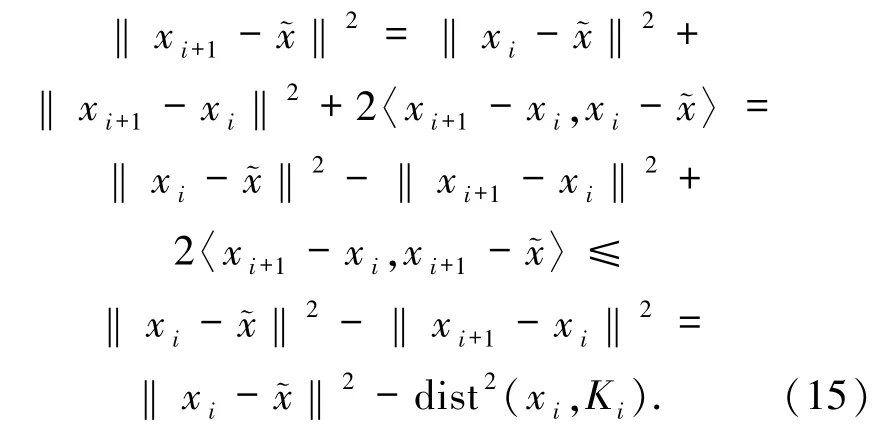
定理3.2若｛xi｝i∈N是由算法2.1所產生的無窮序列，則序列｛xi｝i∈N、｛yi｝i∈N、｛rμ（xi）｝i∈N和｛αirμ（xi）+F（yi）｝i∈N均有界.

證明由定理3.1，可知｛xi｝i∈N有界.然后由投影的連續性與假設（A1），可得｛yi｝i∈N、｛rμ（xi）｝i∈N和｛αirμ（xi）+F（yi）｝i∈N亦有界.

定理3.3若｛xi｝i∈N是由算法2.1所產生的無窮序列，則

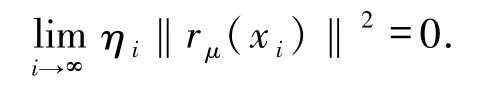
證明由定理3.2，｛αirμ（xi）+F（yi）｝i∈N有界，即存在M＞0，使得

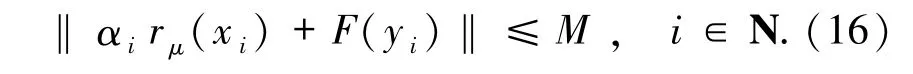
不難檢驗，hi是M-Lipschitz連續的.由引理1.5和性質2.2有

又由定理3.1有

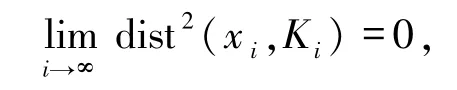
因此

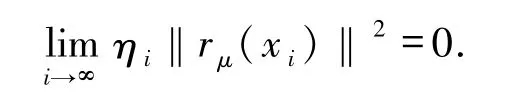
定理3.4若｛xi｝i∈N是由算法2.1所產生的無窮序列，則｛xi｝i∈N存在一個收斂到變分不等式（1）的解的子序列.

證明 由定理3.3有

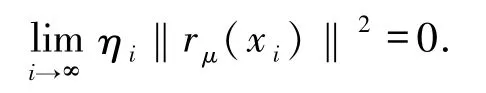
下面分2種情況討論：

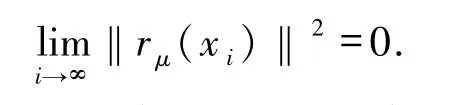
由定理3.2，｛rμ（xi）｝i∈N有界，故存在｛xi｝i∈N的某一聚點滿足

由引理1.3，｛xi｝i∈N存在一個收斂到變分不等式（1）的解的子序列.

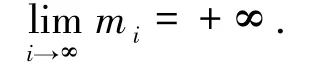
由定理3.2，｛rμ（xi）｝i∈N有界.設是｛xi｝i∈N的任一聚點，則存在｛xi｝i∈N的子序列｛xij｝ij∈N收斂到.由算法2.1和（1）式有

令 j→∞ ，有

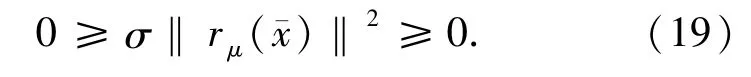
定理3.5若｛xi｝i∈N是由算法2.1所產生的無窮序列，則｛xi｝i∈N收斂到變分不等式（1）的一個解.

證明若｛xi｝i∈N是由算法2.1所產生的序列是無窮序列，則由定理3.4，｛xi｝i∈N存在一個聚點是變分不等式（1）的解.設l為任意非負整數，由算法2.1有

故對所有的i＞l，有xi∈Kl.又由Kl是閉的有∈Kl，即

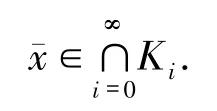
4 數值實驗

這一節用幾個數值實驗來測試不同超平面下的算法2.1，由于當α=0，μ=0時，算法2.1退化為文獻[7]中的算法，因此，不僅驗證了算法2.1的有效性，還將其與文獻[7]的算法進行了比較.使用的工具是包含7.5版本凸優化工具箱的9.1.0.441655版本的MATLAB R2016b和X550CC華碩筆記本（CPU：intel i5-3337U）.選取10-4作為停機準則，即當 ‖r（x）‖≤10-4時，程序終止.其中的參數altern代表程序循環次數；nf代表映射F的賦值次數；time代表程序的CPU運行時間，單位是s；其余的參數均來自于算法2.1.當空間維數較高時，不同超平面的算法運行下的解的維數較高，并且其分量不同，為了方便，將其省略.例4.1是一個擬單調變分不等式的推廣，n=1時是一個經典的擬單調變分不等式，在文獻[7，10]中被使用過，這里測試了n=20的情形；例4.2是一個仿射變分不等式，在文獻[9，11]中被使用過；例4.3是常用的Nash-Cournot NCP，Harker[13]給出的定義并進行了測試，文獻[9，14-15]也用其進行了測試.

例4.1設變分不等式（1）中

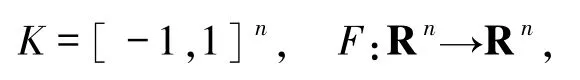
對任意的 x=（x1，x2，…，xn）∈K，

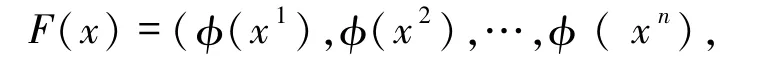
其中，

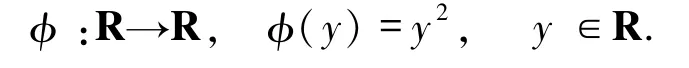
令 n=20，選取初始點x0=（0.1，0.1，…，0.1），然后在不同的超平面下對算法2.1進行測試，結果如表1.

表1 算法2.1的數值實驗結果（例4.1）Tab.1 The numerical experiment results of algorithm 2.1（Example 4.1）

例4.2當變分不等式（1）中 K=[0，1]n和F（x）=Mx+d時，其中

VI（F，K）是一個仿射單調變分不等式.選取初始點x0=（1，1，…，1）T，然后分別在 n=5 和 n=20 和不同的超平面下對算法2.1進行了測試，結果如表2和表3.

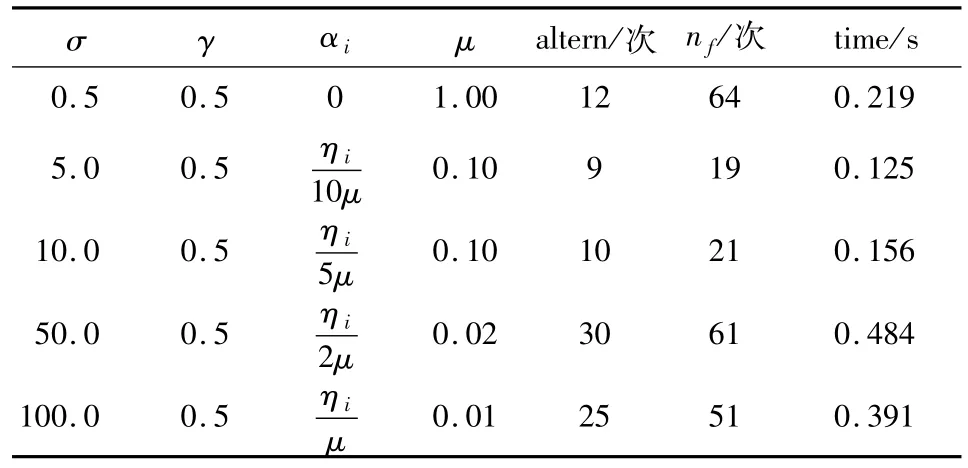
表2 算法2.1的數值實驗結果（例4.2，n=5）Tab.2 The numerical experiment results of algorithm 2.1（Example 4.2 for n=5）

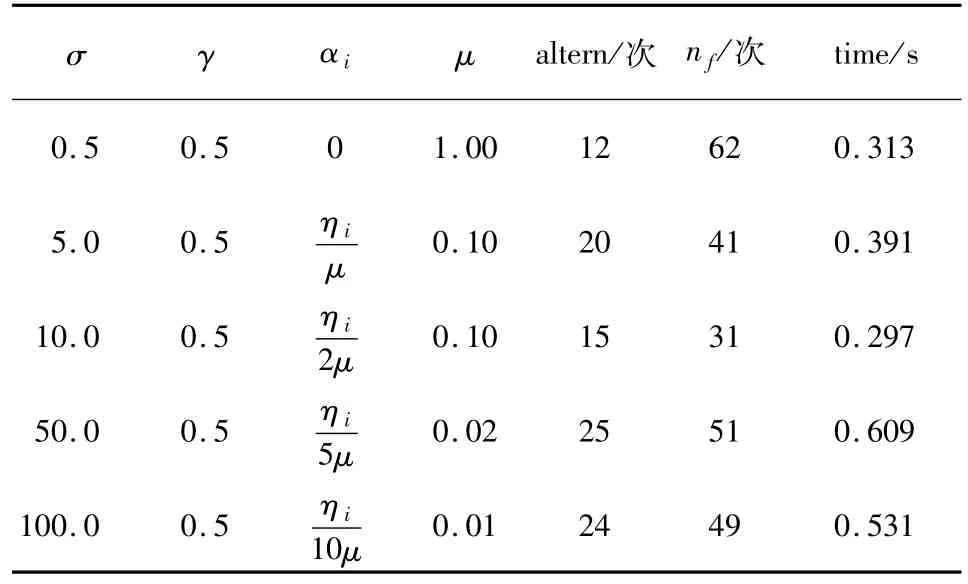
表3 算法2.1的數值實驗結果（例4.2，n=20）Tab.3 The numerical experiment results of algorithm 2.1（Example 4.2 for n=20）

例4.3PM-Nash 5 問題，來源于 Harker[13]的定義，文獻[9，14-15]也對其進行了測試.當n=5 時，選取初始點 x0=（1，1，1，1，1）T對不同超平面下的算法2.1進行了測試，結果如表4.

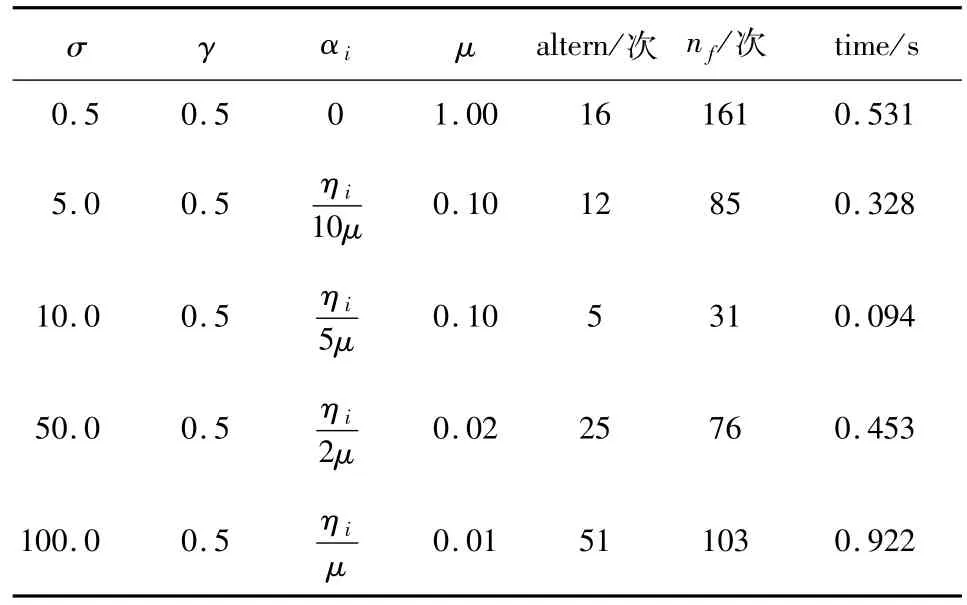
表4 算法2.1的數值實驗結果（例4.3）Tab.4 The numerical experiment results of algorithm 2.1（Example 4.3）

上面幾個數值實驗不僅表明算法2.1是有效的，還表明對于一些實際問題，某些新超平面的算法比文獻[7]中的算法收斂更快.最后，值得思考的是，借助深度學習等技術去尋找最優的超平面.