Banach格上的無(wú)界絕對(duì)弱收斂的弱Dunford-Pettis算子

伯 夏，陳滋利，陳金喜

（西南交通大學(xué)數(shù)學(xué)學(xué)院，四川成都611756）

近年來(lái)，關(guān)于Banach格及其上的算子理論的研究主要是討論算子所在的空間性質(zhì)和算子本身的性質(zhì).2014年，Gao[1]詳細(xì)闡述了無(wú)界序收斂并進(jìn)一步進(jìn)行證明；2017年，Deng等[2]詳細(xì)闡述了無(wú)界范數(shù)收斂并詳細(xì)進(jìn)行了研究；2018年，Zabeti[3]引入并討論了無(wú)界絕對(duì)弱收斂，Ozcan[4]提出了無(wú)界絕對(duì)弱Dunford-Pettis算子，記作uaw-Dunford-Pettis算子.本文基于弱 Dunford-Pettis算子和uaw-Dunford-Pettis算子的啟發(fā)，給出了uaw-w-Dunford-Pettis算子，并研究一些相關(guān)性質(zhì).

在介紹本文之前，首先給出一些基本的概念和定理.

用E和F表示Banach格，E′和F′分別表示E和F的拓?fù)涔曹椏臻g.用E+表示E中所有正元素組成的集合，記作E+=｛x∈E：x≥0｝.若 E中2個(gè)元素 x和y滿足｜x｜∧｜y｜=0，那么稱x和 y是不交的，記作x⊥y.如果滿足對(duì)E中任意的非空有上界的集合有上確界，那么E具有Dedekind完備.相似的，如果滿足對(duì)E中任意的非空有上界的可數(shù)集合有上確界，那么 E具有 δ-Dedekind完備.如果｛xα｝?E，若對(duì)?x′∈X′，有x′（xα）→x′（x），則稱xα弱收斂到 x，記作.如果｛xα｝?E，若對(duì)?μ∈E+，都有，那么就稱xα無(wú)界絕對(duì)弱收斂到零，記作.對(duì)任意 x∈E，如果x≥0，有T（x）≥0，那么稱 T是正算子；如果T=T1-T2，且T1、T2是正算子，則稱 T 是正則算子.如果

有‖T xn‖→0，那么稱T是Dunford-Pettis算子.T：E→X是一個(gè)連續(xù)算子，X是Banach空間，若對(duì)于E中的每一個(gè)范數(shù)有界不交列｛xn｝，都有‖T xn‖→0，那么就稱T是M-弱緊算子.

未解釋的有關(guān)Banach格和算子理論的一些概念、術(shù)語(yǔ)及符號(hào)詳見(jiàn)文獻(xiàn)[5-6].

1 uaw-w-Dunford-Pettis算子的相關(guān)性質(zhì)

文獻(xiàn)[4]中提出了無(wú)界絕對(duì)弱Dunford-Pettis算子，記作uaw-Dunford-Pettis算子.如果范數(shù)有界列，有‖T xn‖→0，那么稱 T是uaw-Dunford-Pettis算子.文獻(xiàn)[5]中提到一類算子——弱 Dunford-Pettis算子.如果｛xn｝?E，′，若，有，則稱T是弱Dunford-Pettis算子，并在文獻(xiàn)中對(duì)弱Dunford-Pettis算子進(jìn)行了詳細(xì)研究.結(jié)合uaw-Dunford-Pettis算子和弱Dunford-Pettis算子的定義，本文提出新算子uaw-Dunford-Pettis算子.

定義1.1設(shè)E和F為Banach格，T：E→F是一個(gè)有界線性算子.若對(duì)E中任意范數(shù)有界列xn，fn∈F′滿足，有fn（Txn）→0，則 T是uaw-w-Dunford-Pettis算子.

例子 1.2考慮 S：C[0，1]→l∞是一個(gè)正算子，定義為

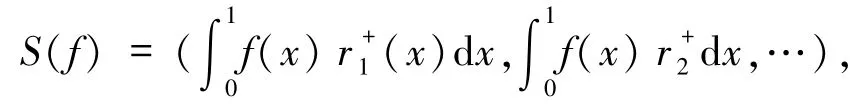
其中 f∈C[0，1]，｛rn｝是一列定義在[0，1]上的Rademacher函數(shù)列.設(shè)fn∈C[0，1]是一個(gè)范數(shù)有界的不交列且，由文獻(xiàn)[3]定理7 有.又因?yàn)?C[0，1]有 Dunford-Pettis性質(zhì)，因此，S 是一個(gè)uaw-w-Dunford-Pettis算子.

定理1.3設(shè)T：E→F是從Banach格E到Banach格F的正的有界線性算子，若E′具有序連續(xù)范數(shù)，那么下列條件等價(jià)：

1）T是一個(gè)uaw-w-Dunford-Pettis算子；

2）在E中任意的無(wú)界絕對(duì)弱零列｛xn｝和在F′中任意不交的弱零列｛fn｝，有fn（T（xn））→0.

證明1）?2） 顯然成立.

2）?1） 利用反證法證明.首先假設(shè)T不是uaw-w-Dunford-Pettis算子，那么就有無(wú)界絕對(duì)弱零列｛xn｝?E 和弱零列｛fn｝，滿足fn（T（xn））0，即?ε ＞0，對(duì)?N ＞0，?n（n＞N），使得

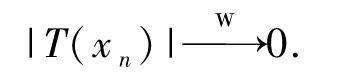
因此，令n1=1，有4 fn1（｜T（xn）｜）→0，則可以找到n2＞n1有.假設(shè)k被選定，有.因此，當(dāng)nk+1＞ nk時(shí)有

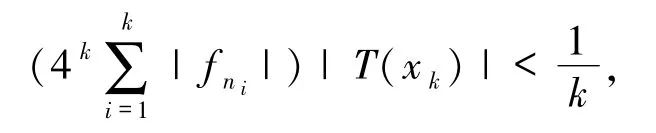
所以能找到｛xn｝的一個(gè)子列｛yn｝和｛fn｝的一個(gè)子列｛gn｝，對(duì)任意的 n≥1，滿足

和

根據(jù)文獻(xiàn)[5]中引理4.35，可以構(gòu)造如下不交列：

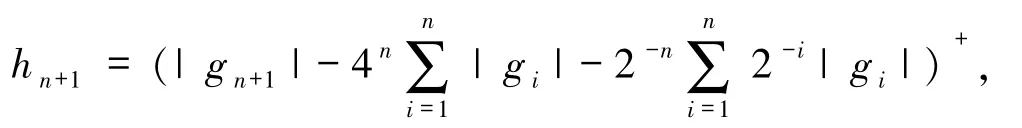
顯然有hn+1是F′中不交的弱零列，并且有

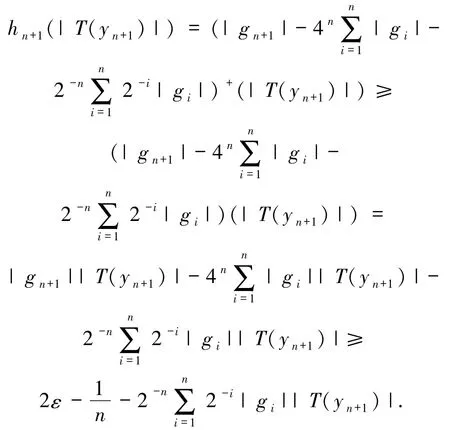
故當(dāng) n 充分大時(shí)，得到hn+1（｜T（yn+1）｜）≥ε

由文獻(xiàn)[5]定理1.23知

那么存在sn+1∈F′使得 -hn+1≤sn+1≤hn+1，且sn+1（T（yn））≥ε，由hn+1是不交的弱零列，故sn+1是不交的弱零列，這與條件（2）相矛盾.因此結(jié)論成立.

定理1.4設(shè)E、F是Banach格，T：E→F是一個(gè)正uaw-w-Dunford-Pettis算子，那么在E+中任意范數(shù)有界不交列｛xn｝和在F′中任意的弱零列｛fn｝有

證明假設(shè)｛xn｝是E+中任意的不交列，那么可以得到對(duì)?ε＞0和?f∈V，?0≤g∈F′和 k∈N，當(dāng) n＞k時(shí)，有

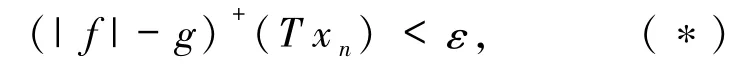
采取反證法來(lái)證明（*）.首先假設(shè)（*）是錯(cuò)誤的，那么就有?ε′＞0，對(duì)?0≤g∈F′和?N，至少?一個(gè) k（k＞ N），使得（｜fk｜-g）+（T xk）≥ε′.因此，設(shè) g=4｜f1｜和n1=1，那么就?一個(gè)n2（n2＞n1），使得

同樣地，設(shè)

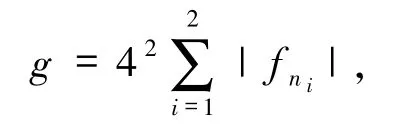
那么就?一個(gè)n3（n3＞n2），使得

通過(guò)數(shù)學(xué)歸納法，可以找到一個(gè)嚴(yán)格單調(diào)遞增的數(shù)列｛nk：k∈N｝，滿足

令

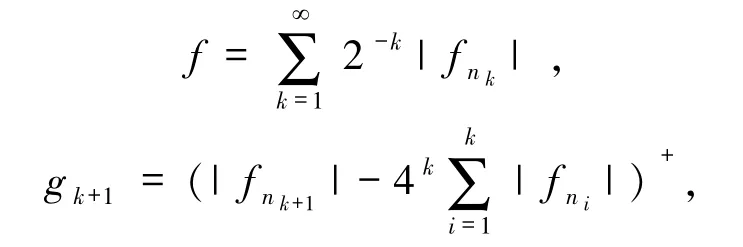
然后根據(jù)不交列的構(gòu)造技巧，設(shè)

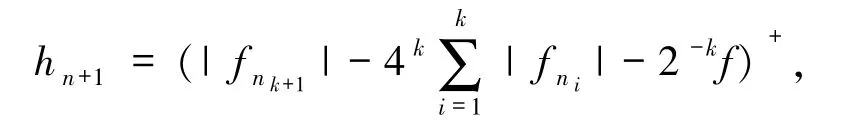
由文獻(xiàn)[5]引理4.35知，｛hn+1｝是一個(gè)不交列.由文獻(xiàn)[5]定理4.34 知，在F′中.由條件知｛xn｝是任意的不交列，那么通過(guò)文獻(xiàn)[3]引理2知，再由文獻(xiàn)[3]引理1 知.因?yàn)門(mén)是一個(gè)uaw-w-Dunford-Pettis算子，所以有hn+1（T xnk+1）→0.但是，有 0≤gk+1≤hn+2-kf，所以

因此，矛盾.所以命題（*）是正確的.

現(xiàn)在設(shè)0≤g∈F′和任意N滿足（*）.因此，當(dāng)n＞N時(shí)有

定理1.5設(shè)E、F是Banach格，T：E→F是一個(gè)正uaw-w-Dunford-Pettis算子，若F是Dedekind 完備.那么 S：E→F，其中

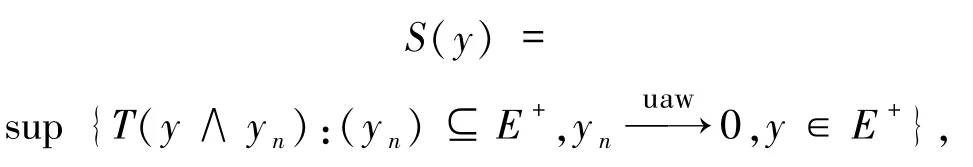
有Kantorovich延伸算子且也是一個(gè)uaw-w-Dunford-Pettis算子.

證明設(shè) x，y∈E+，，ξn∈E+，那么有

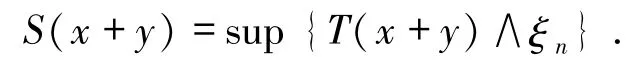
由文獻(xiàn)[6]定理6.5知

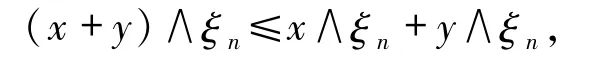
所以有

和

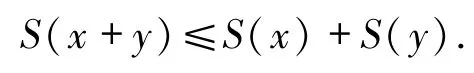
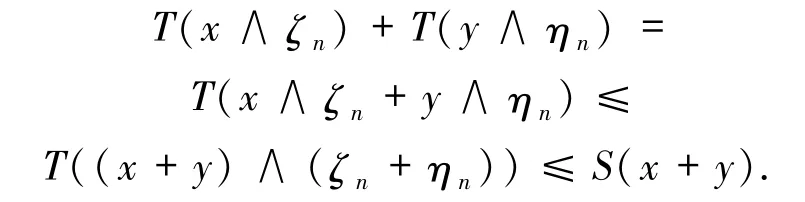
左邊取上確界，所以有

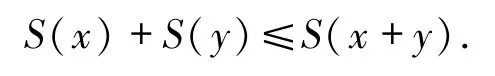
因此，S（x）+S（y）=S（x+y）.由文獻(xiàn)[5]定理1.10知，S（x）有一個(gè)唯一的Kantorovich延伸算子.接下來(lái)證明 S（x）是一個(gè) uaw-w-Dunford-Pettis算子.設(shè)

且xn，ξk∈E+，fn?F′，那么有

因此，S（x）是一個(gè) uaw-w-Dunford-Pettis算子.

2 與相關(guān)算子之間的關(guān)系

定理2.1設(shè) E、F是 Banach格，若E′有序連續(xù)范數(shù)，那么每個(gè)弱Dunford-Pettis算子T：E→F是一個(gè)uaw-w-Dunford-Pettis算子.

證明設(shè)｛xn｝是E中任意范數(shù)有界列，并且，由文獻(xiàn)[3]定理7 知，又由于T是一個(gè)弱Dunford-Pettis算子，那么有對(duì)，使得fn（T（xn））→0 成立.故結(jié)論得證.

定理2.2設(shè)T是從Banach格E到Banach格F的uaw-w-Dunford-Pettis算子，若F有序連續(xù)范數(shù)，則T是M-弱緊算子.

證明設(shè)｛xn｝為E中范數(shù)有界的不交列，由文獻(xiàn)[3]的引理2知，又因?yàn)門(mén)是uaw-w-Dunford-Pettis算子，知道｛T（xn）｝是 F 中的 Dunford-Pettis集.因?yàn)镕有序連續(xù)范數(shù)，那么就有｛T（xn）｝是緊集.另一方面，｛T（xn）｝是 F 中的弱零列，因此有｛T（xn）｝依范數(shù)收斂到零.所以，T把E中范數(shù)不交列映為范零列，故 T是 M-弱緊算子.