用Scratch把十進制轉為二進制

陳新龍

600，3/5，-7.99……這些數字都是十進制數，因為人有十根手指頭，所以最常用的是十進制。十進制就是滿十進一，滿二十進二，以此類推……十進制數字按權展開，第一位權為10^0，第二位權為10^1……以此類推，第N位按權展開10^（N-1），該數的數值等于每位的數值乘該位對應的權值之和。

在計算機的世界里除了十進制之外，常用的還有二進制、八進制、十六進制，今天我們就來講一講這個二進制。

二進制（binary）在數學和數字電路中指以2為基數的記數系統。這一系統中，通常用符號0和1來表示。數字電子電路中的高電位和低電位剛好符合二進制，因此現代的計算機和依賴計算機的設備中都用到二進制。每個數字稱為一個比特（BIT，Binary digit）。

那么日常使用的十進制數是怎樣轉換成計算機使用的二進制數呢？

我們先看一下0-10的二進制轉化十進制的對照表

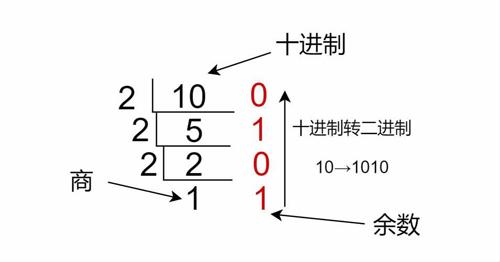
例如：十進制10=二進制1010

按權展開：

1*2^3+0*2^2+1*2^1+0*2^0=10

例如：十進制9=二進制1001

按權展開：

1*2^3+0*2^2+0*2^1+1*2^0=9

初步知道了十進制和二進制的關系后，我們思考一下如何將十進制轉化為二進制呢？大家可以去網上查閱一下。

十進制整數轉換為二進制整數：十進制整數轉換為二進制整數采用“除2取余，逆序排列”法。用2整除十進制整數，可以得到一個商和余數;再用2去除商，又會得到一個商和余數，如此重復，直到商為小于1時為止，然后把先得到的余數作為二進制數的低位有效位，后得到的余數作為二進制數的高位有效位，依次排列起來。這就是除二取余法。（圖1）

下面我們來分析將十進制正整數轉化為二進制的代碼。問題的核心是將“除2取余，逆序排列”轉化成可以執行的代碼（圖2）。

設置了四個變量，“十進制”、“二進制”、“商”、“余數”。

特別要注意二進制賦值中為空，否則最后的結果會多一位小尾巴0。

將輸入的十進制數設為“商”。對它除以2取余數，將這位“余數”存入“二進制”的個位，將“商”除以2向下取整存為下一次循環的“商”。這就是將“除2取余，逆序排列”的計算步驟轉化為編程的循環語句，一直處理到“商”=0為止。算出每次商除2的余數，將余數和二進制的數合并。這樣結果就可以出來了。

十進制小數轉換成二進制小數方法與整數不同，要用“乘2取整，順序排列”法。用2乘十進制小數，可以得到積，將積的整數部分取出，作為二進制小數的高位，再用2乘余下的小數部分，又得到一個積，再將積的整數部分取出，如此進行，直到積中的小數部分為零，或者達到所要求的精度為止。把取出的整數部分按順序排列起來，先取的整數為二進制小數的高位有效位，后取的整數作為低位有效位。

在計算機中將十進制小數轉換為二進制小數時，常常會出現無限循環的情況。由于計算機的內存空間有限，只能保留有限的小數位。這時把二進制換回十進制就會出現誤差。

比如0.3轉換為二進制是0.010011001（1001循環），0.3轉為二進制再轉回十進制就變小了。

0.3≈0.010011001≈0.298828125

這種因存儲空間導致的精度問題是編程上常見的技術問題，吃透了進制轉換對您后續的編程學習有重要的意義。