基于參數優化VMD和SPWVD的軌道波磨辨識方法

張海強，王 楠，劉 松，李柄奎

（1.廣州地鐵集團有限公司 運營事業總部，廣州 510335；2. 南京理工大學 自動化學院，南京 210094；3.中國移動江蘇公司 揚州分公司，揚州 225000）

隨著城市軌道交通技術的快速發展，地鐵運行速度逐步提升，鋼軌表面受到的沖擊愈加嚴重，導致軌道表面容易產生波磨磨耗。當車輛行駛至波磨路段時，會引起強烈的震動和沖擊，導致列車部件受損和乘客舒適度下降，嚴重時可能會發生列車脫軌事故。弦測法[1-2]和慣性基準法[3-4]是目前軌道波磨檢測的主要方法，得到了深入研究。孫銳等人[5]以實測軌道波磨數據為基礎采用ABAQUS 仿真軟件，建立了輪軌關系有限元模型，研究了不同參數對車輛駛過波磨時的動態影響，并論證了不同波磨之間存在共生關系。張厚貴等人[6]通過大量的試驗和現場調研，對波磨形成機理進行了探討，結果表明，當鋼軌模態頻率因軌下結構與輪對反共振頻率一致時，輪軌系統將發生強烈振動，引起軌面磨耗損傷，在反饋- 循環機制下，會生成與軌下模態頻率相對應的某種波長的波磨。Oyarzabal 等人[7]應用鋼軌波磨萌生和擴展（RACING）對軌道支撐結構中14 個最為明顯的因素進行優化，以實現波磨產生概率的最小化。Valehrach J 等人[8]對軌道波磨的產生環境進行分析，發現列車行駛速度是影響波磨發展的因素之一。Kurzeck 等人[9]對小半徑曲線軌道的波磨進行分析，驗證了輪軌間的摩擦振動對軌道波磨的產生具有很大的相關性，并且討論了輪軌之間的摩擦自激振動需要的條件。Zhai 等人[10]利用SIMPACK 軟件進行轉向架加速度數據仿真，利用連續小波分析得到的特征頻率和經驗模態分解得到的特征模態可以對軌道波磨進行診斷識別。黃文等人[11]研究了小波包能量熵方法，通過對波磨仿真數據的處理，能夠獲得軌道波磨位置與波長，并通過現場數據驗證了檢測方法的可行性。王乃珍等人[12]通過建立灰色區間預測模型對軌道的不平順狀態進行預測，并基于京九線的實測數據進行驗證。

本文提出了一種基于參數優化變分模態分解（VMD，Variational Mode Decomposition）和平滑偽維格納分布（SPWVD ，Smooth Pseudo Wigner-Ville Distribution）的軌道波磨辨識方法，對列車軸箱垂向振動加速度信號進行處理分析，以分解信號的包絡熵為特征量，設定故障閾值，識別軌道波磨故障，計算波磨波長并確定軌道波磨發生的位置。本方法不僅消除了VMD 分解參數選取不確定的弊端，而且克服了振動信號時頻分解過程中出現的模態混疊問題，具有良好的準確性，可輔助軌道波磨辨識，提高軌道維保效率。

1 基本理論

1.1 變步長最小均方算法

變步長最小均方（VSSLMS，VariableStep Size Least Mean Square）算法[13-14]具有計算量小、自適應能力高等優點，且其收斂速度在算法不同時期可以采用不同步長來控制，因此在信號處理的各個領域得到了廣泛的應用。

令d(n)表示期望輸出信號，W(n)表示濾波器的抽頭權向量，e(n)表示誤差信號，X(n)表示輸入信號向量，則它們有如下關系：

式中，μ(n)為步長參數，并且步長迭代關系為：

式中，μmax是獲得最大可能收斂速率的步長；μmin是具有跟蹤能力的最小步長；α＞0，β＜1，α為步長遺傳因子，主要作用是確定算法收斂時的步長值，β決定步長受誤差瞬時能量的影響程度，決定著算法的開始和跟蹤速度。

在VSSLMS 的初期階段，e(n)很大，且指數an衰減很小，因此相對的步長μ(n)比較大，算法收斂比較快。在VSSLMS 的收斂末期，e(n)較小，而指數an衰減較大，所以對應的步長μ(n)較小。由于VSSLMS 能較好地達到穩態誤差和收斂速率之間的平衡，且容易實現，因此本文用該方法對振動信號進行濾波，取得了較好的效果。

1.2 參數優化VMD

1.2.1 VMD

Dragomiretskiy 等人[15]提出了VMD 方法，屬于一類非遞歸分解方法，自適應同步提取復雜信號中的調幅-調頻分量[16]。變分模式分解將信號x(t)分解為一組本征模態分量（IMF）ck(t)，通過這些本征模態分量，可以重構信號，在頻域內迭代更新各個本征模態分量ck(t)，將本征模態分量頻譜的重心作為中心頻率ωk。

假設本征模態分量ck(t)在頻域內緊致聚集在中心頻率ωk周圍，即具有稀疏性質。每個本征模態分量的稀疏性質通過它的帶寬來描述：（1）應用Hibert變換構造其解析信號，以便獲得非負頻率的單邊頻譜；（2）通過和頻率調整至各自中心頻率處的指數諧波相乘，將頻譜平移至基帶；（3）通過梯度的平方l2范數估計帶寬。

為了將約束變分優化問題轉化為無約束形式，增加懲罰項和Lagrance 乘子，以便快速收斂并增強約束，所以，將最小化的目標函數轉換為增廣Lagrance 函數：

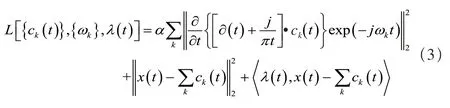
式中，λ(t)為Lagrance 乘子，α 為數據真實性約束的平衡參數表示內積。

求解與式（3）等價的最小化問題，應用最優解更新每個本征模態分量ck(t)：

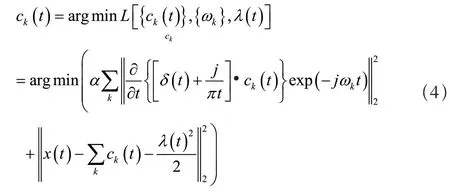
將式（4）頻域內的解取Fourier 逆變換并取實部，獲得時域里的本征模態分量。

求解和式（3）等價的最小化問題，應用最優解更新每個本征模態分量ck(t)的中心頻率ωk：

變分模式分解的完整算法如下。

（2）對于k=1，2，…，K 及所有ω(ω ≥0)，更新每個本征模態分量ck(t)及其中心頻率ωk；

（3）對于所有ω ≥0，更新Lagrance 乘子；

（4）檢查收斂條件：

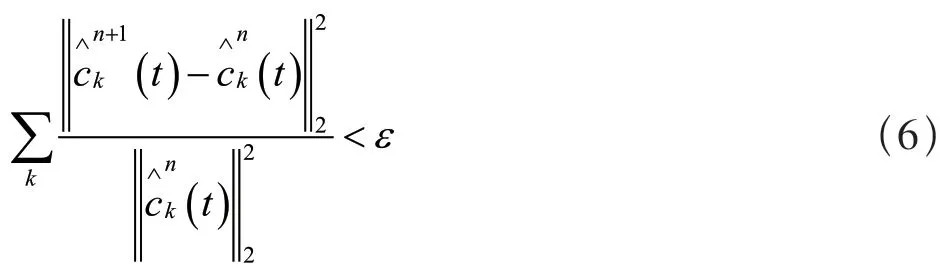
1.2.2 VMD參數優化

雖然變分模態分解具有非遞歸同步分解本質，從而有效避免了遞歸分解算法的缺點，如對噪聲的采樣敏感性，以及在極值插值過程中產生的上下包絡過擬合和欠擬合等問題，但是對振動信號分解結果影響比較大的參數分解模態數K 與懲罰參數α 卻不能自適應選取，這很容易對分解結果造成較大影響。因此，提出了一種基于變分模態分解信號中IMF 分量最大峭度值參數優化選擇方法。參數優化VMD 算法的流程如圖1 所示，詳細步驟如下：

（1）設定參數α 的搜索區間為[200 3 000]，搜索步長為10，參數K 的搜索區間設為[2 10]，搜索步長為1，在（K，α）的坐標平面上構建了一個二維網格；

（2）選取（K，α）平面網格點上的參數值，對原始信號實施變分模態分解；

（3）求出分解后的原始信號各IMF 分量中最大峭度值并保存；

（4）遍歷網格中所有的點，并完成步驟（2）、步驟（3）；

（5）從保存的峭度值中篩選出最大的，這個最大峭度值所采用的參數K 值與α 值即為最優。

圖1 參數優化VMD算法流程

1.3 SPWVD

維格納分布（WVD，Wigner-Ville-Distribution）是非平穩信號分析中常見的二次型時頻分布，廣泛應用在各種領域[17]，但WVD 可能會產生交叉項，從而輸出虛假分量。因此，為避免信號分析時的交叉項干擾，獲得良好的信號時頻分析效果，本文采用時域加窗的WVD 對信號的WVD 在時域和頻域做平滑處理的方法進行時頻分析[18]。

根據WVD 的特性，兩個時域信號乘積的WVD與各自WVD 在頻域的卷積相等，因此可以表示成：

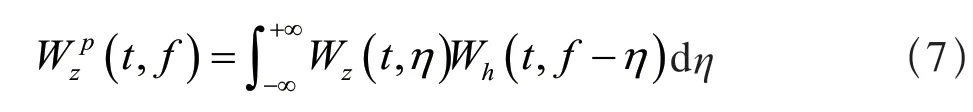
根據上式能夠得知，在時域加窗之后的結果與在頻域進行低通平滑濾波效果等同。如果再在頻域加一個窗函數，等同于在時域做卷積。兩個時域信號卷積后的WVD 等于各自WVD 在時間軸上的卷積，相當于對WVD 變換在時域做平滑。經過時域與頻域加窗處理后的WVD 稱為平滑偽維格納分布（SPWVD）。

式中，h(t)和g(t)是奇數長度的窗函數，滿足h(0)=1 和G(0)=1，G(f)為g(t)的傅里葉變換。

2 算法流程

本文提出的基于參數優化VMD 和SPWVD 的波磨辨識算法如圖2 所示，步驟描述如下：

圖2 軌道波磨辨識算法流程

（1）采集軸箱垂向振動信號，進行去除干擾及噪聲等濾波處理；

（2）將濾波后的振動信號進行參數優化的變分模態分解；

（3）選取信號的本征模態分量，計算波磨的特征值包絡譜熵；

（4）根據閾值判斷是否存在波磨；

（5）若采集的垂向振動信號，存在波磨，則對分解后的振動信號進行SPWVD 時頻分析，確定波磨中心頻率及波磨位置，計算波磨波長。

3 仿真分析

3.1 波磨仿真

軌道波磨能夠用一個近似余弦的信號來描述，為了更好地對軌道波磨進行仿真，本文進行4 種不同的波磨仿真實驗。鋼軌長度為40 m，采樣頻率為1 kHz，車速為10 m/s，一側軌道添加美國五級軌道垂向不平順（AAR5），另一側軌道在特定位置添加不同波磨，詳細的參數設置如表1 所示。

表1 軌道波磨參數設置

按照表1 所述參數，將軌道不平順數據制作成tre 格式的文件，導入SIMPACK 多體動力學軟件，并建立相應的軌道激勵函數，添加至列車仿真模型，然后分別完成速度、采集頻率、時間等一系列參數設置后，進行離線分析，保存軸箱振動的仿真結果數據，得到振動信號時域圖如圖3、圖4 所示，由圖可見，當添加的軌道波磨波深相同時，隨著波長的增加，軸箱垂向振動信號幅值呈現下降的趨勢。

圖3 僅添加AAR5的軸箱垂向振動時域

3.2 波磨故障辨識

由于仿真信號的振動數據不含有噪聲信號，故不再應用VSSLMS 方法進行濾波，直接采用參數優化VMD 方法進行模態分解，根據軸箱垂向振動信號的模態分解結果，計算分解后信號的包絡熵值，K、α參數值及包絡熵值，如表2 所示。

圖4 不同波長0.09 mm波深軸箱垂向振動時域

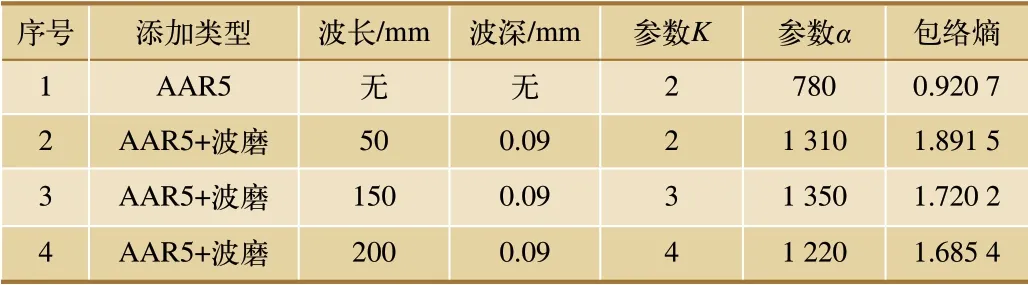
表2 軸箱垂向振動參數優化VMD的分解參數及信號包絡熵

由表2 中結果可知，僅含美國五級軌道譜的第一組包絡熵值為0.920 7，而其他添加軌道不平順的包絡熵數據遠大于第一組的值，因此，包絡熵可以作為軌道是否發生波磨的特征值，參考僅含美國五級軌道譜的包絡熵值，為留有一定的工程余量設置閾值為0.95，大于閾值判定為存在軌道波磨故障，反之則無軌道波磨故障。接下來為了進一步分析軌道波磨發生的位置及波長范圍，本文選取第4 組數據，用SPWVD 方法對分解后的垂向振動信號進行時頻分析，分析結果如圖5 所示。

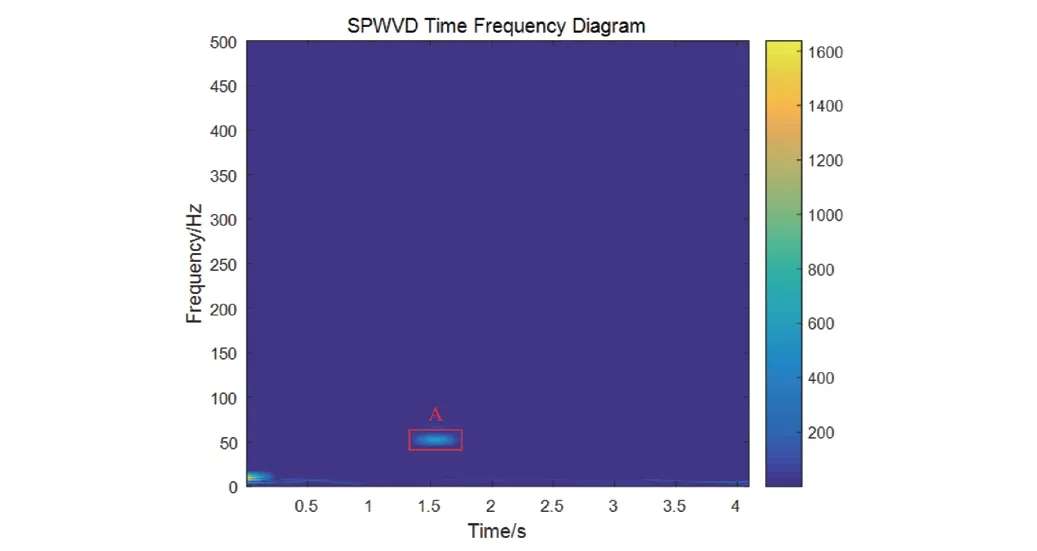
圖5 200 mm波長0.09 mm波深時頻

由圖5 可知，在A 處1.41 s ～1.69 s 時發生頻率集中，頻率范圍為[44.91 Hz 56.63 Hz]。時頻圖中零點起始位置也有頻率集中現象，但經過分析可知，此位置是由美國五級軌道譜所引起，并非添加軌道波磨所致。由于采樣頻率設置為1 kHz，根據波磨波長λ與振動頻率f的關系式可知：

式中，v為列車速度。

為了準確計算波磨波長，f取頻率集中區的中心頻率，計算可知，圖5 中添加軌道波磨的位置在14.1 m ～16.9 m，這與在15 m ～16 m 處的添加波磨位置基本穩合，波長為199.63 mm，與仿真200 mm波磨波長非常接近。

4 實例分析

為了進一步驗證波磨故障辨識算法的有效性，本節利用軌道波磨在線檢測系統設備，對廣州地鐵8號線的軌道線路進行檢測試驗，檢測列車運行速度為72 km/h，采樣頻率是10 kHz。本文截取一段1 km長度包含異常的軸箱垂向振動信號數據進行分析，其振動信號波形如圖6 所示。由圖6 可知，實測軸箱垂向振動信號中含有大量噪聲干擾，因此需要對采集的振動信號進行濾波處理，本文采用VSSLMS方法濾波，濾波后的波形如圖7 所示。

圖6 軸箱垂向振動信號波形（實測值）

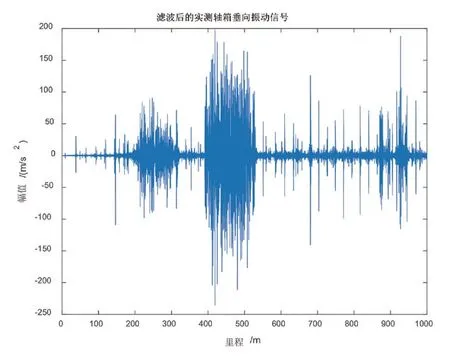
圖7 軸箱垂向振動信號波形（濾波后）

由圖7 可知，經過濾波后的軸箱振動信號在200 m ～300 m 及390 m ～530 m 處具有比較大的幅值波動，特別是在里程390 m ～530 m 處，不僅波幅大而且里程較長，并且從圖7 還可以看到較多的振動信號尖峰，分析可知，這是由于城軌車輛運行到鋼軌接頭處產生的沖擊力變化所致。

為了計算方便，本文截取350 m ～550 m 里程處的濾波振動信號進行數據分析，并且對此段數據5倍降頻處理，采樣頻率降為2 kHz，如圖8 所示。

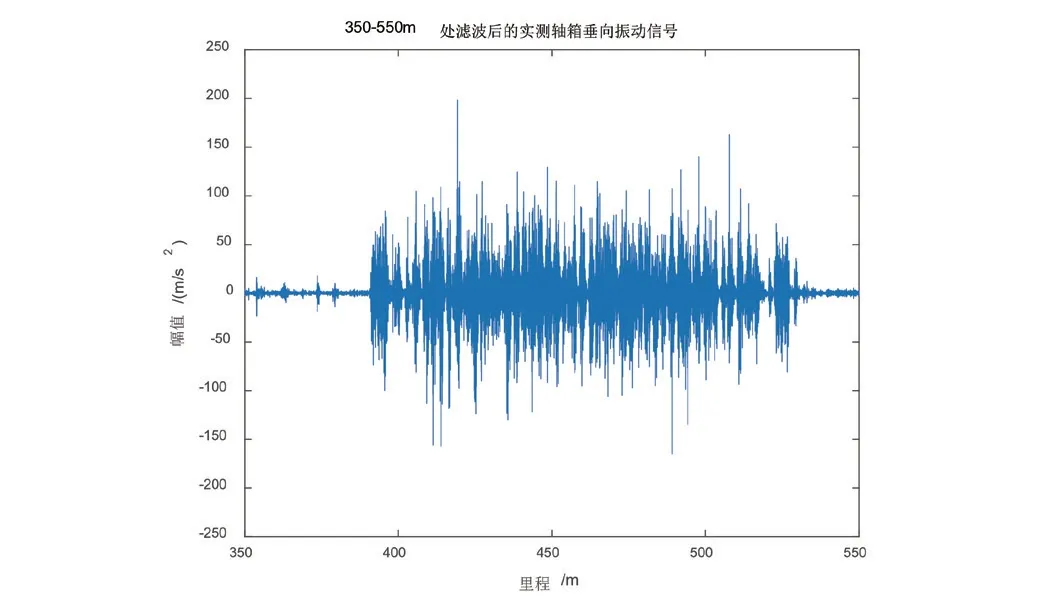
圖8 350 m～550 m處濾波后的實測軸箱垂向振動信號

在350 m ～550 m 里程處濾波信號經過參數優化的變分模態分解后，計算各IMF 分量的包絡熵為13.936，而這段軌道正常軸向振動的信號的包絡熵值為1.917，故可以判斷出該段軌道存在波磨。

為了進一步驗證檢測方法的有效性，在廣州地鐵工程人員的配合下，對440 m ～480 m 處軌道進行檢查，發現該段線路發生了如圖9 所示的波磨故障，從圖中可以明顯看到鋼軌表面發生了波浪形的磨耗，測量后得到該處軌道波磨的波長大致在76 mm 左右，與本方法檢測結果誤差最大僅為3.92%，從而驗證了本文所述方法對波磨故障檢測的有效性。

圖9 現場存在軌道波磨路段

5 結束語

本文通過采集環境激勵下列車軸箱上振動加速度傳感器的響應信號，利用變步長的LMS 自適應濾波方法對采集的加速度信號過濾作降噪處理，采用參數優化VMD 方法對信號進行分解，以分解信號的包絡熵為故障辨識指標，根據正常軌道的包絡熵設定閾值，識別軌道波磨，最后利用SPWVD 方法對含有波磨的振動信號進行時頻分析。具體結論如下：

（1）參數優化VMD 算法不僅克服了VMD 分解參數不能自適應選取的弊端，并且通過對比振動信號VMD 分解圖及各IMF 分量的時頻圖，充分說明了VMD 分解在關于抑制模態混疊方面的優越性；

（2）根據不同故障振動信號分解時包絡譜的差異，提出了以分解信號的包絡熵為軌道波磨辨識指標，通過設定故障閾值，識別軌道波磨；

（3）基于SPWVD 方法含軌道波磨振動信號進行時頻分析，根據分析結果，可以判斷出軌道波磨位置，并且利用波磨波長λ與振動頻率f的關系，能夠計算出波磨波長。