基于MedDRA系統的藥物安全性多重比較貝葉斯層次模型構建及應用*

東南大學公共衛生學院流行病與衛生統計學系(210009) 陳振明 李太順 楊嘉瑩 王詩遠 劉 沛

【提 要】 目的 在處理藥物不良事件的安全性分析時會面臨多重性問題，基于不良事件類型間的相似性，應用貝葉斯層次模型進行多重比較。方法 利用MedDRA詞典的層次結構構建貝葉斯層次模型，比較不同層次結構對模型的影響及其收縮作用。分析超過數概率進行統計推斷的優勢，以便標記出潛在的不良事件信號。結果 貝葉斯層次模型使得不良事件間的數據可以借用同一層次內的信息，達到收縮數據的作用，收縮的程度與層次結構有關。使用后驗超過數概率進行分析使得結果更具臨床意義。結論 本研究將貝葉斯層次模型引入不良事件的安全性分析中，并以實例說明其統計特性，為解決多重性問題提供了新思路。

藥物安全性數據的多重比較無論是對頻率統計還是貝葉斯統計都是較為棘手的問題之一[1]。藥物安全性數據常常包括眾多不良事件(adverse events，AEs)，而這些不良事件又因為分屬于特定器官和系統而存在著相關性，即需要在不滿足一般統計方法獨立性假定的條件下進行不良事件的多重比較。貝葉斯統計通過建立層次模型可有效處理這類復雜結構數據[2]。國外學者對此進行了深入研究，并取得了良好效果[3-4]。國內目前尚未見到這一方面的報道。究其原因，筆者認為可能與目前國內許多臨床試驗安全性數據結構不滿足構建貝葉斯層次模型的條件有關。隨著國家對臨床試驗數據標準化和電子化要求的提高，由人用藥物注冊技術要求國際協調會(international council for harmonization，ICH)開發的國際醫學標準術語—MedDRA引入了我國。MedDRA的標準化編碼和按臨床意義劃分的五級層次結構，為應用貝葉斯層次模型提供了條件。在此情況下，探討藥物安全性數據多重比較的貝葉斯層次模型構建具有現實意義。

原理與方法

1.MedDRA及層次結構

MedDRA是在醫藥事務管理活動中使用的一套醫學標準術語[5]，其編碼為五級層次結構，從低到高依次為低位語(lowest level term，LLT)、首位語(preferred term，PT)、高位語(high level term，HLT)、高位組語(high level group term，HLGT)、器官系統分類(system organ class，SOC)，它允許研究者從各種角度對數據進行檢索與歸類。以“流鼻涕”為例，對應的LLT編碼為“流鼻涕”，PT為“鼻漏”，HLT為“上呼吸道癥狀和體征”，HLGT為“呼吸道癥狀和體征”，SOC為“呼吸系統、胸及縱隔疾病”。由于SOC和HLGT主要按解剖學，生理學和病因學分類，所以在同一SOC或HLGT類別下的PT具有更高的相似性，這為構建貝葉斯層次模型提供了條件。

2.貝葉斯層次模型構建

令AEbj為第b個SOC類型下第j個PT發生的AEs，其中b=1,2,3…,b，j=1,2,3…,k；令Nt、Nc分別為Abj中試驗組(t)和對照組(c)的樣本含量，Ybj、Xbj為試驗組和對照組的AEs發生人數，相應的AEs發生率分別為tbj和cbj。按照Berry等[3]建議的方法構建三層次貝葉斯模型。

首先對Ybj，Xbj構建二項分布似然函數，即Ybj～Binom(Nt,tbj)，Xbj～Binom(Nc,cbj)。然后采用OR值作為比較指標，構建如下logistic回歸模型：

其中γbj是對照組的AEs發生率中率比的logit變換值，θbj為試驗組與對照組的logit差值增量，即log(OR)。顯然，θbj=0表示在不良事件類型AEbj中，試驗組與對照組的發生率無差別，即cbj=tbj。

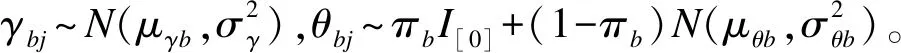
采用貝葉斯方法建立無效假設H0為OR=1，備擇假設H1為OR>1。如果OR>1的后驗概率大于0.5[7]，即H1成立的可能性大于H0，則接受H1，認為兩組間存在差異，試驗組AEs的發生風險高于對照組。反之若OR=1的后驗概率大于0.5，則接受H0。

3.超過數概率

本研究構建的層次模型不僅可以計算OR>1的后驗概率，也可以獲得其他感興趣參數的后驗概率，如OR>2。盡管OR>1表示試驗組的風險高于對照組，但不一定具有臨床意義。因此可以使用后驗超過數概率(exceedance probability)來標記不良事件信號，即P(ORbj>d*|data)>p[6]。d*和p的取值可以根據實際臨床意義進行界定，如d=1.5或2，p=0.5或0.8。p的取值越大，則需要的證據強度越大。

4.軟件實現及編程關鍵語句

根據上述原理，本文采用OpenBUGS、R軟件編寫計算程序。為構建貝葉斯層次模型，首先利用OpenBUGS語句：X[i]～ dbin(c[b[i],j[i]],Nc)，Y[i]～ dbin(t[b[i],j[i]],Nt)構建Ybj，Xbj的似然函數。每一個SOC層中的πb采用pi[k]～ dbeta(alpha.pi,beta.pi)構建，混合先驗部分先定義p0[i]～dbern(pi[b[i]])，然后根據示性函數選擇對應的概率分布，即theta1[b[i],j[i]]～ dnorm(mu.theta[b[i]],tau.theta[b[i]])，theta[b[i],j[i]]<-(1-p0[i])*theta1[b[i],j[i]]。若讀者需要完整程序，可直接聯系作者索取。

結 果

1.MedDRA分類及頻率統計分析結果

數據來源于筆者參與的b型流感嗜血桿菌(Haemophilus influenzae type b，HIB)疫苗III期臨床試驗，評價疫苗應用于2月齡至5周歲兒童的安全性和免疫原性。該試驗為非劣效的隨機對照試驗，分為2～5月齡、6～11月齡、1～5歲3個年齡亞組，選擇6～11月齡為分析對象，該組中試驗組、對照組人數各為250人。不良事件類型分布于代謝及營養類疾病，感染及侵染類疾病，呼吸系統、胸及縱隔疾病，皮膚及皮下組織類疾病，全身性疾病及給藥部位各種反應，胃腸系統疾病共6個系統。

對AEs的發生情況分別按照SOC/PT，HLGT/PT的層次結構進行編碼分類，試驗組和對照組的不良事件采用頻率統計的Fisher精確概率法進行假設檢驗，結果如表1所示。

由表1可知該研究共有6個SOC，14個HLGT，24個PT，最后一列給出了利用頻率統計的Fisher精確概率法得到的P值。其中兩組間差異存在統計學意義(P≤0.05)的AEs類型為上“呼吸道病毒感染”(P=0.042)和“嘔吐”(P=0.011)。若采用Bonferroni法對P值進行校正，P≤0.005，則所有的AEs都沒有統計學差異。

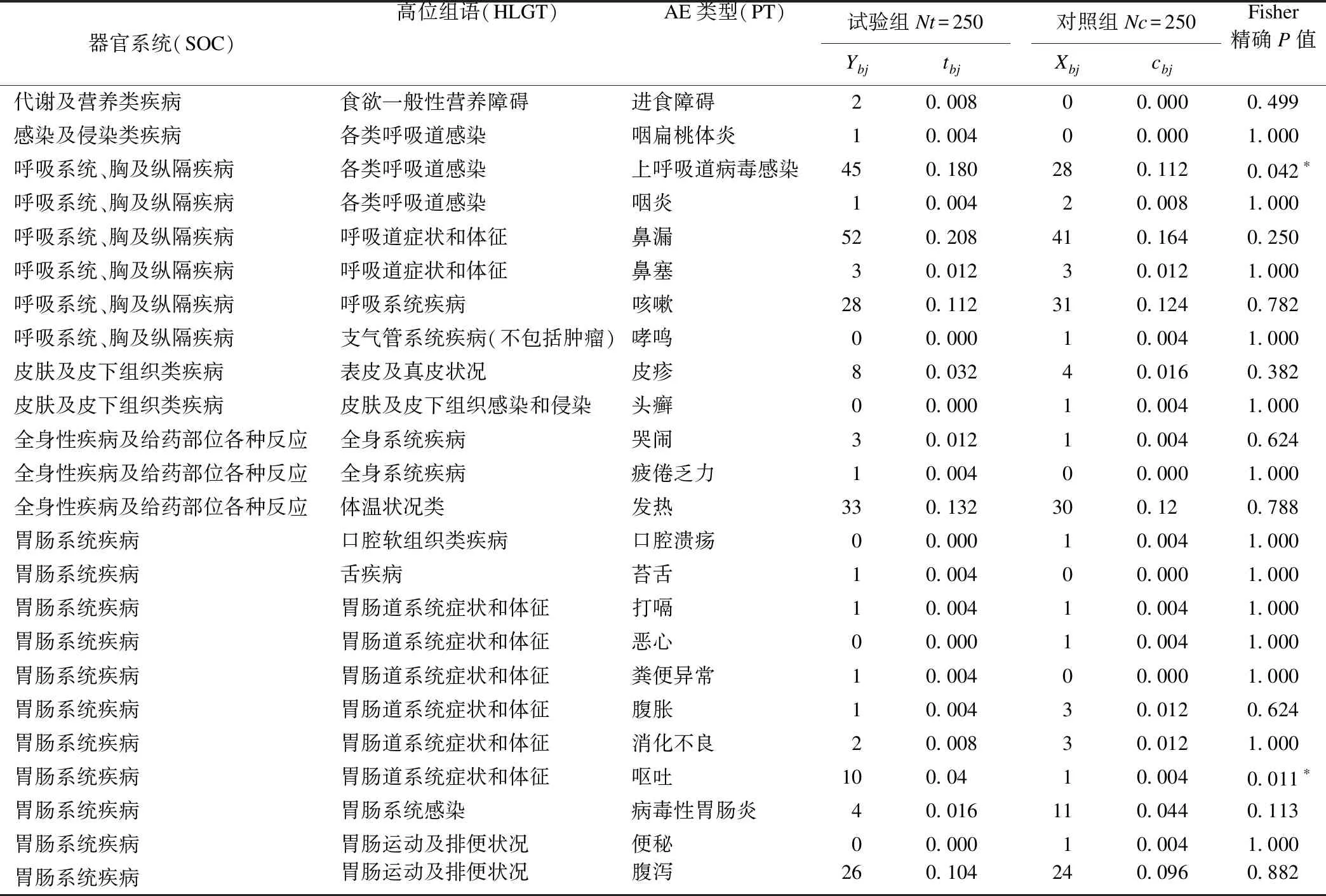
表1 HIB疫苗III期臨床試驗基于MedDRA分類的不良事件發生情況

*表示P≤0.05，有統計學差異。

2.貝葉斯層次模型分析

(1)后驗概率

按照SOC/PT、HLGT/PT間的層次結構得到各個AEs中OR=1和OR>1的后驗概率，如表2、表3所示。除了“嘔吐”，SOC/PT層次結構中其余AEs的P(OR=1|data)均大于0.5，即傾向于認為試驗組的不良事件發生率與對照組沒有差異。其中“嘔吐”的P值最小(0.004)，得到OR>1的后驗概率大于0.5(0.718)，即頻率統計和貝葉斯統計都認為組間存在差異。但不良事件“上呼吸道病毒感染”的P值小于0.05，得到OR>1的后驗概率卻小于0.5(0.231)，此時貝葉斯模型相比于Fisher精確概率法更傾向于認為“上呼吸道病毒感染”在兩組間沒有差異。

HLGT/PT得到的結果如表3所示，與SOC/PT得到的結論相似。相比于SOC，HLGT的層次劃分更為細致，它的層次結構更符合臨床概念，為此也更加合理。但由于層次更細會使得每一個HLGT下的PT數量減少，使得大部分HLGT下只有1個或2個PT，模型所帶來的收縮效果也會減小。

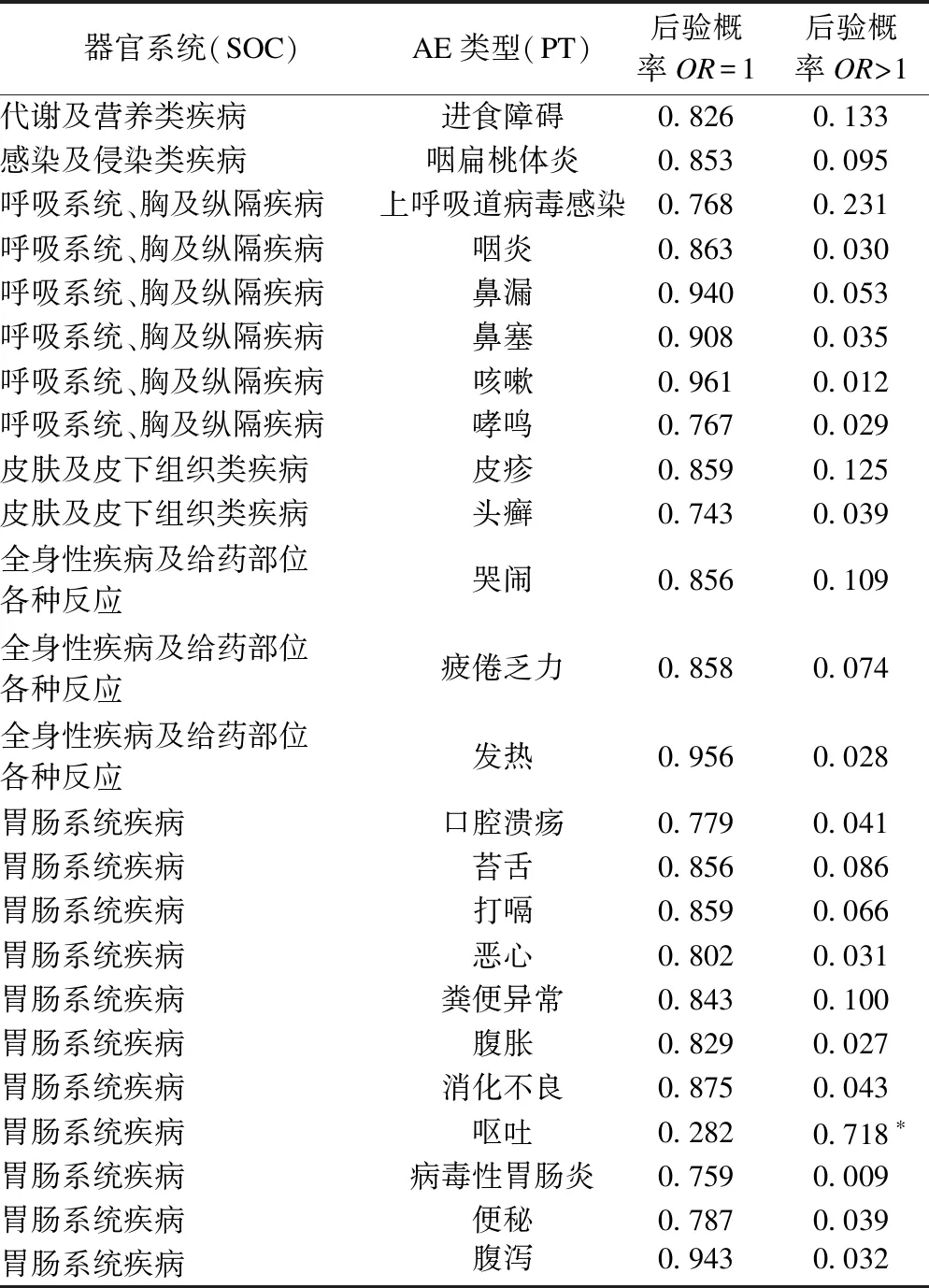
表2 HIB疫苗III期臨床試驗以SOC/PT為層次結構的貝葉斯后驗概率

*P(OR>1|data)>0.5，組間存在差異。

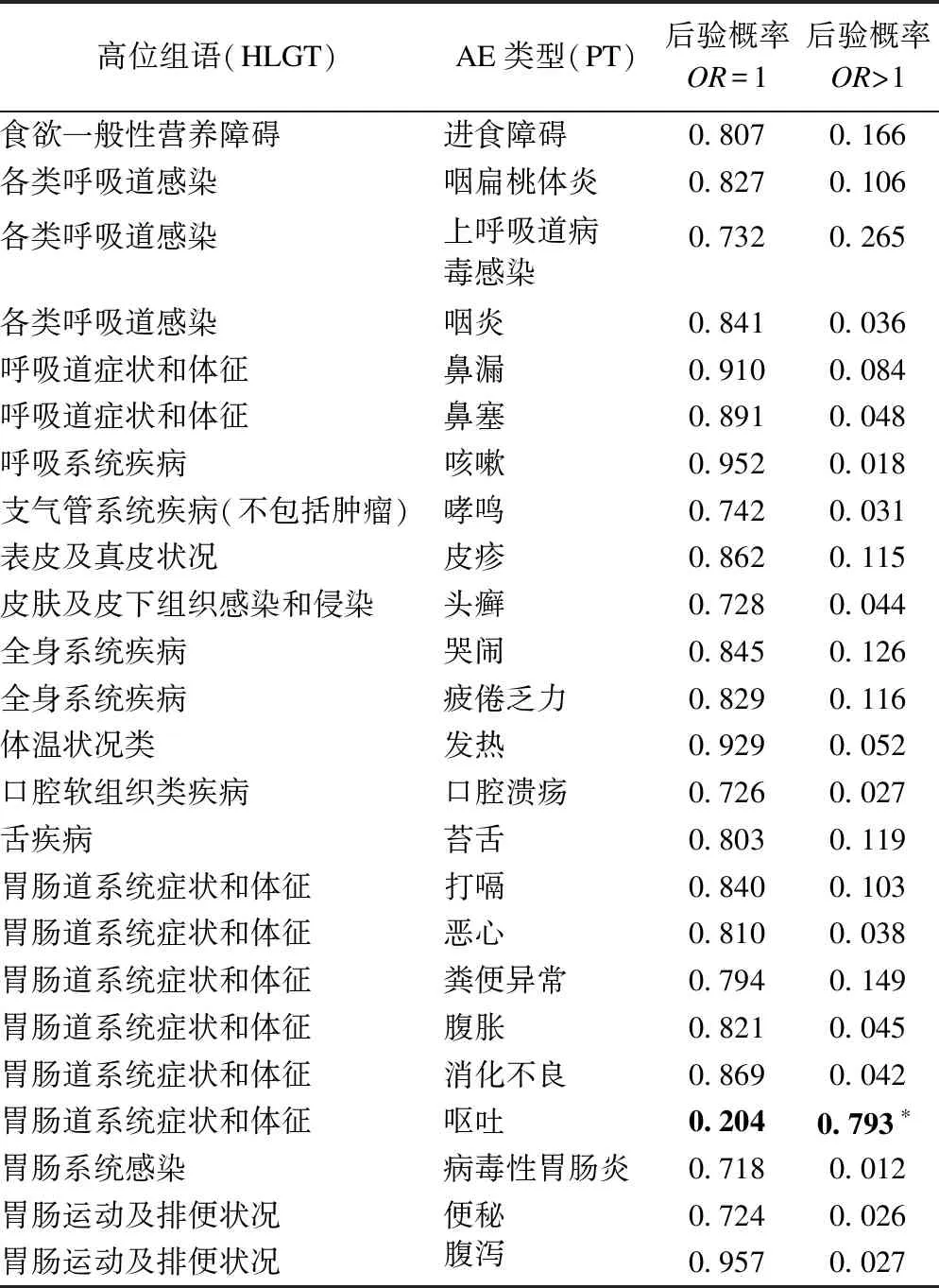
表3 HIB疫苗III期臨床試驗以HLGT/PT為層次結構的貝葉斯后驗概率

*P(OR>1|data)>0.5，組間存在差異。

(2)超過數概率

以該研究為例，在后驗超過數概率中分別取d*=1.5,d*=2，d**=0.02，d**=0.05，p=0.5比較SOC/PT、HLGT/PT中不良事件“上呼吸道病毒感染”、“嘔吐”的后驗超過數概率，如表4所示。隨著d*的增加，后驗概率逐漸下降，但下降的程度依據模型的層次結構而有所不同。如“嘔吐”，在SOC中P(ORbj>2|data)=0.676，而在HLGT中則為0.767。

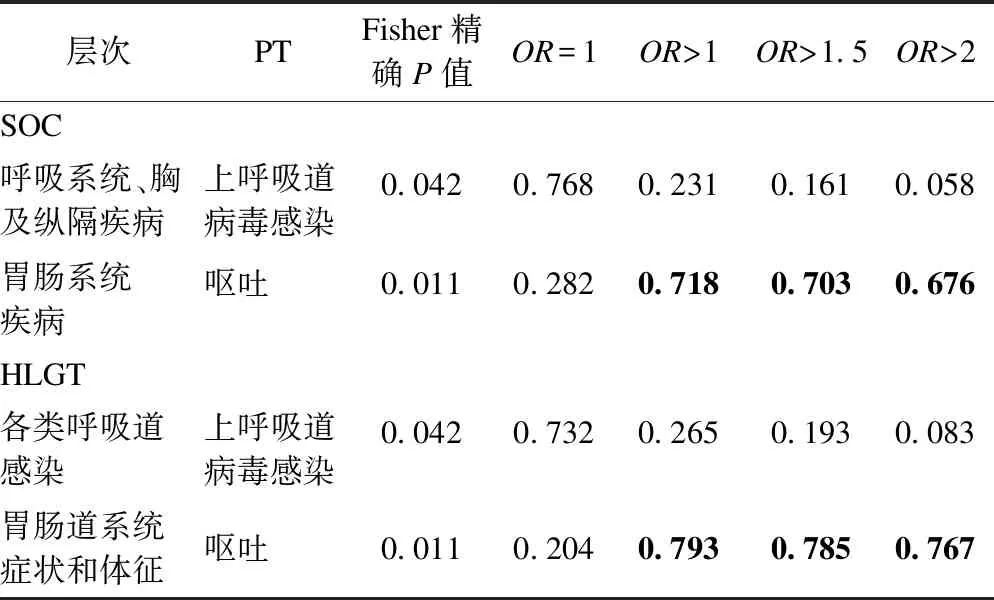
表4 不同層次結構的超過數概率

3.貝葉斯層次模型和頻率統計比較

無論是對頻率統計還是對貝葉斯統計，OR值及相應的可信區間都是進行安全性評價的重要統計推斷指標，圖1展示了用頻率統計與貝葉斯方法得到的SOC/PT、HLGT/PT中“上呼吸道病毒感染”與“嘔吐”的OR值結果。相對于頻率統計，貝葉斯統計得到的OR值更小，置信區間范圍也更窄。這一方面說明貝葉斯層次模型在安全性評價中的點估計結果沒有頻率統計那樣“激進”；另一方面說明貝葉斯層次模型在安全性評價中的區間估計結果比頻率統計更為精確。

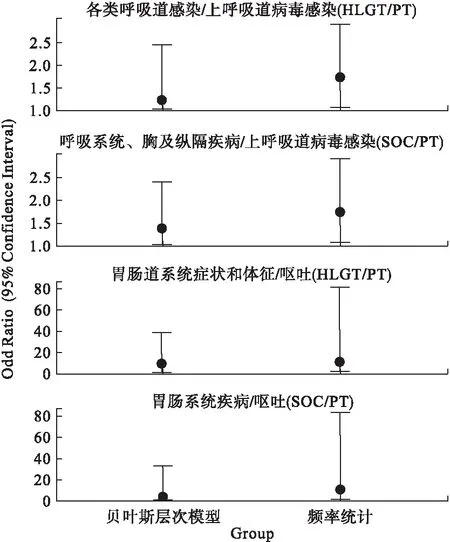
圖1 貝葉斯層次模型與頻率統計的OR值及其95%可信區間

討 論

在臨床試驗的安全性分析中，多重比較問題不可避免。在經典統計中，直接采用Fisher精確概率法進行假設檢驗容易導致假陽性。因此在處理這類問題時通常是采用Bonferroni法對P值進行校正，但當比較的類型增多時，過低的P值又會導致假陰性的增加。這樣的調整在樣本量較大的時候往往是比較保守的[8]，只有在極端情況下才能得到具有統計顯著性的結論。另一種方法是采用假發現率(false discovery rate，FDR)，將假/真陽性比例控制在一定范圍內以達到二者的平衡[9]。Mehrotra等人[10]基于這種方法，將不良事件按身體器官劃分，結合調整后的P值減少了多重性的影響。采用貝葉斯方法則可充分利用數據的層次結構信息，通過在相同層次內借用信息，進而提高統計推斷的效率。除了貝葉斯層次模型外，有研究者也提出了蒙特卡羅方法[11]與貝葉斯篩選方法[12]解決多重性問題。

本研究提示，對同一個不良事件采用貝葉斯層次模型和經典統計可能會得到不同的結果，如SOC/PT結構中的“嘔吐”。這是由于經典統計在計算P值的時候假定不同PT間AEs的發生是獨立的，而貝葉斯層次模型則認為“嘔吐”這一不良反應在其所屬的SOC/PT結構中并不獨立，通過引入與其它AEs的相關性使結果更符合臨床實際。本研究顯示，模型的層次結構不同，同一AE的后驗概率也有所不同。如“嘔吐”在SOC中的超過數概率低于HLGT，這說明模型層次可影響貝葉斯后驗概率，這一結果與Xia等人[6]的研究相同。

本研究另一值得關注的結果是，相對于頻率統計，貝葉斯統計得到的OR置信區間范圍更窄。這是因為貝葉斯層次模型將不同AE類型間的生物學聯系考慮在內，通過層次模型向平均水平的收縮提高了OR估計的精度[13]。這在某些亞組樣本含量較小或出現極端數據(0%或100%)時，其優勢更為明顯[14]。

相比于傳統方法僅檢驗OR是否等于1，本研究采用OR大于1的超過數概率作為安全性評價指標，有其獨到的優勢。顯然前者只能做出是否有風險的定性判斷，而后者則為研究者根據臨床實際同時進行定性和定量判斷提供了靈活的方法。如若某一不良反應危害較大(如出現血液系統損害)，則應給予較小的d*值以減少漏判，而對于危害較輕的不良反應則可給于較大的d*值。若對統計推斷的可靠性要求較高，則可以提高p的界值。研究者可以從臨床意義(d的大小)和統計推斷的可靠性(p的取值)兩個方面做出臨床決策。使用貝葉斯層次模型分析藥物安全性時，需注意其應用條件。模型要求隨機變量滿足可交換性，組內和組間的收縮基于數據服從獨立同分布假定，因此需要結合實際判斷數據是否滿足前提假設。