一類比估計量在數量特征敏感問題調查方法中的應用
李珊珊,劉 迪
(河套學院理學系,015000,內蒙古,巴彥淖爾)
0 引言
數量特征敏感問題調查方法的主要目的是估計敏感變量的均值或總值,例如調查員工平均額外收入多少,企業偷稅金額,學生作弊次數等。1969年Greenberg[1]提出了調查數量特征敏感問題的隨機化回答方法,Himmelfarb和Edgell[2]設計了加法模型,許多學者在一些經典模型的基礎上進行了研究,文獻[3]設計了一種數量特征敏感問題的改進模型;文獻[4]以Greenberg模型與加法模型為基礎提出了新模型,減少估計量的方差,提高了估計精度;文獻[5]在2種經典模型的基礎上給出了3種數量特征隨機化回答模型。金瑩[6]對2種經典模型作了改進,提出一種改進的Greenberg模型,提高了估計精度。
在直接調查中,通常利用與調查變量相關的輔助變量,借助輔助信息來提高估計敏感變量的精度。文獻[7]在2006年結合比估計提高了Warner模型的效率;文獻[8]在2007年使用了回歸分析提高了一般化隨機裝置的效率;文獻[9]提出雙輔助信息敏感性問題問卷調查技術;文獻[10]利用輔助信息提高屬性特征隨機化回答技術的效率。本文探討基于金瑩提出的改進的Greenberg模型,構造一類比估計量提高估計精度的問題。一類比估計量由Naik and Gupta[11]提出,包括均值、比估計、乘積估計、Srivastava(1967) 、Walsh(1970) 、Reddy(1973、1974)、Sahai(1979) 、Vos(1980) 、Adhvaryu和Gupta[12-19]提出的估計方法。通過理論推導和數值比較,在一定的條件下,提出的估計量提高了估計效率。
1 金瑩改進的Greenberg模型
金瑩[6]提出改進的Greenberg模型調查方法。
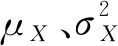
第2步:產生0-1分布的隨機數di,且P(di=1)=p。
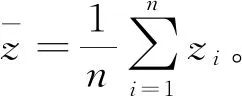
敏感性變量Y均值μY的估計量為
估計量的方差為
童話是屬于兒童文學范疇的一種特殊的文字表現形式,是為了適應小學生心理發展特點而構建的一個虛擬世界,伴隨在每位兒童的成長過程中。在實際教學中,為最大程度地發揮出童話的文學優勢,激發學生的學習熱情,保證童話課堂教學的有效性,教師可采用設置教學情境、拓展教學內容、組織課外活動等多種形式的教學方法,發揮童話的審美功能,進而激活學生的想象,豐富他們的情感體驗,帶領他們真正走進童話的世界。下面我就小學語文童話教學的三種策略展開探究。
2 改進的估計量
提出一類比估計量,用于改進的Greenberg模型。隨機化裝置盒中有外形相同的兩類卡片:1)敏感變量值Y,輔助變量值T;2)無關變量值X,輔助變量值T。
然后將卡片1)、2)以預定的比例p和1-p放入一個盒子中,回答者有放回地從盒中抽取卡片,并作出真實回答:(z1,t1),(z2,t2),…,(zn,tn)。
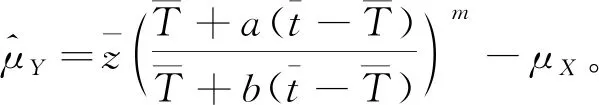
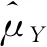
(1)
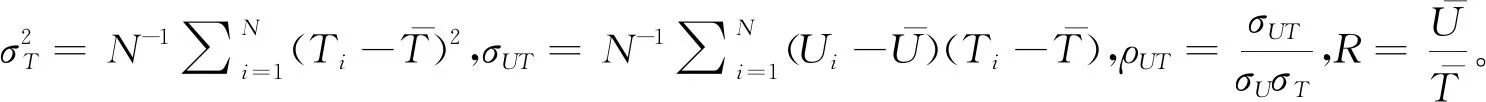
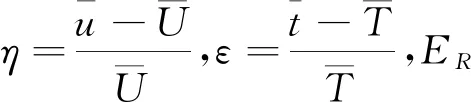
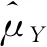
(2)
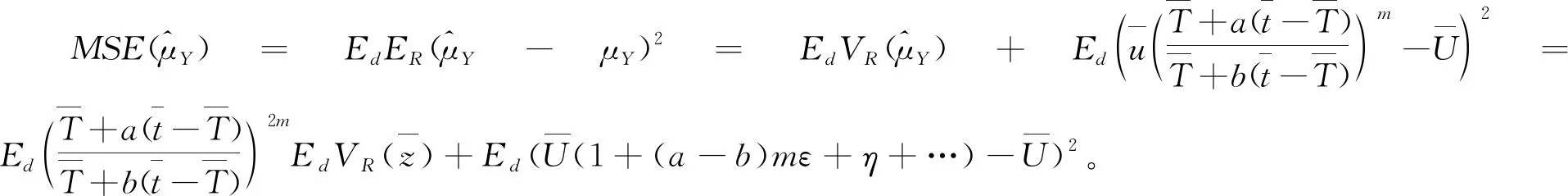
下面計算
綜上
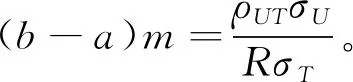
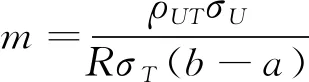
3 效率比較
3.1 比較估計量的偏差的大小
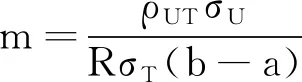
3.2 比較估計量的均方誤差的大小
當a,b,m取一些值時得到一些重要的估計,如表1所示。
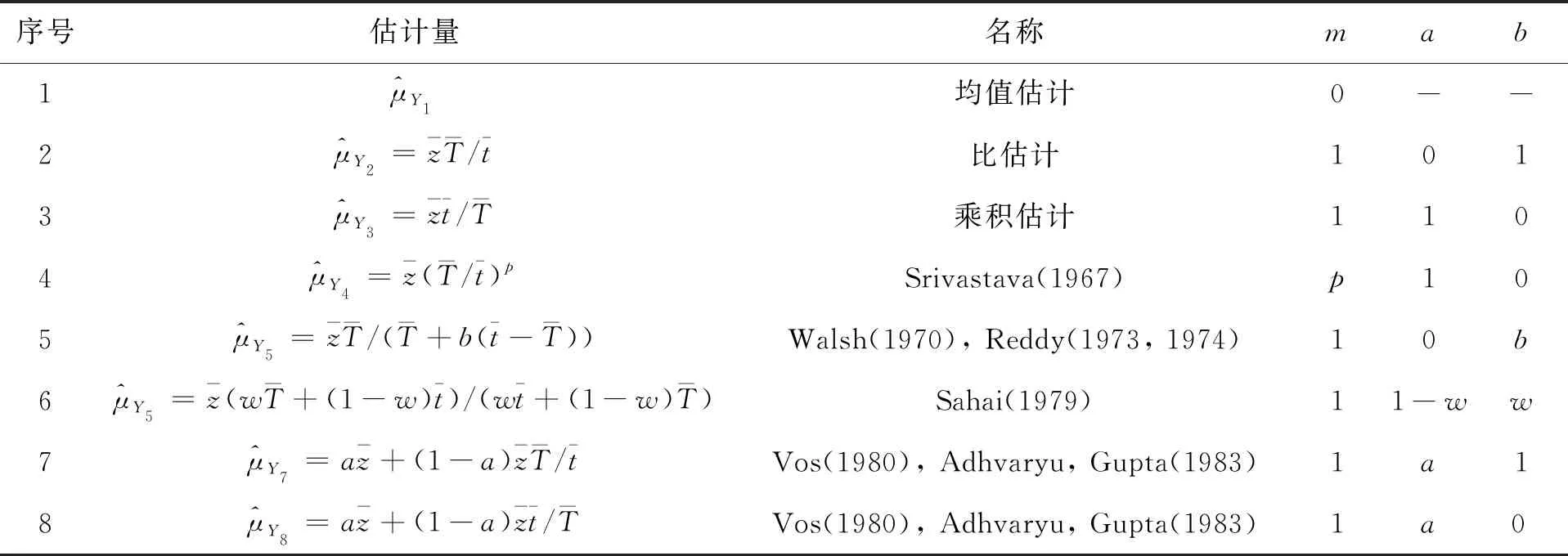
表1 提出的一類估計包括的估計量
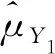
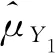
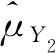
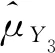
綜上可以得出如下結論。
1)當K≤-1時,2K+1<(b-a)m<-1。
2)當-1 3)當-1/2 4)當0 5)當1/2 6)當K≥1時,1<(b-a)m<2K-1。 通過以上結論,可以在實驗中根據不同值選擇不同的參數范圍。 K^μY1^μY2^μY3^μY4^μY5^μY6^μY7^μY81)0.340.531.705.820.190.190.190.198.882)-0.400.535.855.030.540.540.540.544.873)-0.140.212.011.200.180.180.180.180.904)0.240.632.056.540.280.280.280.289.77 從數值比較結果可以得出結論:利用輔助變量提出一類估計量的均方誤差在參數一定的條件下優于金瑩模型的效率,一類估計量中在參數不同的條件下包括7種不同的估計量,估計量的精度有所不同,再利用第3部分理論推導的結論,參數滿足(b-a)m=ρUTσU/RσT可以得到最優的估計效率,從表2中可以大致看出模型在參數滿足等式時的估計效率大致相同,而模型2)的效率較低的原因是因為選擇的輔助變量與敏感變量的相關系數為0.02,這也從側面驗證了選擇與調查變量無關的輔助變量時,不會提高估計效率。4 數值模擬
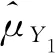

5 結論

