一種位置補償算法在伺服跟蹤系統中的應用

王 鑫，劉鑄華

(中國船舶重工集團公司第七二三研究所，江蘇 揚州225101)

0 引 言

在電子戰系統中，輻射源跟蹤是一個重要環節，而伺服跟蹤系統則是完成該環節的核心。隨著作戰對象機動速度越來越高、機動軌跡越來越多變，對伺服跟蹤系統的跟蹤速度和跟蹤加速度提出了更高的指標要求；同時，受限于電子戰系統的波束寬度指標，對伺服跟蹤系統的跟蹤精度也有了更高的要求。常規的應用場合下，比例積分微分(PID)算法和電流、速度、位置三環結構的結合，能一定程度上滿足伺服跟蹤系統對跟蹤準確性和快速性的要求[1- 2]。但是在某些遙控應用場合，網絡延遲會導致伺服跟蹤誤差加大，尤其是針對機動速度快、速度變化率高的目標，伺服跟蹤誤差會急劇增加[3]，甚至超過自身跟蹤波束寬度進而造成“跟丟”。

針對網絡延遲造成的伺服跟蹤系統跟蹤精度下降的問題，鑒于系統程序固化、PID 參數不便于動態調整情況[4]，本文采用位置補償算法。根據實際網絡延遲情況對遙控指令集進行外推，進而在保證伺服跟蹤系統固有的快速性和準確性前提下，提升了系統的動態跟蹤精度。

為了驗證算法的有效性，本文采用飛行體模擬軌跡，在大網絡延遲的環境中，對已有的伺服跟蹤系統進行半實物驗證，通過對比位置補償算法處理前后的系統跟蹤誤差曲線，可發現位置補償算法提升了伺服跟蹤精度，能夠滿足伺服跟蹤系統的使用需求。

1 伺服跟蹤誤差分析

在有網絡延遲的遙控應用場景，伺服跟蹤系統的指令-狀態鏈如圖1所示。

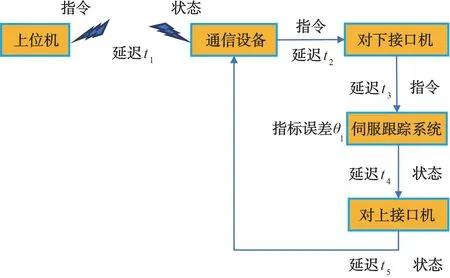
圖1 伺服跟蹤系統指令-狀態鏈示意圖

由圖1可見，遙控應用場景下的伺服跟蹤系統中，影響伺服跟蹤精度的因素包含以下各項：

(1)上位機指令通過無線網絡到通信接收設備的傳輸延遲t1；

(2)上位機指令通過通信設備，路經對下接口機到達伺服跟蹤系統的指令延遲t2和t3；

(3)伺服跟蹤系統在采用PID 算法和電流、速度、位置三環結構的情況下，系統固有的跟蹤誤差指標θ1；

(4)伺服跟蹤實時狀態傳遞到對上接口機及通信設備的網絡延遲t4和t5；

(5)伺服跟蹤實時狀態由通信設備無線傳輸到上位機的網絡延遲t1。

由于伺服跟蹤系統和上位機之間的狀態顯示同步，可以依靠時統來實現誤差消除，因此本文重點考慮(1)、(2)、(3)三項誤差影響因素。

飛行體的飛行軌跡是一個隨時間變化的時變函數，可以表示為s(t)。而伺服跟蹤系統的跟蹤曲線也是一個與時間、飛行體飛行軌跡有關的時變函數a(t)，可以表示為：

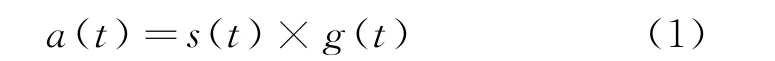
式中：g(t)表示伺服跟蹤系統的響應函數。

在采用了PID 算法和電流、速度、位置三環結構的伺服跟蹤系統中，系統跟蹤誤差可以表征為同一時刻下伺服編碼器反饋值與當前飛行體位置所決定的伺服指令值之間的絕對差e(t)，即：

而伺服跟蹤誤差指標θ1可以表示為：

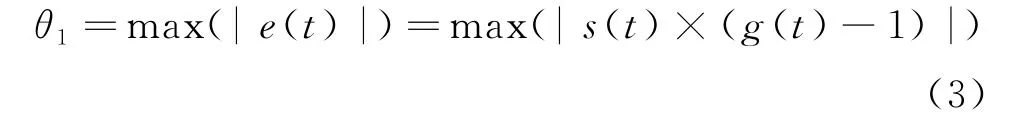
在考慮上述誤差影響因素(1)、(2)的情況下，當前時刻下伺服跟蹤曲線a(t)的輸入應該是帶上網絡延遲量后的輸入，因此在帶網絡延遲的應用環境下，伺服編碼器反饋值可以表征為：

此時的伺服跟蹤誤差是：

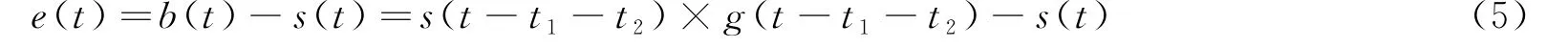
此時系統的跟蹤精度為：

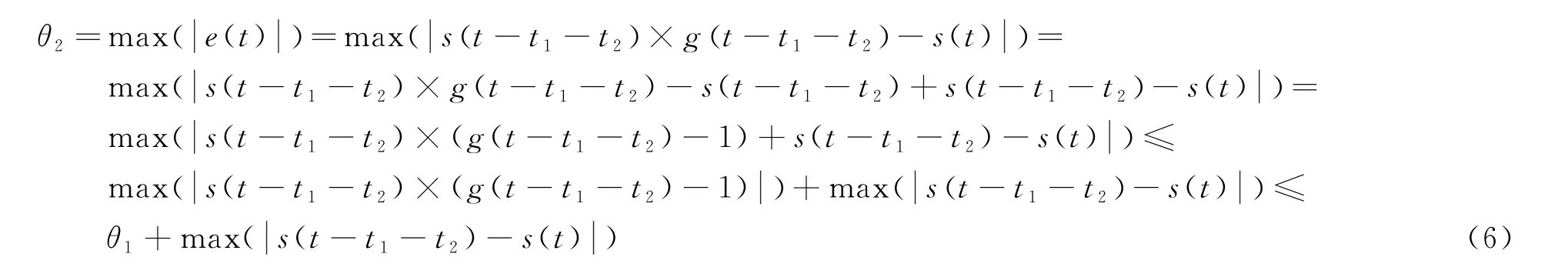
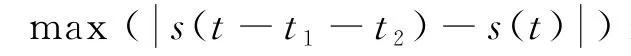
由式(6)可見，在有網絡延遲的遙控應用場景下，伺服跟蹤系統的跟蹤精度與系統固有指標能力θ1和飛行體自身的飛行角度變化率有關。當飛行體的角變化率較大時，伺服跟蹤系統的跟蹤精度對指令網絡延遲極為敏感[5]。

2 位置補償算法

在有線控制傳輸的應用環境下，系統的指令網絡延遲不大，θ1主要由系統固有的跟蹤誤差指標決定。由于執行動作相對于指令的滯后，θ1指標的提升主要依靠位置-速度-電流三環前饋的方式，進行系統能力優化。前饋控制系統原理如圖2所示。

圖2所示的位置-速度-電流三環控制系統，通過采用速度前饋補償，在加快伺服系統的速度響應同時，也減少了位置環對位置誤差的積分積累，從而改善因伺服動作滯后而引起的跟蹤精度下降。

圖2 伺服跟蹤系統前饋補償系統示意圖

在采用速度前饋補償算法以獲取伺服系統固有的高跟蹤精度θ1的前提下，本文主要分析因指令系統延遲造成的跟蹤誤差提升問題。

根據式(6)，要降低系統的跟蹤誤差，則需要降低s(t-t1-t2)-s(t)，鑒于飛行體軌跡不可預知，因此可以通過對伺服跟蹤系統接收到的s(t-t1-t2)進行位置補償，進而消除t1+t2延遲所帶來的跟蹤誤差影響。

由于數據率限制，傳遞到伺服跟蹤系統的目標位置函數s(t)是一個離散函數[6]，所以可以把接收到的目標位置指令表示為u(k)=s(t-t1-t2)，k=0、1、2、3…。網絡傳輸延遲時間t1+t2可以表示為Δ。位置補償算法的輸入為u(k)和延遲時間Δ，輸出表示為u︿(k+Δ)。當前時刻飛行體的真實位置是s(t)，經離散化后同樣可以表示為u(k+Δ)。故此，位置補償算法可以表示為：

將式(7)表示為輸入u(k)和延遲時間Δ的表達形式：

式中：g(Δ)表示位置補償量，根據公式(8)，有：

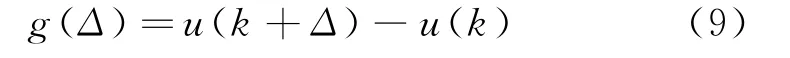
根據實際作用對象，可以對飛行體飛行軌跡進行最小二乘擬合，即：

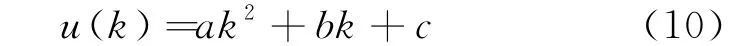
上式可以通過歷史軌跡點u(k)、u(k-1)、u(k-2)進行實時求解。通過式(8)、(9)、(10)，可得到：

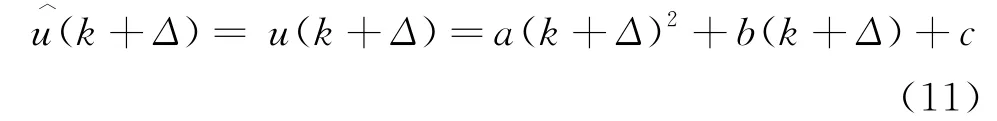
由式(11)，位置補償后的目標位置指令由歷史軌跡點u(k)、u(k-1)、u(k-2)、網絡延遲Δ計算得到。其中Δ可通過時統計算：Δ=伺服系統接收指令時刻-指令上時標。

3 仿真驗證

針對位置補償算法，采用現有一套高精度伺服跟蹤系統進行算法驗證，在采用了速度前饋設計的前提下，伺服跟蹤系統的固有動態跟蹤精度指標為0.5°。飛行體軌跡為虛擬飛行軌跡，時長20 s，最大角變化率為2.5°/s，最大角加速度變化率為5°/s2。虛擬通信設備延遲量500 ms，時統精度1 ms，指令傳輸頻率10 Hz，狀態反饋頻率1 Hz。半實物仿真架構如圖3所示。

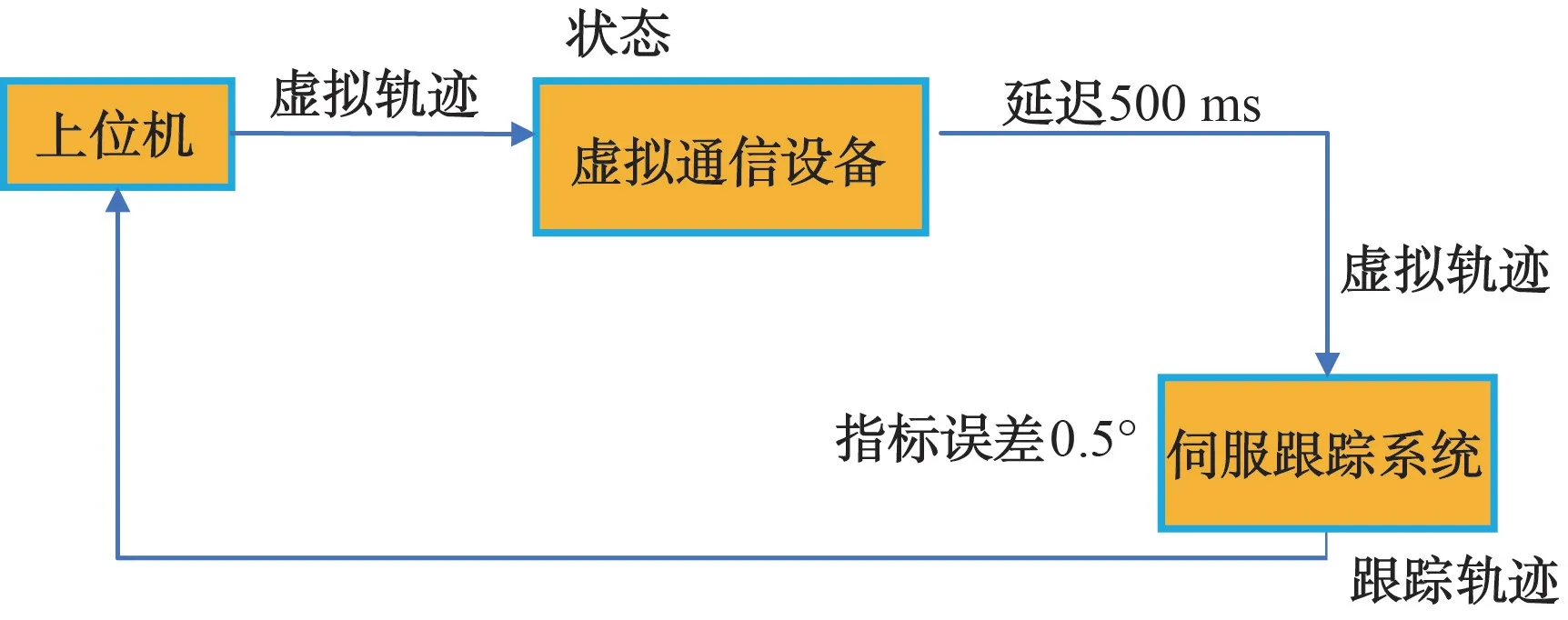
圖3 位置補償算法半實物仿真驗證示意圖

圖4分別是使用位置補償算法前后，伺服跟蹤系統跟蹤曲線與飛行體理論飛行軌跡的對比圖。

圖4 算法補償前后伺服跟蹤曲線與理論飛行曲線對比圖

從圖4可見，位置算法補償前，實際指向和理論指向的最大偏差值表征了伺服跟蹤精度，其精度為1.34°，這與常規采用速度前饋設計的伺服跟蹤指標1°相差較大，主要原因是指令傳輸延時過大，已經較大地影響了伺服跟蹤系統的精度指標。在采用位置算法補償后，伺服跟蹤系統實際指向與理論指向的最大偏差值為0.45°，與伺服跟蹤系統固有的0.5°跟蹤精度指標一致。

4 結束語

本文對有指令延遲條件下伺服跟蹤精度的誤差影響因素進行了分析，理論分析結果表明，該條件下伺服跟蹤精度只跟網絡延遲時間、伺服跟蹤系統固有跟蹤精度指標有關，進而提出了針對控制指令的位置補償算法。半實物仿真結果表明，該算法對網絡延遲環境下的伺服跟蹤系統具有明顯的跟蹤精度提升作用，能夠滿足一定條件下的伺服跟蹤使用需求。