一種計及無功補償的分布式電源優化配置方法
張 潮,陳 靜,顧衛祥
(1.南京工程學院,江蘇省南京市 211167;2.新疆阜康抽水蓄能有限公司,新疆維吾爾自治區阜康市 830011)
0 引言
集中式發電和分布式發電相互補充是未來電網的發展趨勢[1],對現有的配電網進行改造和接入分布式電源(Distributed Generation,DG)是改善能源結構、提高能源利用率的有效途徑。DG的配置問題對系統的經濟可靠運行具有重大影響,合理的位置接入合適容量的DG可以有效改善系統電壓水平、降低系統網絡損耗、提高系統可靠性[2~5],因此對DG選址定容問題的研究具有迫切性和必要性。
目前,針對DG的選址定容問題已經受到國內外學者廣泛關注,文獻[6~9]利用傳統的數學方法包括梯度法、二次規劃法、牛頓法和內點法對DG選址定容模型進行求解,這類方法有著嚴格的數學定義,對求解復雜的數學模型并不適用。近年來隨著配電網結構復雜化、精細化,DG的規劃中也需要建立復雜數學模型,各種智能啟發式算法以其優越的非線性尋優能力被廣泛應用在求解DG優化配置問題。文獻[10~14]從不同優化目標出發,分別利用遺傳算法、螢火算法、粒子群算法、蟻群算法、貓群算法對分布式電源接入配電網的配置進行優化,通過仿真算例證明在不改變電網架構的情況下,通過合理配置分布式電源可以有效改善配電網運行情況。
上述針對DG選址定容問題的研究提供了很多開創性思路,但同時也存在著一些問題。
(1)在實際工程中,DG接入配電網往往需要與儲能系統配合布置,以提高配電網對可再生能源的消納能力,這一方面已經成為當下的研究熱點,已有文獻對此研究仍顯不足。
(2)隨著大量出力呈現隨機概率分布的DG接入配電網,配電網需要更多的無功補償設備以維持系統電壓穩定,所以在DG的規劃過程中考慮無功補償設備的配置顯得尤為重要。
基于以上分析,本文在DG配置過程中,考慮無功補償設備的配置,提出DG與儲能協調配合下的DG配置優化模型,從經濟成本和技術性指標考慮,建立了DG、儲能系統、無功補償設備建設成本最小,系統網絡損耗最小,系統電壓穩定指標最優的多目標優化模型,并提出一種基于概率分布策略的改進遺傳算法,將該算法應用于求解DG的優化配置模型。
1 優化配置模型
系統網絡損耗和系統電壓穩定指標VSI同屬于技術指標,采用加權組合優化,目標函數為F2。
分布式電源優化配置目標函數如下:

式中:F1經濟成本函數,F2為技術指標函數。
1.1 經濟成本
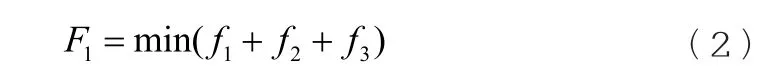
式中:F1為項目投資期內的總經濟成本;f1為分布式電源建設成本;f2為儲能系統建設成本;f3為無功補償設備建設成本。
(1)分布式電源建設成本。
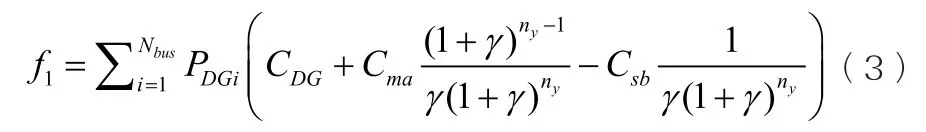
式中:Nbus為配電網節點數;PDGi為第i節點接入DG的有功功率;CGD為DG單位有功功率投資成本;Cma為DG單位有功功率維護成本;Csb為DG單位有功功率回收殘值;γ為貼現率;ny為項目運行周期,為等年值求現比率;為將來值求現比率。
(2)儲能系統建設成本。
本文考慮儲能系統與DG協調運行,只在DG接入點配置儲能系統,其配置既考慮DG的有功出力的轉換成本,也考慮故障情況下短時間內維持接入點重要負荷繼續運行的要求。
式中:fcn_inv為儲能系統初始投資成本;fcn_ma為儲能系統維護成本;fcn_rc為儲能系統置換成本;fcn_cp為儲能系統報廢處理成本。
其中:
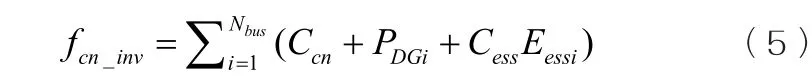
式中:Ccn為儲能系統單位有功功率轉換成本;Cess為儲能系統單位容量投資成本;Eessi為第i節點接入儲能系統的容量。
由于儲能系統中儲能單元運行周期小于分布式電源項目運行周期,需要在儲能系統中考慮儲能單元的置換成本fcn_rc。
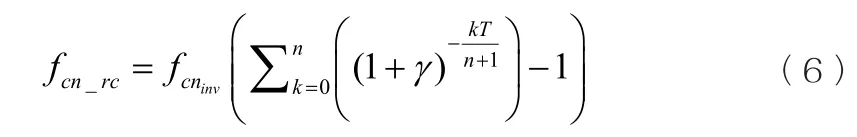
式中:n為置換次數;T為運行周期。
為簡化模型,儲能系統維護成本fcn_ma、儲能系統報廢處理成本fcn_cp均按初始投資成本的一定比例進行計算。
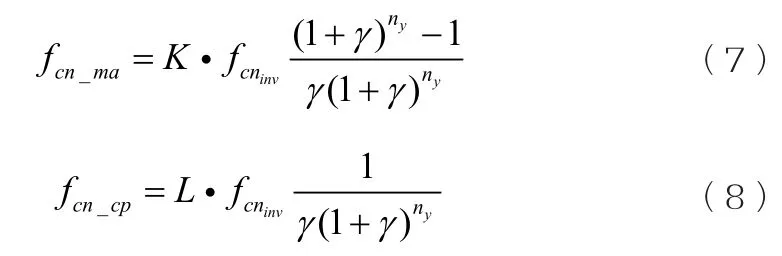
式中:K為維護成本占初始投資的比例;L為報廢處理成本占初始投資的比例。
(3)無功補償設備建設成本。
本文在配置并聯電容器組等靜態無功補償裝置的基礎上通過配置SVG以實現DG出力波動或故障情況下對配電網進行有效調壓。并聯電容器組與DG同時進行選址定容,SVG根據有功損耗對節點補償無功的靈敏度選取位置[15]。

式中:fwg_c為并聯電容器組建設成本;fwg_svg為SVG組建設成本。
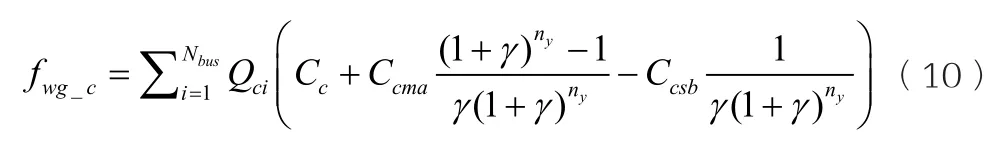
式中:Qci為第i節點接入并聯電容器組的容量;Cc為并聯電容器組單位容量投資成本;Ccma為并聯電容器組單位容量維護成本;Ccsb為并聯電容器組單位容量回收殘值。
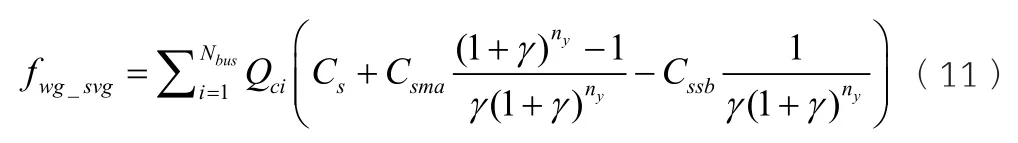
式中:Qsi為第i節點接入SVG的容量;Cc為SVG單位容量投資成本;Ccma為SVG單位容量維護成本;Ccsb為SVG單位容量回收殘值。
1.2 技術指標
(1)網絡損耗。

式中:Ploss為配電系統網絡損耗;l為系統支路數;rk為系統k支路電阻;Ik為系統k支路通過的電流。
(2)電壓穩定指標。
DG接入配電網后也會改變相應節點的電壓水平,若DG接入方式不當,極易造成系統電壓失穩[16],文獻[16]提供了計及分布式電源接入的配電網電壓穩定性評估指標VSI,定義節點j的VSI為:
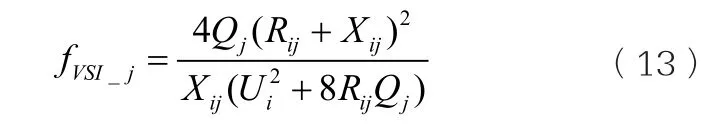
式中:fVSI_j為節點j的VSI;Qj為節點j送出的無功功率;Rij+Xij為線路ij的阻抗。
本文定義配電網的VSI為所有節點VSI的最大值,即fVSI。

故兩者加權組合優化函數為:
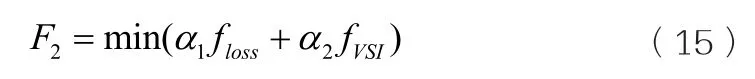
式中:α1為網損權值;α2為配電網的VSI的權值;α1+α2=1。
1.3 約束條件
(1)功率平衡約束。
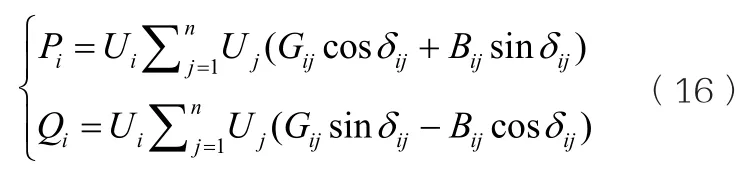
式中:Pi、Qi為節點i向系統注入的有功功率、無功功率;n為系統的節點數;Ui、Uj為節點i、j電壓向量的幅值;Gij為節點導納矩陣元素Yij的實部;Bij為節點導納矩陣元素Yij的虛部;δij=δi-δj,為i、j兩節點電壓的相角差。
(2)電壓約束。

式中:Umin和Umax為節點電壓允許的上下限,一般電壓正、負偏差的絕對值之和不超過額定值10%。
2 多目標遺傳算法
2.1 遺傳算法基本原理
遺傳算法(GA)具有魯棒性好,計算復雜度低,需要目標
函數的參數少等優點[17~19]。應用遺傳算法進行優化主要包括5個步驟:初始化種群、構造適應度函數、選擇操作、交叉操作、變異操作。
(1)初始化種群。
依據算法設定的參數,對種群進行初始化,內容包括DG的位置和容量、無功補償設備的位置和容量四部分。
(2)構造適應度函數。
根據種群內個體信息構建分布式電源配置模型,以技術指標和經濟指標作為評價種群內個體優劣的指標,即個體的適應度F。
(3)選擇操作。
本文采用輪盤賭策略選擇種群中的個體,即基于種群中個體的適應度大小決定個體選擇概率,計算公式如式(18)、式(19)所示。
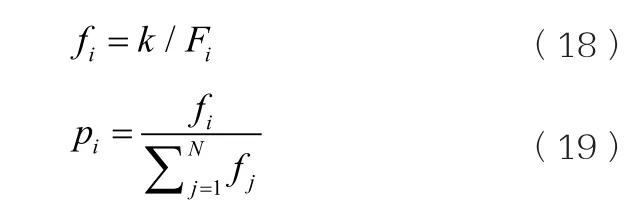
式中:Fi為種群中第i個個體適應度;k為系數;由于適應度值越小越好,所以以fi取代Fi,pi為個體被選中的概率。
(4)交叉操作。
本文交叉策略采用實數交叉法,假設第m個個體am和第n個個體an在第j個位置進行交叉,其操作過程如式(20)所示。
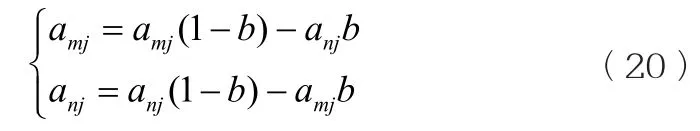
式中:b為0,1之間的均勻分布的隨機數。
(5)變異操作。
假設第i個個體的第j個部分aij發生變異,其操作過程如式(21)所示。
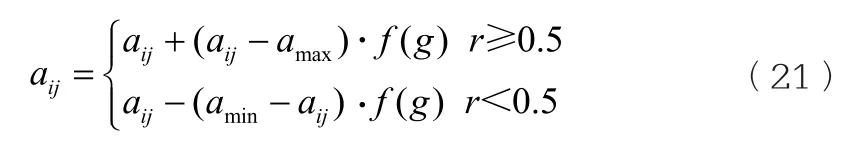
式中:amax、amin為aij的上下界;r為0,1之間的均勻分布的隨機數。
其中,算法變異操作采用下式:

式中:r2為[0,1]之間的隨機數;g和Gmax分別為當前迭代次數和最大迭代次數。
2.2 改進遺傳算法
通過式(20)和式(21)可以看出,基本的遺傳算法交叉、變異操作針對所有個體執行,在算法后期,極有可能因個體交叉,變異不當,導致算法收斂速度變慢,存在精度不高的問題。在本文算法中,將保留每一代種群中適應度最高的個體不參加交叉、變異,其余個體按照概率μ進行交叉、變異操作,概率公式按式(23)計算。
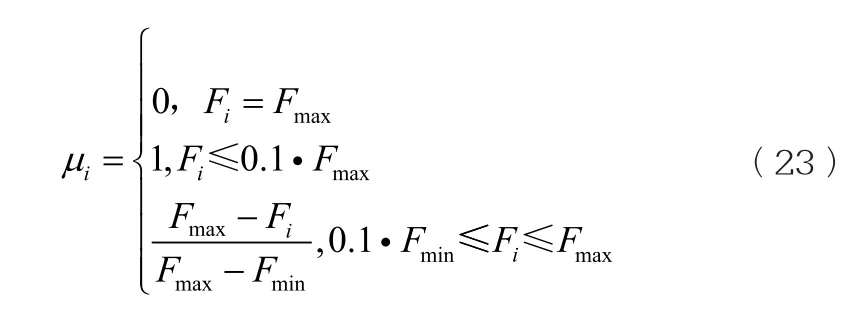
式中:μi,Fi為個體i進行操作的概率及適應度值;Fmax,Fmin個體適應度得最值。
當滿足μi>rand時,個體進行交叉、變異操作,rand為[0,1]之間隨機產生的數。算法流程如圖1所示。
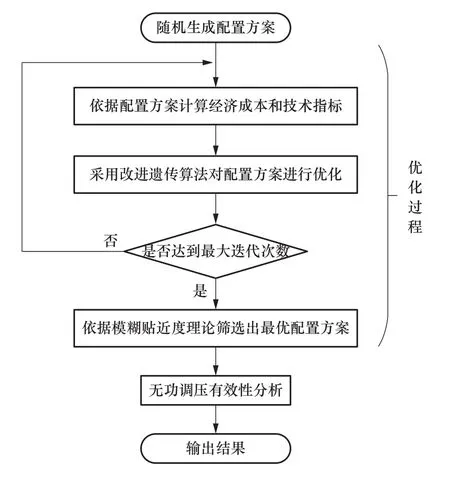
圖1 算法流程圖Figure 1 Flow chart of algorithm
3 算例分析
本文選取IEEE-33節點配電系統為研究對象。未接入分布式電源時系統初始網絡損耗和電壓穩定指標分別為202kW和0.1363,為避免網絡損耗和電壓穩定指標因數量級差別導致誤差,分別以與各初始值的比值作為優化指標進行加權,分布式電源均視為PQ節點,其功率因數為0.9。
3.1 參數設置
分布式電源在規劃時,分布式電源投資成本為12500元/kW,維護成本為2000元/kW,回收殘值為650元/kW,項目周期為20年,貼現率為6.7%[3][11];儲能功率轉換成本為2142元/kW,儲能容量設置為保證接入點負荷2小時供電[20],容量投資成本2210元/kWh,維護比例K為10%,報廢處理比例L為5%,設備使用年限為8年[20][21];電容器組投資成本為60元/kvar,維護成本為10元/kvar,回收殘值為10元/kvar,SVG容量投資成本為250元/kvar,維護成本為20元/kvar,回收殘值為20元/kvar,設備使用年限為 25 年[22],。
算法設置中,種群大小為100,存儲檔案大小為70,最大迭代次數為100,從2~33節點中選取5個位置安裝分布式電源,1個位置按照電容器組,根據有功損耗對節點補償無功的靈敏度選取SVG安裝位置。
3.2 多目標優化結果及分析
根據本文提出多目標優化模型,按照改進MALO算法進行求解并與原始MALO求解結果進行對比,結果如圖2所示。
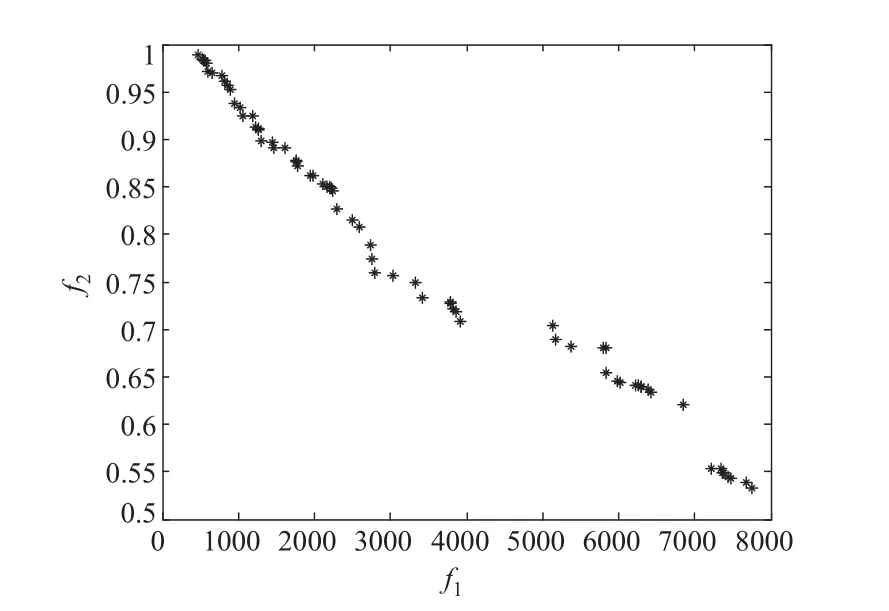
圖2 非劣解分布情況Figure 2 The distribution of the pareto solutions
采用文獻[22]中的模糊貼近度對非劣解集進行篩選,得到的最優配置方案如表1~表3所示。

表1 DG配置方案Table 1 Allocation scheme of DG

表2 儲能系統配置方案Table 2 Allocation scheme of energy storage system
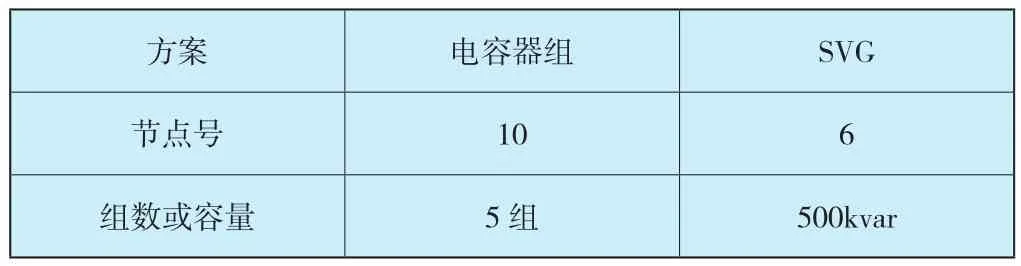
表3 無功補償設備配置方案Table 3 Allocation scheme of reactive power compensation equipment
表2中,儲能系統的容量按照在DG退出運行后,保證接入點負荷2小時供電進行規劃[20]。
表3中,電容器組每組容量為15kvar,在有功損耗對節點補償無功的靈敏度較大的6號節點接SVG,參考文獻[15]實例分析,選擇接入容量為500kvar較為合適。
按照上述配置結果,將DG、儲能系統和無功補償設備接入IEEE-33配電系統,結果如圖3和表4所示。
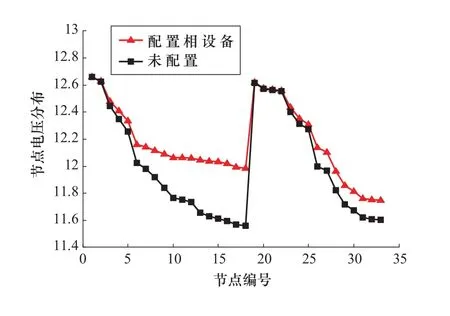
圖3 電壓分布Figure 3 Voltage distribution

表4 技術指標Table 4 Technical indicators
3.3 無功設備調壓有效性分析
為了驗證本文提出的無功設備配置的有效性,采用上述規劃結果,針對最極端情況進行分析:DG因故障退出運行。
假設3、13號節點DG退出運行,采用無功設備優化電壓分布,結果如表5和圖4所示。

表5 無功設備參數Table 5 Parameters of reactive power compensation equipment
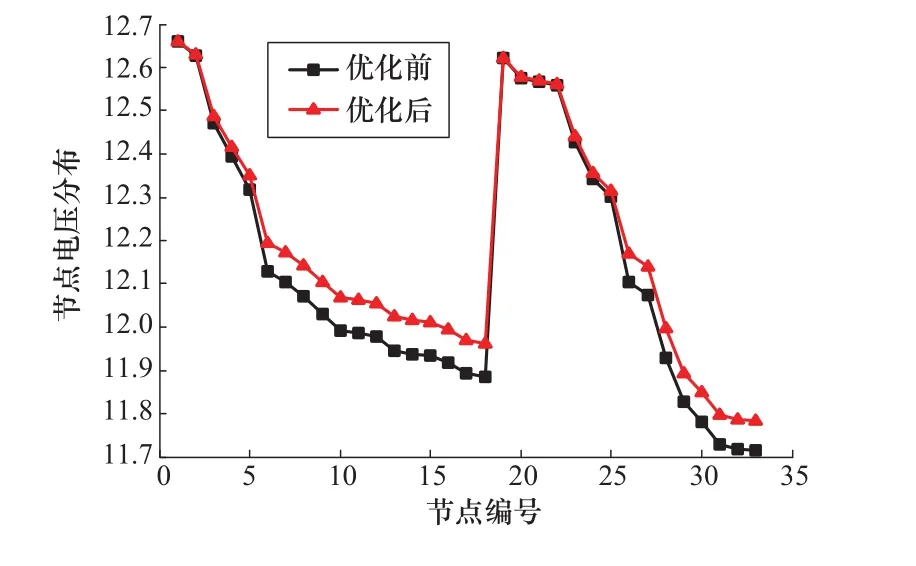
圖4 優化前后電壓變化Figure 4 Voltage change before and after optimization
由圖4可以看出,部分DG退出運行后,系統局部電壓水平發生惡化,本文通過設置無功補償設備可以有效改善局部電壓水平。
4 結論
本文考慮儲能與DG配合布置,無功設備參與選址定容,建立了DG、儲能系統、無功補償設備建設成本最小,系統網絡損耗最小,系統電壓穩定指標最優的多目標數學模型,并應用改進遺傳算法求解該模型,分析表明。
(1)改進多的遺傳與原算法相比,有效地避免了算法在中后期陷入局部最優,具有更高的精度。
(2)DG配置過程中,考慮儲能系統與DG協調配合的優化模型,更符合當前工程實際,其接入配電網,可以改善配電網運行狀況,提高系統穩定性。
(3)DG配置過程中,考慮無功補償設備的接入可以在配電網原有無功不足情況下,應對DG出現出力波動或故障時電壓惡化的狀況,在保證系統穩定運行的情況下,提高DG利用率,實現DG就地消納。

