基于多前車最優速度與加速度的網聯車跟馳模型

史昕 紀藝 趙祥模 惠飛

摘? 要： 考慮車輛跟馳存在的延時性與傳遞性，基于網聯車的智能感知與協同交互，提出一種基于多前車最優速度與加速度的網聯車跟馳模型，并利用線性穩定性分析方法推導所提出模型的臨界穩定性判別條件。以環形道路車隊過程施加擾動為例，根據加速度敏感系數[ωi]和多前車數[k]設計數值模擬實驗，結合速度和車頭距等參數分析不同[ωi]和[k]取值條件下的車隊行駛穩定性。模型穩定性分析表明，所提出模型在引入多前車最優速度與加速度項后，具備更優的穩定區域，且考慮前車數[k]越多、加速度敏感系數[ωi]越大，則模型的穩定性越好。數值模擬分析表明，所提出模型相比FVD，OVCM和MHOV模型，當加速度敏感系數[ωi]和前車數[k]取值合理時（[ωi=0.3]且[k=4]），車隊速度和車頭距的波動幅度相對較小，由此說明所提出模型能較好地吸收擾動且有利于增強車隊行駛穩定性。

關鍵詞： 網聯車跟馳模型; 多前車最優速度與加速度; 臨界穩定性判別; 模型穩定性分析; 數值模擬分析; 擾動吸收

中圖分類號： TN92?34? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼： A? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號： 1004?373X（2020）09?0135?06

Car?following model of connected vehicles based on

multiple optimal velocities and accelerations

SHI Xin， JI Yi， ZHAO Xiangmo， HUI Fei

（School of Information Engineering， Changan University， Xian 710064， China）

Abstract： In view of the characteristics of delay and transitivity of car?following， an MOVA?based （multiple optimal velocities and accelerations） connected vehicle car?following model is proposed on the basis of the perception and cooperative interaction of connected vehicles， and the critical stability criteria of the proposed model are derived with the linear stability analysis method. Taking the disturbance imposed by the car?following process of vehicle group on the circular road as an example， the numerical simulation experiment is designed with the reference of the acceleration sensitivity coefficient [ωi] and the number [k] of multiple proceeding vehicles， and the driving stability of the vehicle group under different selected values of [ωi] and [k] is analyzed in combination with the parameters of speed and headway. The results of stability analysis shows that the proposed model has a better stability region after introducing the MOVA， and the greater the number [k] of proceeding vehicles and the greater the acceleration sensitivity coefficient [ωi]， the better the model stability. The analysis of numerical simulations indicates that， when the selected value of acceleration sensitivity coefficient [ωi] and the number [k] of proceeding vehicles are reasonable （[ωi=0.3] and [k=4]）， the fluctuation range of the vehicle group speed and headway of the proposed model is relatively small in comparison with the models of FVD， OVCM and MHOV. Therefore， the proposed model can better absorb the disturbance and enhance the stability of vehicle group.

Keywords： car?following model of connected vehicle; MOVA; critical stability determination; model stability analysis; numerical simulation analysis; disturbance absorption

0? 引? 言

交通擁堵問題對人類生活和社會運行具有重要影響，為了解決日益嚴重的交通擁堵問題，國內外相關學者圍繞車輛的跟馳建模展開大量的研究工作。車輛跟馳模型主要用來描述限制超車單行道上行駛車隊相鄰車輛間的相互作用，通常利用動力學方法研究前導車運動狀態變化所引起跟馳車的相應行為，并以數學模型表達跟馳過程中各種狀態參數的演變情況，是交通流仿真的核心基礎理論[1]。

典型的研究成果主要有：早期提出的車輛跟馳模型存在不能準確描述實際交通場景中加速度的現象[2]，為了解決這一問題，Chandler和Newell根據前后車的速度差和車間距建立基于刺激?反應的跟馳模型;Bando等圍繞Newell所提出的模型，提出了一種基于前后車車間距的最優速度模型OV（Optimal Velocity），該模型具有簡單和方便數值模擬等優點，但存在加速度異常的情形[3]。Helbing等針對OV模型未考慮前后車速度差所引起的加速度不合理問題，提出了一種廣義力（General Force，GF）模型，當跟馳車的速度大于前車時，引入前后車負速度差修正OV模型以維持合理的車間距，但是沒有考慮正速度差對跟馳車加速度的作用[4]。Jiang等考慮正負速度差對跟馳車加速度的影響，改進GF模型，提出了一種全速度差（Full Velocity Difference，FVD）模型，該模型可以較為全面地描述車輛跟馳行為，但是在維持交通流穩定性方面依然存在局限性[5]。Peng等考慮最優速度關于時間的差值項改進FVD模型，提出了一種基于駕駛員記憶的最優速度（Optimal Velocity Changes with Driving Memory，OVCM）模型，通過引入最優速度記憶項差值，使得OVCM模型在交通流穩定性方面優于FVD模型[6]。

以OVCM模型為例，在不考慮前車加速度的情形下，若前車速度小于跟馳車速度，相應地，跟馳車的加速度呈現減小趨勢;若前車處于加速階段，跟馳車需要借助前車速度信息并歷經一定的時間延遲才能捕獲車間距增大趨勢，且在延遲時間段內跟馳車的加速度仍將繼續減小。同時，在僅考慮單個前車最優速度的情形中，跟馳車只能根據單個前車進行速度調整，若考慮的前車采用先加速后減速，那么跟馳車的速度將呈現較大的波動，波動的主要原因是跟馳車所考慮的前車同樣會受到自身前車速度變化的影響，但是跟馳車不能捕獲所考慮前車的前車速度變化，從而引發跟馳車的速度出現過調。在實際駕駛環境中，如果考慮的前車速度小于跟馳車速度且處于加速狀態，則跟馳車的加速度不會立即減小，甚至在保證安全車頭距的情況下適當地給予增加;如果考慮的前車速度小于跟馳車速度且小于自身的前車速度，跟馳車的速度會在保證安全車頭距的情況下適當地給予減小，也有可能不采取減速措施。因此，考慮引入多前車行駛狀態來有效吸收車隊中多前車行駛狀態突變引發的擾動，從而提升交通流的穩定性。

在智能網聯環境中，跟馳車利用車載終端和無線通信可以獲取多輛前車的行駛狀態信息，如車頭距、速度、加速度等[7]。本文針對智能網聯車輛，結合車輛跟馳行為存在的延時性和傳遞性，引入緊鄰多前車的最優速度和加速度改進OVCM模型，提出一種基于多前車最優速度與加速度（Multiple Optimal Velocities & Accelerations，MOVA）的網聯車跟馳模型。

為了檢驗所提出模型在維持交通流穩定性方面的合理性，首先，利用線性穩定性分析計算MOVA模型的穩定性臨界條件;然后，設定不同的加速度敏感系數和多前車數，分別描述車頭距與最優速度敏感系數間的相位約束關系;最后，結合車輛速度和車頭距等多項參數，對環形道路上的車隊進行施加擾動后的數值模擬，并與OVCM等典型跟馳模型進行對比分析。

1? MOVA模型的建立

為了解決OVCM模型存在的間接解析前后車速度信息引發的延遲問題，以及更加準確地描述車輛跟馳行為特性，考慮引入緊鄰多前車的最優速度記憶項和加速度項改進OVCM模型，得到改進模型的運動方程為：

[vnt+T=Vi=1kΔxn+i-1，Δxn-1，Δvn，i=1kan+i（t）] （1）

對式（1）進行展開描述，得到式（2）：

[Vi=1kΔxn+i-1，Δxn-1，Δvn，i=1kan+i（t）? =αVΔxnt+βTΔvnt+i=1kωikTan+i-1（t）+i=1kTγiVΔxn+i-1t-VΔxn+i-1t-τ]? （2）

式中：[α]表示最優速度的敏感系數;[β]表示前后車速度差的敏感系數;[Δxnt]表示前后車車間距;[VΔxnt]表示跟馳車的最優速度函數;[T]為人為和機械因素產生的延時;[k]（[k≥1]）表示緊鄰前車的數量（含跟馳車）;[ωi]表示第[n+i-1]輛車加速度信息[an+i-1（t）]的敏感系數;[τ]表示采樣時間間隔;[γi]是第[n+i-1]輛車的最優速度記憶項[VΔxn+i-1t-VΔxn+i-1t-τ]的敏感系數。

[VΔxnt]的計算方法如式（3）所示：

[VΔxnt=Vmax2tanhΔxnt-hc+tanhhc] （3）

式中：[Vmax]為車輛的最大速度;[hc]表示車輛間的安全距離。

由于式（2）的延遲時間[T]不利于公式解析與模型仿真，且考慮到加速度對車輛控制的直接性，對式（2）進行簡化，簡化過程如式（4）～式（10）所示：

[vnt+T=vnt+Tant] （4）

將式（4）代入式（2）得：

[ant=1TVi=1kΔxn+i-1，Δxn-1，Δvn，i=1kan+i-1（t）-vnt] （5）

取[α=1T]，將式（2）代入式（5）得：

[dvntdt=αVΔxnt-vnt+? ? ? ? ? ? ? ? ? ?βΔvnt+i=1kωikTan+i-1（t）+? ? ? ? ? ? ? ? ?i=1kγiVΔxn+i-1t-Δxn+i-1t-τ] （6）

忽略變量[Δxnt-τ]泰勒展開式的非線性項計算，簡化后的[Δxnt-τ]為：

[Δxnt-τ=Δxnt-τdΔvntdt=Δxnt-τΔvnt] （7）

同理，簡化后的[VΔxnt-τ]如式（8）所示：

[VΔxnt-τ=VΔxnt-τΔvntVΔxnt]? ?（8）

將式（7），式（8）代入式（6）得到簡化的運動方程，如式（9）所示：

[dvntdt=αVΔxnt-vnt+βΔvnt+i=1kωikTan+i-1（t）+i=1kγiτVΔxn+i-1tΔvn+i-1t] （9）

2? 線性穩定性分析

為了分析判定所提出模型的穩定性，采用Lyapunov第一方法并結合線性諧波微擾法[8]分析MOVA模型的穩定性臨界條件。假設車隊穩定狀態時的車頭距為[h]，行駛速度為[V（h）]，每輛車的初始位置為[x0nt=hn+V（h）t]。如果對第[n]輛車施加擾動[ynt=eikn+zt]，則第[n]輛車經歷擾動后的位置如式（10）所示：

[xn（t）=x0n（t）+yn（t）] （10）

對式（10）求二階導數得：

[d2yn（t）dt2=dvn（t）dt] （11）

令[Δyn（t）=yn+1（t）-yn（t）]，則車頭距[h]定義如下：

[Δxn（t）=h+Δyn（t）] （12）

將式（11），式（12）代入式（9），得到與擾動相關的微分方程：

[d2yn（t）dt2=αVhΔynt-dyn（t）dt+q=1NγqτVΔxn+q-1（t）dΔyn+q-1（t）dt+βdΔyn（t）dt+q=1NωqN?d2yn+q-1（t）dt2] （13）

式中[Vh=dVΔxndΔxnΔxn=h]。

由于[ynt=eikn+zt]，令[e（ikn+zt）=eM]，將式（13）中[ynt]按傅里葉級數展開得：

[z2=αVh（eik-1）-z+βz（eik-1）+q=1NωqNeikq+q=1NγqτVhzeikq-eikq-1] （14）

將式（14）的參數[z]按[z=z1ik+z2ik2]展開，得到[z1]和[z2]的表達式：

[z1=Vh z2=12Vh+1αβz1-1-q=1NωqNe（q-1）z21+q=1Nγqτe（q-1）z1] （15）

若[z2<0]，則車隊運行狀態不穩定;反之，車隊運行狀態穩定[9]。根據式（15）中[z2]的表達式可進一步求出敏感系數[α]的取值范圍[10]，如式（16）所示：

[α>-βVh+1-q=1NωqNe（1-q）Vh2-q=1Nγqτe（1-q）VhVh] （16）

將最優速度記憶項敏感系數[γi]按照距離當前車由近到遠的次序分別定義為0.1，0.08，0.06，0.04和0.02，取前車數[k=5]，則不同[ωi]作用下車頭距[h]與最優速度敏感系數[α]的相位圖如圖1所示;取加速度敏感系數[ωi=0.5]，則不同[k]作用下車頭距[h]與最優速度敏感系數[α]的相位圖如圖2所示。

圖1和圖2中曲線均表示穩定性臨界曲線，即曲線以上部分為穩定區，以下部分為非穩定區。如圖1所示，[ωi>0]時跟馳模型的穩定區域面積大于[ωi=0]時的跟馳模型，且[ωi]的增加有利于擴大穩定區域面積;同理，根據圖2可得，[k>1]時跟馳模型的穩定區域面積大于[k=1]時的跟馳模型，且[k]的增加也能夠將穩定區域面積逐漸擴大。由此可得，引入多前車最優速度記憶項和加速度項能夠進一步維持交通流的穩定性。

3? 數值模擬與分析

利用數值模擬驗證所提出模型的有效性，將一列車隊置于環形道路，測試條件及參數設置如下[6]：環形道路總長[L]取值為400 m，車輛數[N]取值為100輛，最大速度[Vmax]取值為2[m/s]（即7.2 km/h），最優速度函數[11]為[V（Δxn（t））= 0.5Vmaxtanh（Δxn（t）-hc）+tanh（hc）]。安全車頭距[hc]為4 m，最優速度敏感系數[α]為0.41 [s-1]，前后車速度差敏感系數[β]為0.5 [s-1]，最優速度記憶項敏感系數[γi]取值均為0.2 [s-1]，采樣時間間隔[τ]定義為0.2 s，延遲時間[T]定義為1 s。數值模擬過程中，位移表達式為[sn=sn-1+vn-1τ+0.5an-1τ2]，速度表達式為[vn=vn-1+an-1τ]。

初始狀態時，定義車隊在環形道路的行駛速度為[V（LN）]，所處位置[12][xn（0）=（n-1）LN]，其中[n=1，2，…，N]。第1采樣時刻，對第100輛車施加擾動后位置為[x100（1）=LN+0.2]，觀察施加擾動后整個車隊的運行狀態。

1） 數值模擬1：描述多前車加速度項對隊列車輛速度波動幅度的影響

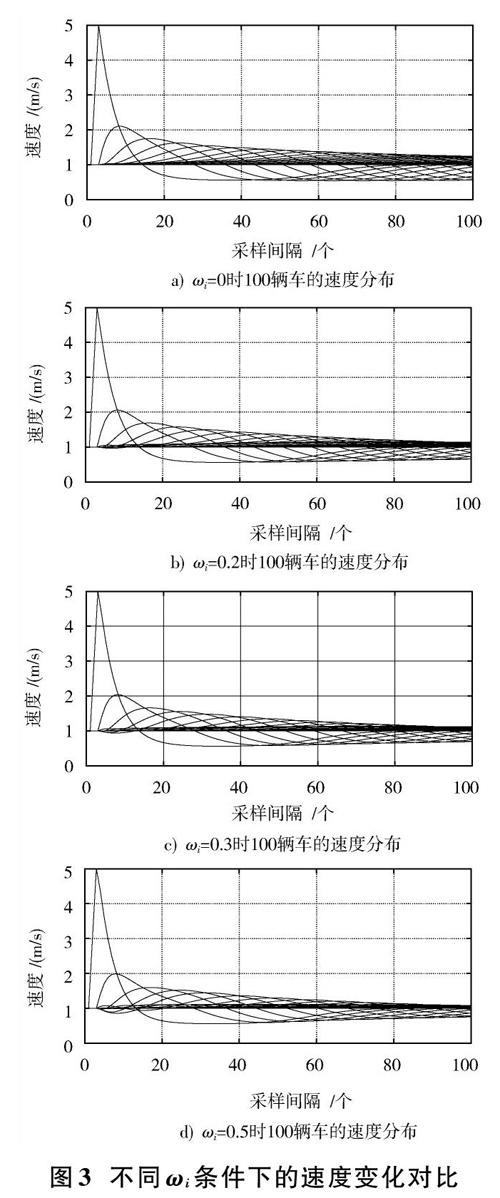
選定多前車數[k=4]，采樣間隔數為100個，車隊所有車輛的速度變化曲線如圖3所示。

分析圖3可以得出，對第100輛車加入擾動后，其速度波動幅度迅速達到最大，隨著仿真時間的推移，后續車輛的速度逐漸出現波動，且距離施加擾動車輛越遠，其速度波動幅度越小。[ωi=0]時，車隊的速度波動幅度大于[ωi≠0]時的情形，且隨著[ωi]的增大（0～0.5），車隊的速度波動幅度逐漸減小;但是，[ωi=0.3]時，在采樣時刻0～20之間的速度波動幅度小于[ωi=0.5]時的情形，故后續數值模擬過程[ωi]的取值均為0.3。

為了進一步驗證引入多前車加速度項的影響作用，設定[ωi]取值集合為[0，0.1，0.3，0.5，0.7]，定義前車數[k=5]，分別觀察100輛車在第100，200，300，400個采樣時刻的車頭距分布情況，具體分布結果如圖4所示。

由圖4可得：第100個采樣時刻，擾動主要發生在第100輛車～第80輛車;第200個采樣時刻，擾動主要發生在第90輛車～第60輛車;第400個采樣時刻，擾動主要發生在第60輛車～第20輛車。同時，第100輛車加入擾動后，4個采樣時刻的車頭距波動變化存在相似性，即[ωi=0]時的車頭距波動幅度明顯大于[ωi≠0]時的情形，且隨著[ωi]的增大車頭距波動幅度逐漸減小。

綜合圖3與圖4的測試結果，第100輛車的擾動對整個車隊的擾動影響具有延時性和傳遞性，這兩種特性的存在驗證了引入多前車加速度項的合理性和必要性，且測試結果表明，引入多前車加速度項能夠較好地穩定車速和車頭距變化幅度，有利于促進車隊的平穩運行。

2） 數值模擬2：描述多前車數[k]對隊列車輛速度波動幅度的影響

設定多前車加速度項敏感系數[ωi=0.3]（[i=1，2，…，k]），采樣間隔數為500個;對第100輛車施加擾動后，在仿真前期隊列中第100輛～第51輛車的擾動明顯大于第50輛～第1輛車，故選擇觀察第90，80，70和60輛車的速度變化，測試結果如圖5所示。

由圖5可得，不同[k]值作用下，4輛觀察車對應車頭距波動變化也存在相似性，前車數[k=4]時的車速波動幅度明顯低于[k=1]時的情形;前車數[k=6]時的車速波動幅度反而大于前車數[k=4]時的情形。由此可得，引入多前車信息（[k>1]）有利于控制隊列車速波動幅度，但是[k]的取值不宜過大，主要原因在于：距離跟馳車較遠的前車對跟馳車行駛狀態的影響逐漸減弱，[k]取值過大反而引入多余的干擾信息，從而不利于車隊穩定行駛。

3） 數值模擬3：對比OVCM等典型模型，驗證引入多前車加速度項與最優速度記憶項對車隊行駛穩定性的影響

設定多前車加速度項敏感系數[ωi=0.3]，前車數[k]取值為4。不考慮緊鄰前車加速度的影響，利用4輛前車信息對OVCM模型進行改進，可得到MHOV（Multiple Headway Optimal Velocity）模型。表1～表3描述了FVD，OVCM，MHOV和MOVA四種模型分別在第100，300和500個采樣時刻的車輛速度分布情況。參數[Vmax]，[Vave]，[Vmin]，[Rup]，[Rdn]和[Rave]分別表示最大速度、平均速度、最小速度、向上波動率、向下波動率和平均波動率。

分析表1～表3可得：FVD模型和OVCM模型隨著仿真時間的變化速度平均波動率逐漸增大，說明在前500個采樣間隔內，兩個模型的擾動沒有得到有效控制，反之，MHOV模型和MOVA模型的速度平均波動率逐漸減小。同時，MOVA模型的速度平均波動率小于MHOV模型，說明本文提出的MOVA模型在擾動吸收的控制效果和響應時間方面具備較好的優越性。

4? 結? 語

為了更好地控制車隊擾動引發的速度波動幅度，本文提出了一種基于MOVA的網聯車輛跟馳模型。線性穩定性分析表明，引入加速度敏感系數[ωi]和前車數[k]有利于增大穩定區域面積。數值模擬結果表明，隊列擾動存在延時性和傳遞性，引入多前車信息具備合理性和必要性;考慮多前車加速度項能夠有效地控制隊列速度與車頭距波動幅度;設定合理的前車數[k]，能夠使MOVA模型對速度波動幅度達到更好的控制效果;MOVA模型相比FVD，OVCM和MHOV模型，其速度平均波動率隨采樣時間的增加呈逐漸減小趨勢并達到最小值，證明該模型在促進車隊行駛穩定性方面具有更好的優越性。由于數值模擬過程和模型參數設置的局限性，下一步考慮采用實際車輛隊列數據修正MOVA模型的參數，以進一步增強MOVA模型對實際交通現象的模擬能力。

參考文獻

[1] MIKA P. Adaptive car?following model [J]. Journal of mechanical engineering， 2018， 68（3）： 281?288.

[2] 魏福祿，劉楊.經典跟馳模型的發展綜述[J].吉林建筑大學學報，2018，35（4）：19?23.

[3] AGHABAYK K， SARVI M， YOUNG W. A state?of?the?art review of car?following models with particular considerations of heavy vehicles [J]. Transport reviews， 2015， 35（1）： 82?105.

[4] ZENG Y， ZHANG N. Review and new insights of the car?following model for road vehicle traffic flow [C]// 6th International Asia Conference on Industrial Engineering and Management Innovation （IEMI）. Paris： Atlantis Press， 2016： 87?96.

[5] YU S， TANG J， XIN Q. Relative velocity difference model for the car?following theory [J]. Nonlinear dynamics， 2018， 91（3）： 1415?1428.

[6] PENG G， LU W， HE H， et al. Nonlinear analysis of a new car?following model accounting for the optimal velocity changes with memory [J]. Communications in nonlinear science & numerical simulation， 2016， 40：197?205.

[7] 趙祥模，惠飛，史昕，等.泛在交通信息服務系統的概念、架構與關鍵技術[J].交通運輸工程學報，2014（4）：105?115.

[8] YU S W， SHI Z K. An improved car?following model consi?dering relative velocity fluctuation [J]. Communications in nonli?near science & numerical simulation， 2016， 36： 319?326.

[9] NGODUY D. Linear stability of a generalized multi?anticipative car following model with time delays [J]. Communications in nonlinear science and numerical simulation， 2015， 22（1/3）： 420?426.

[10] 秦嚴嚴，王昊，冉斌.考慮多前車反饋的智能網聯車輛跟馳模型[J].交通運輸系統工程與信息，2018，18（3）：48?54.

[11] 李騰龍.網聯車環境下跟馳行為建模及交通流穩定性分析[D].西安：長安大學，2017.

[12] ZHU W X， ZHANG L D. A new car?following model for autonomous vehicles flow with mean expected velocity field [J]. Physica A： statistical mechanics and its applications， 2018， 492： 2154?2165.