平面多自由度機械手定位誤差的反演校正量計算

湯受鵬

（山東商務職業學院機電工程系，山東煙臺264670）

0 引 言

機器人的種類繁多，應用非常廣泛，比如軍用、民用和工業用機器人等[1-2]，其中工業用機器人機械手的研究是人們比較關注的領域。機器人機械手有空間結構和平面結構兩種形式，其運動分析和動力學分析基本上是類似的，都是要通過建立基本坐標系和局部隨動坐標系及其坐標變換（雅可比矩陣）取得控制空間參量和操作空間參量之間的函數關系方程（組），但這些方程大多為非線性的代數方程或微分方程，其對應的正反演解析求解非常困難。徐建強[3]對并聯機構運動分析和動力分析常用的雅可比矩陣求解、直接求導法、牛頓迭代法、影響系數法、虛設機構法和數值搜索法等數學方法做了介紹，這些方法在末端執行器的速度分析和加速度分析及執行力的正反演求解中都有應用；夾具設計及其誤差分析理論在機器人的分析中也是可以借鑒的，吳玉光等[4]將工件和夾具系統進行了機構模型化，對夾具定位誤差提出了機構學建模方法。由于機器人的控制空間參數和操作空間參數之間的關系大多為強非線性的，一般解析求解很困難，近些年來人們提出的差分進化算法[5]、混沌相乘法[6]、多種群遺傳算法[7]、復合形差分進化算法[8]、追隨軌跡算法[9]等理論[10-12]都在一定程度上了給出了具體問題的（數值）解。龔星如[13]針對TX90XL工業機器人的運動學建模、標定方法及標定的可行性做了研究；王雪巍[14]對埃夫特工業機器人ER7L的幾何誤差問題采用預給運動學參數誤差方法探討了長度誤差、角度誤差及其他一些微小誤差對末端定位精度的敏感性問題；廖偉強等[15]對游藝人形機器人的關節結構及運動采用人體工學原理和有限元方法進行了研究，給出了關節位置和速度的求解方法，分析了機器人運動的平穩性等問題；胡俊峰等[16]針對一種新的兩自由度柔性并聯機械手采用假設模態法和拉格朗日乘子法給出了系統的動力學模型和運動控制模型，并利用坐標分塊法對該模型進行了分析求解。理論上機器人在工作過程中按照預先設定的程序是可以準確到達目標工作點的，但實際上是不可能做到的，原因是各種形式的誤差總是存在的，這就需要機器人能進行位置傳感反饋調整，進行二次補償定位，這種反饋補償定位的數學模型原則上一般都是非線性的，但因為目前的設計水平和加工技術等先進設計理念，總是能夠做到定位誤差是比較小的程度，這個事實使得問題變得簡單了，那就是原本非線性反演問題將可以轉化為一個比較簡單的線性分析模型，這種線性模型一般來說隨著機械手的自由度的增加而成為欠定的，即通過該模型的求解將得到無數組反饋調整參數方案，這為下一步的優化尋優帶來了方便，本文基于這樣的考慮，針對一個平面n自由度機械手執行端的定位誤差反演關節參數問題提出了一種線性分析模型，通過建立適當的優化目標函數找到最佳反演關節參數調整解，其中采用了共軛梯度法對目標函數進行了優化尋優，從參考文獻看，目前未見有類似文獻發表，本文的分析方法和結論對于平面機械手和空間機械手的微調反演問題研究都具有一定的參考價值。

1 問題模型和理論分析

圖1所示是一根平面多自由度機械手，它由n根連桿通過n－2個活動平面鉸鏈連接而成，并通過A1處的一個平面固定鉸鏈與基座相連，這是一個開環連接的平面結構，是機器人操作機構上經常采用的結構形式之一。建立圖示平面直角坐標系xA1y（固定坐標系，也稱基本坐標系）

上述結構中，關節點Aj（j=1,2,...,n）處一般安裝有驅動動力 源，An+1處 安裝操作手（機器人執行端），為了下文討論方便起見，不再考慮此處的運動自由度（比如說腕部旋轉自由度）。假設點An+1的坐標為（xn+1,yn+1），連桿A1A2與基本坐標系的水平軸（x軸）之間的夾角為θ1，連桿A2A3與連桿A1A2之間的夾角為θ2，依此類推，連桿AnAn＋1與連桿An－1An之間的夾角為θn，并規定凡逆時針轉向為正，反之為負。連桿長度分別為Lj（j=1,2,...,n）。

根據圖1的幾何關系，在某一工序中，機械手位于圖示工作位置，即其對應的定位關節參數分別為θj（j=1,2,...,n），容易列出（xn+1,yn+1）與θj（j=1,2,...,n）之間滿足的方程組：

假設由于各種原因（比如連桿變形和/或尺寸誤差、關節連接處的配合間隙等），該機械手的操作端An+1離真正的目標點存在水平方向的誤差ε，豎直方向上的誤差η。為此，對式（1）兩邊同時微分得：

若令dxn+1=ε,dyn+1=η,dθj=δj，則上式可改寫為：

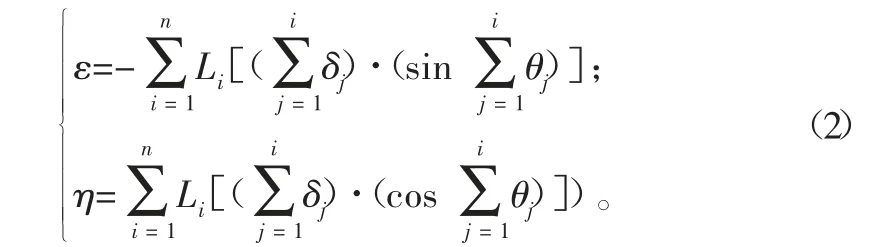
式中，δk（k=1,...,n）分別是角度（關節參數）θk（k=1,...,n）的微調量。

式（2）就是在知道ε,η的前提下確定δk（k=1,...,n）的問題，這是一個欠定反演問題，一般來說理論上它具有無窮多組解。此外，根據實際問題的具體情況，比如能量消耗最小或調整效率最高或調整用時最短等要求，總是可以給出一個選定解的評判準則，在優化問題上就是目標函數的構造問題，在這里不失一般性，我們假定該目標函數是解的2-范數，即有如下優化模型：

式中：δ=［δ1,...,δn］T，T為轉置。

通過求解式（3），就可以找到取得最小2-范數的反饋誤差校正量δ=［δ1,...,δn］T。

對于式（2），選定［δ3,...,δn］T作為自由變量，確定變量δ1、δ2。

以變量（δ3,...,δn）為自由變量，通過式（2）確定變量（δ1,δ2）的方程組為：

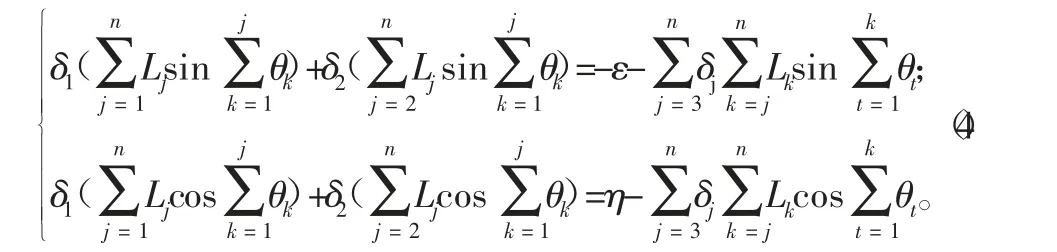
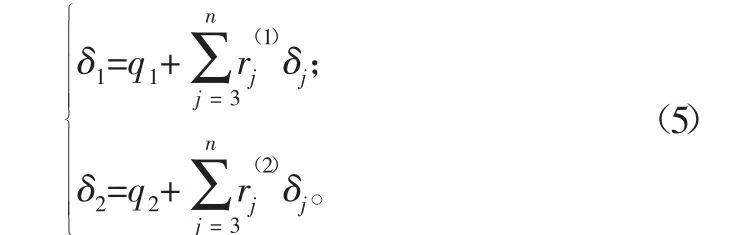
式中：

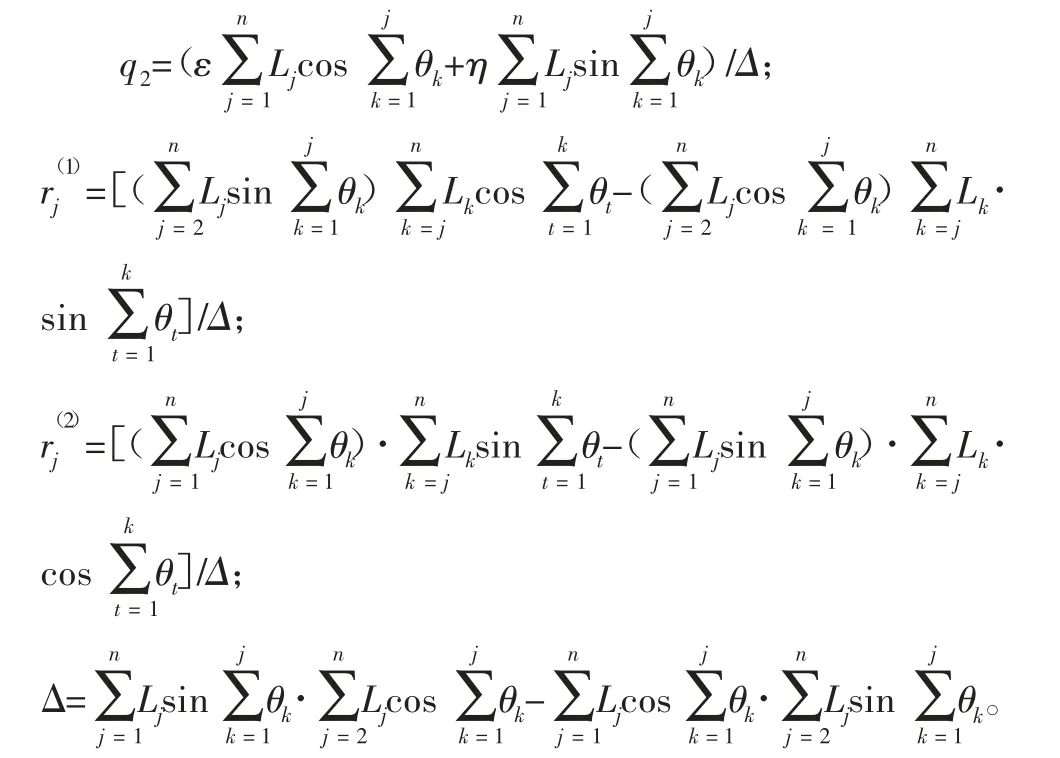
問題的目標函數可進一步寫為

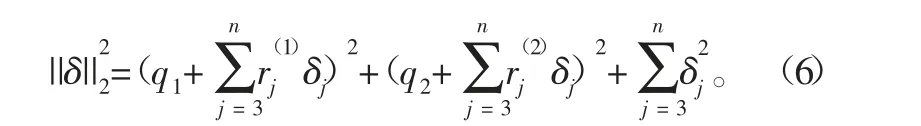
顯然該目標函數是關于變量δj（j=3,...,n）的二次函數，具有唯一極小點，該極小點滿足如下條件：

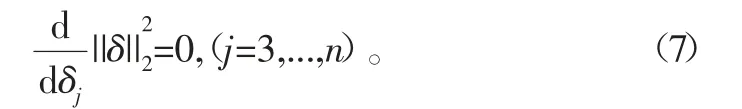
即

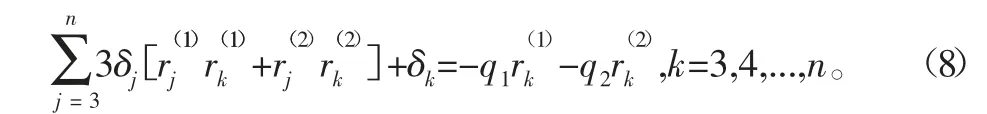
簡寫之為

式中：x=［δ3,δ4,...,δn］T；

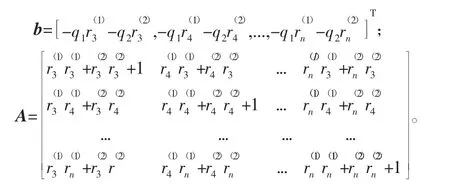
求解線性方程組的方法有很多，考慮到機器人運動定位參數誤差反演計算的病態性現象的廣泛性，本文采用具有一定抗病態性的共軛梯度法求解上述方程組。

為此，為保證方程組系數矩陣的正定性，將式（9）做如下處理：

容易驗證，矩陣B=ATA是對稱正定的，且方程組ATAx=ATb與Ax=b有共同解。

具體共軛梯度法求解的迭代過程設計如下

1）給定計算精度γ和初始迭代點x0，計算其負梯度g0=－▽f（x0），并令第一個共軛向量S0=g0。

2 算例結果與分析（swp107）

驗證本文算例的已知參數給出為L1=0.2 m，L2=0.3 m，L3=0.4 m，L4=0.5 m，L5=0.5 m，L6=0.8 m；θ1=π/12，θ2=π/10，θ3=π/8，θ4=π/10，θ5=π/9，θ6=π/6；ε=0.006 m，η=0.005 m，計算結果為δ1=－0.0015 m，δ2=－0.0018 m，δ3=－0.0024 m，δ4=－0.0014 m，δ5=－0.0001 m，δ6=－0.0014 m。當ε=－0.004 m，η=0.008 m時，計算結果為δ1=－7.1615×10-4m，δ2=－6.7885×10-4m，δ3=0.001 1 m，δ4=－0.0 008 m，δ5=0.000 m，δ6=－0.0002 m，這些解就是反饋給機械手進行關節微調的量。上述兩種情況的尋優都用了四次迭代，迭代速度是非常快的。

從上述計算結果看，在機械手離真實位置存在（位置）誤差時，利用本文方法可以快速計算出機械手各個關節處需要微調的參數值，可為反饋控制關節驅動器的驅動方向和調節量提供參考。當然，當選擇解的評判標準發生變化時，僅僅需要改變優化目標函數的形式，然后采用合適的線性近似分析即可。

3 結 論

本文對平面n自由度機械手的操作位置誤差反饋控制參數反演提出了一種線性分析方法，該法可給出問題的解析解，并能夠推廣用于機械手的三維真實空間內的誤差反演調整量的計算。