超材料混凝土的帶隙特征及對沖擊波的衰減效應*

張 恩，路國運，楊會偉，曹瑞東，陳鵬程

（1. 太原理工大學土木工程學院，山西 太原 030024；

2. 太原理工大學材料強度與結構沖擊山西省重點實驗室，山西 太原 030024；3. 山西大學土木工程系，山西 太原 030013）

近年來關于人造具有特殊功能材料的設計和制造成為研究熱點，超材料（metamaterials）是人造復合材料，具有天然材料不具備的非凡的物理性質。這些特性源于其特殊設計的微觀結構，而不是化學成分。超材料的出現代表著一種嶄新的材料設計理念，即人類可以在利用現有材料的基礎上，按照自己的意志逆向設計微結構來獲得新材料。超材料的研究主要集中在電磁超材料[1-2]、熱學超材料[3-4]、光學超材料[5-6]和聲學超材料[7-13]等領域。

Liu 等[10-13]提出了局域共振聲子晶體，使用橡膠包裹鉛球構成局域共振單元。在環氧樹脂基體中周期性地排列上述局域共振單元，可以構成人工周期材料。上述周期材料突破Bragg 機理的限制，使用彈性波的局域共振效應實現了在亞波長頻段對低頻彈性波的衰減，為聲學超材料的研究開拓了新思路。Yang 等[14-15]使用局域共振的思想設計了薄膜型主動聲學超材料，能夠對50～1 000 Hz 的低頻聲波進行阻隔，并進一步探索出有效拓寬局域共振聲學超材料帶隙的方法。吳健等[16]、張印等[17]使用局域共振的思想設計了梁板類聲學超材料，并對其帶隙計算方法進行改進和完善，最后把該類聲學超材料應用于聲隱身和減振降噪等領域。Br?lé等[18]把局域共振的思想引入到防震工程中，其通過在黏土中打出中心間距為1.73 m、深度為5 m、直徑為0.32 m 的自穩定孔，實現了對頻率為50 Hz 的彈性波的阻斷。

本文中，借鑒超材料的研究思路，使用局域共振骨料代替混凝土中的普通骨料，設計一種具有沖擊波衰減效應的超材料混凝土。首先，基于結構動力學計算了超材料混凝土的有效質量，并進一步建立超材料混凝土帶隙起始頻率、截止頻率的理論模型，討論涂層彈性模量、芯柱密度、基體密度、骨料體積占比和芯柱邊長與軟涂層厚度比等因素對超材料混凝土帶隙起始頻率、截止頻率及帶隙寬度的影響；其次，采用數值模擬的方法，對比超材料混凝土和普通混凝土對沖擊波的衰減效應。以期研究結果可為超材料混凝土的設計及應用提供理論支持。

1 超材料混凝土設計

本文中提出的超材料混凝土（metaconcrete）如圖1 所示，由局域共振型骨料和砂漿兩部分組成。其中局域共振型骨料由高密度柱體周圍包覆軟涂層形成，把該骨料均勻地排列在砂漿中，形成超材料混凝土。最初，局域共振型結構多被設計成球形和圓柱形結構[10-13]，但是在實際使用中，球形和圓柱形結構存在制作難度大、加工復雜等問題，為此設計了長方體形結構，其具有以下優點：芯柱制作過程簡單；軟涂層的工藝更易實現；便于工程應用。當沖擊波從一端向另外一端傳播時，由于軟涂層的存在，芯柱和砂漿可以產生相對運動，起到衰減沖擊波的目的[19]。

圖1 本文中提出的超材料混凝土Fig. 1 Metaconcrete designed in this paper

2 有效質量及帶隙特征

2.1 有效質量理論模型

圖2(a)為超材料混凝土單胞，其中砂漿基體質量為m1，芯柱質量為m2，軟涂層等效為剛度為k2的彈簧，砂漿和芯柱的位移分別為u1和u2。超材料混凝土可視為圖2(b)所示的一維晶格系統。為了計算超材料混凝土的有效質量，又可以把圖2(b)假設為如2(c)所示的由剛度為k1(k1→∞)的外部彈簧連接的一維超材料混凝土晶格系統。

對于圖2(a) 所示的超材料混凝土單胞，假設涂層為均勻彈性材料，在計算軟涂層的等效剛度k2時，只考慮左右兩側軟涂層的拉伸和壓縮作用，忽略前后兩側軟涂層的剪切作用，等效剛度k2可以簡化為：

式中：E 為涂層的彈性模量，b 為芯柱的邊長，l 為芯柱的高度，t 為軟涂層厚度。

對于圖2(c) 所示的一維晶格系統，根據動力學平衡方程，可以給出第j 個單胞的運動方程：

圖2 超材料混凝土單胞及一維晶格系統Fig. 2 A unit cell and one-dimensional lattice systems for metaconcrete

考慮周期系統的穩態簡諧振動，可設位移解[20]為：

式中：A 為波幅，q 為波數，L 為單胞的邊長，ω 為激振頻率。

從而：

從而式（2）和式（3）可以簡化為：

再次使用下列恒等式：

式（7）和式（8）可以簡化為：

為了得到系統的色散關系，可以把式（11）和式（12）看成求解矩陣特征值的問題，可以簡化為如下形式：

式中：Kr和Mr分別為系統的剛度矩陣和質量矩陣，ω 為頻率，u 為系統中自由度的位移矢量。從而，系統的運動方程可以寫成下列形式：

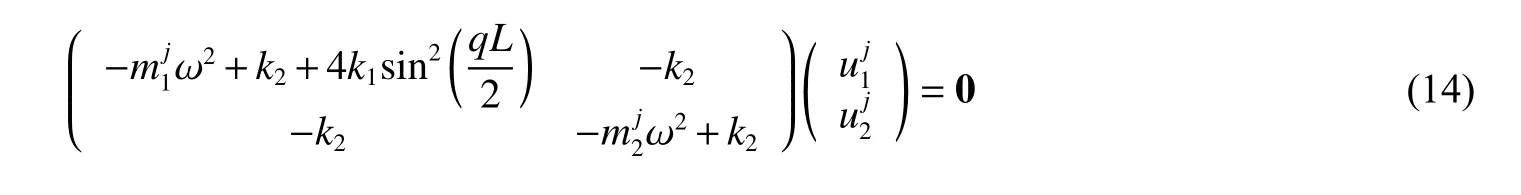
Kr-ω2Mr=0

當且僅當 時，此特征值問題具有非零解。從而：

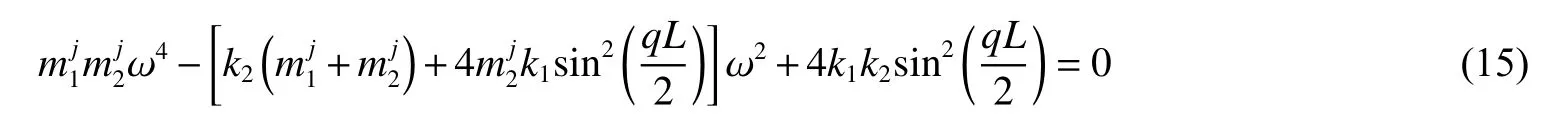
結合式（9）～（10）和（15），可以得到：

對于圖2（d）中的一維單原子晶格系統，其等效質量meff[20-21]可以表示為:

結合公式（16）和（17），可以得到無量綱的meff表達式：

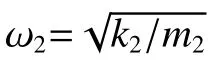
根據式（18），當θ=1，可以給出有效質量與激振頻率的關系圖，如圖3 所示。

如圖3 所示，當激振頻率接近由彈簧-芯柱組成的內部系統的自振頻率時，有效質量曲線變化特別大并且復雜，當ω＞ω2時，達到負值。圖中A、B 兩點之間的區域，有效質量達到負值，波在該頻率范圍內會得到衰減，形成帶隙[16-17]。因此，有效質量是激振頻率的函數，正是接近內部系統自振頻率的行為導致材料整體性能的變化，從而能夠形成一種具有消波能力的新穎材料。

2.2 帶隙特征分析

圖3 有效質量與激振頻率的關系Fig. 3 Relationship between effective mass and excitation frequency

結構的帶隙是指不能通過該結構的波的頻率范圍，其特征主要包含帶隙起始頻率（band gap start frequency）、帶隙截止頻率（band gap cutoff frequency）和帶隙寬度（band gap width）。對比圖3，其中A 點對應帶隙起始頻率，其主要由局域共振骨料的平動振動決定；B 點對應帶隙截止頻率，根據式（18），求出該點對應的頻率，表明該共振模式下，芯柱與基體在涂層的作用下，形成反相位，達到動態平衡。

采用圖4 所示模型來進一步描述以上兩種共振模式。

圖4 中，M1為單個局域共振型骨料中芯柱的等效質量，M2為單個周期內砂漿的等效質量，彈簧k 為骨料涂層的等效剛度。在帶隙起始頻率處，芯柱M1在彈簧k 的作用下發生共振；而在帶隙截止頻率處，芯柱M1和砂漿M2在彈簧k 的連接下，以相對振動的方式發生共振，彈簧上黑點所示位置保持相對靜止。

圖4 帶隙起始頻率及截止頻率的簡化模型[22]Fig. 4 Simplified models for band gap start and cutoff frequencies[22]

對式（18）進行轉換，可以得到帶隙起始頻率f1和帶隙截止頻率f2的函數表達式：

由此可知：能夠影響局域共振骨料等效質量或等效剛度的材料和結構參數，均對局域共振帶隙的起始頻率產生影響；同時，能夠影響局域共振骨料等效質量、等效剛度或基體等效質量的材料和結構參數，均對局域共振帶隙的截止頻率產生影響。

3 帶隙特征影響因素分析

為了更加深入探究局域共振型超材料混凝土的帶隙特征，本文討論不同參數對超材料混凝土帶隙特征的影響，以加深對此共振結構消波機理的認識，用于指導超材料混凝土的結構設計及材料選擇。

3.1 涂層彈性模量對帶隙的影響

由式（19）和（20）可知，涂層彈性模量會對等效剛度產生較大的影響。為研究不同涂層材料對帶隙特征的影響，在保證其他參數不變的情況下，僅改變涂層彈性模量。現選取單胞的邊長L=20 cm，芯柱的邊長b=10 cm，軟涂層厚度t=1 cm，芯柱材料為鉛（Pb，密度為11.6 Mg/m3），基體材料為砂漿（密度為2 Mg/m3）。涂層材料的相關參數參考文獻[23]。

圖5 給出了涂層彈性模量對帶隙特征的影響。從圖中可以看出，隨著涂層彈性模量的增大，帶隙起始頻率、截止頻率及寬度均增大。根據前文所述，帶隙起始頻率對應骨料自振，帶隙截止頻率對應骨料和基體相對某平衡位置產生共振，涂層起到彈簧的作用，涂層彈性模量越大，等效剛度越大，頻率越高。當涂層的彈性模量為0.2 MPa 時，其對應的帶隙起始頻率、截止頻率和寬度分別為20.91、36.69 和15.78 Hz；當涂層的彈性模量為1.0 MPa時，其對應的帶隙起始頻率、截止頻率和寬度分別為46.75、82.04 和35.29 Hz。可見，柔性的涂層能夠形成低頻帶隙，但是帶隙寬度較窄，而高彈性模量涂層能夠形成較寬的帶隙，但帶隙起始頻率較高。因此，可以根據所需衰減的波的頻率進行涂層材料的選擇。對于用作防止爆炸等高頻載荷的材料，超材料混凝土必須在高頻下展現共振行為，應選擇高彈性模量的涂層材料。對于用作防止地震等低頻荷載的材料，超材料混凝土必須在低頻下展現共振行為，應選擇低彈性模量的涂層材料。

3.2 芯柱密度對帶隙的影響

由式（19）和（20）可知，芯柱密度會對等效質量M1產生較大影響，因此，需要進一步研究芯柱密度對帶隙特征的影響。采用3.1 節的幾何尺寸，涂層材料選擇silicone（彈性模量為1 MPa），芯柱材料選擇鋁、鋼、銅和鉛，其對應的密度分別為2.7、7.9、8.89 和11.6 Mg/m3[22]。

圖6 給出了帶隙特征隨芯柱密度變化的曲線。從圖6 可以看出，隨著芯柱密度的增大，帶隙起始頻率和截止頻率均降低且帶隙起始頻率降低的速度較快，從而帶隙寬度增大。當芯柱材料為Al 時，帶隙起始頻率、截止頻率和寬度分別為96.91、118.05 和21.14 Hz；當芯柱材料為Pb 時，帶隙起始頻率、截止頻率和寬度分別為46.75、82.04 和35.29 Hz。可見，高密度芯柱材料能夠形成低頻帶隙，且帶隙寬度較大，而低密度芯柱材料更容易形成高頻帶隙，且帶隙寬度較低。因此，若需要得到低頻、寬帶隙等特征，應選擇密度較高的芯柱材料。

3.3 基體密度對帶隙的影響

由式（19）和（20）可知，基體密度會對等效質量M2產生影響，因此，需要進一步研究基體密度對帶隙特征的影響。采用3.1 節的幾何尺寸，涂層材料選擇silicone（彈性模量為1 MPa），芯柱材料選擇Pb（密度為11.6 Mg/m3）。

圖7 給出了帶隙特征隨基體密度變化的曲線。從圖7 可以看出，隨著基體密度的增大，帶隙起始頻率保持不變，帶隙截止頻率和寬度持續減小。主要原因是：帶隙起始頻率對應芯柱的自振，其主要由芯柱等效質量及軟涂層等效剛度決定，基體密度的變化不會影響芯柱的等效質量，從而帶隙起始頻率不會產生變化；帶隙截止頻率，對應芯柱與基體動態平衡，其主要由芯柱等效質量、涂層等效剛度和基體等效質量決定，基體密度的增大會導致基體等效質量增加，從而使得帶隙截止頻率持續減小，又因為帶隙起始頻率保持不變，最終帶隙寬度也會持續減小。因此，若需要得到低頻、寬帶隙等特征，應選擇密度較低的基體材料。

圖6 芯柱密度對帶隙特征的影響Fig. 6 Effects of core column density on band gap

圖7 基體密度對帶隙特征的影響Fig. 7 Effects of matrix density on band gap

3.4 骨料體積占比對帶隙的影響

為了解骨料體積占比對帶隙特征的影響，對于典型的正方形單元，定義骨料體積占比β=R2/a2。其中，R=b+2t，b 為芯柱邊長，t 為涂層厚度，a 為周期常數。在討論骨料體積占比對帶隙特征的影響時，需要保持參數γ（γ 為芯柱邊長與軟涂層厚度的比值，γ=b/t）不變。涂層材料選擇silicone（彈性模量為1 MPa），芯柱材料選擇Pb（密度為11.6 Mg/m3），基體密度為2 Mg/m3，L=2 cm，γ=10。

圖8 給出了帶隙特征與骨料體積占比（β）的關系。從圖8 可以看出，帶隙起始頻率隨著β 的增大而持續降低，且在β 從0.1 到0.4 時，降低速度較快，之后降低速度減緩；帶隙截止頻率隨β 的增大呈現先降低再升高的趨勢，其中β 從0.1 到0.4 時，帶隙截止頻率持續降低，之后，帶隙截止頻率隨β 的增大而升高，且在β 從0.1 到0.4 時，帶隙起始頻率的降低速度大于帶隙截止頻率的降低速度，最終帶隙寬度隨著β 的增大而持續增大。因此，可以通過增大骨料體積占比的方式來實現擴寬帶隙的目的。

3.5 芯柱邊長與軟涂層厚度比對帶隙的影響

圖8 γ=10 時，骨料體積占比對帶隙特征的影響Fig. 8 Effect of volume fraction of aggregate on band gap when γ=10

為了研究參數γ 對帶隙特征的影響，需要保證骨料體積占比β 不變。涂層材料選擇silicone（彈性模量為1 MPa），芯柱材料選擇Pb（密度為11.6 Mg/m3），基體密度為2 Mg/m3，L=2 cm，骨料體積占比β=0.36。

圖9 給出了骨料體積占比為36%時，參數γ 對帶隙特征的影響。從圖9 可以看出，帶隙起始頻率及截止頻率均隨著γ 的增大呈現出先減小再增大的變化趨勢，而帶隙寬度隨著γ 的增大而持續增大。其中，帶隙起始頻率在γ=2 左右取得極小值；帶隙截止頻率在γ=1 左右取得極小值。因此，若需要得到寬帶隙特征，可以通過增大參數γ 來實現。

圖9 當β=0.36 時，γ 對帶隙特征的影響Fig. 9 Effect of γ on band gap when β=0.36

4 超材料混凝土對沖擊波的衰減效應

4.1 有限元模型

為了說明超材料混凝土對沖擊波的衰減作用，使用LS-DYNA 建立如圖10（a）所示的超材料混凝土有限元模型，其長度為100 mm，寬度為60 mm，厚度為20 mm。整個模型包含60 000 個單元和67 771 個節點，砂漿、軟涂層和芯柱均使用八節點的solid 單元。為了消除邊界效應的影響，在上下兩個側面設置對稱性邊界條件；為保證混凝土板不發生位移，在前后兩個側面設置固定邊界條件[19]。在模型左側施加如圖11 所示沖擊波。在保證計算精度的情況下，對模型進行簡化。混凝土基體、涂層和芯柱均采用線彈性材料模型[23]，3 種材料之間采用共節點的方式進行連接。同時，為了對比超材料混凝土的優越性能，建立了如圖10（b）所示的同樣條件下的普通混凝土有限元模型。

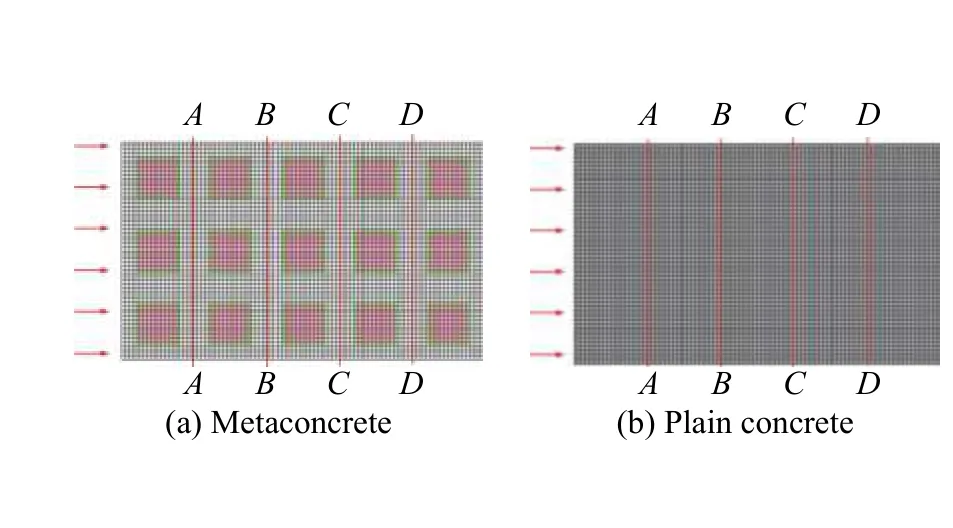
圖10 有限元模型俯視圖Fig. 10 The top views of finite element models

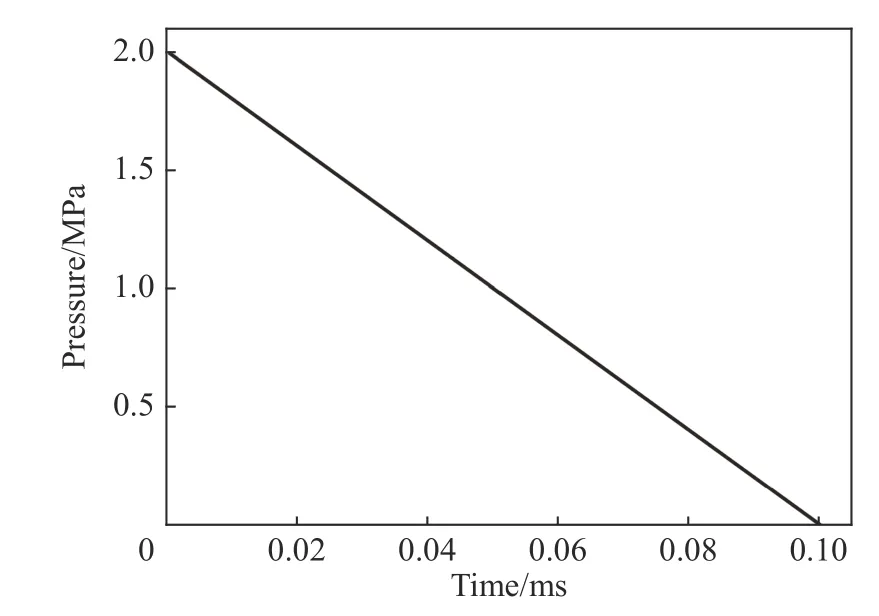
圖11 沖擊波壓力-時間曲線Fig. 11 Pressure-time curve of shock wave

4.2 超材料混凝土對沖擊波的衰減

如圖10 所示，對于超材料混凝土和普通混凝土，均在距離沖擊端20 mm（截面A-A）、40 mm（B-B 截面）、60 mm（截面C-C）和80 mm（截面D-D）處依次選取4 個截面，得到各截面的平均應力時程曲線，如圖12 所示。從圖12 可以看出，對于超材料混凝土和普通混凝土，各截面的平均應力均隨著時間的增加而降低，但超材料混凝土中的平均應力降低較快。以1.0 ms 左右為例，超材料混凝土中各截面的平均應力在-0.2～0.2 MPa之間，而普通混凝土中各截面的應力在-0.4～0.4 MPa 之間。因此，與普通混凝土相比，超材料混凝土對沖擊波具有更好的衰減作用。

圖12 各截面平均應力時程曲線Fig. 12 Average stress-time curve at each section

5 結 論

借鑒超材料的研究思路，在混凝土中引入諧振骨料，設計出具有消波特性的超材料混凝土，并對其帶隙特征和沖擊波衰減效應進行研究，得到以下結論：

（1）低彈性模量的涂層能夠形成低頻帶隙，但是帶隙寬度較窄，而高彈性模量涂層能夠形成較寬的帶隙，但帶隙起始頻率較高。因此，應根據所需衰減的波的頻率進行涂層材料的選擇。

（2）高密度芯柱材料能夠形成低頻帶隙，且帶隙寬度較大，而低密度芯柱材料更容易形成高頻帶隙，且帶隙寬度較小。因此，若需要得到低頻、寬帶隙等特征，可以選擇密度較高的芯柱材料。

（3）基體密度的變化對帶隙起始頻率沒有影響，但基體密度的升高使帶隙截止頻率降低和帶隙寬度減小。因此，選擇低密度的基體材料可以擴寬帶隙。

（4）通過增大骨料體積占比和芯柱邊長與軟涂層厚度比可以實現擴寬帶隙的目的。

（5）與普通混凝土相比，超材料混凝土對沖擊波具有更好的衰減作用。