一種低能耗與高精確度的WSN數據融合算法
宋 蕾,任秀麗
(遼寧大學 信息學院,沈陽 110036)
0 概述
無線傳感網中數據融合[1]是指將同一目標的多個觀測數據相互融合,以減少數據冗余并提高系統可靠性[2],進而延長網絡生命周期。傳感器節點在數據采集、傳輸與統計過程中,隨著網絡時延增加、通信量增多和節點生命周期縮短等問題[3],致使數據精確度下降,且節點能耗隨之增加。
針對節點能耗和數據精確度問題,文獻[4]提出低能耗的E-CPDA算法,在提高數據精確度的同時增加了簇結構動態變化的能耗。文獻[5]提出面向車組網的MGDAA算法,通過綜合數據的冗余和互補信息來提高融合精確度,但會增加節點能耗。文獻[6]提出基于車輛檢測器數據壓縮重構和交通流特征的Megrez算法,提高了數據精確度,但也增加了節點能耗。針對上述算法存在的問題,本文提出一種基于博弈論的數據融合算法(Data Fusion Algorithm Based on Game Theory,DFABGT)。該算法分為基于博弈論[7]的節點選取和基于貝葉斯理論[8]的數據融合兩部分,簇內節點通過收益和能耗確定效益函數選取低能耗節點,再將效益函數的最大值作為權重代入置信距離得到可靠數據。
1 網絡模型
在無線傳感網中,n個節點構成m個簇結構。簇頭收集簇內節點傳輸的數據,Sink節點融合數據,以保證全局最優[9]。1)傳感器節點同構且位置固定,感知半徑、通信能力和初始能量相等,每個節點具有唯一ID,且周期性地向簇頭傳輸數據;2)節點非均勻分布,簇頭能感知簇內節點的位置與剩余能量,簇內節點能感知自身剩余能量;3)不論剩余能量是否有限,能耗控制均需在節點承受的能量范圍內;4)節點自感知且主動收集數據,Sink節點沒有能量限制。網絡模型[10]如圖1所示。
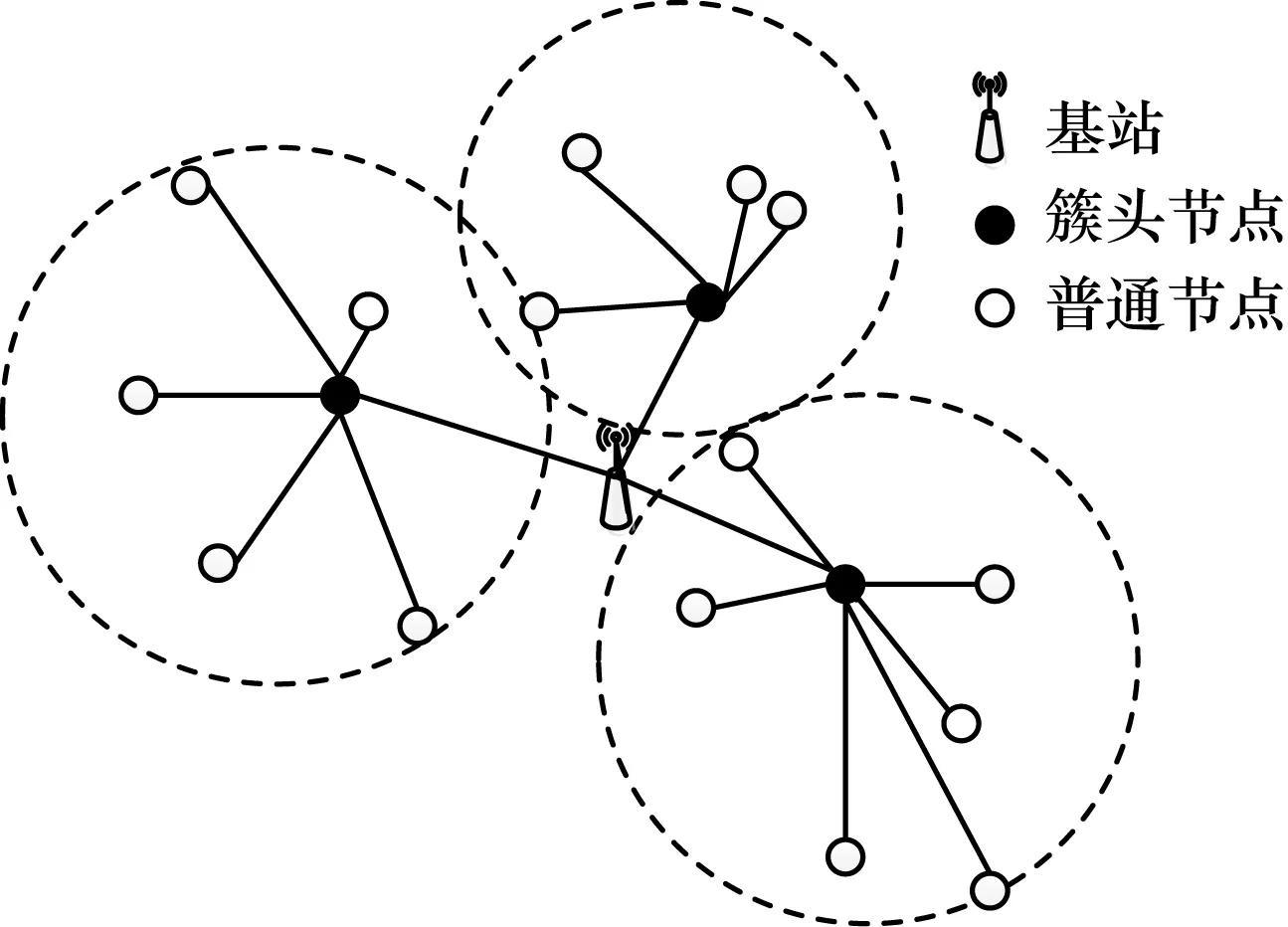
圖1 網絡模型
2 DFABGT算法
DFABGT算法分為基于博弈論的節點選取和基于貝葉斯理論的數據融合兩部分。基于博弈論的節點選取以降低能耗為目標,簇內節點通過效益函數最大值選取最佳策略。基于貝葉斯理論的數據融合以提高數據精確度為目標,簇頭通過置信距離選取有效數據傳輸給Sink節點,并采用貝葉斯融合數據。
2.1 基于博弈論的節點選取
簇內節點通過收益和能耗相互博弈選取最佳策略得到低能耗節點。博弈論[11]的基本要素為參與者、策略和效益函數。參與者指需要決策的個體,即簇內節點。策略指具體規則,令節點具有選擇善意融合(Good Fusion,GF)、惡意融合(Bad Fusion,BF)與不融合(Not Fusion,NF)的能力,記為S={GF,BF,NF}。效益函數指行動函數,以判斷不同策略的期望值。效益函數由收益和能耗構成,具有如下要素:
要素1收益(α)用于判斷節點是否參與數據融合處理,其中,αi=1表示第i個節點參與融合處理,αi=0為不參與融合處理,收益集合記為{α1,α2,…,αn}。
要素2善意融合能耗WG表示節點融合數據包的能耗。
要素3惡意融合能耗WB表示由于鏈路信道、節點或數據包遭受網絡攻擊導致融合呈現惡意結果,其能耗值為融合數據包的能耗與網絡攻擊的能耗(WA)。
要素4不融合能耗WN表示任意兩個節點中若有一個節點不參與融合,則另一個節點有融合能耗但沒有收益;若兩個節點均不參與融合,則節點均沒有收益或能耗。
不同策略組合形成的效益值構成博弈策略(如表1所示),說明如下:
1)假設節點i與節點j均選擇融合策略時,節點i與節點j均有收益(αi=αj=1)且為對方付出相應的融合能耗;當節點i選擇融合策略、節點j選擇不融合策略時,節點i與節點j均沒有收益(αi=αj=0),節點j付出不融合能耗但節點i付出相應的融合能耗。
2)假設節點i選擇不融合策略、節點j選擇融合策略時,節點i與節點j均沒有收益(αi=αj=0),節點j付出不融合能耗但節點i付出相應的融合能耗;當節點i與節點j選擇不融合策略時,節點i與節點j均沒有收益(αi=αj=0)或能耗。
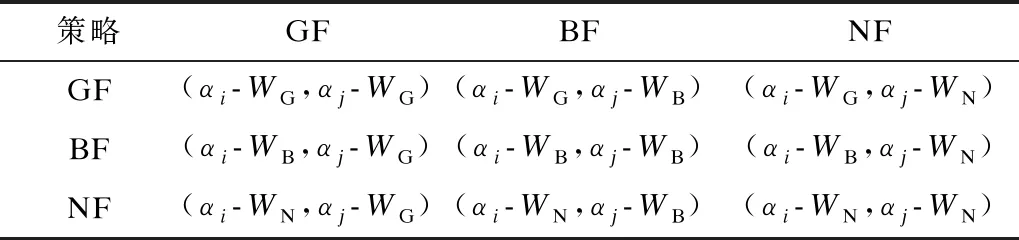
表1 博弈策略
參與融合的任意兩個節點中一個節點選擇善意融合、惡意融合與不融合的概率為β1、β2、β3,且β1+β2+β3=1表示全部的決策內容;另一個節點選擇善意融合、惡意融合與不融合的效益函數記為p(GF)、p(BF)、p(NF),計算公式如下:
p(GF)=β1×(1-WG)+β2×(1-WG)+β3×WG
(1)
p(BF)=β1×(1-WB)+β2×(1-WB)+β3×WB
(2)
p(NF)=(β1+β2+β3)×WN=WN
(3)
因為WB=WG+WA,所以WB>WG恒成立,通常令WN=0,不論βi(i=1,2,3)取何值,總存在p(GF)>p(BF)>p(NF)。簇內節點通過多輪博弈剔除不融合節點,降低節點能耗。
2.2 基于貝葉斯理論的數據融合
通過博弈論選取低能耗節點的方式不能保證采集數據均可靠,因此簇頭需通過置信距離篩選可靠數據,提高精確度。置信距離[12]基于預判測量數據與實際數值的緊密程度,確保采集數據接近實際結果。令xi、xj為一次測量中第i個和第j個節點的輸出,且i (4) 其中,分母用作歸一化處理,分子中的概率密度函數定義如下: (5) 效益函數最大值p(GF)作為權重代入概率密度函數,確保節點在善意融合的前提下得到有效數據。當xi=xj時,dij=0;當xi≠xj時,dij∈(0,1)。定義二值變量rij為第i個節點輸出數據對第j個節點輸出數據的支持程度,通過融合結果確定閾值α與rij,具體公式如下: (6) 其中,1表示第i個節點的輸出數據支持第j個節點的輸出數據;0表示第i個節點的輸出數據不支持第j個節點的輸出數據。 假設節點的臨界數為m,對n個節點中任意兩個節點采集的數據計算置信距離得到m×m的二值關系矩陣,表示節點輸出數據間的相互支持程度,篩選出l個有效數據。 (7) (8) DFABGT算法流程如圖2所示,具體步驟如下: 步驟1在一輪博弈中,節點從善意融合、惡意融合與不融合中選擇一個策略,依據能耗與收益計算效益函數。 步驟2通過效益函數值剔除不融合節點降低能耗。 步驟3將效益函數最大值作為權重代入置信距離公式,確保參與融合的節點均是善意融合且相互支持度最高。 步驟4依據融合結果確定閾值,將置信距離向量和閾值進行比較得到二值關系向量,構成二值關系矩陣。 步驟5由二值關系變量剔除小于閾值的置信距離值并且篩選有效數據,簇頭節點將有效數據傳輸給Sink節點。 步驟6Sink節點采用貝葉斯理論融合數據得到融合結果。 步驟7為避免篩選善意或惡意融合節點,需要重復上述步驟完成多輪博弈,直至剩余節點均不融合時為止。 圖2 DFABGT算法流程 將100個節點隨機分布在200 m×200 m中,Sink節點部署在(100 m,100 m)處,處于集群中心且剩余能量最大的節點設置為簇頭[14]。在OPNET仿真環境[15]下對DFABGT算法與E-CPDA算法、MGDAA算法及Megrez算法進行對比,仿真參數如表2所示。 表2 仿真參數設置 依據文獻[16]中數據精確度定義,數據精確度等于融合前后的數據累和之比。考慮到貝葉斯理論,本文采用均值與方差作為判斷融合結果精確度k的依據,具體計算如下: (9) 圖3 數據融合算法的融合結果精確度比較 由圖3可知,DFABGT算法、E-CPDA算法、MGDAA算法與Megrez算法的融合精確度隨著節點數的增多均呈上升趨勢。在傳感器節點數為10~90時,DFABGT算法相比E-CPDA算法、MGDAA算法與Megrez算法精確度上升均值為3.9%、21.2%和12.1%。E-CPDA算法通過降低節點在通信過程中的碰撞幾率提高精確度,但其未篩選數據;MGDAA算法通過改變簇結構冗余度和結構變化度從而破壞原始數據;Megrez算法中的壓縮和重構過程破壞了原始數據;DFABGT算法在篩選原始數據時并沒有破壞和構造數據,因此其精確度高于其他算法。 本文在無線傳感網中采用簡單的能耗模型[17],忽略節點在計算、存儲等過程中的能耗,僅計算節點隨著通信時間增加所消耗的能量。假設節點傳輸lbit數據經過的距離為d(20≤d≤25),數據融合過程中的節點能耗公式如下: (10) ERx_elec(l)=lEelec (11) 其中,ETx(l,d)為發送端經過距離d發送lbit數據的能耗,ERx_elec(l)為接收端接收lbit數據的能耗,d0=25 m為閾值,Eelec為節點收發每比特數據的能耗,εfsd2與εmpd4為信號自由空間模型和多徑衰減模型中信號放大器的能耗參數[18]。當發送端與接收端的距離小于閾值時,采用自由空間的通信方式,發送端能耗與距離的平方成正比;否則采用多徑衰減的通信方式,發送端能耗與距離的4次方成正比。 假設融合單位比特數據的能耗為EDA,由此可知EDA的取值范圍為(0,ETx(l,d)+ERx_elec(l))[19],那么善意融合的能耗取值范圍為(0,lEDA),惡意融合的能耗總是大于善意融合的能耗,而不融合的能耗為0。節點能耗的變化曲線,如圖4所示。 圖4 數據融合算法的節點能耗比較 由圖4可知,DFABGT算法與E-CPDA算法、MGDAA算法和Megrez算法比較,節點能耗分別降低28%、22%和19%。E-CPDA算法通過減少通信傳輸量降低能耗,導致存在額外簇結構的能耗;MGDAA算法與Megrez算法以節點能耗為代價換取數據精確度,但卻未兼顧節點能耗問題,而DFABGT算法通過融合能耗進行博弈來降低節點能耗,且未產生額外能耗。綜上,DFABGT算法的能耗低于其他算法。 網絡生命周期用于衡量負載均衡情況,本文采用文獻[20]的定義,認為網絡生命周期為首個節點的失效時間。網絡中節點存活率的變化情況如圖5所示。 圖5 數據融合算法的網絡生命周期比較 由圖5可知,DFABGT算法與E-CPDA算法、MGDAA算法和Megrez算法進行比較,網絡生命周期分別延長5%、3.1%和4.8%。E-CPDA算法、MGDAA算法和Megrez算法未篩選節點與數據,因此增加了能耗,且E-CPDA算法增加了簇結構的能耗,而DFBAGT算法通過選取節點、篩選數據,大幅度降低節點能量的消耗,使得節點存活率下降幅度低于其他算法。綜上,DFABGT算法的網絡生命周期更長。 本文從提高數據精確度和降低節點能耗兩方面著手,提出基于博弈論的數據融合算法,簇內節點以收益和能耗為效益函數的輸入參數進行博弈。通過效益函數最大值選取低能耗節點,對這些節點進行置信距離的計算來篩選有效數據參與融合處理。簇頭將有效數據傳輸到Sink節點,由Sink節點采用貝葉斯理論融合數據。實驗結果表明,本文算法能有效提高數據精確度,降低節點能耗,延長網絡生命周期。下一步將考慮數據的安全隱私特性,在實現數據精確融合的同時保障數據安全。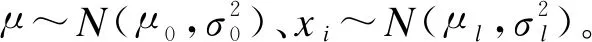
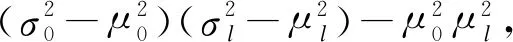
2.3 DFABGT算法實現
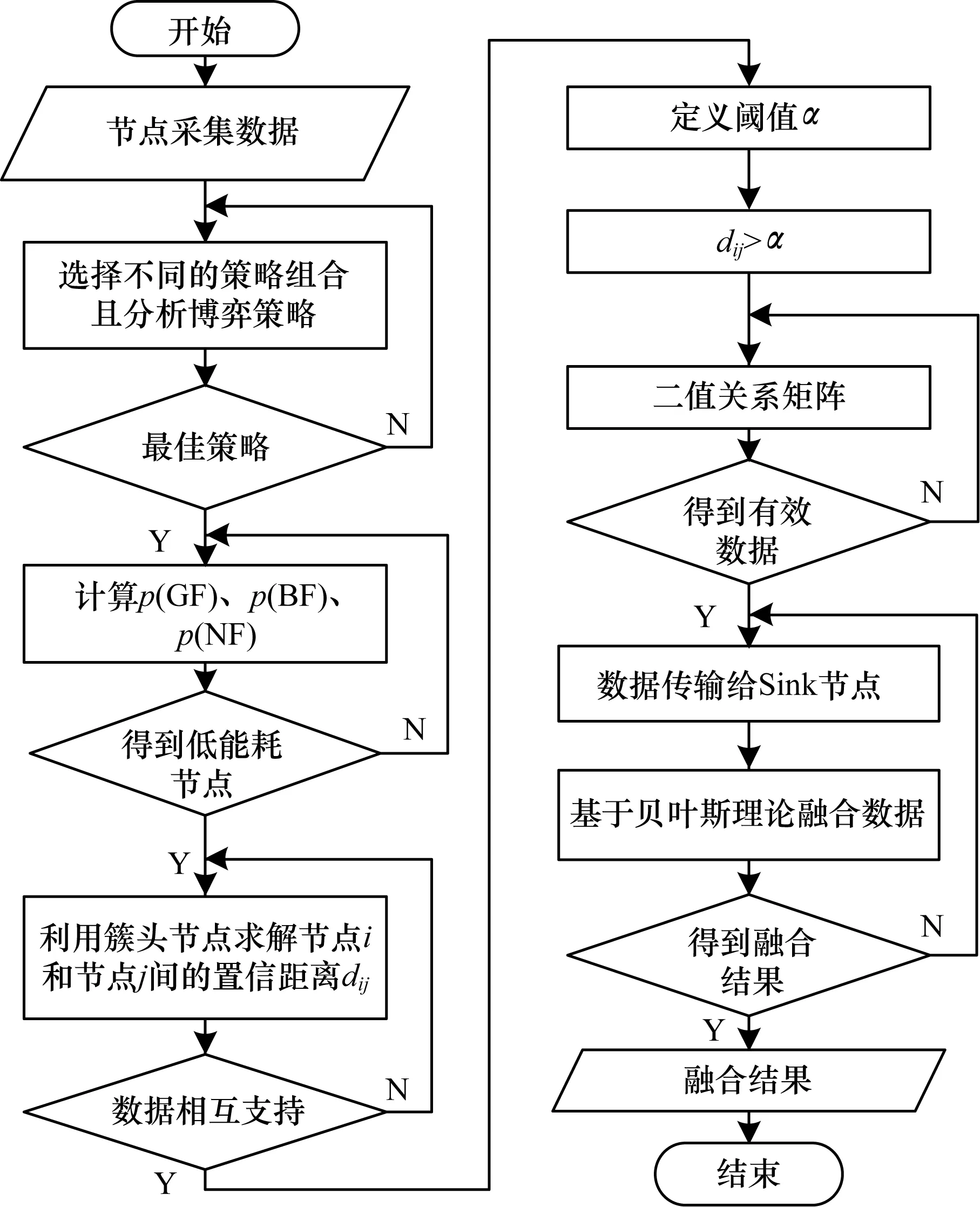
3 算法仿真與性能分析
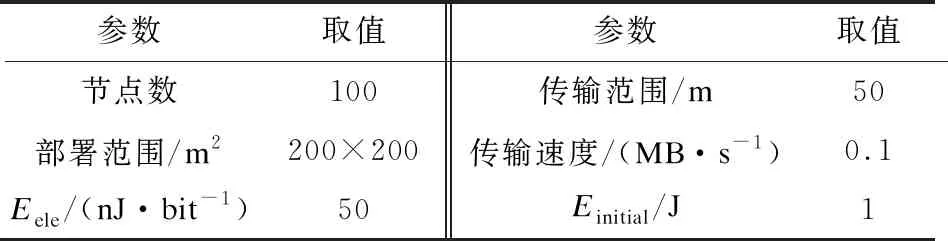
3.1 數據精確度
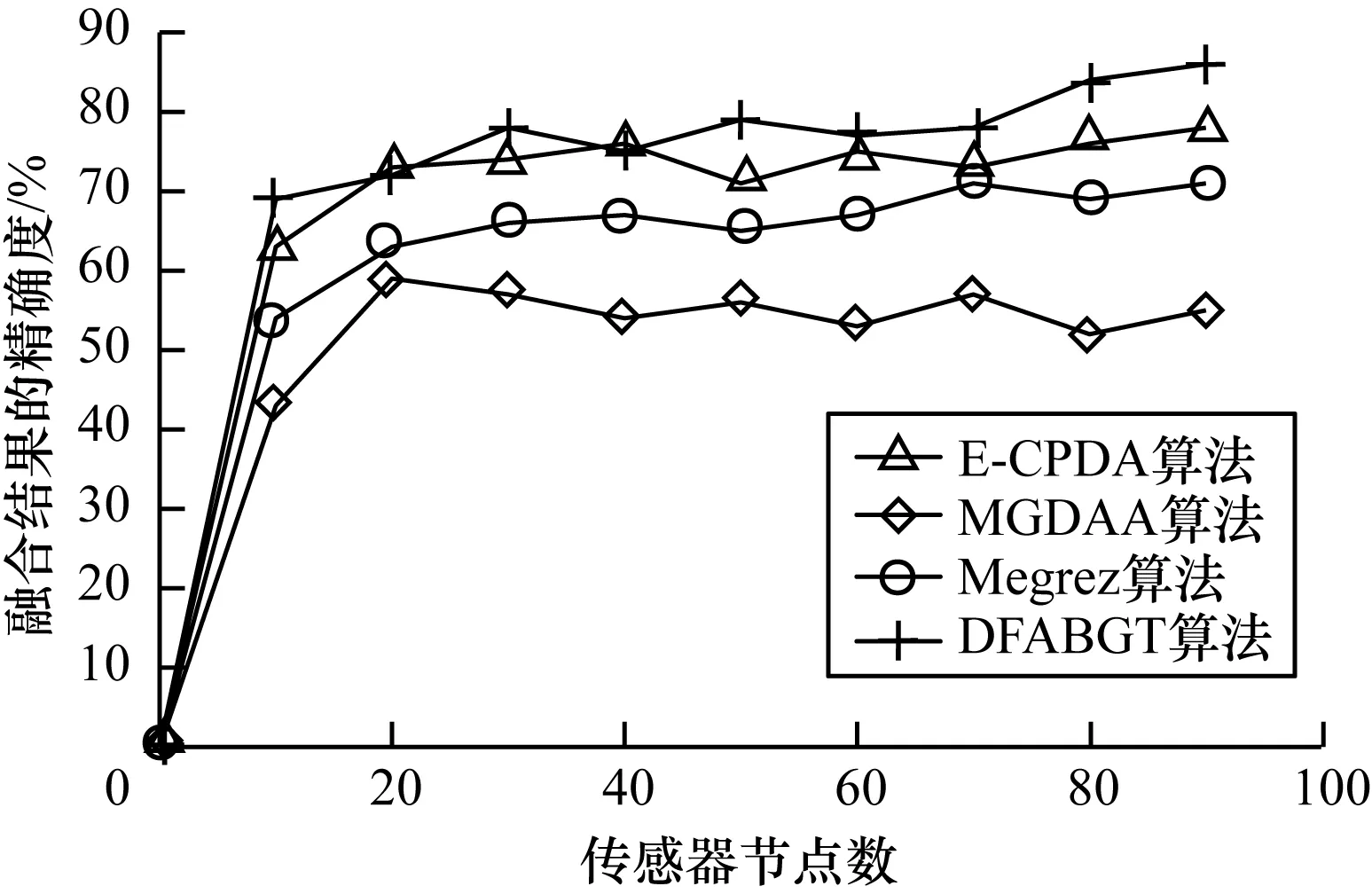
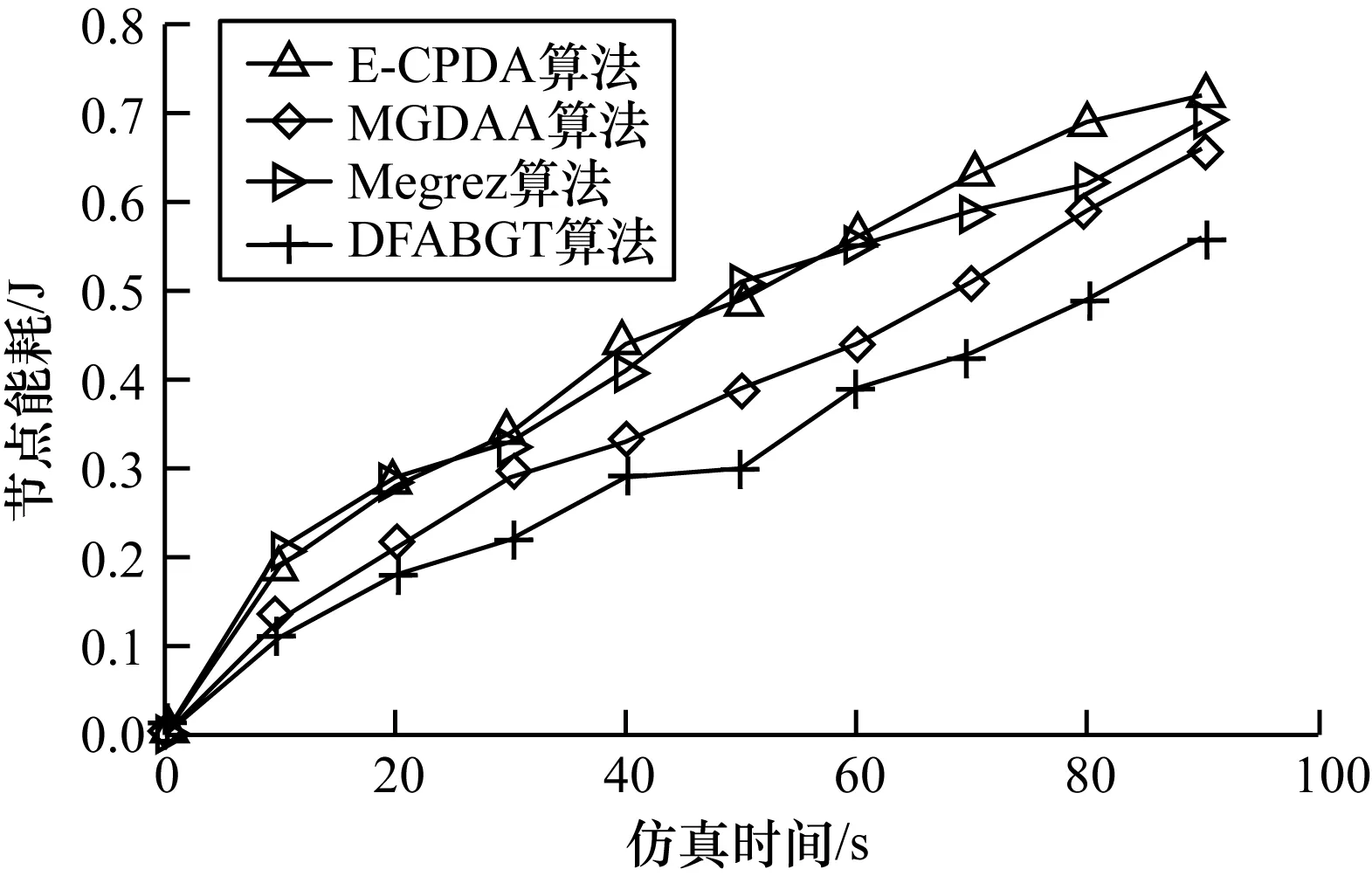
3.2 節點能耗
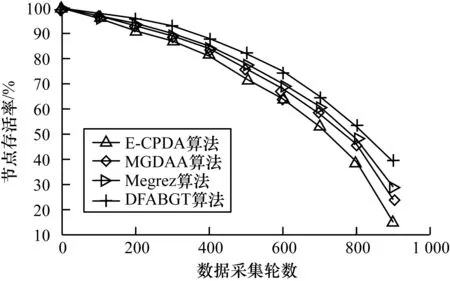
3.3 網絡生命周期
4 結束語

