單向加勁矩形板面內振動特性分析

王 磊 安景峰 徐秀麗 周 叮 胡朝斌，*

（1.南京工業大學土木工程學院，南京211816；2.江蘇省交通工程建設局，南京210004）

0 引 言

在土木、航空航天等工程中，矩形板是常見的構件。為提高板的承載力和穩定性，加勁板構件［1］被廣泛使用，板的振動特性因加勁而發生變化。

在很多實際工程應用中，例如，在土木工程中，由于施工與安裝不準確所帶來的誤差可能會引起加勁板結構產生面內振動，對結構的可靠性和安全性造成一定的影響。因此，面內振動對于加勁板結構的穩定性有著重要的作用。對加勁矩形板面內振動特性的研究，大多采用有限元數值計算或試驗測試方法進行分析。裴然等［2］采用能量法研究了彈性約束邊界條件下矩形板的面內振動特性。Shi等［3］研究了一般邊界條件下環形板的面內振動特性，通過對邊界條件特殊化處理，利用Rayleigh-Ritz法得到改進的面內振動傅里葉級數解。周叮［4］用傳遞矩陣法研究了折線形梁的面內振動特性。馬牛靜等［5］研究了四邊簡支加勁矩形板的面內振動特性。劉文光等［6］采用有限元方法研究了加勁薄板的自由振動特性。李守娟和徐偉［7］采用有限元法研究了附加集中質量加勁板的自由振動特性。Cho［7］用有限單元法及假定模態法研究了加勁板結構的固有模態。Sahoo［8］采用變分法研究了加勁板的非線性振動特性。Rao等［9］將加勁矩形板切分為加強筋和均厚度的矩形板，加強筋可以在板的任意位置，通過Lagrange方程求解加勁板的固有振動頻率。Barrette等［10］采用重三角級數法研究了加勁板的自由振動特性。Fernandes和Neto［11］采用邊界元法（BEM）法分析了由不同材料組成的加勁板的耦合拉伸-彎曲問題。Aksu［12］將有限差分法與變分原理相結合研究偏心加勁板的振動特性，分析了板和加強筋面內變形對加勁板橫向振動特性的影響。杜菲等［13］采用Rayleigh-Ritz法求解四邊固支加勁板的固有頻率，計算結果與實驗值的對比顯示了很好的一致性。Gordo等［14］研究了單軸壓縮載荷下加勁板的極限強度，分析了U型加勁形式對加勁板性能的影響。石楚千等［15］研究了不同筋條剛度下復材加勁板剪切穩定性。本文采用能量法在保證分析過程正確性的同時又簡化了對加勁板面內振動的數值計算過程，為實際工程應用提供理論計算依據，為實驗分析提供參照。

一般情況下板的平面尺寸比厚度要大很多，因此可以使用平面應力理論對其進行面內振動分析；加強筋的長度比其高度與寬度均大得多，因此可以用歐拉梁理論對其進行面內振動分析。本文將典型邊界條件下的單向加勁矩形板切分為矩形板和加強筋兩個部分，利用第一類Chebyshev多項式構造矩形板的位移試函數，由Chebyshev-Ritz［16］法得到加勁矩形板的面內振動特征方程。

1 面內振動方程

圖1為一單向加勁矩形板，矩形板下表面支承有P根等距分布的加強筋。其中矩形板的長寬分別為a、b，厚度為h；加強筋的長度為a，高度和寬度分別為h0和b0。建立如圖所示的坐標系，加勁板中任一點沿x、y方向的位移分別為u、v。現將加勁板沿交界面切分為矩形板和加強筋，分別進行分析。

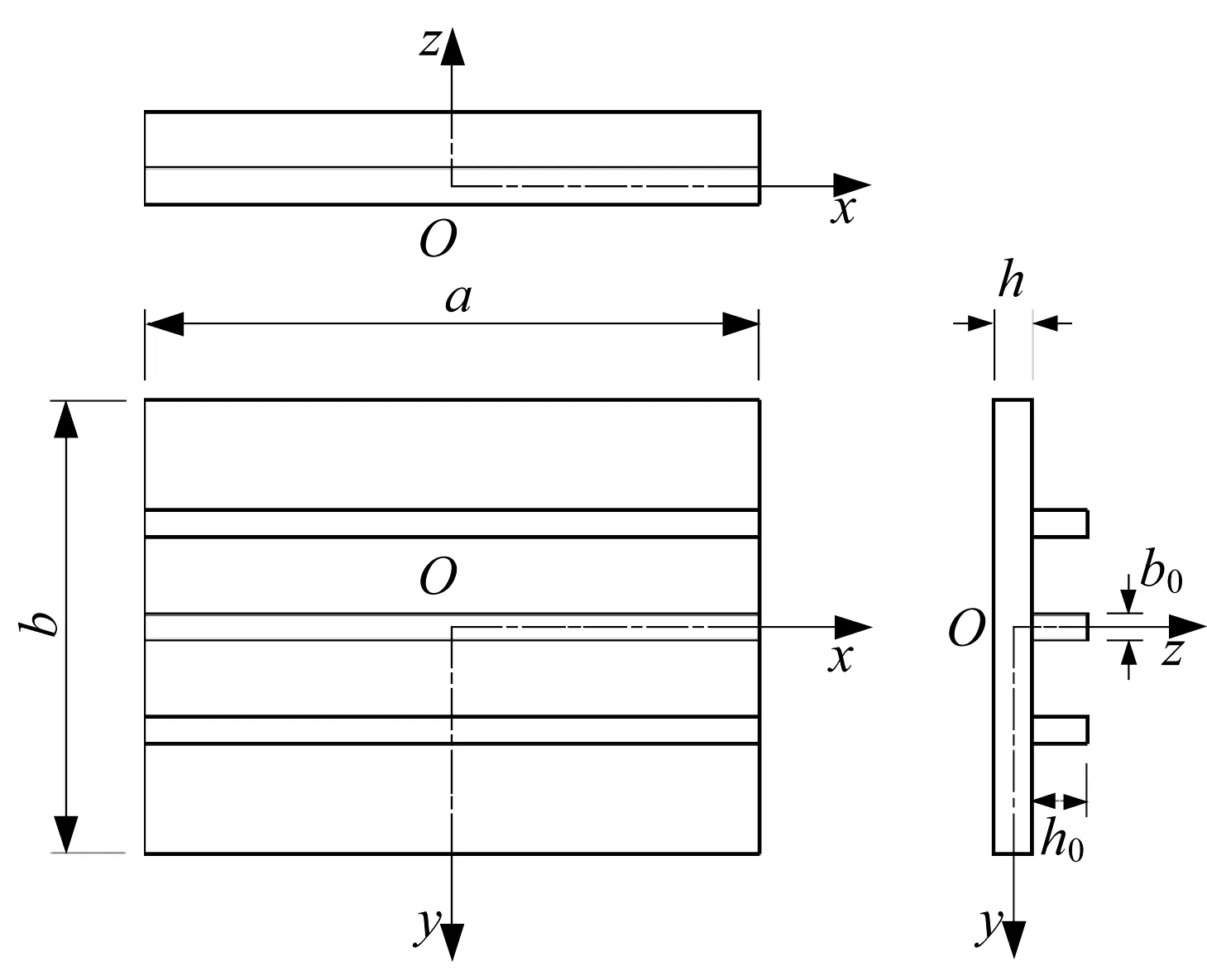
圖1 加勁矩形板模型Fig.1 Analytical model of stiffened rectangular plate

1.1 矩形板的面內振動方程

與橫向彎曲不同，矩形板的面內變形涉及x和y兩個方向上的位移，因此矩形板面內振動的形變勢能與動能為

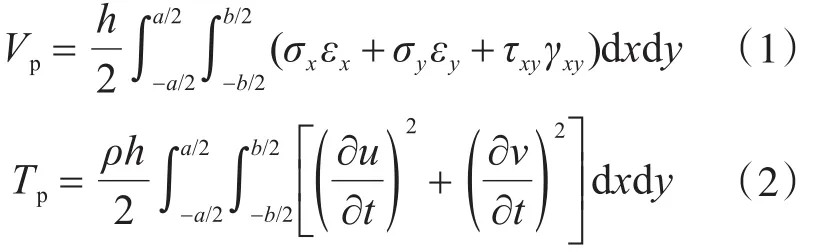
式中：εx、εy分別表示沿x和y軸方向的正應變；γxy為切應變；σx、σy分別表示沿x和y軸方向的正應力；τxy為切應力；ρ為矩形板的密度。

根據平面應力理論，矩形板面內應變和面內應力可分別用位移表示為

式中：E為矩形板的楊氏模量；μ為矩形板的泊松比。

矩形板在x、y方向面內振動的位移函數分量可表示為

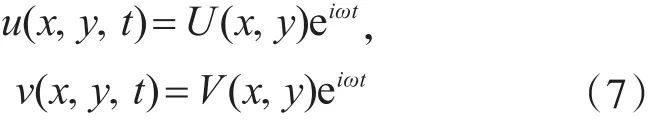
為了數學表述的方便，引入如下的無量綱坐標：

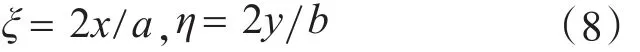
將式（3）-式（8）代入式（1）和式（2），可分別得矩形板的形變勢能與動能為

其中，λ=a∕b為板的長寬比。

用第一類切比雪夫多項式分別構造矩形板在x和y方向上的位移試函數為

式中，φu（ξ）、φv（ξ）和fu（η）、fv（η）分別為x和y方向的邊界函數分量，以保證式（11）滿足一定的幾何邊界條件，如表1所示，PS（x）是一維s階第一類切比雪夫多項式，用余弦形式表示為

Ps(x)=cos[(s-1)arccos(x)]，(s=1，2，3，…)（12）

表1 不同邊界條件下的邊界函數分量Table 1 Boundary characteristic function components for different boundary conditions

1.2 加強筋的面內振動方程

由于加強筋的長度比其截面尺寸大得多，因此可用歐拉梁理論對其進行面內振動分析。不失一般性，考慮第k條加強筋，設其在板上的位置為y=yk。由于加強筋與矩形板交界面上滿足位移連續，因此，加強筋分別考慮加強筋沿x方向上的軸向變形以及沿y方向的彎曲變形，則其形變勢能與動能為

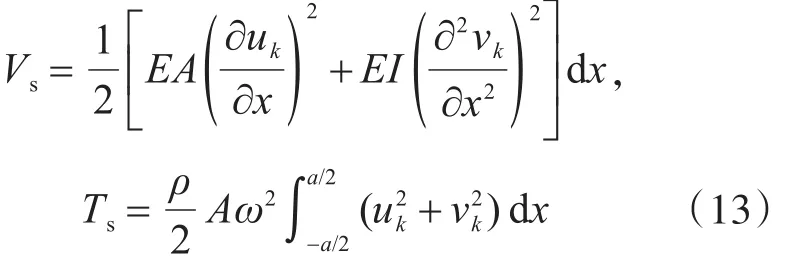
式中：uk和vk為第k條加強筋在x和y方向上的位移；A為加強筋的截面面積；EI為加強筋對其中性面的彎曲剛度。

考慮到板和加強筋在連接處的位移連續條件，有

式中，Uk和Vk分別為第k條加強筋在x和y方向上的位移試函數；ηk=2yk∕b為第k條加強筋在板上的無量綱位置。

將式（11）代入式（10）得加強筋的形變勢能與動能為

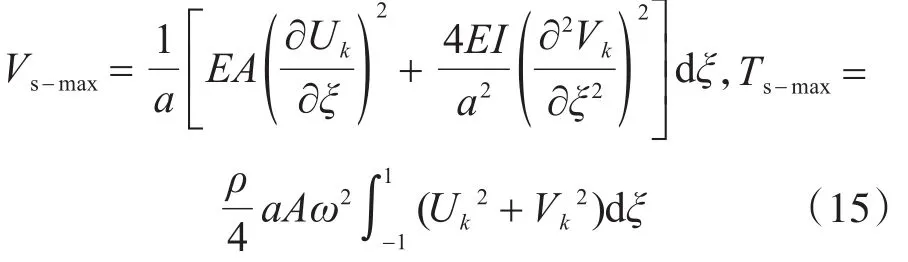
1.3 加勁板的面內振動方程

根據以上分析，單向加勁矩形板面內振動的勢能與動能分別為

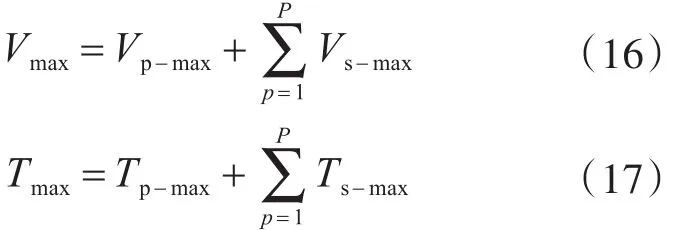
定義能量泛函為

由Rayleigh-Ritz法得：

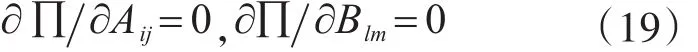
將式（9）-式（17）代入式（18），可得加勁板面內自由振動的頻率方程為

｛A｝、｛B｝為未知系數的列向量，其表達式為

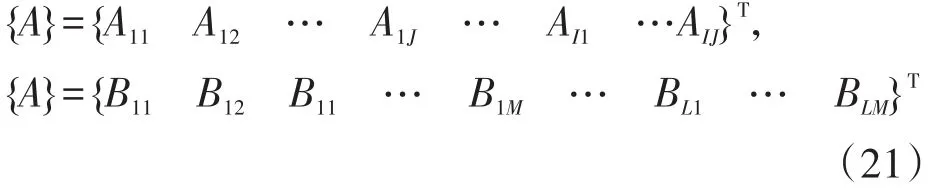
式中，

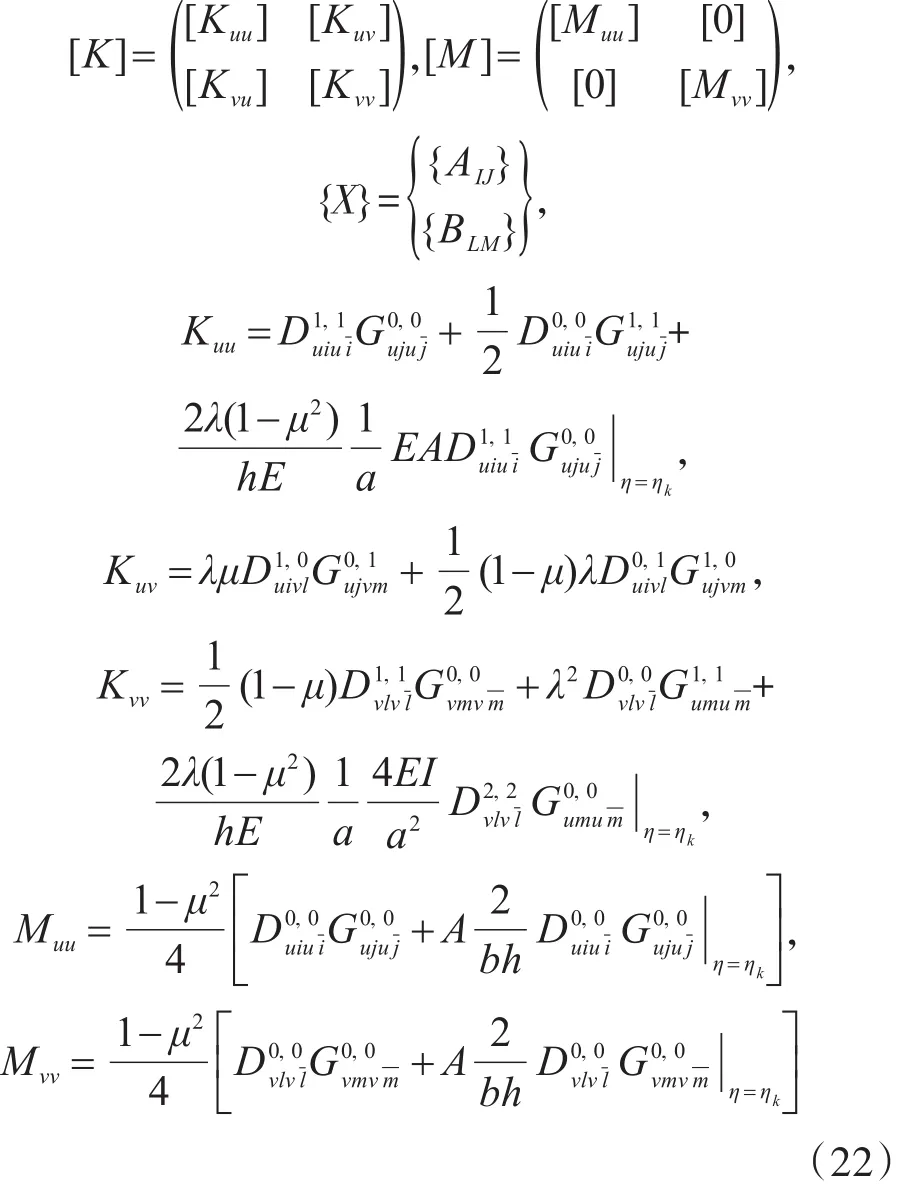
這里，

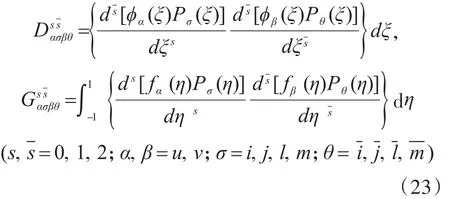
通過求解特征方程式（20），可以得到加勁矩形板面內振動任意階次無量綱特征頻率和相應的特征模態系數。若不考慮式（16）和式（17）中加強筋的作用，則可以得到矩形板面內振動任意階次無量綱特征頻率和相應的特征模態系數。

2 收斂性分析和比較研究

考察一對邊固定另兩對邊自由、含一根加強筋的加勁方板。方板和加強筋由同種材料組成，其彈性模量 E=40 GPa，密度 ρ=2 000 kg∕m3，泊松比μ=0.3。方板的邊長分別為a=b=5 m，板厚h=0.1 m。加強筋位于y=0處，其截面尺寸分別取b0×h0=0.1 m×0.2 m、0.1 m×0.4 m、0.2 m×0.4 m。表2給出了加勁方板面內自由振動前六階無量綱頻率。表2可以看出本文方法具有快速收斂的特性，在截斷級數項取到20×20時，可保證前三位有效數字相同，故在隨后的計算中級數項全部取為20×20。

一般而言，一些數值方法如有限單元法可以用來計算本文問題。但是有限元方法作為一種數值方法，其精度還有待驗證。表3給出本文解與有限元解的比較。有限元模擬使用ANSYS軟件，方板采用殼單元SHEEL181，加強筋采用梁單元BEAM188。從表3可以看出，前六階無量綱頻率的有限元解與本文理論解吻合很好，其最大誤差只有1.517%，驗證了有限元方法的精度。

在本文方法中，獲得振動頻率后，將方程式（20）求解得到的特征模態系數代入到位移方程式（11）中，得到加勁板各點的位移量，進而可以獲得各階次振動頻率下的模態圖。圖2是邊界條件為兩對邊固定另兩對邊自由（CFCF）的單向加勁方板面內振動的前四階模態圖。

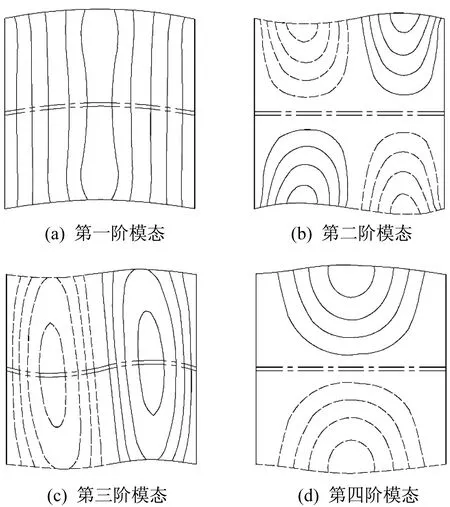
圖2 兩對邊固定另兩對邊自由（CFCF）單向加勁方板的前四階模態圖Fig.2 The first four modes of square plate with CFCF boundary conditions and a stiffener

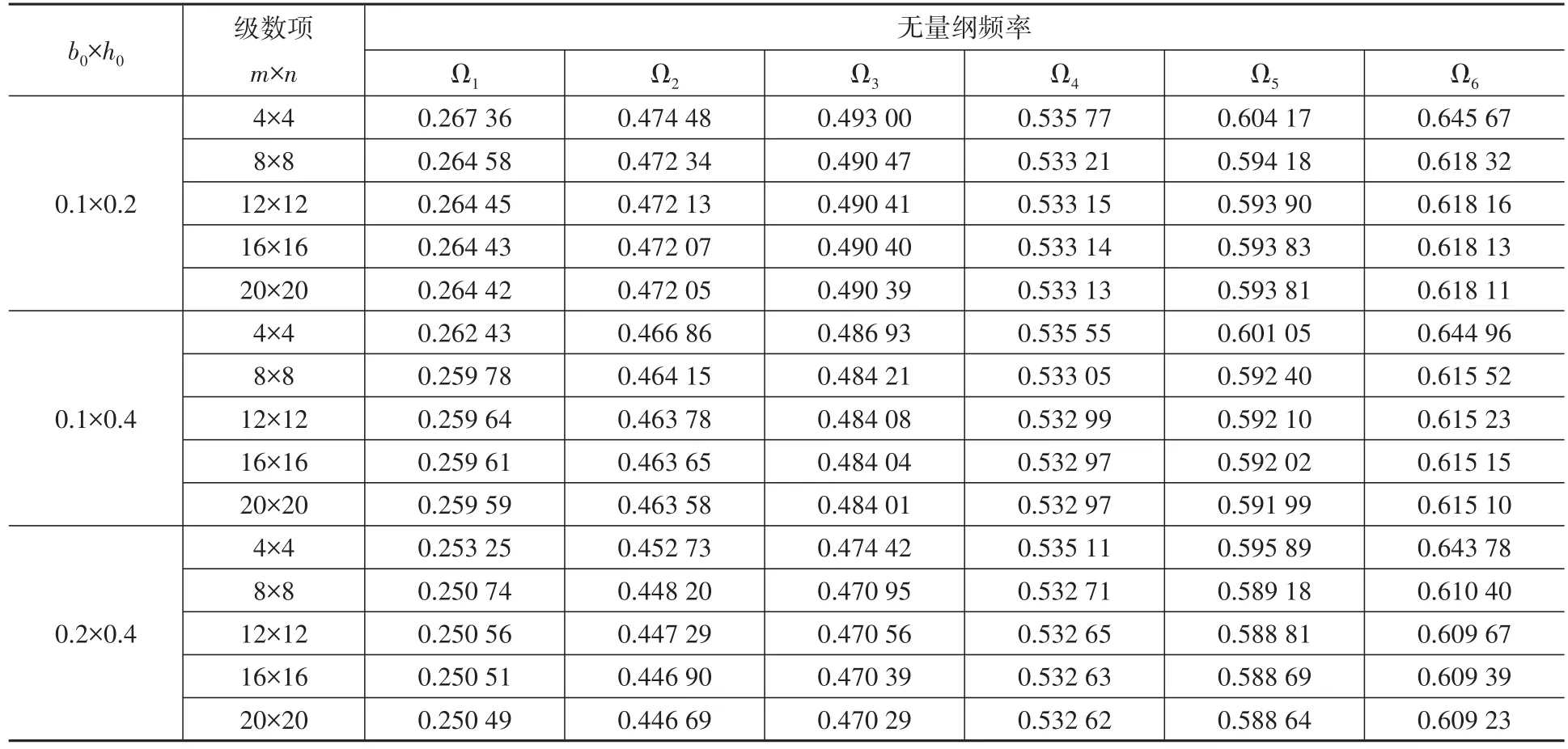
表2 對邊固定另兩邊自由加勁板面內自由振動前六階頻率參數的收斂性Table 2 Convergence of first six frequency parameters for stiffened plate with CFCFboundary conditions

表3 本文解與有限元結果的比較Table 3 Comparisons of present solutions and FE results

3 參數分析

現研究加強筋寬度與板寬比值（b0/b）和加強筋位置對頻率的影響。設加強筋的寬高比b0∕h0=1。圖 3為加強筋在不同位置下（η=0、0.2、0.4、0.6、0.8），b0/b的變化對前四階無量綱固有頻率的影響。

從圖3中看到，隨著加強筋寬度與板寬比值的增大，無量綱固有頻率逐漸減小。加強筋越靠近邊緣，固有頻率越低，且加強筋位置的影響隨頻率階數的增加而顯著增大。

4 結 論

本文研究了典型邊界條件下單向加勁矩形板的面內振動特性。將加勁板沿交界面切分為矩形板、加強筋兩部分，分別建立其面內振動能量方程，根據二者在交界面上的位移連續性條件，得到整個加勁板面內振動的任意階固有頻率。最后以對邊固定另兩邊自由的加勁方板為例進行參數分析。本文的主要結論為：

（1）使用第一類Chebyshev多項式構造任意邊界條件下加勁板的位移試函數優勢明顯，數值結果證明了本方法的收斂性，與有限元軟件的對比證明了本方法的精確性。

（2）將加勁板分為矩形薄板與加強筋，采用平面應力理論和歐拉梁理論分別對其進行面內振動分析，模型科學合理，減小了因建模不準確帶來的誤差。

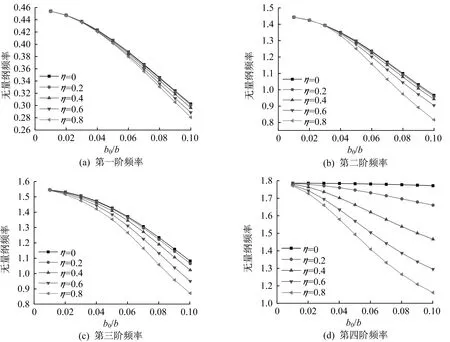
圖3 不同位置下加強筋的寬度與板寬之比對前四階無量綱頻率的影響Fig.3 Effects of stiffener-width-to-plate-width ratio on the first four non-dimensional frequencies of plate stiffened at different positions

（3）加強筋在板下的位置和加強筋寬度與板寬的比值對加勁板的面內振動特性有明顯影響，為后續實際工程中加強筋尺寸和位置優化設計的研究奠定良好基礎。