基于評估使用年限的既有結(jié)構(gòu)可靠度評定實用方法

蔣利學 王卓琳

（上海市建筑科學研究院有限公司上海市工程結(jié)構(gòu)安全重點實驗室，上海200032）

0 引 言

既有結(jié)構(gòu)評定不同于新建結(jié)構(gòu)設(shè)計的一個顯著特點是，既有結(jié)構(gòu)的耐久性問題更加突出，特別是接近或超過設(shè)計使用年限的結(jié)構(gòu)，這個問題尤其應(yīng)引起重視。我國國家標準《工程結(jié)構(gòu)可靠性設(shè)計統(tǒng)一標準》（GB 50153—2008）［1］將結(jié)構(gòu)極限狀態(tài)分為承載能力極限狀態(tài)和正常使用極限狀態(tài)兩類，并明確將耐久性劃入正常使用極限狀態(tài)范疇。新修訂的國家標準《建筑結(jié)構(gòu)可靠性設(shè)計統(tǒng)一標準》（GB 50068—2018）[2]則將結(jié)構(gòu)極限狀態(tài)分為承載能力極限狀態(tài)、正常使用極限狀態(tài)和耐久性極限狀態(tài)三類。該標準指出：理論上講，足夠的耐久性要求已包含在一段時間內(nèi)的安全性和適用性要求中。但出于實用的原因，需增加與耐久性有關(guān)的極限狀態(tài)內(nèi)容。廣義的耐久性極限狀態(tài)包含影響結(jié)構(gòu)初始耐久性能的狀態(tài)、影響結(jié)構(gòu)正常使用的狀態(tài)和影響結(jié)構(gòu)安全性能的狀態(tài)三類。該標準首次引入的耐久性極限狀態(tài)系指影響結(jié)構(gòu)初始耐久性能的狀態(tài)，這也與國際標準《結(jié)構(gòu)可靠性統(tǒng)一原則》（ISO 2394：2015）[3]等接軌。后文將GB 50153—2008和GB 50068—2018共同簡稱為“我國統(tǒng)一標準”。

一般而言，耐久性引起的問題首先體現(xiàn)為裂縫、變形、表面剝落等影響正常使用的問題，只要將這些問題處理好，使其不致影響正常使用，則其安全性降低不致使結(jié)構(gòu)構(gòu)件達到或超過承載能力極限狀態(tài)。因此，對大多數(shù)建筑結(jié)構(gòu)而言，將耐久性問題設(shè)定為適用性范疇的目標是合適的。但某些情況下耐久性問題可能成為安全性范疇的問題，如：一組相同環(huán)境下混凝土構(gòu)件的耐久性試驗結(jié)果表明，對于混凝土梁、柱類構(gòu)件，銹脹裂縫剛出現(xiàn)時的角部18縱筋截面損失率小于2%，而φ6.5箍筋的截面損失率大于15%［4］。保護層厚度較大且鋼筋較細的板類構(gòu)件，往往鋼筋截面損失率超過10%時才可能出現(xiàn)銹脹裂縫，這已嚴重影響構(gòu)件承載力而危及結(jié)構(gòu)安全［5］。對一片240 mm厚磚墻，若單側(cè)發(fā)生平均深度為15 mm的風化，則因截面削弱和偏心距增大的雙重影響，其抗壓承載力可能下降10%以上。對這些構(gòu)件，耐久性引起的安全性問題上升為主要問題。

另一方面，結(jié)構(gòu)耐久性屬正常使用狀態(tài)范疇問題的定性，使人們形成了耐久性僅僅影響正常使用、不會影響安全性的認識，可能會弱化耐久性在業(yè)主和工程技術(shù)人員心中的重要性認識，從而對設(shè)計、建造和可靠性評定過程中的耐久性措施、使用過程中的正常檢查維護措施等沒有引起充分的重視，或者錯過了采取措施的最佳時機，可能導致耐久性問題引發(fā)結(jié)構(gòu)安全風險。

因此，研究耐久性對結(jié)構(gòu)安全性的影響，在既有結(jié)構(gòu)可靠度評定中考慮結(jié)構(gòu)抗力退化的影響，具有重要的理論和工程實踐意義。

結(jié)構(gòu)可靠性是結(jié)構(gòu)在規(guī)定的時間內(nèi)，在規(guī)定的條件下完成預(yù)定功能的能力［1-2］。因此，結(jié)構(gòu)可靠性必須對應(yīng)于某個“規(guī)定的時間”，無論對于新建結(jié)構(gòu)設(shè)計還是既有結(jié)構(gòu)評定，不明確“規(guī)定的時間”談可靠性是失去意義的。2000年1月頒布的國務(wù)院令《建設(shè)工程質(zhì)量管理條例》明確規(guī)定，無論是新建結(jié)構(gòu)設(shè)計還是既有結(jié)構(gòu)評定，均必須明確合理使用年限。自2000年以來，我國統(tǒng)一標準［1-2］已將明確設(shè)計使用年限列入強制性條文。對新建結(jié)構(gòu)設(shè)計而言，法律法規(guī)和技術(shù)標準對“必須明確設(shè)計使用年限”的規(guī)定，已經(jīng)轉(zhuǎn)化為廣大設(shè)計人員和其他從業(yè)人員的自覺行動。但我國有關(guān)既有結(jié)構(gòu)評定的技術(shù)標準，或者未要求確定評估使用年限［6］，或者提出了要求但具體規(guī)定不明確［4，7］。我國目前很多既有結(jié)構(gòu)可靠性評定報告既不明確評估使用年限，也不對結(jié)構(gòu)耐久性進行分析評估。這樣，如果某既有結(jié)構(gòu)在經(jīng)可靠性評定后的若干年內(nèi)發(fā)生了安全性問題，評定單位和評定人員是否應(yīng)承擔責任，還是承擔無限期責任，沒有明確答案，下一次可靠性評定應(yīng)在什么時間實施也不明確，這與可靠性評定的主要目標明顯相背。

我國統(tǒng)一標準規(guī)定的目標可靠指標對應(yīng)于設(shè)計使用年限內(nèi)的允許累積失效概率。也就是說，設(shè)計使用年限不同時，結(jié)構(gòu)的實際累積失效概率及其對應(yīng)的實際可靠指標也是不同的，其允許累積失效概率及其對應(yīng)的目標可靠指標也應(yīng)作出相應(yīng)改變。早在1990年，王光遠院士就提出服役結(jié)構(gòu)的動態(tài)可靠度的概念，并提出用三個系數(shù)對新建結(jié)構(gòu)可靠度進行修正以獲得服役結(jié)構(gòu)動態(tài)可靠度的設(shè)想［8］：一是經(jīng)歷系數(shù)，即根據(jù)評定時結(jié)構(gòu)的檢測檢查結(jié)果（如材料強度超強等）對可靠度的修正系數(shù)；二是結(jié)構(gòu)抗力調(diào)整系數(shù)；三是荷載效應(yīng)調(diào)整系數(shù)。他還特別指出：認為服役結(jié)構(gòu)的抗力不斷退化故其可靠度也不斷下降的觀點是錯誤的，這是不考慮評估使用年限變化引起的，只有評估使用年限始終保持與設(shè)計使用年限一致時才是成立的。

本文在總結(jié)分析國內(nèi)外關(guān)于考慮抗力和荷載效應(yīng)時變性的結(jié)構(gòu)可靠度研究成果的基礎(chǔ)上，提出了既有結(jié)構(gòu)基于評估使用年限的可靠度評定實用方法。

1 國內(nèi)外關(guān)于結(jié)構(gòu)時變可靠度研究成果的分析

我國現(xiàn)行結(jié)構(gòu)設(shè)計規(guī)范中的可靠度分析模型尚未充分考慮時間變化的因素，是一個靜態(tài)模型［9］。引起結(jié)構(gòu)在服役期間可靠度動態(tài)變化的因素主要來自兩個方面：一是因材料耐久性引起的結(jié)構(gòu)抗力退化；二是后續(xù)使用年限變化引起的荷載效應(yīng)變化。當然，對既有結(jié)構(gòu)進行周期性檢查維護、可靠性評定和加固，也會改變結(jié)構(gòu)的動態(tài)可靠度。單獨研究使用年限變化引起荷載效應(yīng)變化的成果很多，這里不做專門分析，下面主要分析關(guān)于考慮抗力退化或同時考慮抗力退化和荷載效應(yīng)變化的時變可靠度研究成果。

Mori等［10］研究了預(yù)測鋼筋混凝土核電站結(jié)構(gòu)使用年限的概率分析方法。其可變荷載隨機過程采用泊松模型，將抗力隨機過程R（t）表示為式（1）所示的服役期起始點抗力隨機變量R0乘以一個確定性的抗力衰減函數(shù)φ（t）：

這是一個最簡單的隨機過程模型。他們考察了抗力退化率、抗力退化模型（不退化、二次拋物線模型退化、線性模型退化、平方根模型退化）、荷載平均發(fā)生率等因素對單構(gòu)件和簡單結(jié)構(gòu)體系在不同使用年限內(nèi)累積失效概率的影響，以及定期檢查維護對提高后續(xù)使用年限內(nèi)的可靠度的作用。

Mori等還用改進蒙特卡羅方法研究鋼筋混凝土抗力退化結(jié)構(gòu)體系的時變可靠度［11］。研究發(fā)現(xiàn)，重要抽樣變量的平均值和標準差對重要抽樣的效率和精度均有重要影響，采用自適應(yīng)蒙特卡羅模擬過程結(jié)合條件期望方法對該類退化結(jié)構(gòu)體系的時變可靠度進行分析十分有效。不同于簡單蒙特卡羅模擬方法，用自適應(yīng)重要抽樣評估失效概率時模擬精度對失效概率階數(shù)不敏感，因此對失效概率較小的結(jié)構(gòu)用這種方法優(yōu)勢更加明顯。

Enright等［12］在文獻［10］的基礎(chǔ)上，考慮抗力和荷載效應(yīng)的時變性，研究高速公路T形梁的構(gòu)件和體系可靠度。其抗力隨機過程用式（1）表達，可變荷載用泊松過程模擬，并用蒙特卡羅方法分析累積失效概率。他們分析了永久荷載與可變荷載的變異性、可變荷載的發(fā)生率、強度損失率、抗力退化起始時間、抗力校準、退化構(gòu)件數(shù)等參數(shù)對橋梁時變可靠度的影響。該方法可用來預(yù)測混凝土橋梁的使用壽命，并建立該類橋梁基于可靠度的全壽命維護策略。

Dey等［13］提出了一種用于計算脆性結(jié)構(gòu)體系時變可靠度的高效的重要抽樣方法。相對于簡單蒙特卡羅方法，該方法作了如下改進：去除了對許多關(guān)鍵失效序列的乏味枚舉過程，去除了理想化馬爾可夫鏈假定并可考慮破壞狀態(tài)的相關(guān)性，提供了體系失效概率的單值解。該方法分析中考慮了抗力和荷載效應(yīng)的時變性以及周期性維護等因素，比簡單蒙特卡羅法更快獲得真解。

李田和劉西拉［9］提出了一種與我國現(xiàn)行規(guī)范相協(xié)調(diào)的混凝土結(jié)構(gòu)耐久性設(shè)計方法。他們將不同時刻的結(jié)構(gòu)抗力R（t）和荷載效應(yīng)S（t）均作為隨機變量，用蒙特卡羅法直接計算對應(yīng)時刻的可靠度β（t），并用如下公式近似計算耐久性設(shè)計系數(shù)η（t）：

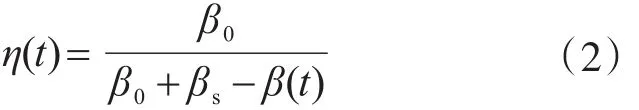
式中：β0為現(xiàn)行規(guī)范的可靠指標；βs為t時刻要求的可靠指標。

通過對北京地區(qū)民用建筑地上混凝土結(jié)構(gòu)的調(diào)查，他們假定鋼筋銹蝕耐久性抗力退化僅是因混凝土強度和鋼筋強度的降低引起，對混凝土和鋼筋強度分別采用式（1）所示的隨機過程模型，并給出了相關(guān)統(tǒng)計參數(shù)的時變模型（相關(guān)參數(shù)含義具體見文獻［9］）：

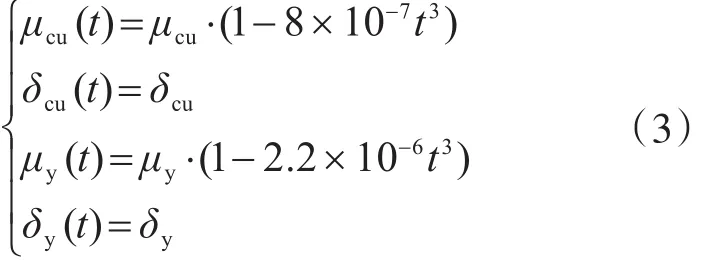
即混凝土和鋼筋強度的平均值衰減曲線是三次曲線，而變異系數(shù)保持初始值不變。他們給出的北京地區(qū)民用建筑地上結(jié)構(gòu)中混凝土梁的動態(tài)可靠指標表達式為

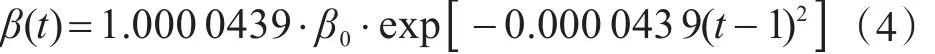
則有：

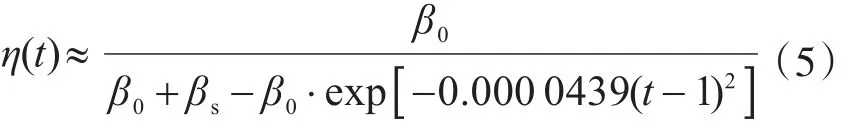
當取βs=β0時，式（5）變?yōu)?/p>

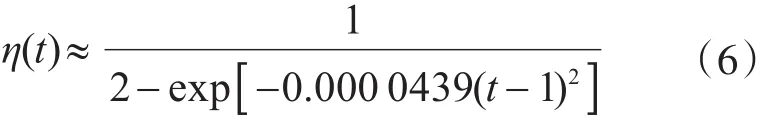
貢金鑫和趙國藩［14］提出了考慮抗力退化的結(jié)構(gòu)可靠度分析方法。由于我國在編制結(jié)構(gòu)設(shè)計統(tǒng)一標準時采用了校準法，只考慮永久荷載和一種可變荷載的基本組合，則基本組合下結(jié)構(gòu)某一狀態(tài)的功能函數(shù)為

式中，G，Q（t）分別為永久荷載效應(yīng)和可變荷載效應(yīng)。

設(shè) QT=maxQ(t)，t∈[0，T]為設(shè)計基準期 T內(nèi)可變荷載效應(yīng)Q（t）的最大值隨機變量，則當不考慮抗力退化時

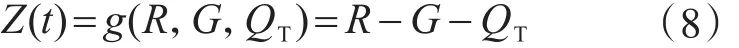
將設(shè)計基準期分為m個相等的時段，并假定Qi服從極值I型分布且各時段的Qi相互獨立。將荷載效應(yīng)隨機過程Q（t）離散化為m個隨機變量Qi的同時，將抗力隨機過程R（t）也離散化為m個隨機變量Ri，Ri的大小取為第i個時段抗力的中值。據(jù)此建立了考慮抗力退化的結(jié)構(gòu)可靠度分析功能函數(shù)：

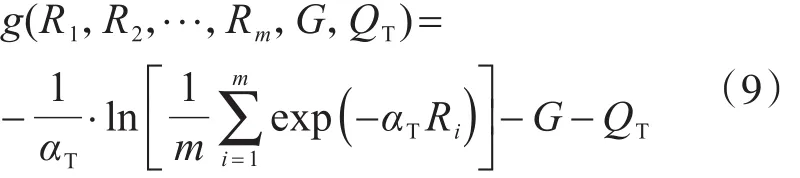
式中，αT為極值I型分布的計算參數(shù)，而R1，R2，…，Rm等m個隨機變量完全相關(guān)。

根據(jù)式（9），可用JC法等一次二階矩方法計算結(jié)構(gòu)可靠指標。

林擁軍等［15］認為，既有結(jié)構(gòu)可靠性評定與新建結(jié)構(gòu)設(shè)計的重要區(qū)別是，兩者的目標使用年限及其起始時刻不同。對起始時刻相同的構(gòu)件，縮短評估使用年限時，其目標可靠指標也應(yīng)相應(yīng)減小。另一方面，隨著服役時間的增長，既有結(jié)構(gòu)的抗力降低，可靠指標相應(yīng)減小，而且抗力下降的速率也會增大，其可靠指標降低的速率也會加快，因此，在相同評估使用年限內(nèi)，不同起始時刻的目標可靠指標也是不一樣的。他們認為，考慮抗力退化的目標可靠指標實際上是評估使用年限內(nèi)起始時刻的最低可靠指標。他們也將抗力隨機過程用式（1）表示，根據(jù)不考慮抗力退化的目標可靠指標［β］和抗力衰減函數(shù)φ（t）計算設(shè)計使用年限Ts結(jié)束時的目標可靠指標［β（Ts）］。對于同一結(jié)構(gòu)的可靠性評定，則令評估使用年限Tc結(jié)束時的目標可靠指標［β（t0+Tc）］=［β（Ts）］，則可以反算評估使用年限起始時刻t0的目標可靠指標［β（t=t0|Tc）］。因此，既有結(jié)構(gòu)構(gòu)件的目標可靠指標是已服役時間t0和評估使用年限Tc的函數(shù)。

由于將結(jié)構(gòu)抗力和荷載效應(yīng)均以隨機過程作為分析模型直接計算結(jié)構(gòu)可靠指標或失效概率十分困難，一般均假定結(jié)構(gòu)抗力為隨機變量，同時將多個荷載組合效應(yīng)近似以它們在設(shè)計使用年限或評估使用年限內(nèi)的最大值（隨機變量）代替，這樣可使結(jié)構(gòu)可靠度計算最終歸結(jié)為隨機變量的概率計算，而荷載效應(yīng)的組合也可作為獨立問題進行研究［16］。國際標準 ISO 2394：2015［3］和我國國家標準［1-2］均采用這種方法。姚繼濤［16］認為，按照荷載的等時段平穩(wěn)二項矩形波過程模型，不同時段的荷載效應(yīng)均應(yīng)是相互獨立的，但我國國家標準采用的荷載效應(yīng)JCSS組合規(guī)則則假定它們完全相關(guān)。這種矛盾使荷載效應(yīng)組合的分析與荷載分析模型不符，而且荷載效應(yīng)組合的分析結(jié)果也會因相關(guān)性增強而導致可靠度分析結(jié)果偏于冒進。為了克服這個缺陷，姚繼濤提出了結(jié)構(gòu)失效概率的時段分析法，建議在荷載效應(yīng)的最小時段內(nèi)計算結(jié)構(gòu)失效概率，并根據(jù)各時段的失效概率推算設(shè)計使用年限內(nèi)的失效概率。當不考慮結(jié)構(gòu)抗力退化，且荷載效應(yīng)是平穩(wěn)的，即荷載效應(yīng)任意時點的概率分布相同時，結(jié)構(gòu)在各時段內(nèi)的失效概率或可靠指標均相等。最小時段內(nèi)的可靠指標采用一次二階矩方法計算。這種以時段可靠度分析為基礎(chǔ)的分析方法不僅符合結(jié)構(gòu)抗力荷載分析模型以及荷載效應(yīng)組合的理論模型，而且不必采用近似的方法進行荷載效應(yīng)組合，并尋找最不利組合。為了克服多維標準正態(tài)分布函數(shù)計算上的困難，姚繼濤提出了一種簡便的計算方法，基本步驟是：將荷載效應(yīng)按照時段長度由小到大的順序，逐層計算可靠指標，將復雜的多維標準正態(tài)分布函數(shù)計算問題轉(zhuǎn)化為等可靠指標、等相關(guān)系數(shù)的多維標準正態(tài)分布函數(shù)的計算問題。將上述方法應(yīng)用于非平穩(wěn)隨機過程的既有結(jié)構(gòu)可靠度分析時，應(yīng)將抗力離散化為等時段的非平穩(wěn)二項矩形波過程，其中對時段的劃分應(yīng)保證時段內(nèi)的抗力強相關(guān)，能夠以時段內(nèi)的最小值作為該時段的抗力，而各時段抗力之間的相關(guān)性根據(jù)實際情況確定。這時，各時段的抗力不僅具有不同的概率分布，而且相互之間也具有不同的相關(guān)系數(shù)。計算時，在形式上將抗力視為荷載效應(yīng)，參與評估使用年限內(nèi)時段數(shù)的排序［16］。

總結(jié)上述研究成果，得到既有結(jié)構(gòu)時變可靠度研究的基本結(jié)論以及作者對時變可靠度的實用分析方法思路如下：

（1）考慮耐久性退化的抗力隨機過程十分復雜，目前研究尚不充分。為結(jié)構(gòu)可靠度分析的方便，絕大多數(shù)學者將抗力退化隨機過程用式（1）所示的服役期起始點抗力隨機變量R0乘以一個確定性的抗力衰減函數(shù)表示，這是最簡單的隨機過程模型。按這個模型，抗力的平均值和標準差按抗力衰減函數(shù)同步退化，故變異系數(shù)保持初始值不變。

（2）同時考慮抗力退化和評估使用年限不同引起的荷載效應(yīng)變化，將抗力和荷載效應(yīng)均作為隨機過程直接計算可靠度，多數(shù)學者采用蒙特卡羅方法或改進蒙特卡羅方法進行計算，直接分析使用年限內(nèi)的累積失效概率，計算過程十分復雜。姚繼濤提出的時段分析法［16］不同于蒙特卡羅方法或改進蒙特卡羅方法，但計算過程同樣十分復雜，直接用于工程計算尚有不少難度。

（3）不考慮抗力退化，且荷載采用相等時段的平穩(wěn)隨機過程模型時，結(jié)構(gòu)在各時段內(nèi)的失效概率和可靠度相等［16］。在此條件下，將結(jié)構(gòu)構(gòu)件的設(shè)計使用年限或評估使用年限T分成m個相等時段，每段時長為τ=T∕m，而結(jié)構(gòu)構(gòu)件在時長T內(nèi)可靠的前提是各時段τ內(nèi)均可靠，因此有

式中：Ps（T）為結(jié)構(gòu)構(gòu)件在時長T內(nèi)的可靠度；Ps，i（τ）為結(jié)構(gòu)構(gòu)件在第i個時段τ內(nèi)的可靠度。

式（10a）又可表示為

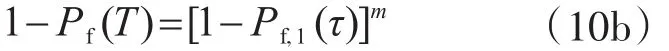
式中：Pf（T）為結(jié)構(gòu)構(gòu)件在時長T內(nèi)的累積失效概率；Ps，1（τ）為結(jié)構(gòu)構(gòu)件在第1個時段τ內(nèi)的失效概率。

當Ps，1（τ）為微小量時，式（10a）變?yōu)?/p>

即

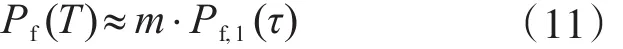
由式（10a）可知，結(jié)構(gòu)構(gòu)件在設(shè)計使用年限或評估使用年限內(nèi)的可靠度是各時段內(nèi)可靠度的乘積。由式（11）可知，設(shè)計使用年限或評估使用年限內(nèi)的累積失效概率是各時段內(nèi)失效概率之和；當各時段的失效概率相等時，累積失效概率與服役年數(shù)成正比。文獻［10］和文獻［12］也揭示了這個規(guī)律。根據(jù)這個結(jié)論，當評估使用年限比原設(shè)計使用年限縮短時，可直接對累積失效概率進行線性折減計算抗力需求折減系數(shù)，以此代替現(xiàn)行標準［17］中的可變荷載效應(yīng)折減。更重要的是，采用這種代替后，可靠度計算時僅需考慮抗力退化的影響，使計算大為簡化。

（4）當抗力隨機過程采用式（1）所示簡單模型時，可進一步將抗力隨機過程簡化為隨機變量：該隨機變量的平均值等于隨機過程R（t）的起始點隨機變量R0的平均值乘以設(shè)計使用年限或評估使用年限內(nèi)抗力衰減系數(shù)的平均值，則這個平均值相當于抗力隨機過程在空間和時間上的綜合平均值。這樣，采用全隨機過程模型的時變可靠度分析就退化為采用隨機變量模型的可靠度分析，可使分析過程得到大幅度簡化。

貢金鑫和趙國藩［14］的結(jié)構(gòu)動態(tài)可靠度分析功能函數(shù)式（9）可進一步近似表達為

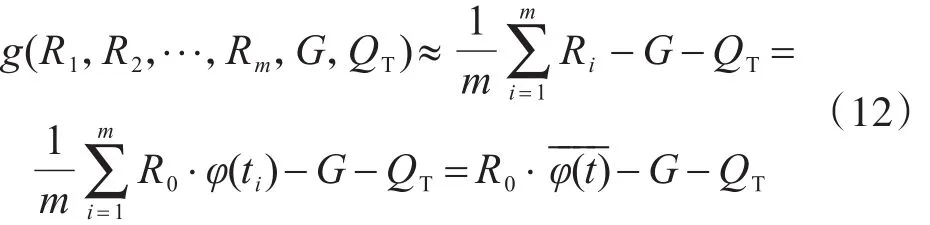
式（12）表明，貢金鑫、趙國藩［14］模型也揭示了作者提出的時變可靠度實用分析方法的前景。

2 基于設(shè)計或評估使用年限的結(jié)構(gòu)時變可靠度實用分析模型

本文在總結(jié)分析國內(nèi)外關(guān)于結(jié)構(gòu)時變可靠度研究成果的基礎(chǔ)上，建立基于評估使用年限的結(jié)構(gòu)時變可靠度實用分析模型。基本假定如下：①可變荷載采用等時段的平穩(wěn)二項矩形波模型；②既有結(jié)構(gòu)的評估使用年限不超過設(shè)計使用年限；③結(jié)構(gòu)構(gòu)件最短的評估使用年限為5年，與我國統(tǒng)一標準［1-2］規(guī)定的臨時結(jié)構(gòu)的設(shè)計使用年限相當；④抗力隨機過程可用式（1）所示服役起始點隨機變量乘以一個確定的抗力衰減函數(shù)表示。

2.1 用累積失效概率表達的可靠度條件方程

不考慮抗力退化時，設(shè)結(jié)構(gòu)在設(shè)計使用年限T0內(nèi)的累積失效概率為Pf（T0），允許累積失效概率為［Pf（T0）］，則可靠度設(shè)計的條件方程為

考慮抗力退化時，式（13）變?yōu)?/p>

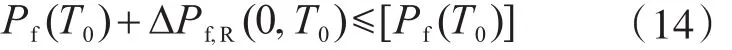
式中，ΔPf，R(0，T0)為結(jié)構(gòu)在設(shè)計使用年限 T0內(nèi)因抗力退化引起的累積失效概率增大值。

由式（14）可知，由于抗力退化，結(jié)構(gòu)在設(shè)計使用年限內(nèi)的累積失效概率增大，可能導致結(jié)構(gòu)的可靠度達不到目標可靠度要求。

當進一步考慮設(shè)計使用年限縮短時，式（14）變?yōu)?/p>

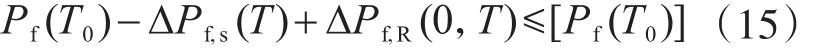
式中：T為縮短后的設(shè)計使用年限；ΔPf，s(T)為設(shè)計使用年限縮短引起的累積失效概率降低值（其實質(zhì)是荷載效應(yīng)減小引起）；ΔPf，R(0，T)為結(jié)構(gòu)在設(shè)計使用年限T內(nèi)因抗力退化引起的累積失效概率增大值。

為便于理解與應(yīng)用，式（15）可表示為

式中，Pf（T）為不考慮抗力退化時，結(jié)構(gòu)在設(shè)計使用年限T內(nèi)的累積失效概率。

中美雙方的報道在包容資源的實現(xiàn)方式上頗為類似，情態(tài)動詞的使用頻率均遠遠超過其他表達方式，其中“will”頻率最高，例如：

可見，由于抗力退化，結(jié)構(gòu)的累積失效概率增大，但當設(shè)計使用年限縮短時，由于荷載效應(yīng)降低，結(jié)構(gòu)的累積失效概率又有所降低；同時考慮這兩個因素后，如滿足式（16），則結(jié)構(gòu)的實際可靠度仍能達到目標可靠度要求。

即若原設(shè)計抗力無任何富裕量（累積失效概率等于允許累積失效概率），則當抗力退化引起的累積失效概率增大值不超過設(shè)計使用年限縮短引起的累積失效概率減小值時，結(jié)構(gòu)的實際可靠度仍達到目標可靠度要求。

既有結(jié)構(gòu)評定時，必須同時考慮抗力退化和評估使用年限縮短，如評定時結(jié)構(gòu)服役年數(shù)為t0，評估使用年限為T'，則式（15）變?yōu)?/p>

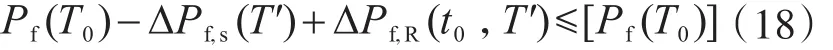
式（16）變?yōu)?/p>

式（17）變?yōu)?/p>

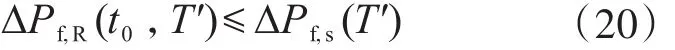
各參數(shù)的含義同新建結(jié)構(gòu)設(shè)計，但設(shè)計使用年限T應(yīng)改為評估使用年限T'。

2.2 用可靠指標表達的可靠度條件方程

用可靠指標表示時，對原設(shè)計，式（13）可表達為

考慮抗力退化時，式（14）可表達為

式中，ΔβR(0，T0)為設(shè)計使用年限T0內(nèi)因抗力退化引起實際可靠指標減小值。

考慮抗力退化和設(shè)計使用年限縮短時，式（15）可表達為

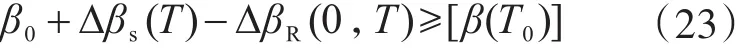
式（16）可表達為

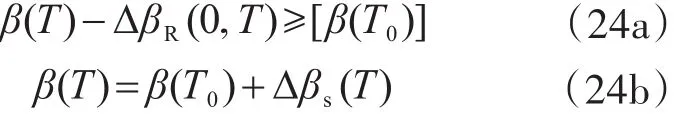
式中：Δβs（T）為設(shè)計使用年限由T0縮短為T引起的實際可靠指標增大值（其實質(zhì)是荷載效應(yīng)減小引起）；ΔβR(0，T)為設(shè)計使用年限T內(nèi)因抗力退化引起實際可靠指標減小值；β（T）為不考慮抗力退化時，結(jié)構(gòu)在設(shè)計使用年限T內(nèi)的實際可靠指標。

當β0=[β(T0)]時，式（23）退化為

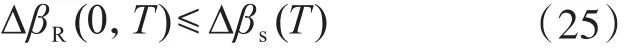
即若原設(shè)計抗力無任何富裕量（實際可靠指標等于目標可靠指標），則當抗力退化引起的實際可靠指標降低值不超過設(shè)計使用年限縮短引起的實際可靠指標增大值時，結(jié)構(gòu)的實際可靠度仍達到目標可靠度要求。

對既有結(jié)構(gòu)評定，式（23）變?yōu)?/p>

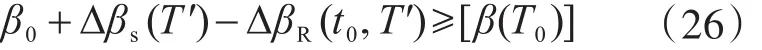
式（24）變?yōu)?/p>

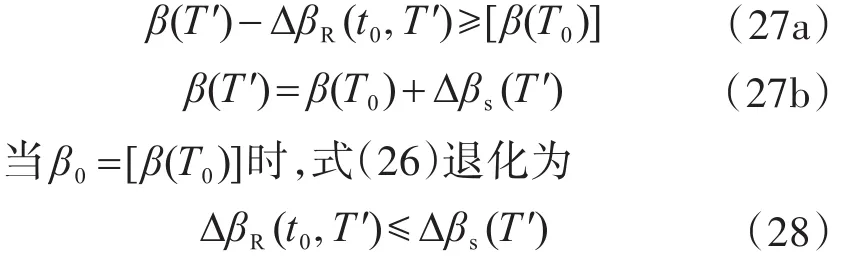
2.3 用抗力-需求比表達的可靠度條件方程

因直接采用可靠指標評定既有結(jié)構(gòu)可靠性很不方便，工程實踐中一般用抗力-荷載效應(yīng)比R∕（γ0S）來評定既有結(jié)構(gòu)可靠性。荷載效應(yīng)實質(zhì)上也是抗力需求，故抗力-荷載效應(yīng)比實質(zhì)上也是抗力-抗力需求比。由以下的分析可知，設(shè)計或評估使用年限縮短時，用抗力需求折減代替荷載效應(yīng)折減描述更為貼切。

當結(jié)構(gòu)重要性系數(shù)γ0=1.0時，式（21）和式（22）分別用抗力-需求比的形式表達為

式中，R（t）和S（T）分別為抗力和荷載效應(yīng)函數(shù)；φR(T0|0)為設(shè)計使用年限內(nèi)的抗力平均退化系數(shù)，其值等于時段（0，T0）內(nèi)抗力衰減函數(shù)φ（t）的平均值，可用下式計算：

式（23）、式（24）可表達為

式中，λR（T）為設(shè)計使用年限縮短引起的抗力需求折減系數(shù)。

當R(0)=S(T0)時，式（31）退化為

即若原設(shè)計抗力無任何富裕量（服役起始點抗力等于荷載效應(yīng)），則當設(shè)計使用年限內(nèi)的抗力平均退化系數(shù)不低于設(shè)計使用年限縮短引起的抗力需求折減系數(shù)時，結(jié)構(gòu)的可靠度仍達到原設(shè)計水平。

既有結(jié)構(gòu)評定時，式（31）變?yōu)?/p>

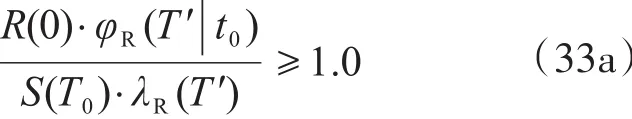
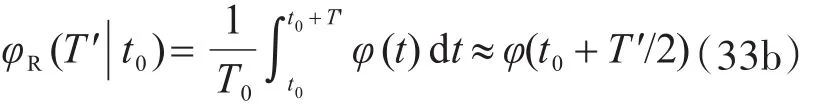
既有結(jié)構(gòu)評定時，應(yīng)采用評定時的抗力R（t0）代替服役起始點抗力R（0）進行結(jié)構(gòu)驗算，故式（33）可表達為

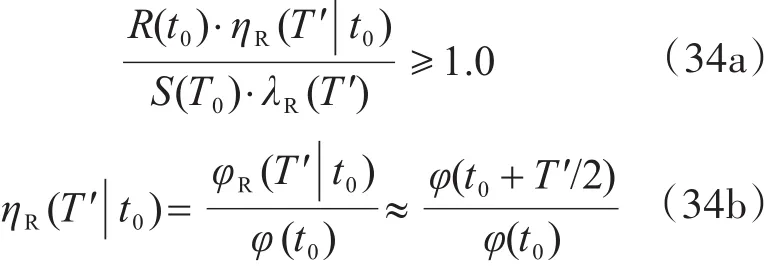
式中，ηR(T′|t0)為抗力平均退化系數(shù)，其值等于評估使用年限內(nèi)的抗力平均值與評定時的抗力之比值。

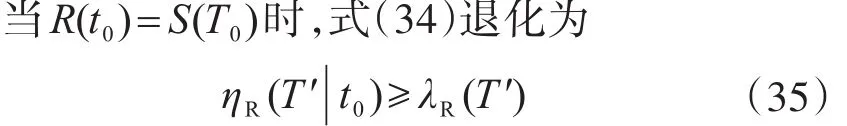
即若評定時結(jié)構(gòu)抗力無任何富裕量（評定時的抗力等于設(shè)計使用年限內(nèi)的荷載效應(yīng)），則當評估使用年限內(nèi)的抗力平均退化系數(shù)不小于評估使用年限縮短引起的抗力需求折減系數(shù)時，結(jié)構(gòu)的可靠度仍達到評定時的水平。

3 不同設(shè)計或評估使用年限下的抗力需求折減系數(shù)分析與取值建議

當抗力R和荷載效應(yīng)S均為正態(tài)分布時，結(jié)構(gòu)的可靠指標為

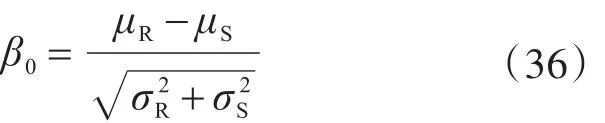
式中：μR和μS分別抗力和荷載效應(yīng)的平均值；σR和σS分別抗力和荷載效應(yīng)的標準差。

為給出荷載效應(yīng)折減系數(shù)λS（T）的近似建議值，假定設(shè)計或評估使用年限縮短為T時，荷載效應(yīng)的平均值減小為μS（T）而標準差保持不變，則結(jié)構(gòu)實際可靠指標β（T）為

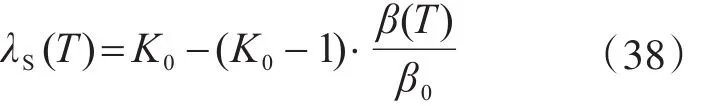
式中，λS(T)為評估使用年限縮短時的荷載效應(yīng)折減系數(shù)。

由式（37）可知，當評估使用年限縮短時，由于荷載效應(yīng)降低，結(jié)構(gòu)實際可靠指標增大。而根據(jù)不同評估使用年限內(nèi)的允許累積失效概率及其目標可靠指標相等的原則，此時的目標可靠指標仍取為β0，則可對抗力需求進行折減：

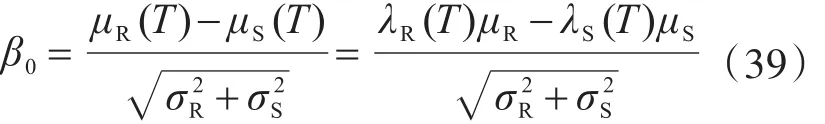
則由式（36）、式（38）和式（39）可得：

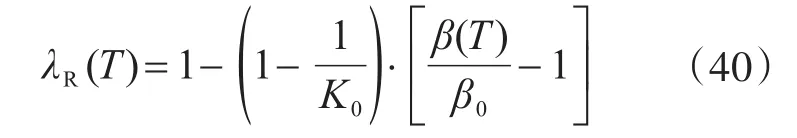
我國統(tǒng)一標準［1-2］規(guī)定，一般建筑結(jié)構(gòu)的安全等級為二級，其設(shè)計使用年限為50年，其目標可靠指標對延性破壞構(gòu)件和脆性破壞構(gòu)件分別為3.2和3.7。安全系數(shù)可根據(jù)下式計算：

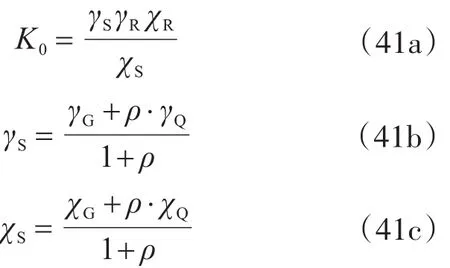
式中，γR和χR分別為抗力分項系數(shù)和均值系數(shù)，15類構(gòu)件的取值見文獻［18］；γS和χS分別為總荷載效應(yīng)的分項系數(shù)和均值系數(shù)；ρ為可變荷載與永久荷載標準值之比（取值在0.1～2），γG和γQ分別為永久荷載和可變荷載的分項系數(shù)（根據(jù)文獻［2］分別取1.3和1.5）；χG和χQ分別為永久荷載和可變荷載的均值系數(shù)，取值見文獻［18］。

根據(jù)上述條件計算得到延性破壞和脆性破壞兩類構(gòu)件的安全系數(shù)K0最小值、最大值及平均值，見表1。

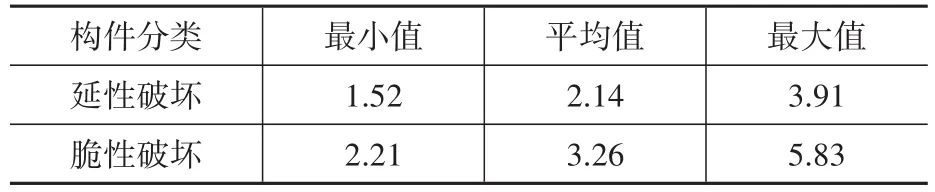
表1 安全系數(shù)K0取值的計算結(jié)果Table 1 Calculation results of safety factor K0

根據(jù)上述條件，設(shè)最小評估使用年限為5年（與臨時結(jié)構(gòu)的設(shè)計使用年限相同），將設(shè)計使用年限分為10個相等時段，每個時段為5年，則根據(jù)等時段內(nèi)結(jié)構(gòu)失效概率相等的原則，可計算不同設(shè)計或評估使用年限下的累積失效概率Pf（T）及其對應(yīng)的可靠指標β（T），再按式（40）計算λR（T），計算結(jié)果見表2。可見，延性破壞構(gòu)件的β（T）∕β0略大于脆性破壞構(gòu)件；由于破壞類型和K0的不同，各類構(gòu)件的λR（T）計算值有一定差異，其中以K0最小時的延性破壞構(gòu)件的λR（T）計算值最大。為工程應(yīng)用方便，建議將各類構(gòu)件的λR（T）統(tǒng)一取值，其建議值列于表2中。可見，該建議值大致相當于K0取平均值時的計算值；對K0較大的構(gòu)件取值略偏高（略偏安全），對K0較小的構(gòu)件取值略偏低（略偏不安全）。但以上分析結(jié)果是根據(jù)“抗力和荷載效應(yīng)均為正態(tài)分布”等假定得出的；當采用更精細的分析方法時得到的λR（T）取值會更低，因此本文的λR（T）建議取值不會偏不安全，作者將另文分析。對于設(shè)計使用年限為5年的臨時結(jié)構(gòu)，其λR（T）建議值為0.9，與我國《建筑結(jié)構(gòu)可靠度設(shè)計統(tǒng)一標準》（GB 50068—2001）［19］對該類結(jié)構(gòu)的重要性系數(shù)γ0取值相同。

我國《建筑結(jié)構(gòu)荷載規(guī)范》（GB 50009—2012）［17］第 3.2.5條的條文說明指出，確定可變荷載設(shè)計使用年限調(diào)整系數(shù)γL可采用兩種方法：一是使結(jié)構(gòu)在設(shè)計使用年限內(nèi)的可靠指標與在設(shè)計基準期的可靠指標相等；二是使可變荷載按設(shè)計使用年限定義的標準值與按設(shè)計基準期定義的標準值具有相同的概率分位值。文獻［17］是按第二種方法確定γL。本文建議的λR（T）實質(zhì)上是按第一種方法確定的γL。從上述分析可知，如對設(shè)計或評估使用年限為5年的結(jié)構(gòu)重要性系數(shù)γ0取為0.9后，不應(yīng)再對可變荷載進行折減。

4 結(jié)論

本文在分析國內(nèi)外關(guān)于考慮抗力和荷載效應(yīng)時變性的結(jié)構(gòu)可靠度研究成果的基礎(chǔ)上，提出了既有結(jié)構(gòu)基于評估使用年限的可靠度評定實用方法。研究得到如下結(jié)論：

（1）不考慮抗力退化，且荷載采用相等時段的平穩(wěn)隨機過程模型時，結(jié)構(gòu)在各時段內(nèi)的失效概率和可靠指標相等。設(shè)計或評估使用年限內(nèi)的可靠度是各時段內(nèi)可靠度的乘積，即設(shè)計使用年限或評估使用年限內(nèi)的累積失效概率是各時段內(nèi)失效概率之和。由此可得到“結(jié)構(gòu)的累積失效概率與服役年數(shù)成正比”的規(guī)律。當設(shè)計或評估使用年限縮短時，可對累積失效概率進行線性折減確定抗力需求折減系數(shù)。

（2）結(jié)構(gòu)抗力隨機過程模型采用起始點隨機變量乘以一個確定的抗力衰減函數(shù)表示，則結(jié)構(gòu)抗力隨機過程可退化為隨機變量，其抗力平均值等于服役起始點抗力隨機變量的平均值乘以結(jié)構(gòu)在使用或評估年限內(nèi)的抗力平均退化系數(shù)。采用全隨機過程模型的時變可靠度分析由此可退化為采用隨機變量模型的可靠度分析，可使分析過程得到大幅度簡化。

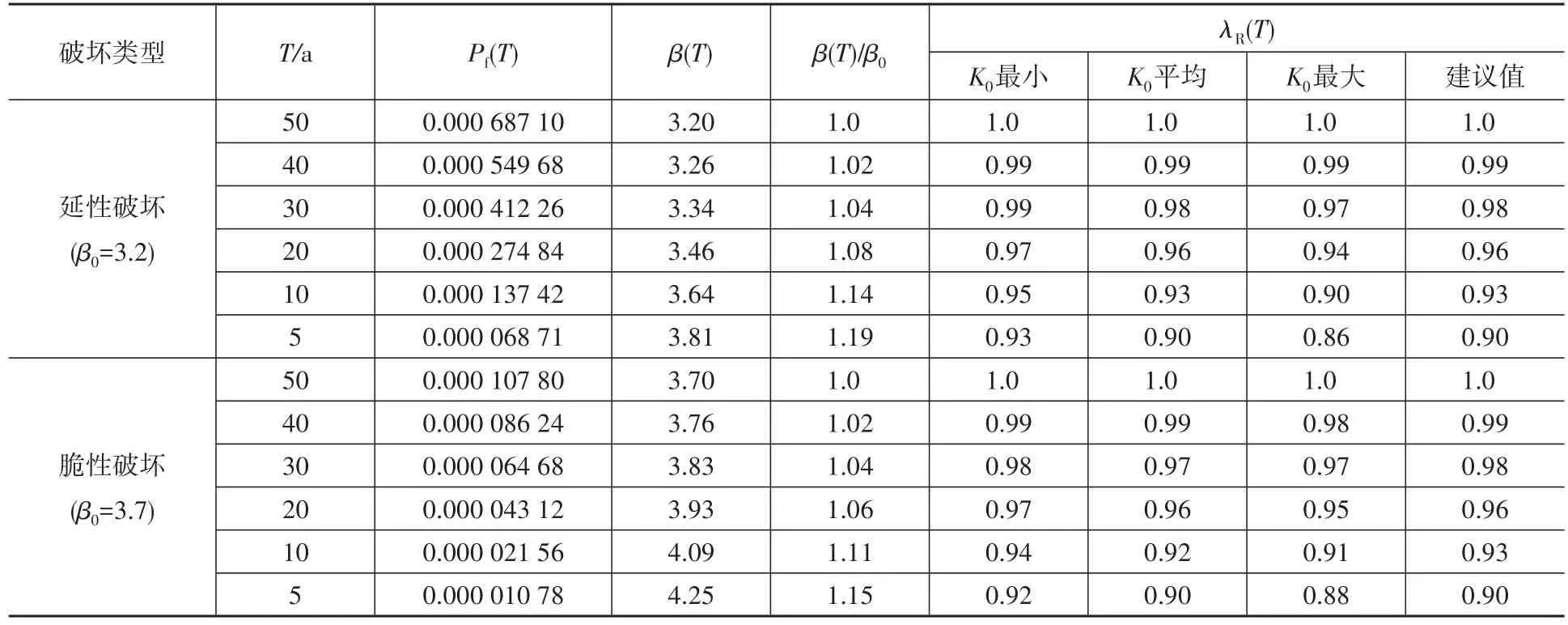
表2 不同設(shè)計或評估使用年限下的λR（T）取值Table 2 Value of λR（T）under different design or assessed working lives

（3）本文同時考慮結(jié)構(gòu)在評估使用年限內(nèi)的抗力退化和評估使用年限縮短引起的抗力需求折減，建立了既有結(jié)構(gòu)基于評估使用年限的累積失效概率和可靠指標條件方程。為便于工程應(yīng)用，用抗力平均退化系數(shù)和抗力需求折減系數(shù)表示可靠指標的動態(tài)變化，建立了既有結(jié)構(gòu)評定的抗力-需求比實用表達式。

（4）本文提出的不同評估使用年限下的抗力需求折減系數(shù)，是使結(jié)構(gòu)在評估使用年限內(nèi)的目標可靠指標與在設(shè)計基準期的目標可靠指標相等的原則下得到的，可代替《建筑結(jié)構(gòu)荷載規(guī)范》（GB 50009—2012）［17］中的可變荷載的設(shè)計使用年限調(diào)整系數(shù)，其建議值與《建筑結(jié)構(gòu)可靠度設(shè)計統(tǒng)一標準》（GB 50068—2001）［2］中的結(jié)構(gòu)重要性系數(shù)有效銜接。