基于CMIP5模式與Argo觀測數據的海洋有效重力勢能分析

牛凡，王濤,2，廖光洪,2*

( 1. 河海大學 海洋學院，江蘇 南京 210098；2. 青島海洋科學與技術試點國家實驗室 區(qū)域海洋動力學與數值模擬功能實驗室，山東 青島 266237)

1 引言

第五次國際耦合模式比較計劃（CMIP5）由世界氣候研究計劃（WCRP）組織實施[1]，該計劃在CMIP3的基礎上做了很大改進，并建立了新的排放情景—典型濃度路徑（RCPs）[2]，參與該計劃的50多個模式的模擬結果已被IPCC AR5采用[3]。但在氣候模擬過程中，不同的初始條件、邊界條件、情景、觀測、模型參數等都會使模式的模擬結果存在很大程度的不確定性，因此，評估模式的模擬能力就顯得尤為重要[4-7]。過去人們主要從溫度、降水、風速以及碳循環(huán)等氣候變量對CMIP5模式進行評估[7-8]。而能量是氣候系統(tǒng)內各類物理過程、生命活動以及各圈層間相互作用的原動力，因此從能量的角度來評估CMIP5模式是十分有意義的。

研究各種不同形式能量之間的轉化關系，一直是海洋動力學研究的重要課題[9]。對于不可壓海洋來說，海水在調整過程中體積保持不變，外部壓力不做功，無彈性勢能，因此其勢能為重力勢能（Gravitational Potential Energy，GPE）。重力場是大尺度環(huán)流的背景場，重力勢能的收支平衡在海洋環(huán)流中具有十分重要的作用。海洋環(huán)流發(fā)生在地球自轉的重力場環(huán)境中，當速度場不符合地轉平衡時，海洋會調整速度場使其趨于地轉平衡，與此同時部分動能會轉化為勢能，而當密度場不平衡時海洋亦會驅動地轉流使其平衡，此時部分重力勢能則轉化為動能[10]。

海洋中蘊藏著巨大的重力勢能，Oort等[9]以水深3 750 m為參考面計算得到的全球海洋重力勢能量值大約為。盡管全球海洋的重力勢能很大，但其中大部分不能轉化為動能，也不能參與海洋中的能量循環(huán)[11]，有效重力勢能（Available Gravitational Potential Energy，AGPE）是其中能夠轉化為動能的一小部分重力勢能。有效重力勢能定義為物理態(tài)海洋經過絕熱調整到參考態(tài)時釋放的能量，即重力勢能與參考重力勢能（Reference Gravity Potential Energy，RGPE）之差。其中，物理態(tài)指現實海洋所呈現的狀態(tài)，參考態(tài)則是指系統(tǒng)處于最小重力勢能時的狀態(tài)，理論上只有當密度面完全水平，水體上輕下重時重力勢能達到最小。根據有效重力勢能的定義，只要海水在水平方向存在密度差或在垂向上存在不穩(wěn)定層結，就存在有效重力勢能。海洋有效重力勢能的概念一直存在爭議[11]，早期科學家利用相對更容易求得的物理量來近似估算有效重力勢能，比如Bray和Fofonoff[12]引入Sandst?rm和Helland-Hansen[13]所提出的動力高度（）的概念來計算有效重力勢能。其后，Huang[14]指出Oort等[9,15]提出的基于準地轉近似計算有效重力勢能的方法因為沒有考慮層結如何維持而存在巨大缺陷。

在計算有效重力勢能時，最常用的做法是從確定最小勢能的參考態(tài)入手，目前主要存在4種有效重力勢能參考狀態(tài)的定義方法：（1）采用每層水體的密度平均作為參考狀態(tài)[16-18]；（2）采用特定密度剖面作為參考態(tài)[19]；（3）將參考態(tài)定義為中性浮力面（Level of Neutral Buoyancy，LNB）[20-21]，它表示物理狀態(tài)的海水絕熱調整到最小勢能狀態(tài)，Huang[22]在其基礎上提出了迭代法；（4）概率密度函數法[23-24]。其中，采用作為參考狀態(tài)方法的優(yōu)點是方便計算，缺點是沒有區(qū)分有效重力勢能和有效勢能。Feng等[25]在其基礎上證明該方法適用于計算中尺度范圍的有效重力勢能。而迭代法則更適用于估算真實大洋有效重力勢能，但其計算量大且忽略了海盆地形對水體調整的影響。

本文利用全球海洋Argo網格數據集和CMIP5中9個模式輸出結果，采用方法（1）計算了中尺度有效重力勢能（Mesoscale Eddy Available Gravity Potential Energy，EAGPE），用方法（3）計算了海盆積分的有效重力勢能。對計算結果進行了比較分析研究。

2 數據及方法

2.1 數據介紹

實測數據采用全球海洋Argo網格數據集（簡稱“BOA_Argo”）。BOA_Argo是由簡單有效的逐步訂正法與混合層模型相結合得到的，包含溫度、鹽度、等溫層深度、混合層深度等變量。時間范圍為2006年1月至2017年12月；時間分辨率為逐月；空間范圍為全球海洋80°S～80°N，環(huán)全球經度；水平空間分辨率為 1°×1°。

模式數據選取CMIP5中的未來預估模擬實驗高濃度路徑RCP8.5下的9個模式（2006年1月至2017年12月）以及其中4個模式的歷史模擬結果（1980年1月至2005年12月），9個模式的網格分辨率和所采用的垂向混合方案見表1。

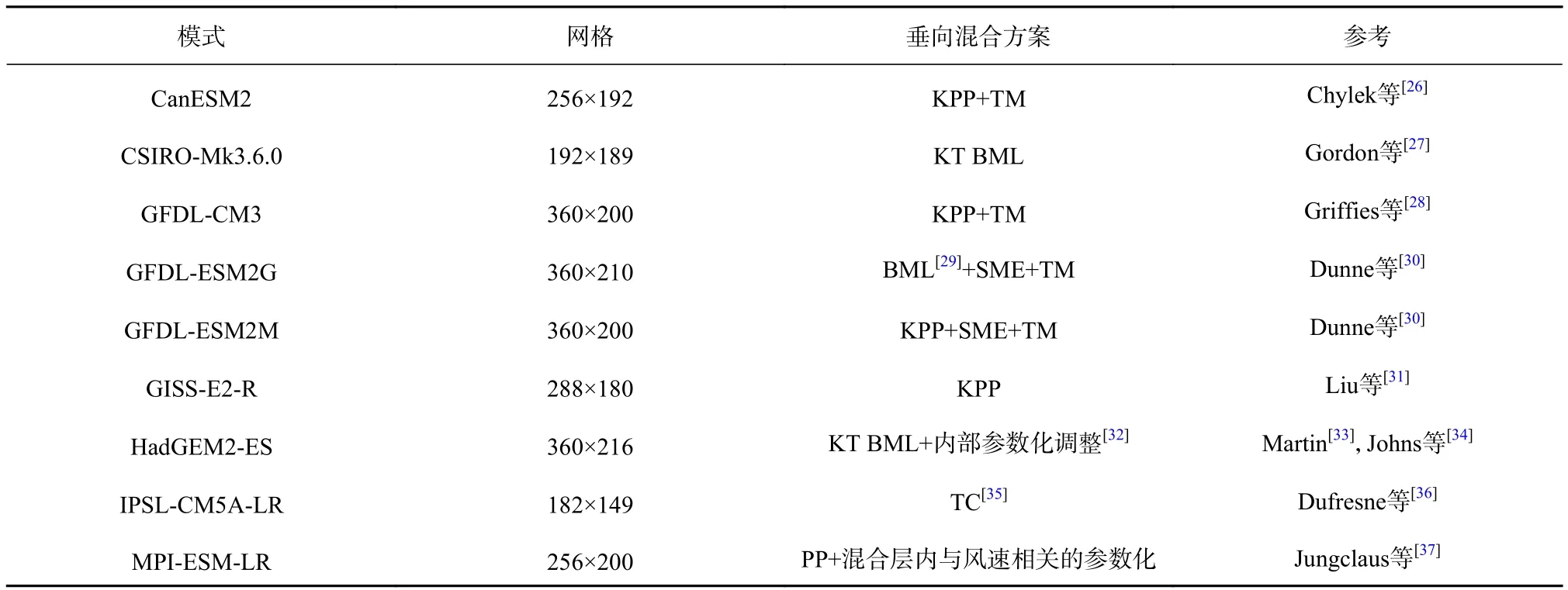
表1 模式介紹Table 1 Models introduction

2.2 計算方法

2.2.1 海盆尺度有效重力勢能計算

由于海水狀態(tài)方程復雜的非線性使得海盆尺度參考態(tài)確定起來十分困難，人們曾試圖利用解析法解決這一問題[42-43]，但至今參考態(tài)仍無法明確表示。Huang[22]從經典有效勢能定義出發(fā)，以重力勢能最小值狀態(tài)做參考態(tài)，提出一種“迭代法”的程序算法解決了這一問題。由于Argo數據垂向深度為2 000 m，本文借鑒該方法，在體積守恒的前提下計算全球大洋2 000 m以上水體有效重力勢能。其步驟如下（圖1）：

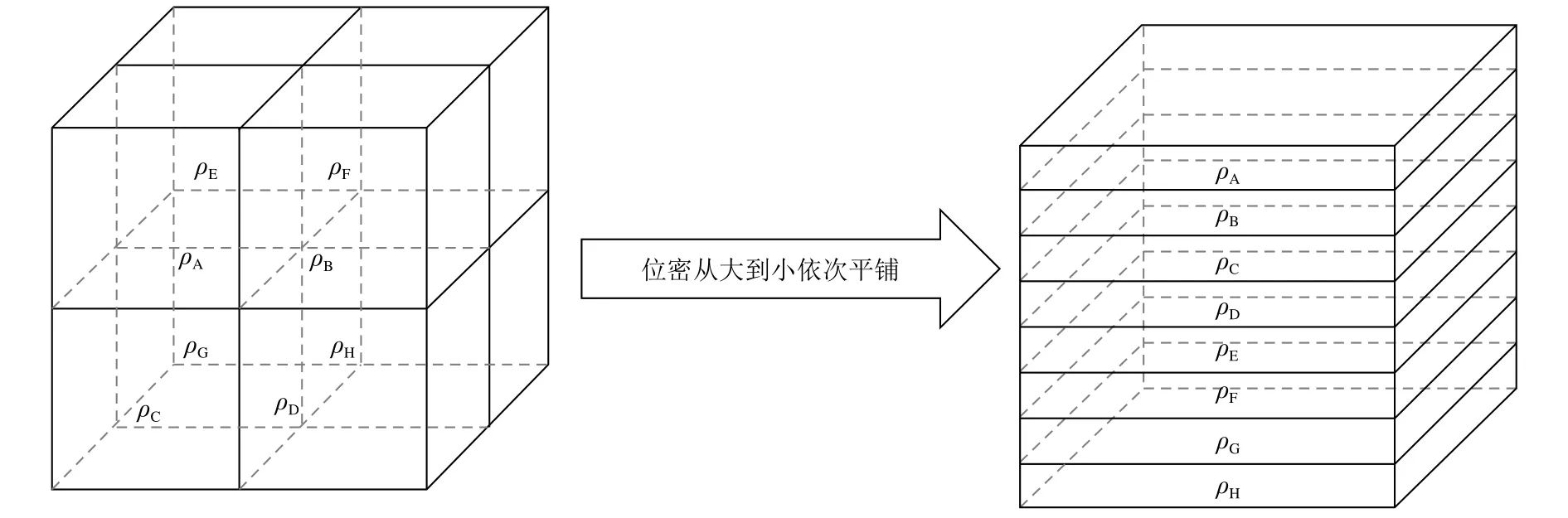
圖1 “迭代法”中計算三維海水參考勢能圖示Fig. 1 A brief description of three dimensional seawater iteration method for calculating reference gravity potential energy

（1）將模式數據插值到Argo數據網格上，對所有數據有效網格求交集，以便定量分析模式和實測數據的有效重力勢能，真實網格地形即為一個階梯碗狀海盆。

（2）首先計算2 000 m以上所有網格的水體單元在2 000 m深處的參考壓強下的位勢密度，將位密序列從最重的水體單元按體積守恒從階梯碗狀底部開始平鋪，每個水體單元鋪疊厚度為這里M，分別是水體單元的質量和密度，S（k）為最底層階梯狀海盆面積。在平鋪的過程中，要注意兩點：①如果鋪蓋厚度超過階梯碗狀海盆該層厚度，則要改變S（k）為S（k-1）；②當最后一個水體單元平鋪后，該層總厚度大于該層階梯高度，將該層底部深度（即2 000 m）減去該層總厚度作為新一層參考壓強，并對剩下的所有水體在新的參考壓強下重新計算位勢密度。

（3）之前排列好的水體固定，剩下的水體在步驟（2）的基礎上繼續(xù)鋪疊，直到該層再次鋪疊完成，并重復步驟（2）、（3），直至所有水體排序完畢。

2.2.2 準地轉框架下中尺度有效重力勢能計算

Pedlosky[16]，Wright[17]和 Oort等[9,15]用類似Lorenz[18]的辦法提出準地轉框架下的有效重力勢能定義，雖然不適用于全球尺度的有效重力勢能的計算[22]，但已被證明適用于計算中尺度范圍的有效重力勢能[24]。隨后，Kang和Finger[44]給出了單層水體中尺度有效重力勢能的計算公式為

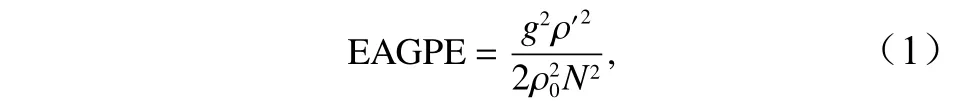
式中，N為浮力頻率水體單元的密度偏差，反映了密度隨時間變化的離散度；表示每個水體單元密度的時間平均。擾動密度被廣泛地應用于計算內波引起的深度積分[45-46]或體積積分[47-48]的有效重力勢能；其次，密度（溫度、鹽度或速度）偏差平方隨時間的變化也被認為是一個與混合率相關的重要物理量[49-51]。

本文利用單層水體EAGPE的計算公式計算出模式數據和實測數據上層200～500 m各層的EAGPE，再根據水體厚度利用加權平均計算出全球大洋上層平均的 EAGPE200～500m。

為了便于分析影響有效重力勢能的因素，對中尺度有效重力勢能計算公式進行分解

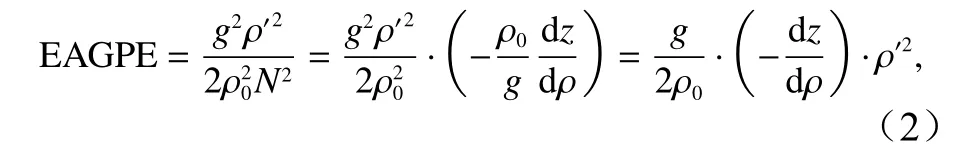
3 結果分析

3.1 全球積分的有效重力勢能

基于Argo與CMIP5中的9個模式資料，以2 000 m為參考深度，利用海盆尺度有效勢能的計算方法得到了2006-2017年間的GPE、RGPE、AGPE。基于Argo數據計算的GPE、RGPE和AGPE分別為J，可以看出AGPE占總重力勢能中非常小的一部分（0.38‰）。圖2是各模式所計算的GPE、RGPE和AGPE與Argo結果的相對誤差，用于評估各模式數值結果的模擬能力。

從圖2可以看出，9個模式的GPE和RGPE與Argo觀測數據所計算的結果相對誤差均較小，最大相對誤差小于0.06%。GFDL-ESM2G以及HadGEM2-ES這兩個模式較其他模式而言計算結果均與Argo最為接近，而GISS-E2-R模式是9個模式中計算結果與Argo觀測相差最大的。Huang等[8]在評估CMIP5模式南半球夏季南大洋混合層深度以及夏季北大西洋與北太平洋混合層深度時發(fā)現GISS-E2-R所模擬的混合層深度明顯低于觀測值。

在CMIP5模式中，不同模式采用的垂直混合方案不盡相同，而垂直湍流運動也是海洋外部能量向重力勢能轉化的重要途徑[52]，這是因為海洋中的垂直湍流混合通過改變海水溫鹽層結影響密度的變化，進而影響海洋重力勢能。通過對模式垂直混合方案進一步分析，發(fā)現GISS-E2-R模式采用了單一的KPP垂直混合方案，這種單一的混合方案不足以充分模擬海洋內部的垂向混合過程[8]。Madec等[35]的湍流閉合方案包含了波破碎、朗繆爾環(huán)流、雙擴散和潮汐驅動混合的影響，這可能是IPSL-CM5A-LR模式結果計算重力勢能偏高的原因。

為了分析海盆尺度GPE、RGPE和AGPE的時間變化特征，圖3給出了3個量的時間變化序列。由Argo觀測和模式計算的有效重力勢能均呈現出一致的年際變化特征，振幅也較為接近，特別是季節(jié)變化規(guī)律極為一致。重力勢能與參考重力勢能在每年的3、4月份達到最小（北半球春季），在9、10月份達到最大（北半球秋季）。而有效重力勢能的季節(jié)變化規(guī)律則與之相反，即在每年的3、4月份達到最大（北半球春季），而9、10月份達到最小（北半球秋季），有效重力勢能的這一季節(jié)變化特征主要是由于太陽直射點的季節(jié)變化引起的，太陽直射點的季節(jié)遷移對海水吸熱有直接影響。海水失熱導致海水增密，從而引起海水重力不穩(wěn)定性增強，繼而導致海水的有效重力勢能變大；反之，海水吸熱導致海水變輕，海水的重力不穩(wěn)定性減弱，海水的有效重力勢能下降。

將重力勢能與參考重力勢能垂向積分后相減得到海盆尺度的有效重力勢能的空間分布，如圖4所示，其空間分布呈關于赤道南北對稱結構，且中心高兩邊低的分布特征，特別是太平洋和大西洋的大洋西側均低于大洋東側。雖然海盆尺度的參考重力勢能在空間分布上僅為每個空間點所平鋪的重力勢能的垂向積分，但此處的有效重力勢能仍然具有一定的物理意義，南北極較重的海水以及北大西洋深層水形成區(qū)的海水可以視為有效重力勢能的“源”，而低緯度地區(qū)較輕的海水則可以視為有效重力勢能的“匯”。

3.2 中尺度有效重力勢能

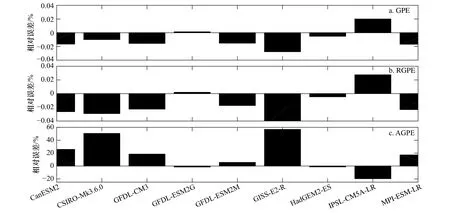
圖2 各模式計算的重力勢能（GPE）、參考重力勢能（RGPE）、有效重力勢能（AGPE）與Argo觀測結果的相對誤差Fig. 2 The relative bias of GPE, RGPE, AGPE between the model outputs and the Argo observations

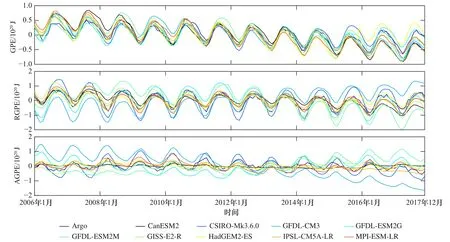
圖3 Argo觀測與各模式計算的重力勢能（GPE）、參考重力勢能（RGPE）、有效重力勢能（AGPE）時間變化序列Fig. 3 Time variations of GPE, RGPE and AGPE calculated from Argo observations and model outputs

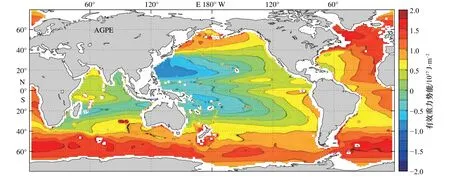
圖4 由Argo觀測計算的海盆尺度有效重力勢能（AGPE）空間分布Fig. 4 Spatial distribution of AGPE at basin scale calculated from Argo observations

海盆尺度有效重力勢能表征海盆尺度重力勢能釋放的能量上限，適用于研究有效重力勢能年際時間尺度上的演化，但其假設整個大洋的任意水體能夠自由交換，忽略了海底地形對水體絕熱調整等過程，且無法診斷海洋環(huán)流系統(tǒng)中的中尺度渦運動。中尺度有效重力勢能表征羅斯貝波變形半徑量級的水平空間尺度上能被利用的重力勢能，它可以看做海盆尺度平均流的重力勢能通過斜壓不穩(wěn)定過程釋放的能量，是中尺度渦動能重要來源[25]。

Oort等[9,15]提出的基于準地轉框架下有效重力勢能計算方法，能合理估計中尺度有效重力勢能。根據該計算方法，可以得到Argo中尺度有效重力勢能空間分布（圖5）。其分布特征顯示在強動力活躍區(qū)（黑潮、北大西洋暖流以及南極繞極流等）EAGPE十分顯著，且在太平洋以及大西洋都體現了大洋西岸的EAGPE高于大洋東岸這一分布特點。此外，北半球高值區(qū)域都處在寒暖流交匯的地方，這應是因為寒暖流交匯造成該海域重力勢能不穩(wěn)定增強，繼而影響其EAGPE。此外，對9個模式也進行中尺度有效重力勢能計算，結果如圖6所示。模式的計算結果也都體現了強對流區(qū)域EAGPE較高以及大洋西岸高于大洋東岸等分布特點，總體來看，GISS-E2-R模式在空間模擬結果上整體偏低，特別是在赤道地區(qū)；而MPIESM-LR模式結果則整體上高于Argo觀測計算結果。由CanESM2模式計算的EAGPE明顯高于Argo觀測計算結果。

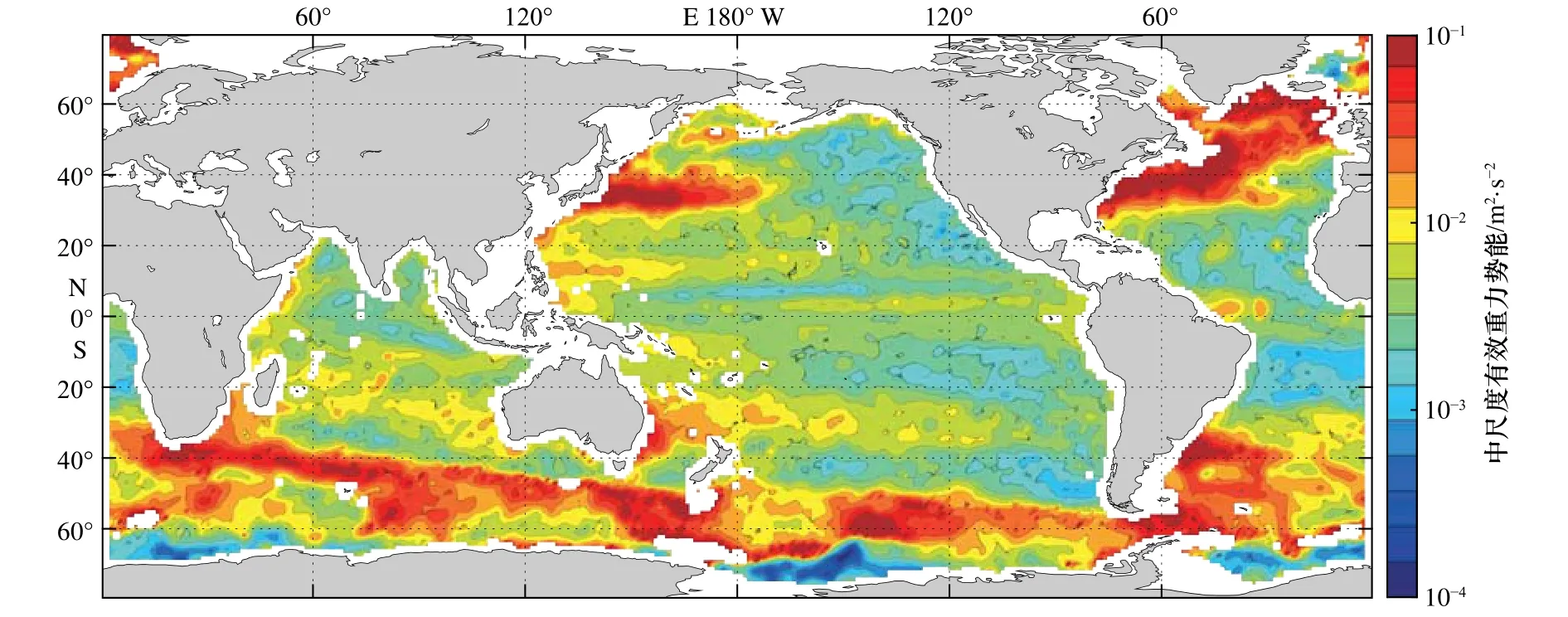
圖5 由Argo觀測計算的200～500 m深度平均的中尺度有效重力勢能（EAGPE）空間分布Fig. 5 Spatial distribution of depth-averaged EAGPE between 200 m and 500 m calculated from Argo observations

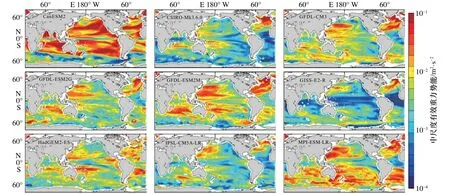
圖6 由模式計算的200～500 m深度平均的中尺度有效重力勢能（EAGPE）空間分布Fig. 6 Spatial distribution of depth-averaged EAGPE between 200 m and 500 m calculated from model outputs

擾動密度平方項空間分布與EAGPE空間分布十分相近，其值在動力活躍區(qū)域較大，這是因為在這些區(qū)域密度變化相對劇烈，但在南大洋沿岸海域模式未能很好再現較強的密度擾動變化。而密度梯度倒數項與EAGPE空間分布呈相反的分布特征，中低緯度海域的密度梯度倒數要小于高緯度海域，特別是在南大洋沿岸海域以及北大西洋暖流海域該項達到最大。對比圖7和圖8，可以看出CanESM2模式的EAGPE偏高的原因是其密度梯度較小，垂向混合偏強，從而導致密度梯度倒數較其他模式而言過大，繼而其EAGPE偏大。GISS-E2-R模式密度梯度倒數的空間分布在赤道附近相對偏低，即其密度梯度較大，致使該區(qū)域垂向混合較弱，垂向混合不足是導致GISS-E2-R模式EAGPE偏低的原因。

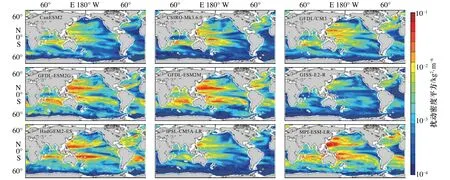
圖7 各模式擾動密度平方項的空間分布Fig. 7 Spatial distribution of the square of density perturbation in each model

圖8 各模式密度梯度倒數項的空間分布Fig. 8 Spatial distribution of the reciprocal of density gradient in each model

圖9 中尺度有效重力勢能（EAGPE）、擾動密度平方以及密度梯度倒數的空間分布Fig. 9 Spatial distribution of EAGPE, the square of density perturbation and the reciprocal of density gradient

為了盡可能消除各模式之間的差異，對所有模式所計算的EAGPE、擾動密度平方以及密度梯度倒數進行算數平均，在平均過程中，我們剔除了差別較大的CanESM2模式。對比Argo與模式集合平均在EAGPE、擾動密度平方以及密度梯度倒數這3項的空間分布（圖9），可以看出，EAGPE和擾動密度平方項兩者的模式集合平均結果空間分布基本一致；從模式結果計算的3個量的空間分布特點與Argo觀測結果基本一致。EAGPE在太平洋西側高于太平洋東側且在北大西洋灣流地區(qū)較強。Argo觀測結果顯示在南極繞極流區(qū)EAGPE較強，但模式結果并沒有很好再現這樣的分布特點。比較發(fā)現擾動密度平方項的模式集合平均結果在南極繞極流地區(qū)與Argo觀測結果相差較大，一個重要的原因是各模式混合參數化方案不完善導致混合不充分從而使EAGPE偏小。在密度梯度倒數項的空間分布圖中，模式集合平均結果同樣是在南極繞極流海域模擬較差，但是其Argo與模式的集合平均偏差結果要遠小于前兩項，所以模式在密度梯度倒數項模擬較優(yōu)。在南大洋區(qū)域，模式模擬的密度垂向梯度相對Argo較高，從而使該海域水體在垂直方向沒有發(fā)生充分混合，對南大洋密度擾動程度刻畫較弱，導致EAGPE偏低。

由于EAGPE可以轉化為渦動能，為了探究EAGPE、動能、渦動能三者之間的關系，對CMIP5中4個模式（CSIRO-Mk3.6.0、GFDL-ESM2G、GFDLESM2M、IPSL-CM5A-LR）歷史模擬結果進行計算，時間范圍為1980年1月至2005年12月。結果如圖10所示，歷史模擬結果的EAGPE、動能和渦動能高值區(qū)域仍然集中在黑潮、北大西洋以及南大洋區(qū)域，且GFDL-ESM2G與GFDL-ESM2M兩個模式有效重力勢能和動能在黑潮和北大西洋區(qū)域結果要比CSIROMk3.6.0和IPSL-CM5A-LR大很多。與EAGPE的模式結果相似，模式結果顯示渦動能在南大洋區(qū)域也偏弱。

為了分析模式渦動能和EAGPE的變化關系，首先對黑潮區(qū)域（20°～40°N，120°E～160°W），北大西洋灣流區(qū)域（30°～60°N，10°～60°W）和南大洋區(qū)域（30°～60°S）的渦動能和 EAGPE 進行區(qū)域積分；然后對其時間序列（1981-2005年）進行功率譜分析，其結果顯示在圖11至圖13中。從譜分析可以看出在3個區(qū)域，6個月（K2）周期和12個月（K1）周期均為顯著譜峰，即渦動能與EAGPE都具有比較明顯的半年和年變化周期。其中GFDL-ESM2G模式EAGPE和渦動能譜分析曲線顯示了顯著的一致性。此外渦動能與EAGPE時間序列相關性顯示（表2），黑潮和南大洋區(qū)域渦動能與EAGPE時間序列相關性要高于北大西洋灣流區(qū)域，GFDL-ESM2G與GFDL-ESM2M兩個模式所模擬的渦動能與EAGPE時間序列的相關性相對較高，特別是在南大洋區(qū)域，GFDL-ESM2M模式結果的渦動能和EAGPE顯著相關。

4 結論

本研究比較分析了Argo觀測資料和CMIP5中9個模式結果計算的重力勢能，參考重力勢能和有效重力勢能，主要結論如下：

（1）海盆積分的有效重力勢能：從Argo觀測與數值模式所計算的結果在季節(jié)變化規(guī)律方面極為一致，重力勢能與參考重力勢能在每年的3、4月份達到最小，在9、10月份達到最大；而有效重力勢能的季節(jié)變化規(guī)律則與之相反。該季節(jié)變化特征主要是由于太陽直射點的季節(jié)變化引起的。有效重力勢能空間分布呈現關于赤道南北對稱的結構，且中心高兩邊低的分布特征，特別是太平洋和大西洋的大洋西側均低于大洋東側。

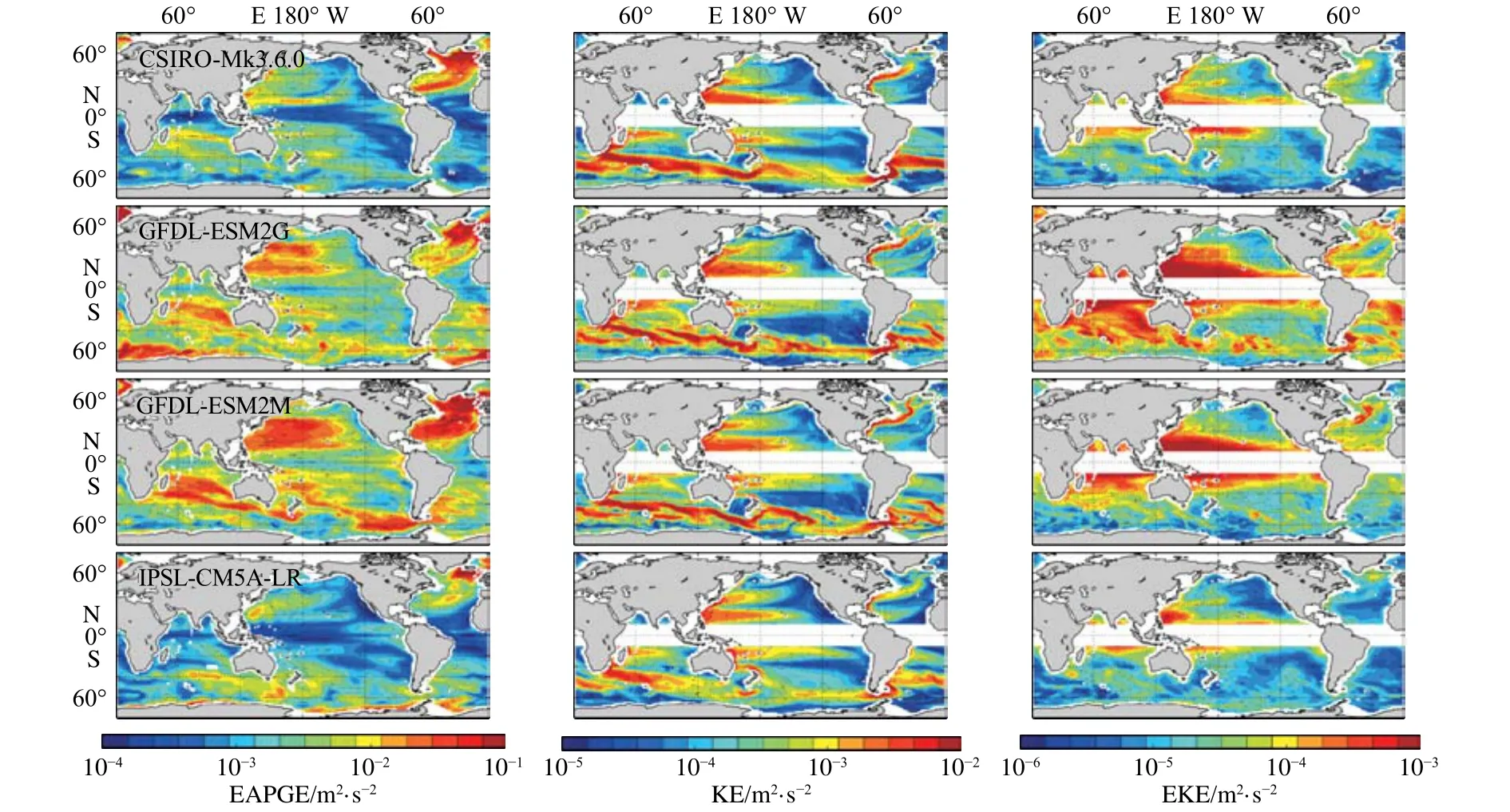
圖10 由模式計算的中尺度有效重力勢能（EAGPE）、動能（KE）、渦動能（EKE）的空間分布Fig. 10 Spatial distribution of EAGPE, KE and EKE calculated from model outputs

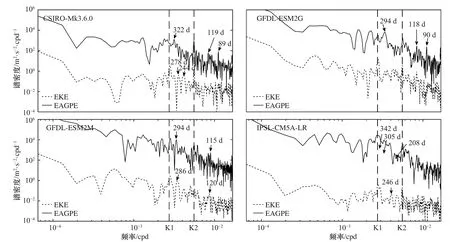
圖11 黑潮區(qū)域渦動能（EKE）與中尺度有效重力勢能（EAGPE）時間序列的功率譜Fig. 11 Power spectral of EKE and EAGPE in the Kuroshio region

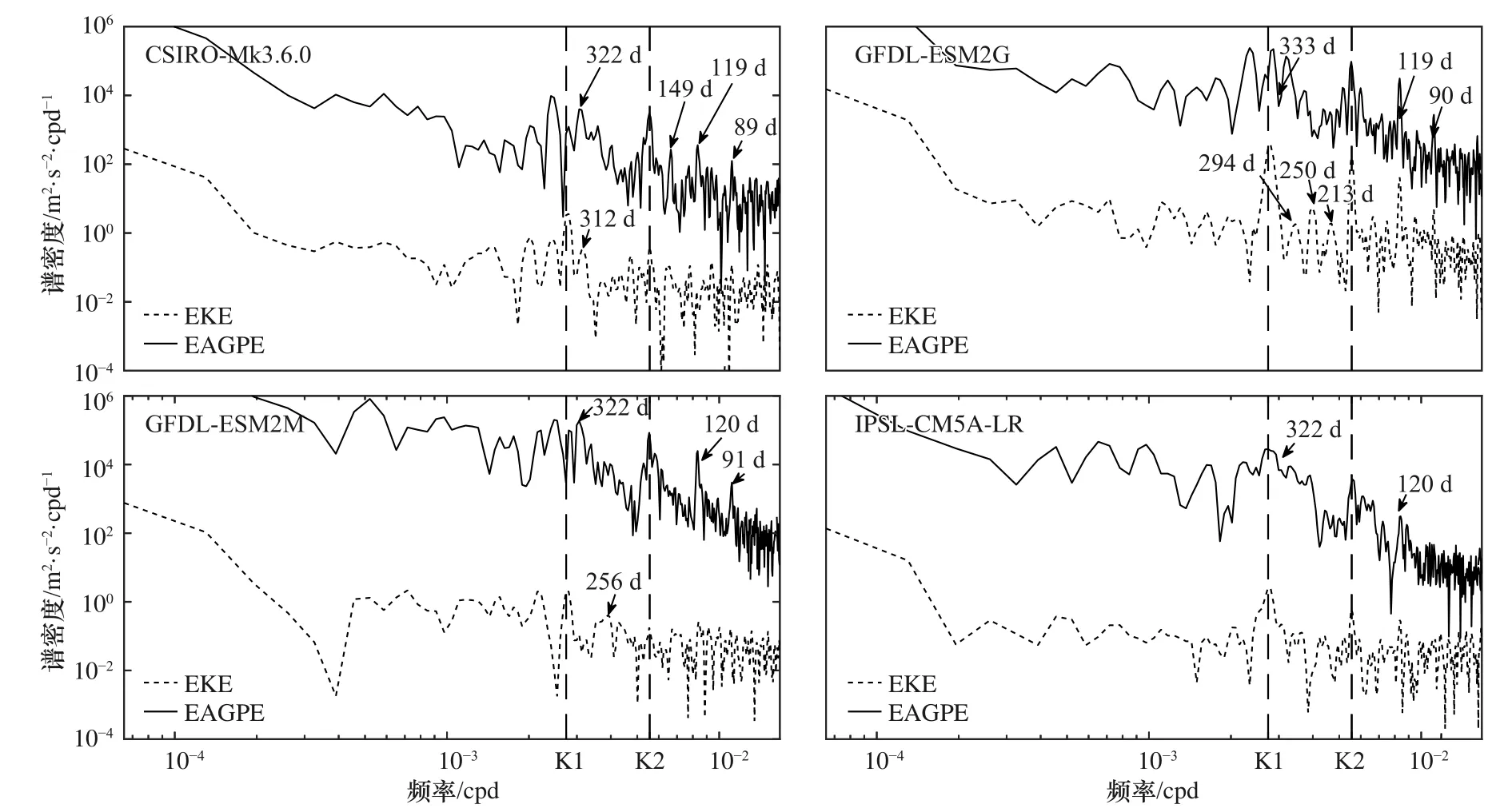
圖12 北大西洋灣流區(qū)域渦動能（EKE）與中尺度有效重力勢能（EAGPE）時間序列的功率譜Fig. 12 Power spectral of EKE and EAGPE in the gulf stream region of North Atlantic

（2）中尺度有效重力勢能和渦動能均在強流區(qū)域（黑潮、北大西洋暖流以及南極繞極流等）呈現顯著高值；在太平洋和大西洋，大洋西岸的中尺度有效重力勢能高于大洋東岸。渦動能與中尺度有效重力勢能在黑潮和南大洋區(qū)域具有較強的相關性，且具有明顯的半年和年變化周期。

（3）擾動密度平方項的空間分布與中尺度有效重力勢能空間分布特征十分相近；而密度梯度倒數項與中尺度有效重力勢能空間分布呈相反的分布態(tài)勢。擾動密度平方項對有效重力勢能的計算影響較大。

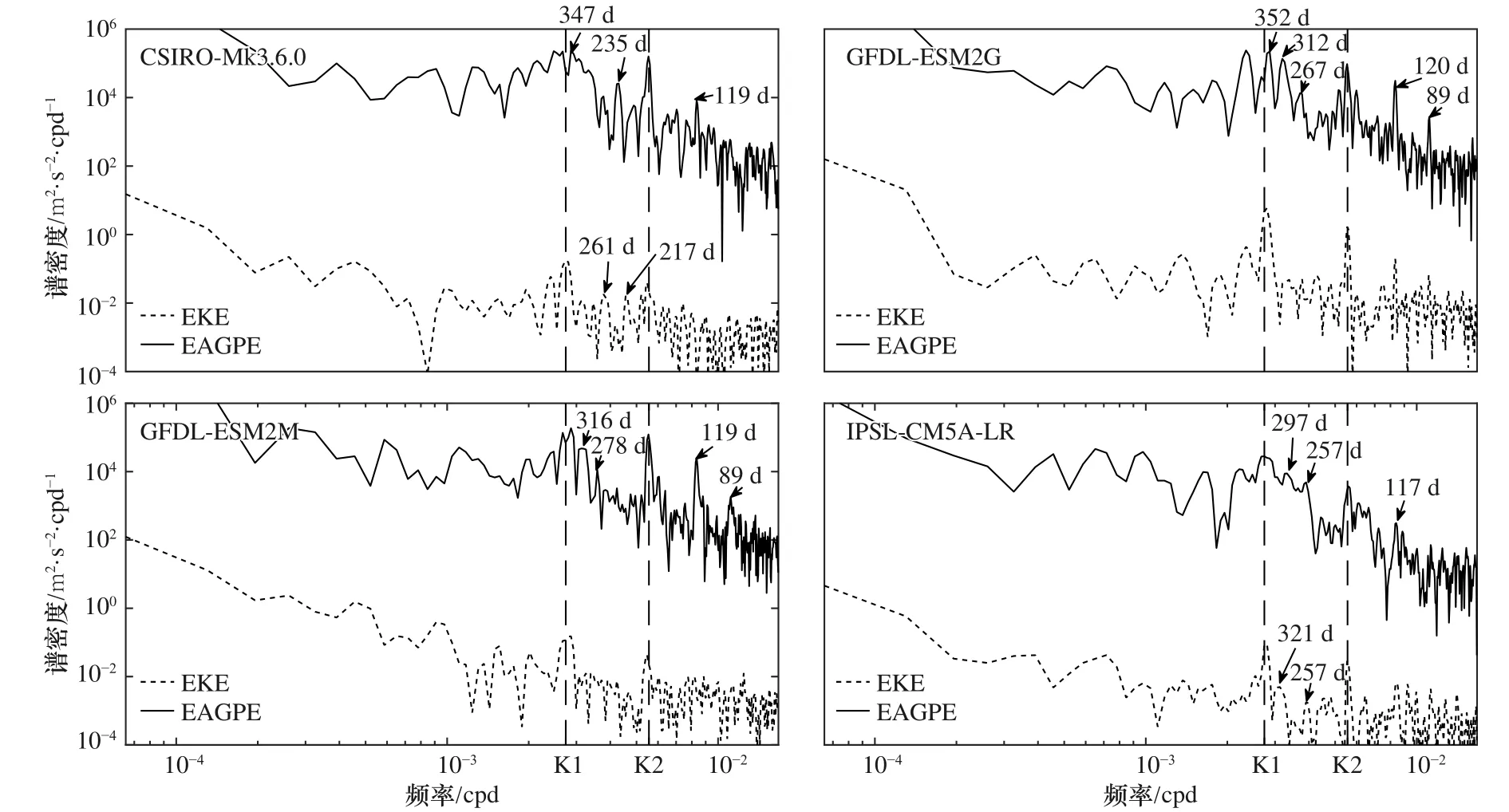
圖13 南大洋區(qū)域渦動能（EKE）與中尺度有效重力勢能（EAGPE）時間序列功率譜Fig. 13 Power spectral of EKE and EAGPE in the Southern Ocean region

表2 渦動能（EKE）與中尺度有效重力勢能（EAGPE）時間序列相關性Table 2 The correlation between the temporal variations of EKE and EAGPE

（4）通過與Argo觀測計算的有效重力勢能進行比較，由 GFDL-CM3、GFDL-ESM2G、GFDLESM2M與HadGEM2-ES 4個模式結果所計算的中尺度有效重力勢能從量值大小和空間分布上均與觀測比較接近，其中又以GFDL-ESM2G模式的結果最優(yōu)。由GISS-E2-R模式結果所計算的中尺度有效重力勢能整體偏低，特別是在赤道地區(qū)；而由CanESM2模式結果所計算的中尺度有效重力勢能顯著高于由Argo觀測計算的值。