一種飛機大尺寸曲面測量點差異性規劃方法

毛喆，李瀧杲，*，徐巖，曾琪，主逵

（1.南京航空航天大學 機電學院，南京210016； 2.深圳市勁拓自動化設備股份有限公司，深圳518101）

現代飛機高機動、高氣動的產品需求對裝配質量優化提出了巨大挑戰，數字化測量作為飛機裝配中的重要環節，測量質量的優劣性嚴重影響飛機的實際裝配結果。目前高精度、高效率的數字化測量技術正逐步代替傳統的檢測方式，但測量實施前需基于模型進行測量規劃：一是測量點規劃，二是測量設備站位規劃。前者是后者乃至測量實施的基礎，后者是前者優化的依據。測量點規劃是將待測特征離散為一組點作為理論測量點（簡稱測量點），用于站位規劃、測量實施、模型重構、質量分析等環節，但當前測量點規劃依賴于工藝人員經驗，缺乏理論依據與評價機制，極易出現測量效率低、實測數據分析量大等問題。因此，合理規劃測量點對測量效率、測量精度的提升具有重要意義。

Cho等［1］根據待測曲面面積、測量精度等因素利用模糊神經網絡確定布點數量，為三坐標測量機布點提供了依據，但在布設過程中未考慮到自由曲面的復雜性。Lee等［2］結合Hammersley序列提出了一種布點方法，有效地減少了布點數量。宋占杰等［3］將自由曲面的曲率函數作為生成質心Voronoi結構中的密度函數，以成本函數收斂性作為算法結束準則，提出了一種全新的基于質心Voronoi的檢測點采樣方法。劉紅軍等［4］提出了實時重構布點策略，但需要在測量時對測量數據實時重構，測量效率低下。此外，諸多學者對測量點布設展開了研究，但多以特征的曲率特性作為測量點布設依據，并未考慮實際的測量不確定度［5-6］。激光雷達等測量設備在測量距離較遠時，測量不確定度會達到甚至超過0.1mm，此時的測量數據難以精準反映零件的實際狀態，需要采用相關算法減小測量不確定度。

本文采用非均勻有理B樣條（Non-Uniform Rational B-Spline，NURBS）理論精確擬合自由曲線或曲面，并利用粒子群優化算法優化控制點和權因子提高擬合精度。對待測特征進行區域劃分，包括曲率極值區和測量不確定度較大區，并針對不同的區域設計相應的布點策略確保測量點能夠精確地表達待測特征。在有效保證測量效率的前提下，使測量點逆向重構特征與理論特征偏差優于10-3mm。

1 問題描述

對于復雜飛機零部件而言，曲面特征多以自由造型設計，測量點規劃主要取決于工藝人員的經驗。過多的測量點會延長測量周期，過少的測量點無法精確測得零件的實際狀態。此外，當前測量點布設大多以曲率特性作為依據，忽視了測量不確定度對測量結果的影響，測量不確定度較大位置測量數據有時難以反映零件的實際狀態。即使可以增加設備站位減小測量不確定度，但隨之產生的是測量效率降低、數據轉換誤差累積等問題。

試驗件曲率極值區域及測量不確定度較大區域分布如圖1所示。圖中曲率極值區域并未完全覆蓋測量不確定度較大區域，在盡量避免轉站前提下，僅以曲率作為布點依據難以精準測得零件的實際狀態。

圖1 試驗件測量不確定度及曲率分布Fig.1 Measurement uncertainty and curvature distribution of test piece

2 待測特征確定性表達構建

飛機大尺寸零部件待測特征主要為曲線、曲面等基本特征，曲面特征一般是通過離散為一組曲線、采用NURBS精確擬合各條曲線進行分析。鑒于3次NURBS曲線具有C2連續性且能夠滿足工程中的造型需求［7］，本文的研究基于3次NURBS曲線展開。

2.1 曲線方程參數化

一條p次NURBS曲線可定義為［8］

式中：Ni，p為Bernstein基函數；u為自由變量。

自由曲線表征為NURBS初始需求解控制點Vi、權因子wi及節點矢量U，其中節點矢量通過弦長參數化確定。權因子和控制點的耦合求解過程復雜，極易出現奇異解或無解的情況，為簡化計算，令wi初始值為1，控制點可由式（2）解得：

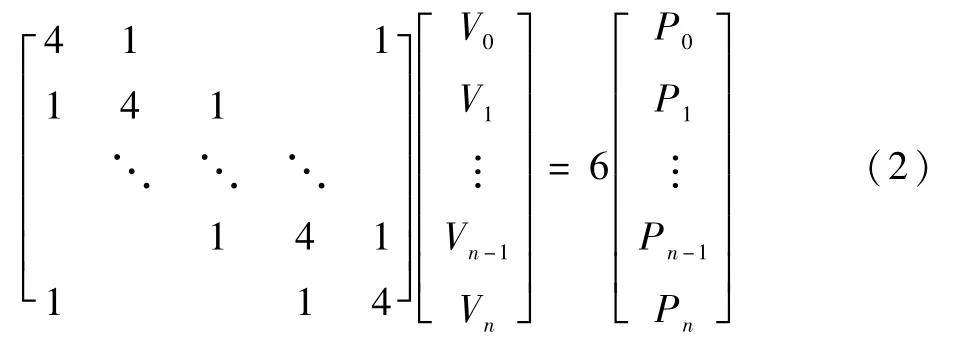
式中：Pi為型值點。

控制點求解后曲線初始方程r0（u）為

式（3）確定的擬合曲線往往不能精確表達理論曲線，一般采用增加型值點的方式提高擬合曲線的精度，但型值點數量增加到一定程度后對曲線精度的提高效果不明顯，有時甚至會產生扭曲和畸變［9］，需要對wi和Vi進行優化提高曲線的擬合精度。

2.2 參數化方程優化

2.2.1 局部優化

NURBS曲線形狀可通過調節控制點和權因子進行修改，權因子wi負責曲線形狀的局部修改。針對擬合曲線中局部區域偏離理論曲線的情況，可通過調節wi提高曲線的擬合精度，如圖2所示。

設調整后權因子為w′i，wi與w′i的關 系可表示為［10］式中：d為擬合曲線與理論線間的最大偏差。

圖2 權因子對曲線形狀的影響Fig.2 Influence of weight factor on curve shape

對于僅有少數幾個部位誤差較大的情況，依據式（4）對曲線形狀微調，重復采用此方法快速提高參數方程正確性。但是對于整體偏離理論曲線的情況，修改的權因子數量多，優化效率低。

2.2.2 整體優化

曲線的整體優化方法為對Vi及wi共同調整，但由于當前控制點和權因子間未形成確定的關系式，調整過程中Vi和wi的設置直接影響優化結果及速度。鑒于粒子群優化算法［11］具有收斂速度快、參數少等優點，本文采用粒子群優化算法對Vi及wi進行優化。

以一組控制點及其權因子作為一個優化粒子Zj，優化問題解的維度D＝4n（n為控制點個數，x，y，z為控制點坐標），第j個粒子定義為

設第j個粒子的最優位置為Pbestj，整個群體經歷的最優位置為Gbest，第j個粒子的速度及位置更新公式分別為

式中：w為慣性權重；c1、c2為學習因子；rand1、rand2為0～1之間的隨機數。設第j個粒子Zj構成的NURBS曲線為rkj（u），將rkj（u）進行離散，計算每個離散點到理論線的最小距離，形成距離集Dj＝｛dj1，dj2，…，djm｝（m為離散點個數），構造適應度函數為

式中：F為粒子個數。結合局部優化和整體優化方法，待測特征精確參數化總體流程如下：

步驟1 采用等弦長法將理論線r離散為一組型值點P＝｛P0，P1，…，Pn｝，以P為初始條件計算初始曲線方程r0（u）并生成擬合曲線。

步驟2 計算擬合曲線與理論線的最大偏差δ，若δ大于給定閾值ε0，回到步驟1增加型值點數量以減小δ，否則執行步驟3。

步驟3 判斷擬合曲線與理論線偏離狀態，若兩曲線偏離距離δ小于閾值ε1，執行步驟7；若局部偏離執行步驟4；若整體偏離執行步驟5。

步驟4 計算r與擬合曲線最大偏差δ，按式（4）修改權因子形成新的曲線方程rk（u）。計算r與rk（u）的最大偏差δ，執行步驟5。

步驟5 若δ大于閾值ε1，重復步驟4修改下一處權因子，直到δ變化不明顯或小于ε1，執行步驟7。

步驟6 采用粒子群優化算法對控制點及權因子整體優化，若δ變化不明顯或小于ε1，執行步驟7。

步驟7 輸出最終的控制點、權因子及參數化曲線方程r（u）。

3 待測特征測量點布設

飛機大型結構件、薄壁等零件易產生裝配變形，曲率較大的位置變形較難控制［12］，且在測距較遠時測量不確定度較大，測量結果不準確。針對上述情況，綜合考慮曲率特性和測量不確定度等因素布設測量點。

3.1 曲線測量點布設

3.1.1 曲率極值點求解

曲率極值點是描述曲線形狀的關鍵點，為了獲取曲率極值處的變形情況，需要在曲率極值點處布設測量點。設曲線的參數方程為r（u）＝｛x（u），y（u），z（u）｝，空間曲線在某一處的曲率k（u）表示為［13］

式中：r′（u）與r″（u）分別為曲線r（u）的一階導數與二階導數，將其代入式（9）可得

對k（u）求一階導數為

曲率極值點為?k／?u＝0的解，但此方程求解過于復雜，針對這種情況本文提出了一種基于曲率導數的曲率極值點快速定位方法，具體方法流程如下：

步驟1 將曲線方程r（u）離散，記錄每個離散點對應的ui。

步驟2 計算每個離散點的曲率導數J（ui），J（ui）＝?k／?u｜u＝ui。

步驟3 計算相鄰兩點曲率導數積Di＝J（ui）·J（ui+1），執行步驟4。

步驟4 遍歷所有的Di值，對Di≤0的兩點T0、Q0和ui、ui+1保存，對保存的點對逐一執行步驟5和步驟6。

步驟5 取ui、ui+1的中間值um代入r（u），在T0、Q0中間生成點M0。分別計算J（um）·J（ui）與J（um）·J（ui+1）的值。若J（um）·J（ui）≤0，以中間點取代Q0，反之，以中間點取代T0。執行步驟6。

步驟6 重復步驟5更新T0、Q0，直到T0、Q0距離小于給定閾值ε2，以兩點中間點作為曲率極值點。

圖3為曲線某一個曲率極值點求解，左邊界由T0更新至T4，右邊界點由Q0更新至Q4。

圖4為某零件邊界曲線的曲率極值求解，圓“·”為采用本文方法求解出的曲率極值點，“”為CATIA（Computer Aided Three-dimensional Interactive Application）中曲率變化曲線上的極值點。從圖中可以看出，采用本文方法求解的曲率極值與CATIA中的曲率極值基本一致。

圖3 曲率極值點搜索Fig.3 Search of curvature extreme points

圖4 曲線曲率極值點求解結果Fig.4 Solving result of curve curvature extreme points

3.1.2 測量不確定度評估

為降低測量不確定度對測量結果的影響，在測量不確定度較大區域加密布設測量點，通過間接平差的方式減小此影響。本文以球坐標測量系統為研究對象對測量不確定度評估。任一測量點M（x，y，z）在測量坐標系的坐標可由距離l、方位角α及天頂角β解得。

由于設備、環境因素，l、α、β采集的過程中均存在著一定的誤差，為評價測量點在空間的不確定度，建立不確定度橢球模型［14-15］如圖5所示。

不確定橢球的半軸長Ux′、Uy′、Uz′分別為［16-17］

式中：σα、σβ與測量系統的角度編碼器分辨率有關，為儀器制造商提供的固定值；σl由最小測距不確定分量和測距不確定度距離放大系數組成。

圖6為曲線輪廓度及測量不確定度允許偏差示意圖，測量不確定度允許偏差范圍一般為輪廓度的十分之一。圖中兩端及曲率較大處測量不確定度橢球較大，有的甚至超出不確定度允許偏差范圍。為了減小測量不確定度，提出一種以測量不確定度為依據的測量點布設方法。具體流程如下：

步驟1 選取合適位置作為測量設備站位E（x，y，z）。

步驟2 根據曲線方程r（u），對曲線進行離散，生成離散點集G＝｛G0，G1，…，Gn｝。

圖5 不確定度橢球模型Fig.5 Uncertainty ellipsoid model

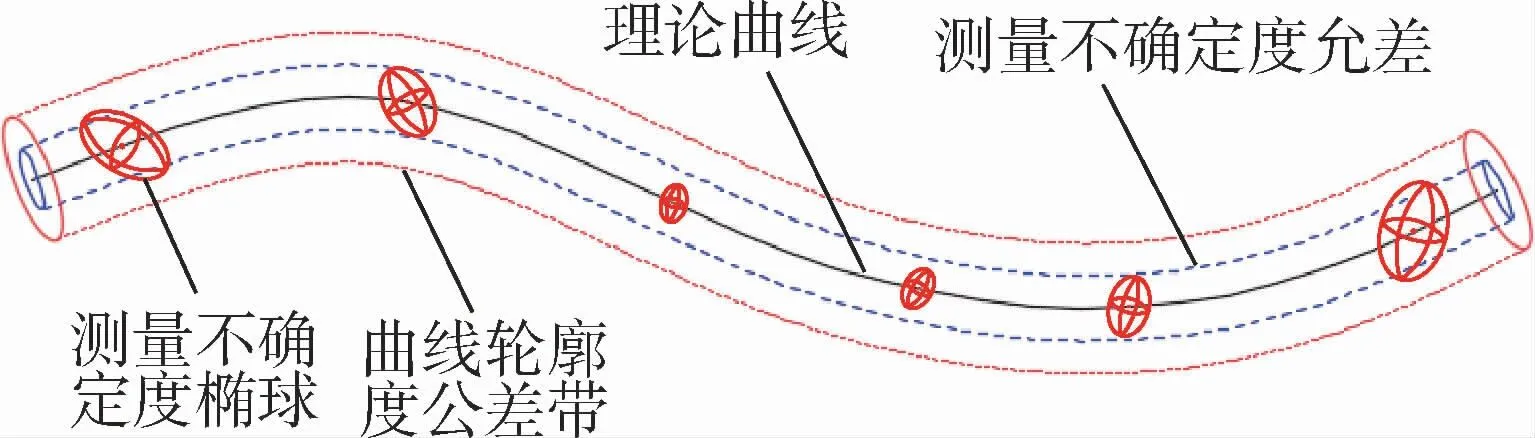
圖6 曲線輪廓度公差帶及測量不確定度允差Fig.6 Tolerance zone and measurement uncertainty tolerance of curve

步驟3 計算每個離散點Gi到E的距離li，根據式（13）計算出每個橢球的半軸長。

步驟4 以Gi為原點，Gi與E連線為u軸，在x′-y′-z′坐標系構建單側不確定度橢球并生成橢球離散點。

步驟5 通過坐標轉換將不確定度橢球離散點由x′-y′-z′坐標系轉換到x-y-z坐標系中。

步驟6 計算每個橢球離散點距離理論線的最遠點，將最遠點擬合成為一條曲線，對其進行光順后作為不確定度曲線。

步驟7 在不確定度曲線超出不確定度允許范圍的區域布設若干測量點。

3.2 曲面測量點布設

曲面測量點布設是將曲面離散成為一組截交線［18］，按照3.1節方法對每條截交線布設測量點。大尺寸曲面測量過程中，測量數據同樣存在測量不確定度，圖7為曲面輪廓度公差帶和測量不確定度允差的分布情況。為了減小測量不確定度的影響，構建每個測量點的單側不確定度橢球并生成橢球離散點，找出離散點中距離理論面最遠點。將最遠點擬合成為不確定度曲面，計算出不確定度曲面超出不確定度允許偏差范圍的區域，并在這些區域加密布設測量點。最后將截交線離散點及根據測量不確定度增加的測量點進行篩選，對于距離過小甚至重合的兩點取中間點代替。

采用上述布點策略布設的測量點有時無法精確描述理論特征，需要對測量點補充。測量點補充方法是將依據曲率及測量不確定度布設的測量點進行重構，找出重構特征與理論特征偏差較大位置，并在該位置補充測量點。以測量點重構曲面與理論曲面的最大距離偏差作為測量點能否精確描述待測特征的指標，待測特征測量點布設整體流程如圖8所示，圖中ε3為重構特征與理論特征的閾值。

圖7 曲面輪廓度公差帶及測量不確定度允差Fig.7 Tolerance zone and measurement uncertainty tolerance of surface

圖8 測量點布設流程Fig.8 Process ofmeasurement points distribution

4 實驗驗證

為實現曲線曲面的自動布點，在CATIA［19］環境下利用CAA［20］（Components Application Architecture）技術開發測量點布設模塊。軟件實現包含特征預處理、特征分析及測量點規劃、測量點輸出3部分，如圖9所示。

以圖1中的試驗件作為驗證對象，首先提取如圖10（a）所示的待測特征；隨后進行特征分析和測量點布設，將曲面離散為一組截交線，對截交線按照3.1節方法規劃測量點，求解出測量不確定度較大區域，并在該區域采用3.2節布點方法加密布設測量點，測量點布設結果如圖10（b）所示；最后輸出測量點，如圖10（c）所示。為使參數方程和測量點精確擬合待測特征，閾值ε1、ε1優于10-3mm。為達到測量不確定度較大區域加密布點的目的，此區域測量點重構閾值取普通區域閾值ε3的一半。

圖9 自動布點模塊架構Fig.9 Architecture of automatic points distribution module

圖10 試驗件局部曲面片布點過程Fig.10 Points distribution process of partial surface of test piece

表1為粒子群優化算法所采用的參數，vmax、vmin分別為最大、最小更新速度，Np為迭代次數。

為驗證布點合理性，采用傳統布點方法在試驗件上布點密度為20×20和10×10的測量點，如圖11（a）和圖11（b）所示，圖11（c）為采用本文方法布設的測量點。利用激光雷達MV260作為測量工具（其角度精度6.8μm／m，距離精度10μm+2.5μm／m），對3種情況進行現場測量。

分別構建3種布點方法中的理論點的單側不確定度橢球，將不確定度橢球離散，計算每個橢球離散點集中距離理論面的最遠點，將最遠點擬合為不確定度曲面，以不確定度曲面距離理論面的最大距離作為擬合精度，3種布點方法的測量效率及擬合精度如表2所示。試驗件測量點分布情況如圖12所示。

表1 粒子群優化算法參數Tab le 1 Param eters of par ticle swarm optim ization algorithm

圖11 不同布點密度布點結果對比Fig.11 Comparison of points distribution under differentmeasurement points density

表2 不同布點密度下測量結果對比Table 2 Com parison of m easurem ent result under different m easurem ent points density

圖12 試驗件測量點分布Fig.12 Measurement points distribution of test piece

從表2中可以看出，采用本文方法布點測量效率介于布點密度為10×10和20×20之間，重構的孔洞數量、擬合精度與布點密度為10×10的結果相當，但明顯優于布點密度為20×20的測量點重構的孔洞數量及擬合精度，充分體現了本文布點策略的合理性及可行性。

5 結 論

針對航空大尺寸零部件測量點規劃的基礎問題，本文分別從待測特征曲率特性、測量不確定度角度出發對測量點進行規劃，研究了測量點布設的理論依據及布設方法。主要結論如下：

1）將待測特征精確參數化，并對參數方程優化實現擬合精度優于10-3mm，為復雜特征的曲率及測量不確定度分析提供依據。

2）為復雜曲線曲面測量點規劃提供了理論依據，在保證測量點精確表征待測特征的條件下控制測量點數量，使測量點逆向特征與理論特征的最大偏差優于10-3mm。

3）開發了測量點自動布設模塊，提高測量點布設效率及規范性。