平面正弦鋼球傳動機構接觸力影響因素分析

寧林飛, 李美求, 羅競波

(長江大學機械結構強度與振動研究所，荊州 434023)

隨著航空航天、機器人工業(yè)、石油鉆井以及交通運輸?shù)裙I(yè)領域的高速發(fā)展，工業(yè)領域對活齒傳動機構的結構尺寸、承載能力、傳動效率、傳動比范圍提出了更高的要求[1-2]。目前，中外學者針對活齒傳動機構的傳動性能[3-6]、強度計算[7-9]、模態(tài)分析[10-12]、力學特性[13-15]及動力學仿真[16-17]等方面進行了深入的研究。

其中，韓國學者Nam等[5]為機器人設計了一種球齒薄板減速器，通過分布在凹槽中的兩排滾珠來降低減速器工作過程中的壓應力，從而提高機器人的工作性能。李沖等[11]設計了一種大傳動比微型活齒傳動機構，兼顧考慮了嚙合齒數(shù)變化引起的非線性效應，建立了活齒傳動系統(tǒng)的非線性動力學方程。曹富林等[14]根據(jù)半無窮空間理論，應用范德華勢函數(shù)，推導出活齒受范德華力的公式，建立了微型集成活齒傳動系統(tǒng)中任一活齒不同嚙合位置處的靜力學方程。袁新梅等[15]研究了圓柱正弦活齒傳動中主要結構參數(shù)對嚙合副接觸力的影響，總結出嚙合副接觸力大小和周期的變化規(guī)律。

上述研究成果不僅豐富了活齒減速器的類型，而且進一步完善了活齒傳動機構的設計理論體系，拓寬了活齒傳動機構在工業(yè)領域的應用范圍。然而，關于平面正弦鋼球傳動機構接觸力影響因素的研究卻很少，使其在石油鉆井行業(yè)中的應用缺少科學的理論依據(jù)。因此，以鋼球接觸力的影響因素為研究對象，建立力學模型，采用控制變量的方法，研究平面正弦鋼球傳動機構的基本結構參數(shù)對接觸力特性的影響，并以此為基礎歸納出平面正弦鋼球傳動機構設計中應當遵循的規(guī)律。

1 平面正弦鋼球傳動機構受力分析

平面正弦鋼球傳動機構的主要零部件有殼體、主動圓盤、保持架、從動圓盤以及鋼球等，如圖1所示。主動圓盤與從動圓盤在沿圓周方向上分布著平面正弦曲線槽。鋼球活動槽均勻地分布在保持架上，并且處于主動圓盤與從動圓盤兩個平面正弦曲線槽的交匯處。由于活動槽在保持架上均勻排布，每個活動槽中鋼球的運動學特性和力學特性完全相同，因此分析該傳動機構的受力情況時可取任一活動槽中的鋼球為研究對象。

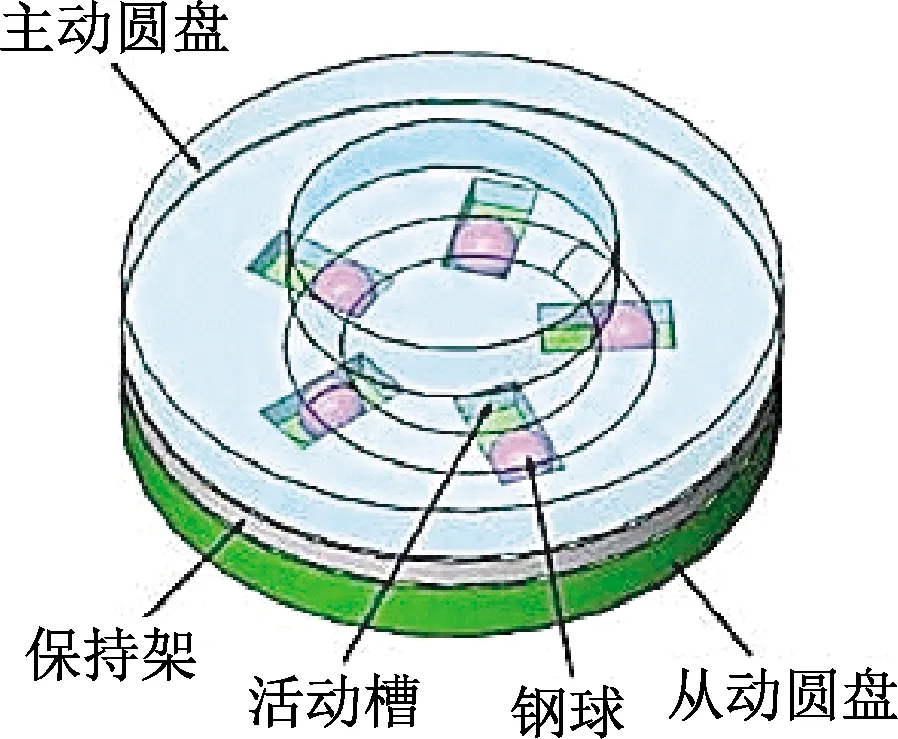
圖1 平面正弦鋼球減速器結構示意圖

1.1 鋼球受力分析平衡方程

鋼球局部坐標系為(O，i，j，k)，其中坐標原點O為鋼球的球心，i、j、k軸分別代表鋼球運動的軸向、周向及徑向。鋼球運動過程中處于動平衡狀態(tài)，受力如圖2所示，根據(jù)各個力的空間平衡關系有[13]：

F3cosα2-F1cosα1=0

(1)

F3sinα2cosμ2-F1sinα1cosμ1-F2=0

(2)

F3sinα2sinμ2-F1sinα1sinμ1-Fc=0

(3)

式中：F1為主動圓盤的正弦軌道對鋼球的接觸力；F2為保持架的活動槽對鋼球的接觸力；F3為從動圓盤的正弦軌道對鋼球的接觸力；α1、α2分別為F1、F3與坐標軸i的夾角；μ1、μ2分別為F1、F3在鋼球坐標系jOk平面上的投影與周向的夾角；Fc為鋼球的慣性力。

圖2 鋼球受力分析圖

主動圓盤、從動圓盤與鋼球的嚙合方程為

(4)

(5)

式中：A為正弦曲線振幅；R為法線圓半徑；主動圓盤上的平面正弦曲線槽周期N1；從動圓盤上的平面正弦曲線槽周期N2；φ1為主動圓盤相對于固定保持架的轉動角度；φ2為從動圓盤相對于固定保持架的轉動角度。

1.2 變形協(xié)調方程和幾何方程

假設鋼球與主動圓盤、從動圓盤、保持架這三者之間均為彈性小變形范圍的接觸，可建立出如下變形協(xié)調方程：

(6)

式(6)中：T為從動圓盤的負載力矩。

同時，鋼球在運動過程中滿足如下幾何關系：

(ro-r)cosα1+(ro-r)cosα2+2r=H

(7)

式(7)中：ro為主動圓盤及從動圓盤的正弦軌道截面圓半徑；r為鋼球半徑；H為主動圓盤正弦軌道最低點到從動圓盤正弦軌道最低點之間的垂直距離。

2 結構參數(shù)對接觸力影響分析

在平面正弦鋼球傳動機構設計中，為了確保設計出科學合理和優(yōu)化可靠的傳動機構，有必要研究平面正弦鋼球傳動機構中鋼球接觸力的變化規(guī)律。將實際應用經(jīng)驗與力學理論相結合，可得出如下研究準則。

為了便于加工制造，取主動圓盤上的平面正弦曲線槽周期N1=1，因此只需要考慮從動圓盤上的平面正弦曲線槽周期N2對傳動機構接觸力的影響；正弦曲線振幅A、平面正弦曲線槽周期N2、法線圓半徑R以及正弦軌道截面圓半徑ro不僅決定了平面正弦鋼球減速器結構的緊湊性和加工工藝的復雜程度，而且還對主動圓盤的正弦軌道對鋼球的接觸力F1、保持架的活動槽對鋼球的接觸力F2及從動圓盤的正弦軌道對鋼球的接觸力F3的數(shù)值大小和變化特性有著顯著地影響；慣性力Fc數(shù)值很小，幾乎不影響實際工程問題，可忽略A、N2、R及ro對慣性力Fc的影響。因此，可初步確定以A、N2、R及ro為主要研究對象，分析其對接觸力Fi(i=1，2，3)的影響因素。

采用控制變量的方法，研究參數(shù)A、N2、R及ro單獨變化時對接觸力Fi(i=1，2，3)的影響規(guī)律，接觸力的數(shù)值求解可在MATLAB中使用Newton-Ra-phson迭代的方法得以實現(xiàn)。A、N2、R及ro在3個水平上的取值與原始數(shù)據(jù)取值如表1所示。

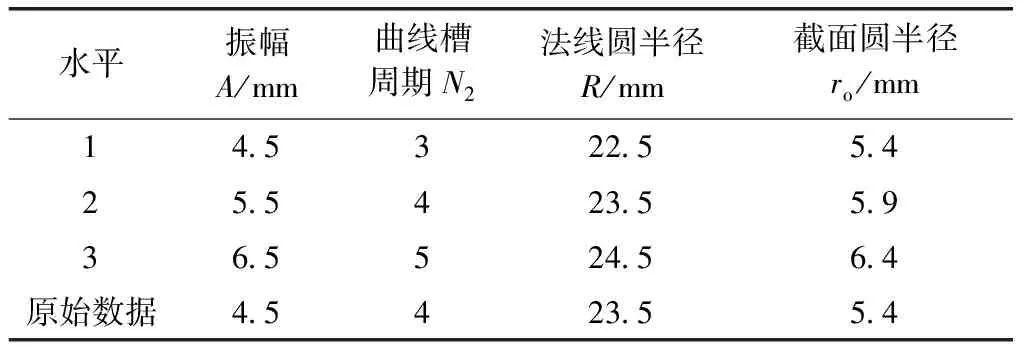
表1 結構參數(shù)與取值

2.1 正弦曲線振幅A對接觸力的影響

正弦曲線振幅A不僅影響接觸力的曲線特性而且還決定該機構的徑向幾何尺寸。根據(jù)設計經(jīng)驗A一般不能低于3.5 mm，而A超過6.5 mm時，會極大地影響接觸力F1的特性，不利于鋼球在活動槽中的平穩(wěn)運動。因此，A分別取為4.5、5.5、6.5 mm，繪制出如圖3所示的接觸力隨主動圓盤轉角φ1的變化曲線。

由圖3可知，隨著正弦曲線振幅A的增大，接觸力Fi(i=1，2，3)隨之增大；當A=6.5 mm時，接觸力F1的曲線特性發(fā)生改變，在波峰處出現(xiàn)畸形；接觸力Fi(i=1，2，3)的最小值Fi，min均為0且不隨A的值發(fā)生變化。

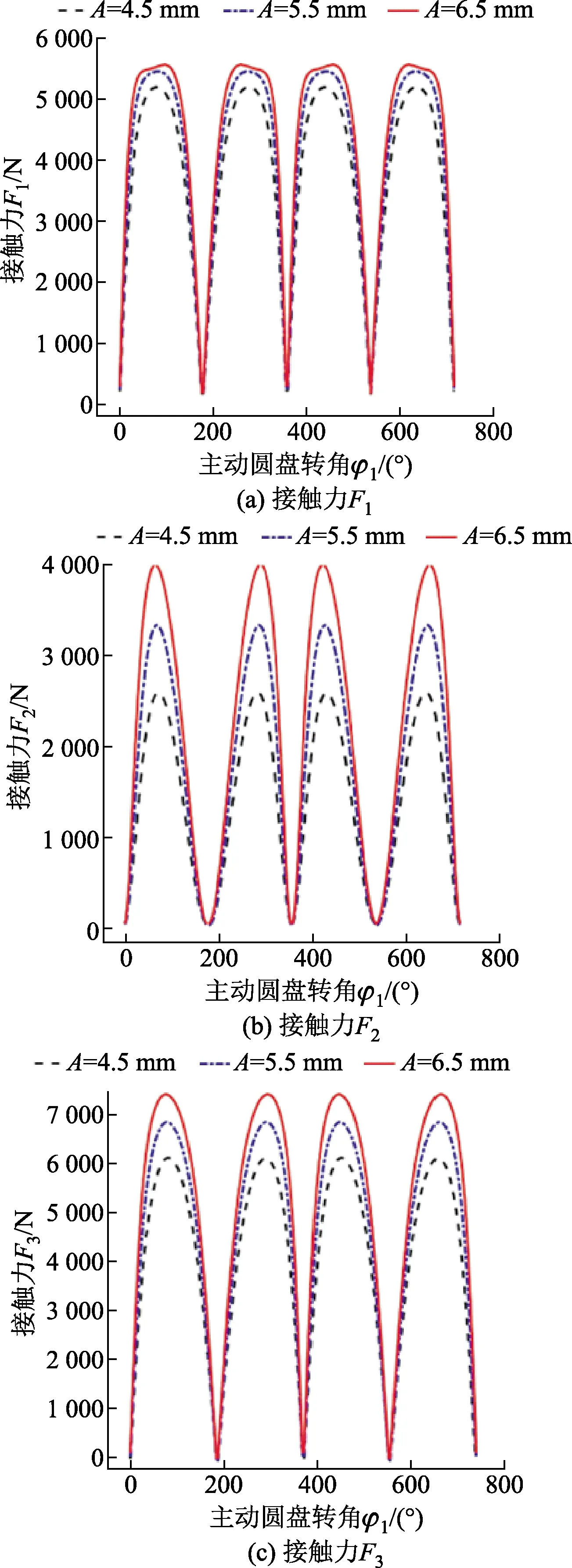
N2=4，R=23.5 mm，ro=5.4 mm

2.2 平面正弦曲線槽周期N2對接觸力的影響

平面正弦曲線槽周期N1、N2是該機構中的重要結構參數(shù)，決定了機構的傳動比和鋼球活動槽的數(shù)量。當N2取值過小時，傳動機構的傳動比較小；當N2取值過大時，會加大主動圓盤與從動圓盤加工時的切削量，從而降低傳動機構的結構強度。根據(jù)平面正弦鋼球傳動機構的應用經(jīng)驗，N2可取3、4、5，繪制出如圖4所示的接觸力隨主動圓盤轉角φ1的變化曲線。

由圖4可知，隨著平面正弦曲線槽周期N2的增大，接觸力Fi(i=1，2，3)也隨之增大且周期不發(fā)生改變；當N2分別為3、4、5時，與之相對應的傳動比n為3、4、5，這就意味著增大傳動機構的傳動比會導致接觸力的增大。

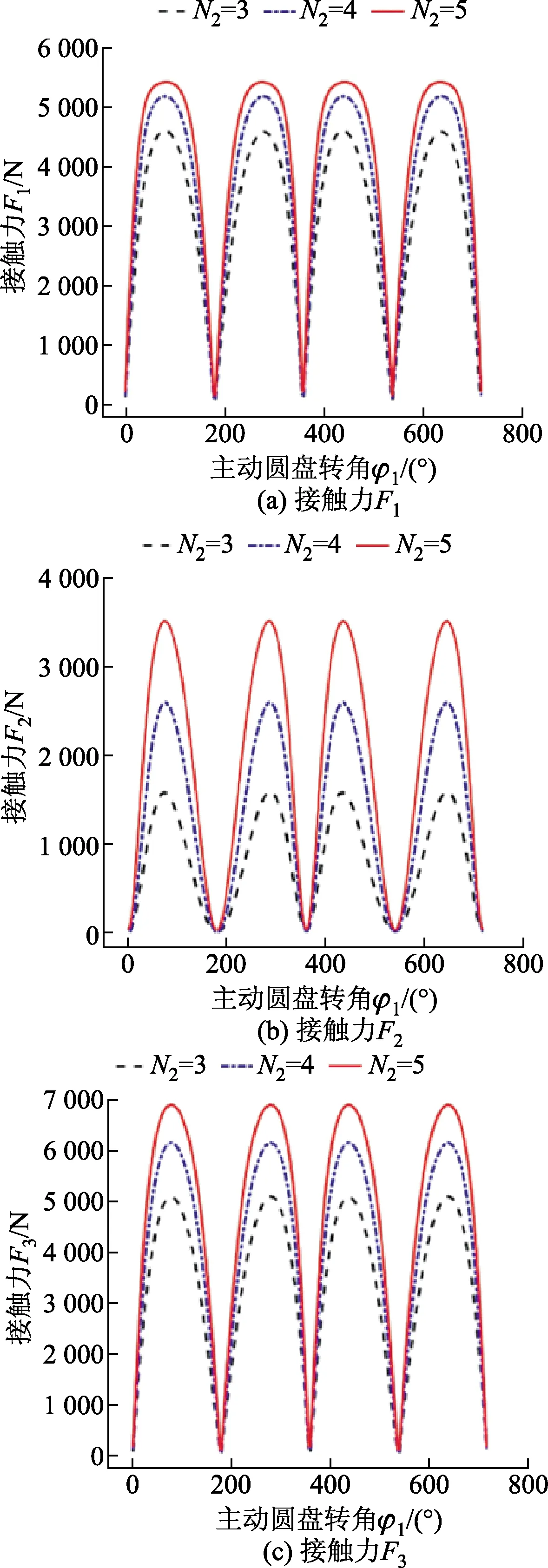
A=4.5 mm，R=23.5 mm，ro=5.4 mm

2.3 法線圓半徑R對接觸力的影響

法線圓半徑R決定了活動槽在徑向方向的分布位置，從而影響了該機構徑向幾何尺寸的大小。由于平面正弦鋼球傳動機構用于小井眼鉆井作業(yè)中，其結構的公稱外徑不能過大，并且一定要小于井壁內徑；同時，適當?shù)丶哟蠓ň€圓半徑R有利于降低接觸力Fi(i=1，2，3)的值。所以，根據(jù)設計經(jīng)驗R分別取為22.5、23.5、24.5 mm，繪制出如圖5所示的接觸力隨主動圓盤轉角φ1的變化曲線。

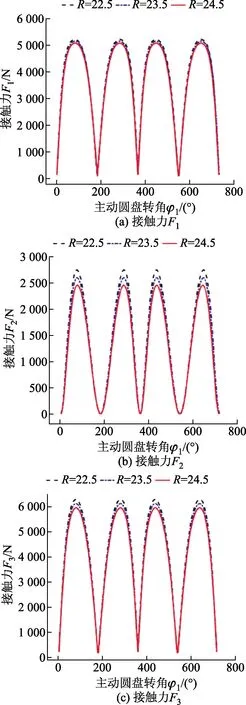
A=4.5 mm，N2=4，ro=5.4 mm

由圖5可知，隨著法線圓半徑R的增大，接觸力Fi(i=1，2，3)隨之減小，但減少幅度很小；接觸力曲線特性幾乎不發(fā)生變化，只是在波峰附近有略微的差異。

2.4 正弦軌道截面圓半徑ro對接觸力的影響

正弦軌道截面圓半徑ro決定了鋼球沿周向方向的運動狀態(tài)和接觸力與坐標軸的夾角，從而在一定程度上影響了接觸力的曲線特性。由于鋼球半徑為5 mm，正弦軌道截面圓半徑ro必須大于鋼球半徑，又考慮到ro的微小變化對機構與接觸力在周向以及徑向方向上的夾角影響甚大。所以，ro分別取為5.4、5.9、6.4 mm。當ro分別為5.4、5.9、6.4 mm 時，繪制出如圖6所示的接觸力隨主動圓盤轉角φ1的變化曲線。

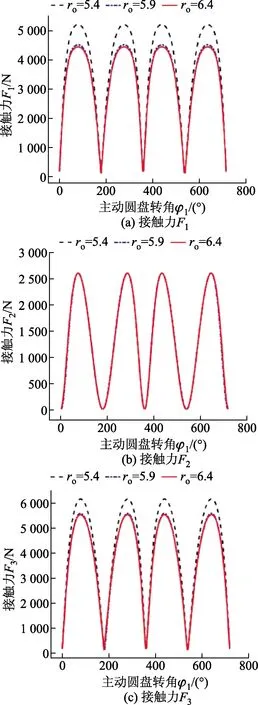
A=4.5 mm，N2=4，R=23.5 mm

由圖6可知，正弦軌道截面圓半徑ro由 5.4 mm 增大到5.9 mm時，F(xiàn)1和F3的值均有所減少，當ro由5.9 mm增大到6.4 mm時，F(xiàn)1和F3幾乎不發(fā)生改變；F2的值與正弦軌道截面圓半徑ro的變化無關。

為了便于直觀研究接觸力數(shù)值大小的變化情況，現(xiàn)統(tǒng)計出接觸力Fi,max(i=1，2，3)在不同參數(shù)水平下的值，其結果如表2所示。比較上述4項結構參數(shù)對接觸力Fi(i=1，2，3)的影響，可以發(fā)現(xiàn)鋼球接觸力存在以下規(guī)律。

曲線槽周期N2對接觸力的影響最為顯著，正弦曲線振幅A、正弦軌道截面圓半徑ro及法線圓半徑R次之，且均不影響接觸力周期的變化。接觸力隨著正弦曲線振幅A和曲線槽周期N2的增大而增大，隨著法線圓半徑R的增大而減小；F1和F3隨著正弦軌道截面圓半徑ro的增大而減小，F(xiàn)2不隨之變化。

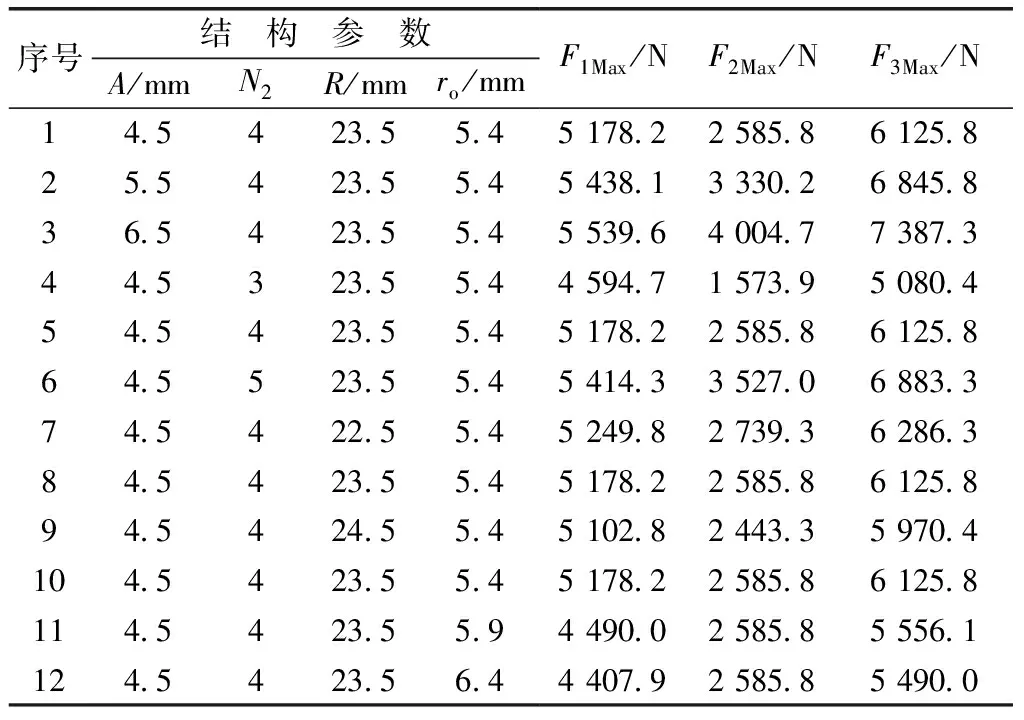
表2 不同參數(shù)水平下的接觸力Fi，max

適當降低A可以減小活動槽鋼球接觸力的大小，但是為了確保機構的傳動特性和結構強度一般取A≥4.5 mm。在確定傳動比n的前提下，取N1=1，N2越小接觸力越小，并且活動槽的數(shù)量也越少，從而提高了保持架的剛度。法線圓半徑R的值對接觸力大小影響最小，增大R雖然可以降低接觸力的值；當R由22.5 mm增大到23.5 mm以及由 23.5 mm 增大到24.5 mm時，其接觸力Fi，max(i=1，2，3)的變化量均為超過6%。增大正弦軌道截面圓半徑ro會加大鋼球與活動槽之間的間隙，不利于鋼球在曲線槽中平穩(wěn)運動，由于F2是活動槽對鋼球沿周向方向上的力，所以F2不受ro的影響；ro由5.4 mm 增大到5.9 mm時接觸力F1,max和F3,max分別降低了13.3%和9.3%，但是當ro由5.9 mm增大到 6.4 mm 時接觸力F1,max和F3,max的變化量均未超過2%。

為了有效地降低接觸力的值，確保機構的穩(wěn)定傳動。將上述分析結果與原始數(shù)據(jù)做比對，可得出如下所示的結構優(yōu)化參數(shù)：A=4.5 mm，N2=3、4、5，R=22.5 mm,ro=5.9 mm。

3 結論

(1)總結出鋼球接觸力曲線特性和數(shù)值大小隨4項基本結構參數(shù)單獨改變時的變化規(guī)律。

(2)在原始數(shù)據(jù)的基礎上得出一組結構優(yōu)化參數(shù)，有效地降低了鋼球接觸力的值，從而提高了該機構的傳動性能。

(3)綜合分析鋼球接觸力曲線特性的變化規(guī)律，歸納出平面正弦鋼球傳動機構在結構設計方面應當遵循的一般設計準則。