基于交叉驗證支持向量機儲層預測方法及應用

張軍華, 任雄風, 趙 杰, 譚明友, 于正軍

(1.中國石油大學(華東)地球科學與技術學院，青島 266580；2.勝利油田物探研究院，東營 257022)

東營凹陷中淺部儲層油氣勘探，大多都形成了技術系列與規范。而深部儲層其成因及成藏機制的研究還不夠深入，地震資料品質相對較差，鉆遇井又比較少，儲層厚度預測有較大的困難。

儲層預測有很多方法，支持向量機方法(SVM)由于能很好地解決樣本少、非線性、高維數和局部極小點問題[1]，對于少井區的儲層預測，是值得優先使用的方法[2-3]。SVM最早由Vapnik根據模式識別中廣義肖像算法發展而來[4-5]，隨著對ε不敏感損失函數的引入[6]，學習性能得到提高，在建模、預測等方面取得了很好的應用效果[7-9]。鄒華勝等將SVM引入少訓練樣本的儲層厚度預測中，預測相對誤差較BP人工神經更小[10]。張長開等通過SVM的屬性優選方法選出有效屬性，基于SVM對儲層進行了有效預測[11]。林年添等利用聚類分析法對用卷積升維形成的各類縱、橫波地震屬性進行降維，將用聚合法得到的多波地震聚合屬性作為SVM的學習集進行含油氣儲層預測，預測儲層邊界更加清晰與實際情況較吻合[12]。SVM儲層預測，關鍵因素有兩個：一是選好核函數，本文采用的是適用于高維、小樣本的高斯徑向基函數；二是調好核函數參數g和懲罰因子C，它們會直接影響SVM泛化能力和預測精度[13-14]。為了使每口井都能參加訓練并且得到驗證，在選取懲罰因子和核函數參數的訓練過程中應用了交叉驗證方法[15]，進一步提高了儲層厚度的預測精度。

1 東營深部儲層井震關系分析及屬性優選

1.1 東營深部儲層特征及機理分析

東營凹陷深層發育紫紅色泥巖或棕紅色砂巖，地質界稱其為“紅層”。由于年代老、埋深大，砂、泥巖波阻抗差異較小，地震反射相對較弱，砂體疊置，致使其研究具有很強的挑戰性，研究成果對拓展油氣勘探領域有重要科研及生產價值。

如圖1所示為研究區王古9井(鉆遇紅層)的過井剖面，可以大致將地層范圍分為紅層上覆地層、紅層和紅層下伏地層，可以看到，紅層以上地層和紅層以下中生界地層成層性都很好，但是中部紅層成層性反而低。結合該井目標層段——孔一段錄井資料(圖2)，可見其速度結構復雜，測井曲線抖動非常多，綜合地震相特征分析，說明紅層是以速度變化很大的薄互層為典型特征。

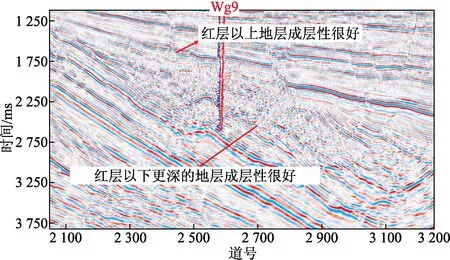
圖1 研究區王古9井過井剖面

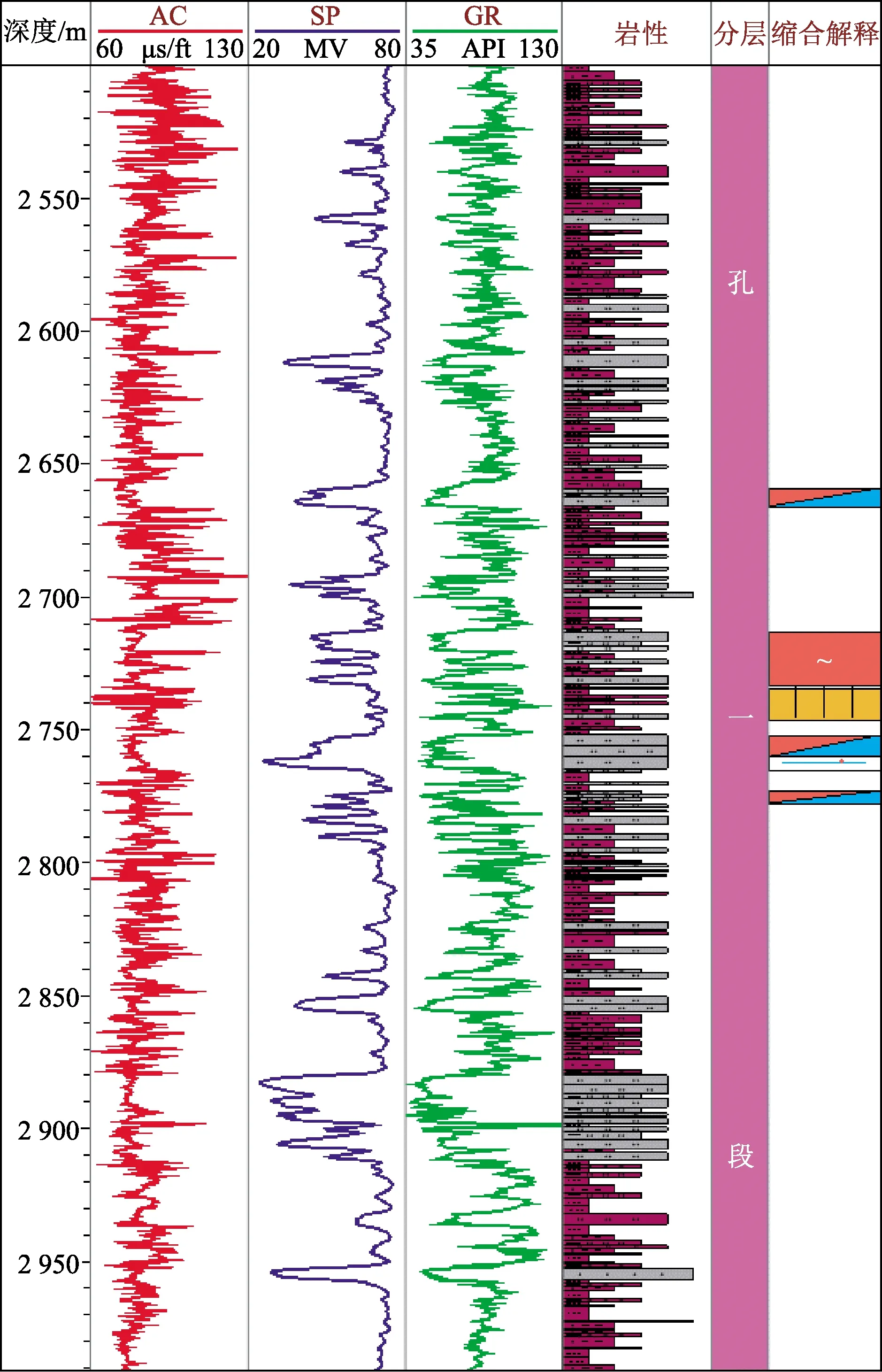
圖2 王古9井孔一段錄井圖

研究區埋深較大，多在3 000 m以上；而面積較大(586 km2)，鉆遇目標層的井卻很少，有可靠測井數據的只有三十幾口。儲層埋深大、層薄、成層性差，地震資料分辨率不夠高，加上鉆遇井少等多種因素，決定著儲層預測有很大的難度。

1.2 地震屬性的提取及優選

地震屬性是地震數據經過數學變換而得來的有關地震波幾何學、運動學、動力學或統計特征，地質含義明確的地震屬性常與儲層有一定的對應關系。對于孔一中儲層，提取振幅、頻率、相位等12種沿層屬性，利用基于核相似性度量的特征選擇方法，優選出帶寬、能量半時、最大振幅、均方根振幅、過零點個數和弧長等6種地震屬性，用于樣本訓練。它們的物理意義和地質含義是明確的：帶寬是指優勢頻帶的寬度，與地震資料的品質相關性較大；能量半時屬性反映了分析時窗內能量相對變化關系，能夠指示沉積環境與巖性巖相變化；最大振幅適合于巖性分析及砂巖百分比研究，儲層含油氣后一般振幅會增強；均方根振幅間接地反映了地震反射系數的大小，可以用來指示地下巖性的變化；過零點個數屬性能夠較好地描述地震波振幅過零點的個數，包含了巖性、流體等信息；弧長屬性是指時窗內地震道波形的長度，對于阻抗差較大的儲層反映效果不錯。

如圖3所示為6種地震屬性和孔一中井點厚度圖。籠統地看，帶寬、能量半時、最大振幅、均方根振幅、過零點個數和弧長6種地震屬性，對孔一中的儲層局部均有較好的相關度，但單個屬性還不能全面描述整個工區儲層變化。為此，要建立井點厚度與屬性的定量關系，用SVM來進行訓練和預測。

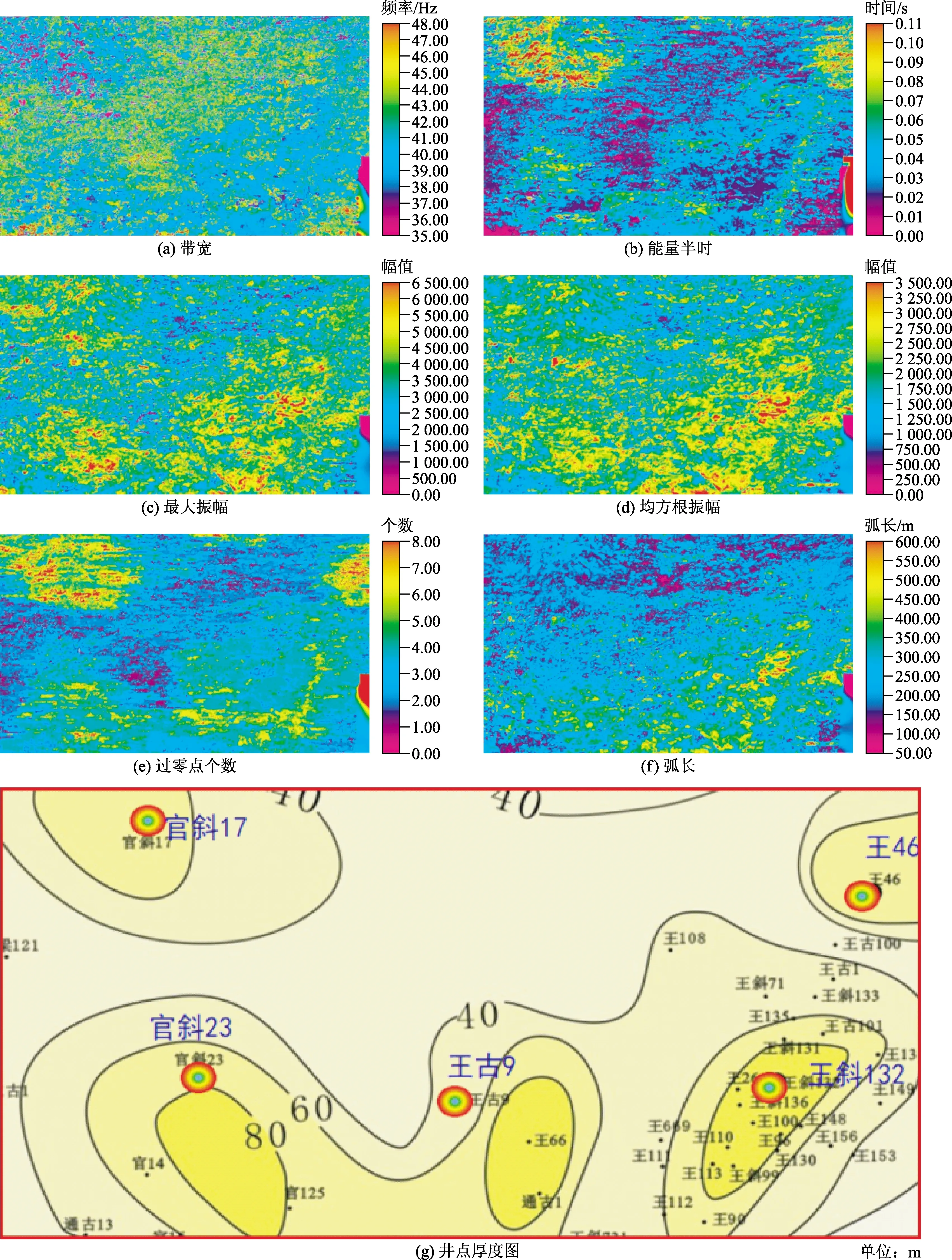
圖3 孔一中地震屬性及井點厚度

2 基于交叉驗證的SVM儲層預測方法

2.1 方法原理

給定樣本集{(xi,yi),i=1,2,…,m},其中xi是輸入數據，yi是與之對應的標簽值，m為樣本個數。SVM回歸具有稀疏性，若樣本點與回歸模型足夠接近，即落入回歸模型的間隔邊界內，則不計算損失，對應的損失函數被稱為ε-不敏感損失函數：

error[y,f(x)]=max[0,|f(x)-y|-ε]

(1)

式(1)中:ε是決定邊界寬度的超參數，訓練學習就是為了使構造的函數f(x)與輸入數據對應目標值y的距離小于ε。當樣本集為非線性時，SVM首先在低維空間中完成計算，而后經過核函數φ(x)將輸入數據x映射到一個高維線性空間，在高維線性空間中完成回歸模型的構建，即：

f(x)=ω·φ(x)+b

(2)

式(2)中：ω是權重向量；b是偏置項。

SVM回歸為式(3)所示的二次凸優化問題：

(3)

由于ε-不敏感損失函數采用max并非處處可導,微分時會有問題,因此使用松弛變量ξ、ξ*進行表示，可得:

(4)

式(4)中：C為懲罰因子；ε為誤差上限。通過引入拉格朗日因子α、α*、μ、μ*，可得式(4)的拉格朗日函數[式(5)]和式(6)所示的對偶優化模型：

L(ω,b,ξ,ξ*,α,α*,μ,μ*)=

(5)

(6)

式中：φ(xi)φ(xj)為核函數，可記為k(xi,xj)。上述對偶問題有如式(7)的KKT條件(一組解是最優解的必要條件)：

(7)

對該對偶問題進行求解，可以得到如式(8)所示的SVM回歸函數形式：

(8)

由式(8)可知，將非線性樣本從低維映射到高維空間只需要計算核函數k(xi,xj)，核函數有多種，選擇高斯徑向基函數，如式(9)：

g>0

(9)

由上述可知，SVM的訓練過程中有兩個重要參數：懲罰因子C和核函數參數g。懲罰因子C用來控制目標函數兩項間的權重，其值大小將影響回歸模型的泛化能力。核函數參數g取值偏小，高次特征衰減速度會很快，可降低空間維數；若取值偏大，則會出現過擬合。在對儲層厚度進行預測時，C和g這兩個參數的取值大小對預測精度至關重要，因此采用了交叉驗證方法對二者進行選取，優選出最優參數。交叉驗證用于評估模型的預測性能，尤其是訓練好的模型在新數據上的表現，可以在一定程度上減小過擬合，還可以從有限的數據中獲取盡可能多的信息。采用k折交叉驗證法，通過對k個不同子集的訓練結果進行平均來減少方差，使模型的性能對數據的劃分不那么敏感。首先將訓練集隨機等分為k份，每次選取一份作為測試集，其他k-1份作為訓練集進行模型訓練，每次訓練得到一個模型，在相應的測試集上測試，k組測試結果的平均值作為當前超參數(懲罰因子C和核函數參數g)下模型精度的估計。在超參數優選范圍內進行訓練，優選出精度最高的預測模型對應的超參數，再對全部訓練集重新訓練得到最優模型。基于交叉驗證SVM儲層預測具體步驟如下。

(1)設置懲罰因子C和核函數參數g的優選范圍Cmin、Cmax、gmin、gmax，以及二者的優選步長ΔC、Δg。

(2)將訓練集隨機等分為n份，令C=Cmin,g=gmin,k=1,i=1。

(3)取第i組作為驗證集，其他組作為訓練數據。

(4)計算訓練后在驗證集上損失函數的大小εi。

(5)令i=i+1,若i≤n，轉到(3)，否則轉到(6)。

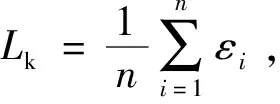
(7)令C=C+ΔC,k=k+1，若C≤Cmax，轉到(2)，否則轉向(8)。

(8)在計算出的損失誤差Lk中選取最小值，其對應的超參數作為最優參數在整個訓練集上重新進行訓練。

2.2 實際資料應用

利用鉆遇孔一中目標層的33口井，從中選取3口井驗證儲層預測效果。將優選出來的帶寬、能量半時、最大振幅、均方根振幅、過零點個數和弧長等6種地震屬性作為輸入數據，以其他30口井點處的屬性值及對應的儲層厚度作為訓練樣本進行訓練。懲罰因子C和核函數參數g的取值按照上述的交叉驗證步驟在一定范圍來優選，令n=6，經訓練得到最優參數C=14、g=3。圖4(a)為用C=14、g=3預測出來的應用工區的儲層厚度，在表1中給出了預留下3口井的預測值以及與實際值的相對誤差，誤差都在10%以下。

如果不采用交叉驗證優選出的參數C和g，預測精度會受到較大影響，圖4(b)是使用非優選出來的參數C=14、g=1預測得到實際工區的儲層厚度圖，在表1中也給出了3口驗證井出的預測值及其與實際值的相對誤差大小，可以看到每口井的預測誤差都有較大增幅，其中W113和Tg1井的誤差都大于14%。結果表明，用交叉驗證優選出的懲罰因子C和核函數g進行儲層預測，可以有效提高預測精度。

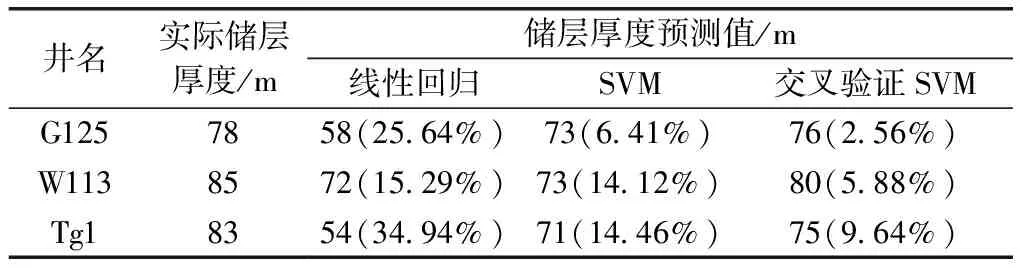
表1 驗證井儲層預測厚度及誤差統計

注：( )中為相對誤差。

用線性擬合方法計算儲層厚度，結果如圖4(c)所示。從驗證井的誤差分析來看，交叉驗證SVM方法要好于不采用交叉驗證的SVM方法，但綜合來看兩種方法都要好于直接擬合的線性回歸方法。

3 結論

東營凹陷孔一段儲層埋深大、層薄、成層性差，地震資料分辨率不夠高，加上鉆遇井少，單一地震屬性僅對儲層局部有較好的相關度，不能全面描述整個工區儲層變化。而SVM算法作為一種基于統計學理論的機器學習算法，在樣本數少的情況下也擁有良好的學習能力和預測精度，要好于直接擬合的線性回歸方法。但要充分發揮SVM的學習和預測性能，懲罰因子C和核函數參數g的選取至關重要，它們對預測精度影響較大。實際資料應用誤差分析表明，交叉驗證SVM方法有較好的預測精度，對中外深部儲層預測有借鑒作用。