基于遺傳算法的渦扇發動機穩態調節規律優化設計

韓文俊，唐 蘭，王 晨，郭海紅

（中國航發沈陽發動機研究所，沈陽110015）

0 引言

航空發動機尤其是軍用發動機裝配飛機后，在飛機起飛、爬升和水平加速時一般工作在中間狀態或最大狀態（全加力狀態），在此過程中發動機發揮其最大推力。為了保證在任何飛行條件下最大限度地發揮發動機潛力[1]，發動機中間或最大狀態的調節規律設計尤為重要。在該設計過程中應綜合考慮發動機的強度負荷、熱負荷和工作穩定性，還需考慮飛機進氣道的流量限制等因素，該設計過程是1個需要人工反復迭代的過程，因此研究出合適的優化設計方法提高設計效率很有必要。近年來，各種新的優化算法迅速發展，不少基于隨機搜索的現代優化算法取得了巨大成功。這些算法與傳統優化方法（如N-R算法）相比，在求解一些復雜的多維優化問題時具有一定的優勢。如粒子群算法和遺傳算法是基于隨機搜索的優化算法中比較成功的2種算法[2]。粒子群優化算法是通過模擬鳥群覓食行為而發展起來的1種基于群體協作的隨機搜索算法，搜索速度快、效率高，但在搜索全局最優解方面還有所欠缺；遺傳算法是1種借鑒生物界自然選擇和進化機制發展起來的高度并行、隨機、自適應搜索算法，已成功應用于組合優化、機器學習、工程優化等諸多領域[3～7]。

本文將遺傳算法應用于發動機穩態調節規律（或控制規律）的優化設計問題中，提出了1種發動機調節規律的設計方法，在考慮多種約束條件的情況下得到最優的發動機調節規律。

1 發動機調節規律

以混合排氣渦扇發動機調節規律為例，發動機的控制參數為主燃油流量Wf和噴管喉道面積A8[8]。發動機控制系統通過調整Wf使發動機的低壓轉子相對轉速n1、高壓轉子相對轉速n2和低壓渦輪后總溫T6（因高壓渦輪前總溫T4測量難以實現）的其中之一達到最大限制值，另外2個參數隨動，但不高于各自的限制值[9]。通過調整A8使發動機的低壓渦輪出口總壓P6與風扇進口總壓P1的比值EPR[10]符合要求的值。

發動機 n1、n2、T6和 EPR的調節規律分別如圖1、2所示。從圖1中可見，發動機調節規律根據不同的T1大致可分為4個區域。第1區域，當T1較低時低壓轉子相對換算轉速n1r達到限制值n1rmax，發動機進氣流量接近飛機進氣道的最大流量限制值；隨著T1的升高，n1rmax對應的n1逐漸升高，最終達到第2區域，即n1達到限制值n1max；隨著T1進一步升高，為保持n1=n1max，必須提高渦輪前總溫T4，T6隨T4的升高也逐漸升高，最終達到第3區域，即T6=T6max；當T1升高到某一溫度時，由于風扇和壓氣機存在“前重后輕”的現象，達到了第4區域，即n2達到了最大限制值n2max。

圖1 發動機轉速和排氣溫度調節規律

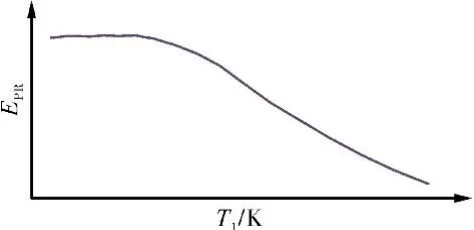
圖2 發動機EPR調節規律

在發動機工作的進氣溫度范圍內，控制器通過調節噴管喉道面積來實現要求的EPR控制。但是不同的EPR調節規律會影響發動機的n1、n2和T6，從而影響發動機在整個工作溫度范圍內的推力表現。如果考慮發動機加力工作狀態，則更為復雜，需要綜合考慮加力燃油流量Wfa與A8的匹配，以及余氣系數和加力燃燒室出口溫度的限制。因此在T1條件一定時，發動機的控制參數 Wf、Wfa、A8存在最優組合。

2 遺傳算法介紹

簡單遺傳算法的優化機理為：首先隨機生成初始種群，然后按照一定規則選擇優良的父代個體，再通過交叉和變異等操作生成子代。如此反復迭代，種群經過不斷進化，其平均適應度逐漸提高，最終得到最大適應度的個體[11]。然而隨著簡單遺傳算法的廣泛應用出現了局部收斂問題[12]。為了避免種群中個體出現局部收斂，衍生出了小生境遺傳算法。

在用遺傳算法求解多峰值函數的優化問題時，經常只能找到幾個最優解，甚至往往得到的是局部最優解[13]，小生境遺傳算法的基本目標就是形成和維持穩定的多樣性種群，在搜索空間的不同區域中并行搜索，最終實現多峰值問題的優化。De Jong[14]在1975年提出排擠機制的小生境實現方法。排擠機制的實現思想是：在種群中選取N個較優的個體組成排擠成員，然后依據新產生的成員與排擠成員的相似性來排擠掉一些與排擠成員相類似的個體。其中個體之間的相似性可用個體之間的距離來度量。隨著排擠過程的進行，群體中的個體逐漸被分類，形成各個小的生存環境，并維持群體的多樣性[14]，小生境遺傳算法的流程如圖3所示。

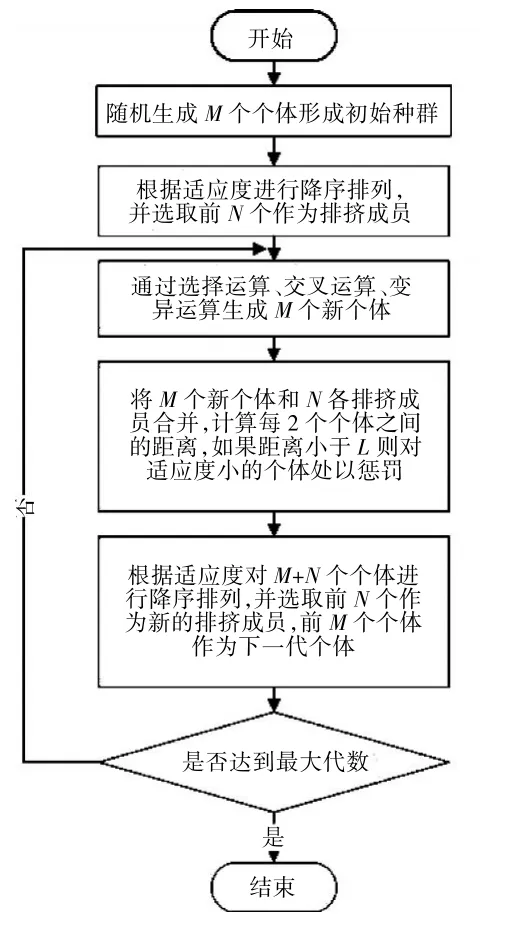
圖3 小生境遺傳算法流程

3 遺傳算法測試

在使用小生境遺傳算法進行發動機調節規律優化設計之前，先對該算法進行測試，并將測試結果與采用粒子群算法和簡單遺傳算法的計算結果進行對比。測試用目標函數見式（1），該函數在約束條件內共有16個局部最優點，其中有4個全局最優點。測試函數為

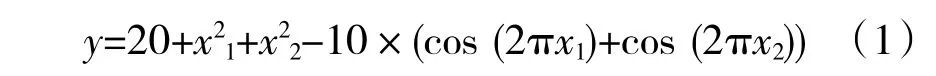
約束條件：xi∈[-2，2]（i=1，2）。

懲罰函數：Penalty=0，即如果某個體被懲罰，則其適應度直接設為0。

遺傳算法運行參數如下：

種群規模：種群規模的給定參考范圍為20～100[13]，為保持種群多樣性將種群規模設為100；

進化代數：一般進化代數選取范圍為100～1000[13]，為減少計算量暫設為100；

交叉概率：Pc=0.6；

變異概率：Pm=0.01。

遺傳算法編碼和遺傳算子如下：

個體編碼：浮點數編碼；

選擇算子：比例選擇算子；

交叉算子：鑒于編碼方式采用的是浮點數編碼，所以交叉采用算術交叉方式，對第t代的1對個體P1t、P2t進行算術交叉[11]，在[0，1]區間隨機生成 1 個數r，如果 r≤Pc，則個體 P1t、P2t按式（2）進行算術交叉，

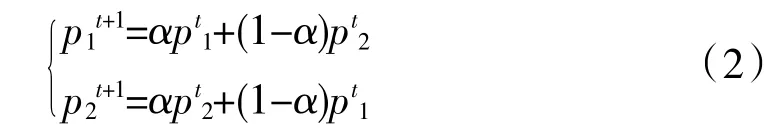
式中：α為[0，1]區間的數，本文將α設為0.5；

變異算子：采用均勻變異，假設1個個體X=（x1，x2），若 x1滿足變異條件，且 x1∈[x1min，x1max]，則在[0，1]區間隨機生成 1個數 r，x1變異后的新值 x1’=x1min+r·(x1max-x1min)。

粒子群算法、簡單遺傳算法和小生境遺傳算法的測試結果如圖4所示。從圖中可見，藍點的y值為個體的目標函數值，采用粒子群算法和簡單遺傳算法僅得到全局最優解和部分局部最優解。采用小生境遺傳算法能夠得到該函數的全局最優解和所有局部最優解，適用于優化發動機穩態控制規律這類復雜問題。種群在進化過程中平均適應度隨進化代數的變化如圖5所示。從圖中可見，隨著進化代數的增加種群平均適應度逐漸提高，當進化到某一階段時種群平均適應度保持在一定范圍內波動，表明遺傳算法收斂。采用簡單遺傳算法時種群進化到50代左右收斂，采用小生境遺傳算法時種群進化到30代左右收斂，并且30代以后的平均適應度變化較為平穩。

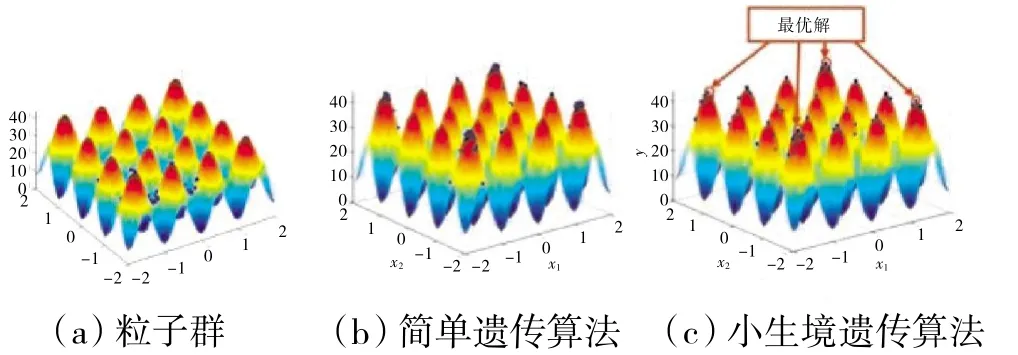
圖4 測試結果

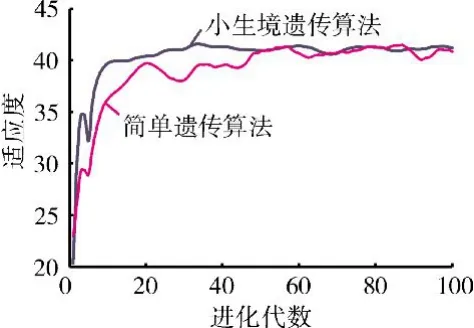
圖5 種群進化過程的平均適應度

4 遺傳算法參數選取

采用小生境遺傳算法能夠獲得優化目標的全局最優解和局部最優解，但是遺傳算法種群規模、變異概率和交叉概率的選取會影響遺傳算法的收斂速度，對于優化發動機穩態調節規律這類計算量龐大的問題，需要對種群規模、變異概率和交叉概率參數的選取進行分析和優化，以提高計算效率。

4.1 種群規模

種群規模表示1代中個體的數目，決定了每代優化的計算次數。一般總群規模選取范圍為20～100。為了找出計算量最小的種群，選取種群規模分別為20、30、40、50、……、100 的情況，每個種群規模計算10次，10次計算的進化代數取平均值表示該種群規模下的平均進化代數。每個種群規律條件下的平均進化代數如圖6所示。每個種群規模條件下的總計算次數（總計算次數=種群規模×進化代數）如圖7所示。從圖6、7中可見，種群規模為100時進化平均代數最小，為27代，但實際計算次數為2700次；種群規模為20時平均進化代數為30.5，但實際計算次數僅為612。因此種群規模為20時計算量最小。

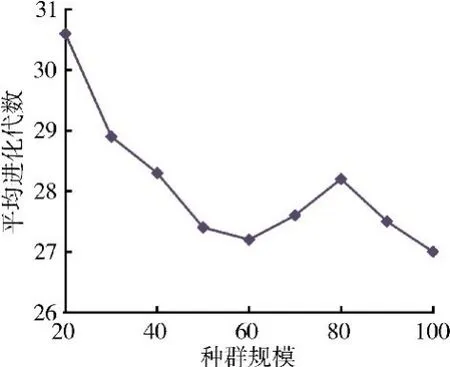
圖6 不同種群規模對進化代數的影響

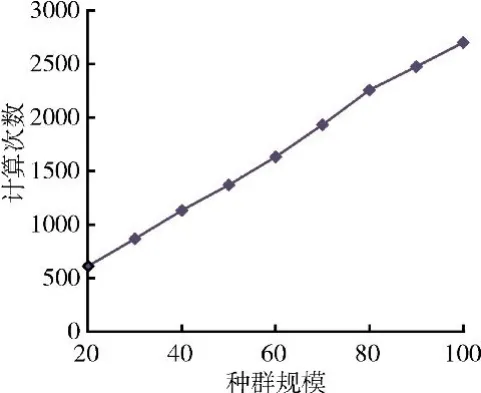
圖7 不同種群規模對計算次數的影響

4.2 交叉概率和變異概率選取

在遺傳算法中，交叉概率一般建議取值范圍為0.40～0.99，變異概率取值范圍為0.001～0.010[13]。為了找出合適的交叉概率和變異概率進行多次評估，結果見表1。從表中可見，交叉概率對進化代數影響不大，變異概率對進化代數有影響，變異用0.002和0.004，進化代數少。為了減少計算量，交叉概率設為0.80，變異概率設為0.004。

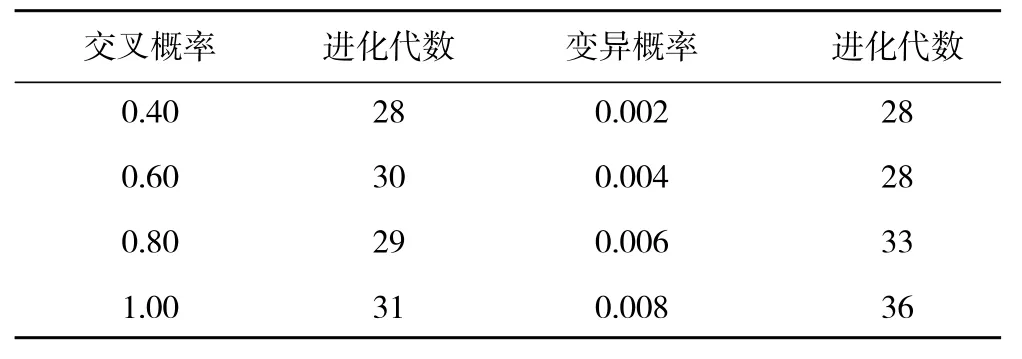
表1 不同交叉概率和變異概率測試結果

5 發動機調節規律的優化設計

將發動機穩態模型帶入小生境遺傳算法中，將其看作復雜的目標函數，并以獲得最大推力F為目標。該問題的模型為：

目標函數為max F=fengin（X），約束條件為：

高壓渦輪前溫度：T4≤T4max；

風扇裕度：ΔSMf≥ΔSMfmin；

壓氣機裕度：ΔSMc≥ΔSMcmin；

低壓相對轉速：n1≤n1max；

高壓相對轉速：n2≤n2max；

噴管喉道面積：A8min≤A8≤A8max

發動機進口換算流量：W1r≤W1rmax；

懲罰函數：Penalty=0。

在不加力的混合排氣渦扇發動機模型中共同工作方程共有29個方程組[15]，實際變量為31個，為了保證方程組具有惟一解，必須附加2個量，這2個量組成的向量便成為遺傳算法中的個體。對于發動機實際的工作情況是通過給定Wf來調節n1、n2和T6，通過給定A8調節EPR。根據本文采用的發動機模型，其計算輸入為n2和A8（n2可近似表征Wf），即遺傳算法中的個體可表達為 Xi=|n2，A8|。

發動機調節規律的優化設計結果如圖8、9所示，從圖中可見，發動機調節規律優化前后的主要區別在于發動機T6和n2受限制區域，在該區域n1優化后低于優化前的，而EPR優化后高于優化前的，對于混合排氣渦扇發動機來說，n1r決定發動機進口空氣流量，EPR決定發動機排氣速度。當T1較低時，發動機n1r或n1達到限制值，表明發動機進口空氣流量達到最大空氣流量，且發動機EPR達到了較優的狀態，因此該區優化前后的結果相近。

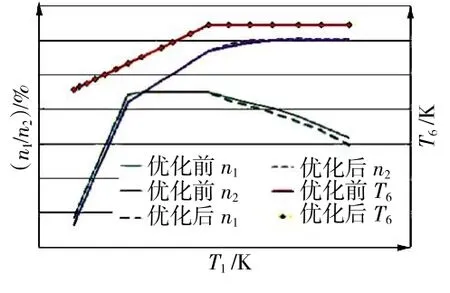
圖8 優化的轉速、溫度調節規律

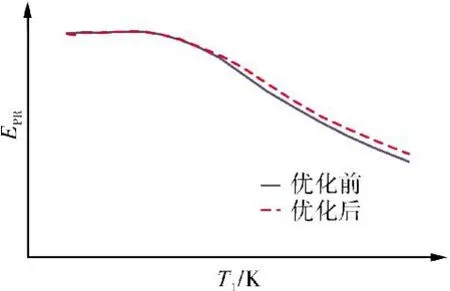
圖9 優化的EPR調節規律

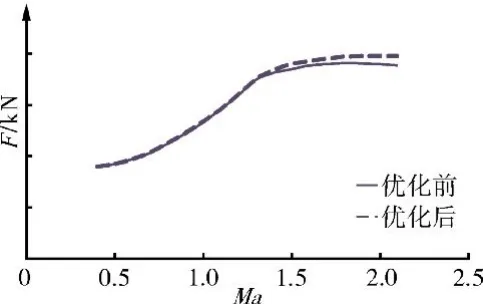
圖10 在H=11km時發動機的推力特性

當T1升高到T6和n2受限制區域時，發動機n1r和EPR是相互制約的2個量，比如提高n1r則需要放大A8，這樣會使發動機進口空氣流量提高，發動機推力有增大的趨勢；但是因A8增大導致EPR降低，影響了發動機排氣速度，發動機推力有減小的趨勢。所以n1r和EPR存在最優的匹配，同時反映出發動機控制參數Wf和A8存在最優匹配。因為發動機調節規律在進行優化設計前未充分考慮Wf和A8最優匹配的問題，因此在該區域的調節規律有一定的優化余地。

以H=11 km為例，發動機調節規律優化前后的速度特性對比如圖10所示。從圖中可見，在n1r和n1受限制區域，發動機采用優化前后的調節規律，推力表現相當；在T6和n2受限制區域，采用優化后的調節規律，發動機推力大。

在最大（全加力）狀態下的推力優化更為復雜。發動機模型中需設定的變量增加（加力燃油流量Wfa或加力出口總溫T7），對于最大狀態推力優化問題，個體表達為：Xi=|n2，A8，T7|。

目標函數為max F=fengin（X），約束條件在原基礎上增加：

加力燃燒室出口總溫：T7≤T4max；

加力燃燒室出口余氣系數：α≥αmin；

加力狀態噴口面積：A8a≤A8max。

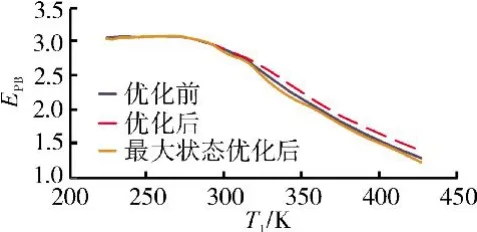
圖11 最大狀態EPR調節規律

在最大狀態優化過程中，發動機的 n1、n2、T6調節規律與中間狀態的一致。

最大狀態EPR調節規律如圖11所示。從圖中可見，優化結果比優化的中間狀態EPR調節規律低，與原EPR調節規律接近，表明在發動機加力工作條件下，為了能夠獲得更大的推力，需要將噴口放大，提高進氣流量。這樣在保證加力燃燒室余氣系數不低于要求值條件下，加入更多的燃油。由此可見，原EPR控制規律是為了獲得大的加力推力而設計的。優化的加力供油規律和加力推力比原狀態略高，如圖12、13所示。

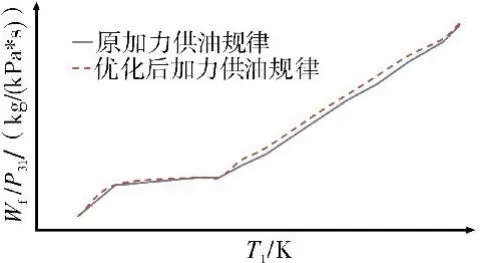
圖12 加力供油規律

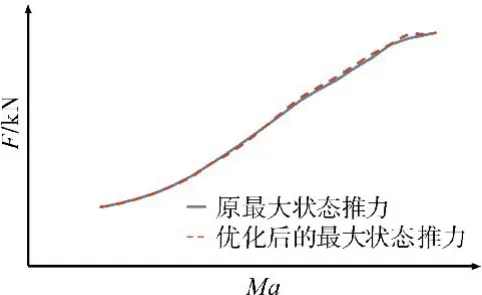
圖13 最大狀態推力

6 結論

（1）本文針對混合排氣渦扇發動機調節規律進行了分析，Wf主要用來調節發動機的 n1、n2和 T6，A8用來調節EPR，當發動機工作在中間狀態時，Wf和A8存在最優的組合，當發動機工作在加力狀態時，Wf、Wfa和A8存在最優的組合。根據優化結果發現，在發動機中間狀態下通過收小噴口能夠獲得較大的推力，在最大（或加力）狀態下可通過增大噴口同時提高加力供油的方式獲得較大的加力推力；

（2）介紹了1種基于排擠機制的小生境遺傳算法，并采用1種多峰值2變量的函數進行測試，測試結果表明，該遺傳算法能夠得到該測試函數的局部最優解和全局最優解；

（3）將發動機模型作為目標函數帶入小生境遺傳算法中，并給定一定的約束條件和懲罰機制，對遺傳算法參數進行優化，在種群規模為20、交叉概率為0.8、變異概率為0.004時，能夠使進化代數縮減到30以內，減少了優化過程的計算量，提高了效率；

（4）采用遺傳算法進行發動機調節規律的優化設計，擺脫了傳統的人工反復迭代的設計過程，提高了發動機調節規律的設計效率。