逆向噴流激波針減阻防熱特性

文/何天琦 羅世彬

（中南大學航空航天學院 湖南省長沙市 410083）

高超聲速飛行器是二十一世紀世界航空航天事業發展的一個主要方向，其具有飛行速度快、反應時間短、突防能力強等特點[1]，可以對遠距離目標進行直接打擊。在設計過程中，為了保證飛行器良好的飛行性能，外形一般設計為扁平尖銳形狀，同時由于空氣的黏性作用，物面邊界層內具有較大速度梯度的各層氣流產生強烈摩擦使壁面附近溫度升高，高溫高壓氣體通過殼體傳遞到內部，會導致電子電路運行穩定向變差，甚至會破壞飛行器結構[2]。因此，降低氣動阻力和氣動加熱始終是設計者所面臨的兩個主要問題，平衡好這兩者的關系對于高超聲速飛行器應用于工程實際具有重要的意義。一般來說，高超聲速飛行器的熱防護手段可分為主動冷卻和被動防護兩種[3-4]。被動防護方法通過使用耐熱材料或材料燒蝕達到隔熱冷卻的目的，防熱效果取決于材料的特性，當飛行器壁面熱流升高時，所需要的防熱材料就越厚，使飛機的整體質量增加，不利于機動性。主動冷卻方法主要分為三種：一是沿駐點線能量投放[5]，向前方來流中注入可燃物質、微波、激光等,這是一種主動流動控制技術； 二是逆向噴流技術[6-8]，是指向飛行器前緣流場注入冷卻介質，改變飛行器鈍頭體頭部的流場結構，將弓形激波向前推移，增加激波脫體距離，已達到降低熱流和氣動阻力的目的。三是激波針技術[9-11]，即在飛行器頭部設計特定的機械結構，改變鼻錐的繞流流場以實現防熱減阻的方法。目前，國內外學者分別對逆向噴流以及激波針技術進行了數值模擬研究以及實驗研究，黃偉等人[12]對逆向噴流及相關技術進行了較為詳細的綜述。Rong等人[13-14]使用氮氣作為噴流介質進行了數值仿真，得到了與實驗數據較為吻合的結果。激波針這一概念由Piland和Putland提出[15]。美國蘭利實驗室對安裝激波針的鈍頭體在高超聲速流場中進行了風洞實驗研究[16]。研究指出：安裝激波針的鈍頭體其阻力下降十分明顯。日本東京大學Shashank Khurana[17]將激波針應用于X-33簡化外形上并進行了風洞實驗，驗證了激波針的減阻防熱能力。目前該技術已經應用到了“三叉戟”I型等導彈的設計當中[18-19]。但激波針本身作為尖銳前緣結構，承受著劇烈的氣動加熱所以極易被燒蝕。隨著對高超聲速飛行器可重復使用性能要求的提出，單一的激波針結構已經很難滿足需求，為了使其實現可重復使用，文獻[20]提出了一種聯合激波針以及逆向射流的減阻防熱方法，通過數值模擬證明了該方法可以有效降低頭部熱流，并進一步降低外形阻力。文獻[21]在二維平面討論了噴流激波針的結構參數對弓形頭部的減阻防熱性能的影響。文獻[22]研究發現噴流激波針的結構參數與其減阻性能之間具有較強的非線性規律。耿湘人[23]等人通過數值模擬的方法對比了逆向噴流對二維圓柱和三維軸對稱球頭的減阻降熱效果，發現兩種模型在肩部再附區的流動特性區別較大，在球頭外形的流場中斜激波會再附在鈍體肩部與主激波形成激波，產生局部“熱斑”。另外，本文作者在文獻[24]中分析了隨著攻角的增加，肩部的熱環境會更加惡化的現象。因此，本文將針對三維外形肩部熱斑問題進行進一步討論，并探索降低阻力和熱流的方法。

1 數值方法

1.1 計算方法

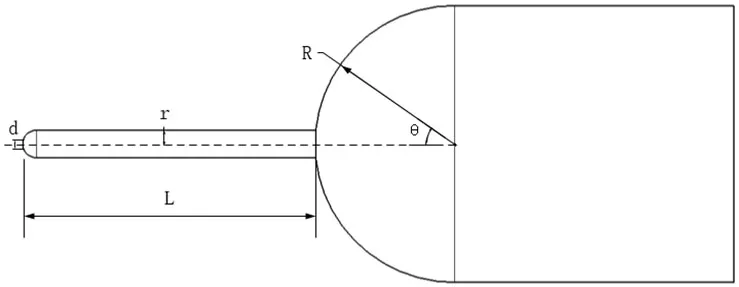
圖1：帶逆向噴流激波針的外形示意圖

圖2：激波針流場圖與風洞試驗紋影圖

連續介質的流體力學控制方程是三維Navier-Stokes方程組，選擇理想氣體狀態方程來模擬真實氣體性質，并且不考慮徹體力和熱源。空間離散采用AUSM格式，時間離散采用LU-SGS格式的隱式迭代法求解加快收斂速度[25-26]。本文所采用的湍流模型為Menter[27]提出的剪切應力輸運模型（Shear-Stress Transport-Model），另外文獻[21]通過數值模擬與實驗數據進行對比，得出SST（k-omega）湍流模型可以更好地模擬逆向射流的流場。

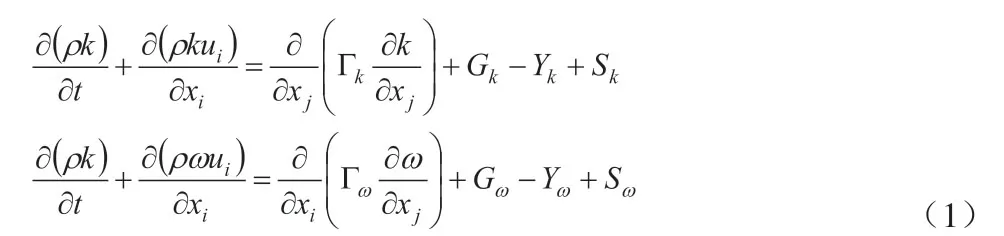
1.2 計算模型

基準模型采用較常見的軸對稱旋成體球柱外形，球頭半徑R為7.5mm，噴流激波針半徑r為0.75mm，本文為了分析噴流激波針長度對其減阻防熱性能的影響，因此選取激波針長度L為L/R=1～4，球頭直徑D與噴管出口直徑d的比值為31.5。其外形示意圖如圖1所示。

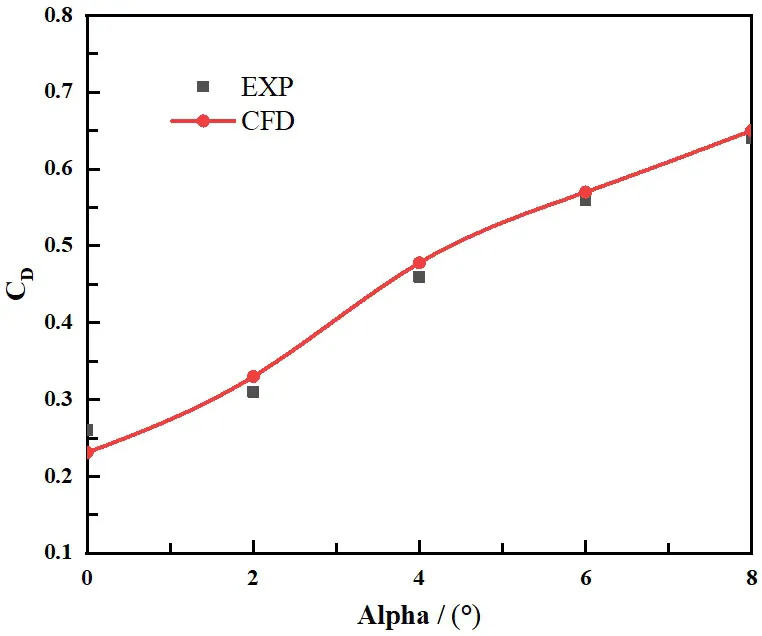
圖3：阻力系數隨攻角變化

圖4：逆向噴流實驗模型

圖5：計算網格

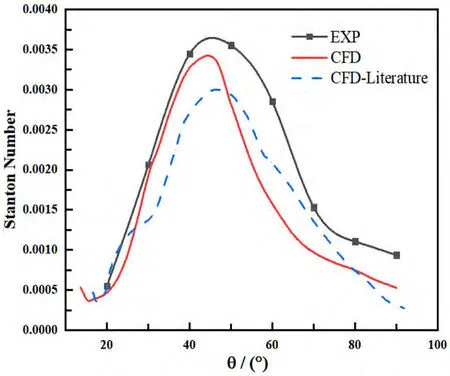
圖6：鈍頭體母線斯坦頓數分布

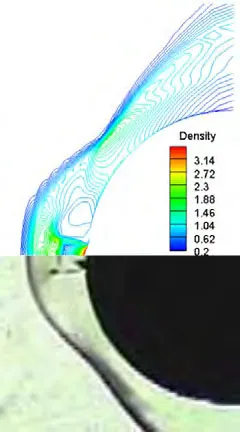
圖7：數值模擬密度云圖與實驗紋影圖

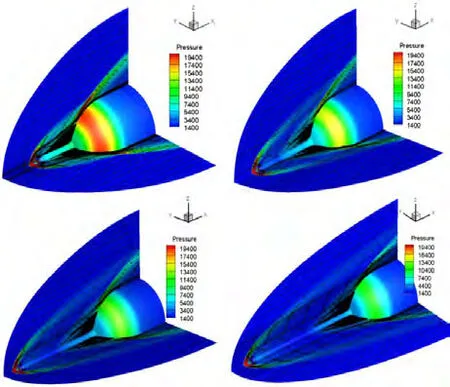
圖8：靜壓云圖與流線對比圖

1.3 邊界條件

算例的來流條件取 =6，=1400.9 Pa，=225.47 K，計算中認為壁面無滑移，并且使用了等溫壁邊界條件Tw=300 K。噴管邊界條件為壓力入口，噴流出口馬赫數為1，噴流總壓與來流總壓比Pr為0.1～0.4。

2 驗證與確認

本文將分別通過對激波針與逆向射流流場進行數值模擬與風洞實驗數據結果進行對比，來驗證本文數值方法的正確性與可信性。

算例一激波針模型來自于文獻[28]，鈍頭體球頭半徑R=50mm，激波針長度L=200mm，激波針半徑r=5mm，驗證算例的邊界條件為：來流馬赫數 =6，攻角0～8度。數值模擬流場圖與風洞實驗紋影對比如圖2所示。不同攻角下的阻力系數與實驗數據對比如圖3所示。由圖可知，仿真結果與試驗數據在數值和趨勢上基本吻合。

算例二采用鈍頭體逆向噴流進行數值模擬來驗證本文數值方法對逆向噴流仿真結果的可信性。實驗模型來自于文獻[29]。實驗模型與計算網格如圖4和圖5所示。來流馬赫數為3.98，總壓為1.37MPa，溫度為95.25K，逆向噴流馬赫數為1，噴流總壓與來流總壓比為0.6，噴流總溫為300K。

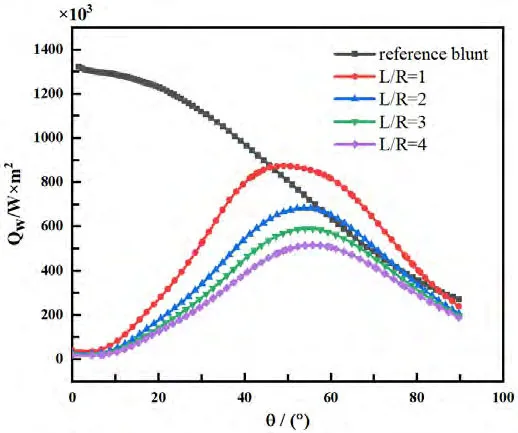
圖9：鈍頭體母線壁面熱流分布

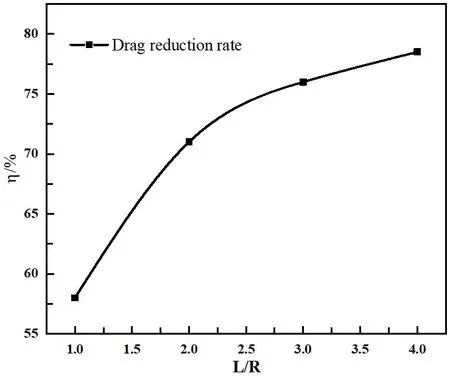
圖10：減阻率隨L/R變化

算例結果采用斯坦頓數（St）與流場密度分布云圖與實驗結果進行對比，由圖6可知，數值模擬與文獻和實驗得到的結果變化趨勢基本一致，熱流峰值的位置基本相同，在回流區下游數值模擬與實驗結果存在一定誤差可能是由于兩者采用的冷卻氣體不同以及物理模型系數不同造成的。

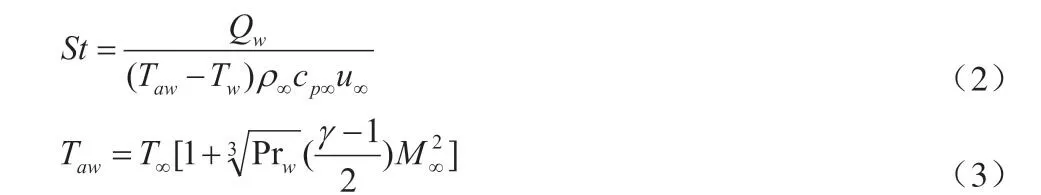
數值模擬的密度云圖如圖7所示,圖中馬赫盤以及激波的位置吻合度較好，馬赫盤清晰可見，分離激波較為明顯。由以上兩算例可以證明本文數值模擬方法的正確性以及可信度。

3 數值模擬結果及分析

為使噴流激波針得到更優的減阻防熱性能，本文將討論噴流激波針長度以及噴流壓比對其減阻防熱效果的影響，并分析其變化與鈍頭體肩部熱斑的關系。

3.1 噴流激波針長度影響分析

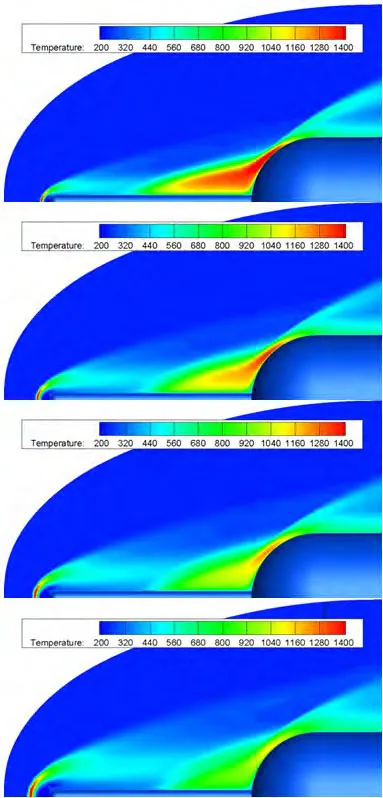
圖11：對稱面溫度分布

本文選取噴流激波針長度L/R=1～4進行數值模擬，圖8給出了帶不同長度噴流激波針鈍頭體在流場中的壓力云圖以及流線分布。從圖中可以看出當噴流激波針較短時，斜激波再附在鈍頭體肩部，產生高壓區，隨著激波針長度增加，鈍頭體壁面壓力逐漸降低，且壁面壓強分布更加均勻，當L/R 3時，斜激波在鈍頭體表面幾乎沒有附著。

鈍頭體壁面熱流分布以及減阻率η隨噴流激波針長度變化關系如圖9、10所示。其中：

CDi為帶噴流激波針鈍頭體的阻力系數，CD1為不帶噴流激波針鈍頭體阻力系數。

從圖9可以看出不同長度的激波針對駐點區域的防熱能力都比較明顯，隨著噴流激波針長度的增長，熱流峰值逐漸減低，且熱流峰值位置向后移動，當L/R≥3時，肩部熱流已經低于基準鈍頭體，熱斑問題基本得到了改善。

由圖10可知，噴流激波針的減阻能力也隨其長度的增加而增長，但是可以看出當L/R超過3時，減阻率的增長趨勢明顯減弱，隨著激波針長度的進一步增加，其減阻能力會達到飽和，反而會對其結構強度提出更高的要求。

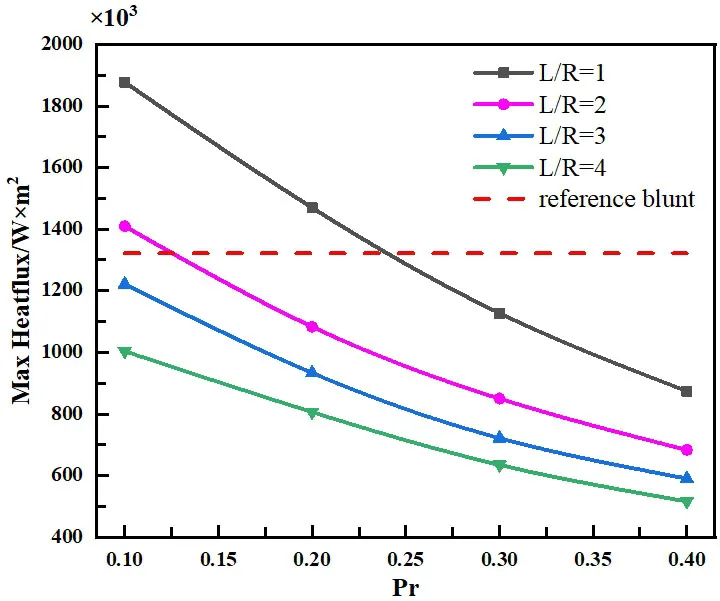
圖12：壁面熱流峰值隨噴流壓比變化

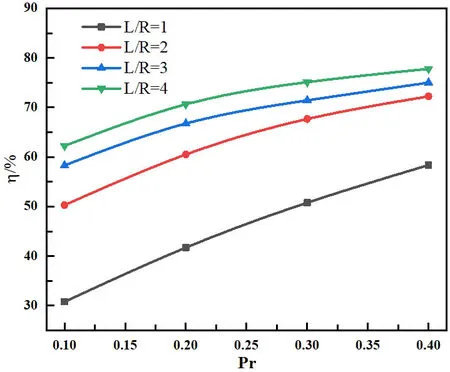
圖13：減阻率隨噴流壓比變化

3.2 噴流激波針噴流壓比影響分析

本小節討論逆向噴流壓比對噴流激波針減阻防熱性能的影響，選取噴流壓比為0.1～0.4。圖11給出了噴流激波針長度為L/R=3時，噴流壓比分別為0.1,0.2,0.3,0.4時的對稱面溫度云圖，從圖中可以看出，噴流壓比越大，脫體激波面形成的位置距離頭部越遠，激波針頭部低溫區面積不斷擴大將整個噴流激波針頭部包裹，改善了頭部的熱環境。另外，鈍頭體肩部附近高溫區面積逐漸減小，使壁面溫度梯度變緩，有利于提高噴流激波針的防熱性能，改善鈍頭體肩部熱斑問題。

四種長度噴流激波針鈍頭體的壁面熱流峰值隨噴流壓比變化如圖12所示。從圖中可以看出，增加逆向噴流壓比有利于降低壁面熱流，隨著噴流壓比的進一步增長，壁面熱流下降的趨勢減弱。另外，可以看出在噴流激波針長度較短時，增加噴流壓比對其防熱能力的提高更加明顯。

圖13給出了噴流激波針減阻率隨噴流壓比變化的關系，從圖中可以看出，噴流激波針的減阻能力隨噴流壓比的增加而增加，隨著壓比的增長減阻能力逐漸達到飽和，另外可以看出，在激波針長度較短時，改變噴流壓比對減阻效果的影響更加明顯，這與在防熱方面得到的結論相符。

4 結論

本文通過數值模擬的方法分析了噴流激波針長度與噴流壓比對其減阻防熱性能的影響，得出以下結論：

（1）當L/R≤2時，鈍頭體肩部激波干擾較為明顯，隨著激波針長度增加，鈍頭體壁面壓力逐漸降低，且壁面壓強分布更加均勻，其減阻能力增強，但L/R超過3時，這種趨勢會減弱，進一步增加其長度可能會產生負面影響。

（2）不同長度的激波針對駐點區域的防熱能力都比較明顯，隨著噴流激波針長度的增長，壁面熱流峰值逐漸減低，當L/R≥3時，肩部熱流已經低于基準鈍頭體，熱斑問題基本得到了改善。

（3）隨噴流壓比的增長，脫體激波遠離鈍頭體駐點，激波針頭部低溫區面積不斷擴大將整個噴流激波針頭部包裹，改善了頭部的熱環境。同時,鈍頭體肩部附近高溫區面積逐漸減小，壁面溫度梯度變緩，有利于提高噴流激波針的防熱性能，改善鈍頭體肩部熱斑問題。

（4）增加逆向噴流壓比有利于降低壁面熱流，隨著噴流壓比的進一步增長，壁面熱流下降的趨勢以及減阻能力減弱。另外，在噴流激波針長度較短時，增加噴流壓比對其減阻防熱能力的提高更加明顯。