基于二進離散小波
——核降噪自編碼的電機振動信號多級降噪

喻 卓,王 志,孫仲平,雷文鋒,于明誠,李 莉,訾一鳴,黨雨萌,黨亞固*

(1.四川大學 化學工程學院,四川成都 610065;2.四川華西綠舍建材有限公司,四川 成都 610000)

機械信號處理從20世紀60年代開始，早期主要通過對振動信號進行變換如傅里葉變換[1]，以獲取相應的時頻譜圖，從而進行時域分析頻域分析，如王志剛[2]等提出的通過共振調節提取信息，隨后小波變化及其變形在時頻信號處理的優異性[3]，David[4]提出的基于軟閥值降噪，Chang S G[5]等人提出自適應的數據驅動閾值降噪，之后如奇異值分解[6]、經驗模態分解(EMD)[7]、集總平均經驗模態分解(EEMD)[8-9]，隨著近年機器學習的應用基于自編碼[10]的降噪發展迅速。2008年Pascal Vincent[11]等人表明自編碼器可用于特征提取。2010年Vincent[12]等人提出棧式去噪自編碼器。

本文提出基于二進離散小波--核降噪自編碼的多級降噪模型，并將該模型應用于多維振動信號降噪方面。對采集的振動數據利用二進離散小波局部變換，通過濾波器對每個特征集分別進行降噪，將降噪后的數據通過核方法映射到高維空間，利用降維自編碼算法對高維空間數據進行全局處理，進而映射到低維空間，達到保留主要有效信號除去干擾噪音信號的效果。

1 模型原理

1.1 二進離散小波變換

圖1 二進離散小波降噪流程圖Fig.1 deniose of discrete dyadic wavelet transform

小波變化可以更加精準地對時序頻域進行局部信號表征[13]。小波變換常見的形式有連續小波變換(CWT)、離散小波變換(DWT)等，在信號的時域分解中，常用二進制離散小波變換(DDWT)。

對于二進制離散小波降噪，其小波基、分解層數，閾值等都是影響最終去噪效果的關鍵因素。本文利用如圖1流程進行最優參數選擇。

1.1.1 小波基最大分解層數的選擇

主要的小波基函數包括有haar、dbN、coifN、symlet、meyer小波[16]。選擇小波基的指標要求有：支撐長度、正交性、正則性、高階消失矩。相關性質如表 1。

表1 小波基函數性質匯總表Table 1 properties of mother wavelet table

綜合上表性質，可選的基函數有：haar、dbN、coif N、symN四類。參考文獻[16-17]可以知道，Haar小波在時域上是不連續的，所以不適合作為基小波。Symlet小波函數是Daubechies針對dbN缺陷提出的改進版。symN小波除了具備db小波的優勢外還具有更好的對稱性，即一定程度上能夠減少對信號進行分析和重構時的相位失真。Coiflet小波同樣由Daubechies構造，與dbN相比coif N小波具有更好的對稱性。因此文章后面的二進離散小波中將選擇選擇coifN和symN小波函數進行比較說明。

由文獻[18]知最大分解層數與小波函數的階數成階梯下降的趨勢，與采樣頻率成正比，即當采樣頻率和小波基函數確定，其通用最大分解層次也隨之確定。

1.1.2 閥值選擇

閥值的選擇基于模型[19]y=f(t)+e ，可以通過小波系數來評估能夠消除噪音的小波域的閥值，目前常用的閥值選擇方法有，固定閾值估計、極值閾值估計、無偏似然估計以及啟發式估計。其中固定閥值降噪效果明顯[20]。本文基于Stein的風險無偏估計軟原理設計通用閥值 。

通過上述方法計算出閥值 ，再在該數值尺度上 ，其中 為單位尺度值。最后通過窮舉組合小波函數、閥值。并以信噪比和樣本標準差作為參考標準選擇最優參數。

1.2 核自編碼

1.2.1 核函數

Cover定理[14]指出，對于在歐式空間中一般位置上的n個點，將它們非線性地投射到高維空間會比投射到低維空間更可能是線性可分的，并且維數越高，這種可能性越大。

因此通過核方法將原始樣本非線性映射到再生核希爾伯特空間，然后在該空間進行特征壓縮關聯。在這個過程過中先驗知識通過核函數和參數的選擇耦合到降噪自編碼的分析過程中，從而能夠更有效地分析出數據的本質結構[21]。

常見的核函數有：線性、多項式、高斯徑向、sigmoid核函數，這些核函數的公式較為常見可參考文獻[6-7]，高斯徑向核采用歐氏距離作為距離函數，進行變換的矩陣具有好的正定性，其核函數僅有一個參數，模型復雜度較低且可以滿足特征的非線性映射；而且徑向基核在計算上沒有數值困難。因此在本文中選擇高斯徑向核函數作為模型的核函數。

1.2.2 核自編碼

高維數據可以通過一個多層神經網絡把它編碼成一個低維數據，從而重建這個高維數據，這個神經網絡的中間層神經元數是較少的，可把這種神經網絡叫做自動編碼網絡(Auto-Encoder,AE)[9-10]。

核降噪自編碼包含三個網絡層次，分別為核函數映射層、自編碼器編碼層、自編碼器解碼層。其模型如圖2。

圖2 核自編碼網絡模型Fig.2 kernel methodwihdenoising autoencodernetwork model

核映射層：將粗過濾的信號數據通過核方法映射到高維空間，對于輸入數據x=(x1,x2,...,xn)，使用高斯徑向核函數作為映射核函數，因此核函數映射層可以表示為：

編碼層：將核函數映射層的輸出作為該層的輸入，考慮到實際應用的復雜性，為了進一步優化模型提高模型的泛化能力，需要為自編碼器加入滿足正態分布的白噪音進一步提高模型的擬合能力，以提高模型的適用性其次這里我們加入高斯白噪音[22]，得到混合噪音數據的輸入為：

說明：利用awgy函數來添加高斯白噪音，其中SNR表示信噪比。

因此該層可以表示為：

其中：f(t)是Sigmoid函數激活函數，W為權值矩陣，b為偏置向量。

解碼層：編碼層的輸出為解碼層的輸入，解碼層的作用在于重構出核函數的映射過程，該層可以表示為

其中：g(t)為解碼層激活函數，一般與f(t)相同， W′ 為解碼層權值矩陣，b′ 為前置向量。

優化過程：通過最小化重構誤差來同時優化編碼層和解碼層，從而學習得到針對樣本輸入 的抽象特征表示y′ 。編碼器通過優化參數集θ={w,w′ b,b′ }使得重構誤差最小，為了求解方便，設定w′ =(w)T。

本文考慮到以均方誤差作為損失函數對復雜振動信號的特征學習魯棒性低，最大相關熵損失函數對復雜非平穩背景噪音不敏感等特性，根據文獻[23]的描述選擇最大相關熵函數作為模型的損失函數。因此代價函數可以寫為：

為構造結構分析模型，在上文的代價函數中加入懲罰因子，以滿足結構風險最小。

添加L2正則項作為懲罰因子，在每次的優化過程中，可以使得權值盡可能小，最后構造一個權值較小的模型[7]。

此時的懲罰函數為：

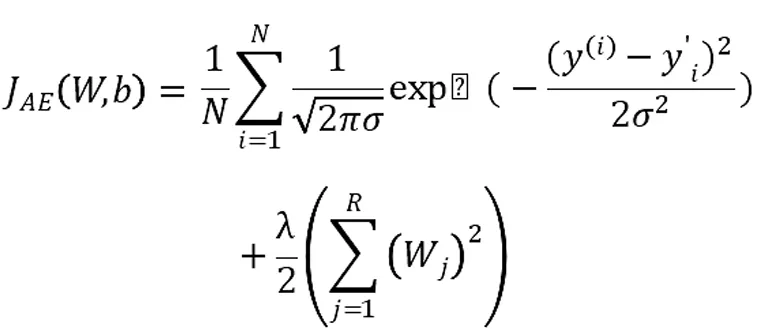
其中：λ為懲罰系數，λ≥0 。N是樣本數，R是特征數。

利用梯度下降算法計算收斂參數，分別對W，b求偏導：

其中， δi為每個單元的殘差，aj為每個單元的激活值，利用前向算法和后向算法就可以求出每個單元的激活值和殘差。從而可以得到權值矩陣和偏置向量。

1.4 二級降噪模型

二級降噪模型總體可分別為五個大板塊：振動信號的粗過濾、數據預處理、核降噪自編碼模型訓練、模型調參、降噪測試。

圖3 多級降噪模型流程圖Fig.3 multi-level denoise ofmodelflow

step1：選擇合適的小波函數并計算閥值，將信號進行二進離散小波分解、噪聲過濾、信號小波重構等幾個步驟實現對信號特征的提取。

step2：使用核函數實現特征低維向高維的映射，便于在高維空間提取特征間的相關信息。

step3：數據標準化處理，考慮到降噪自編碼使用的是Sigmoid函數這里我們對數據集進行歸一化處理。

step4：確定降噪自編碼的網絡結構，根據輸入數據維數確定輸入層神經元數，確定隱藏層層數，確定隱藏層各層的神經元數。

step5：向數據集中加入前期選定的白噪音。

step6：模型訓練階段設置模型參數，包括權重、學習率、誤差閥值等，計算模型的代價函數，判斷誤差是否在設置的閥值之內或者達到設定的迭代次數，不然重復上述過程進行更新迭代，直到達到要求，最終確定模型。

2 實驗分析

實驗設備參數：Rexnord ZA-2115雙列軸承，滾子直徑8.407mm，采樣頻率20KHz，數據長度為20480點。數據集來源美國國家儀器實驗室VIEW計劃公開數據。

根據文獻[15]介紹，使用小波濾波器檢測機械脈沖狀缺陷信號的弱信號。基于上文2.1的理論描述，構建二進離散小波過濾模型對數據集進行處理，得到的結果如下表2,3。

表2 coifN小波基-閥值信噪比表Table 2 coifNof mother wavelet threshold SNR table

表3 symN小波基-閥值信噪比表Table 3 symNof mother wavelet threshold SNR table

從表中分布可以知道，coifN小波函數和symN小波函數過濾降噪的區別不大，因此本文僅做symN小波函數-閥值與信噪比和樣本標準差圖如下圖4，圖5。

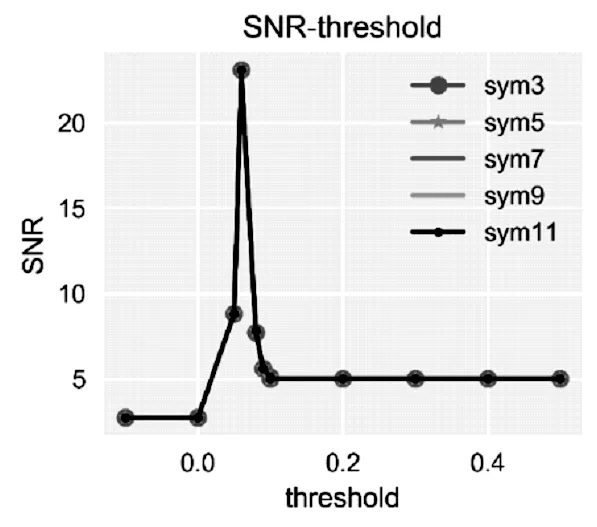
圖4 小波基函數-閥值信噪比Fig.4 amother wavelet threshold SNR

圖5 小波基函數-閥值樣本標準差Fig.5 bmother wavelet threshold sample-standard-deviation

根據圖4,圖5，可知在閥值為0.06時得到的信噪比最高，其次通過降噪可以降低信號數據的波動情況，因此該閥值下的樣本標準差同樣滿足小于原始數據的樣本標準差。考慮到支撐長度因素，小波函數的支撐長度為5～9之間，故本文選擇sym5小波基作為二進離散小波降噪的基函數。

綜上對于二進離散小波過濾降噪而言，本文選擇的基小波為sym5，根基算法得到的最大分解層數為11層，選用的閥值為0.06。得到的降噪效果如圖6：

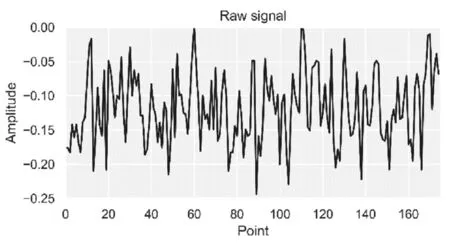
圖6 二進離散小波降噪前Fig.6 before discrete dyadic wavelet transform take denoise

圖7 二進離散小波降噪后Fig.7 bafterdiscrete dyadic wavelet transform take denoise

為了進一步顯示降噪效果，利用二進離散小波降噪的數據與原始數據集構建誤差函數，計算測試集中所有數據點的重建損耗，利用重建損耗的時序分布來確定降噪后數據的有效性。如圖8。

圖8 二進離散小波降噪后損耗圖Fig.8 loss of after discrete dyadic wavelet transform take denoise

從圖8可以看到進過小波降噪后數據與原始數據損耗的范圍為0～0.06，且損耗的時序分布波動較大，對全局時序而言，任然存在較大的振動波動，即通過小波降噪后的數據存在整體噪音的缺陷。

最后對二進離散小波處理后的數據集，加入兩次加入高斯白噪音，搭建自編碼模型，進行模型訓練，本文使用四層神經網絡，其中輸入層第一層節點核變換后的特征數K，第二層有20個節點，第三層有8個節點，第四層K個，使用最大相關熵作為損失函數，進行模型訓練模型。在每次模型訓練之后使用訓練數據的5%進行驗證。

模型的訓練效果如圖9，從圖可以看出，對上述設計的四層降噪自編碼模型而言，模型的迭代次數達到13時，改模型的訓練誤差和測試誤差均接近0.0016。

圖9 降噪自編碼訓練誤差-測試誤差-迭代次數Fig.9 training error-test error-times of denoising autoencoder

通過計算降噪后的信噪比，特征樣本標準差，其中比較項為：二進離散小波降噪后數據與降噪自編碼降噪后數據：

表4 多級降噪信噪比-樣本標準差Table 4 SNR sample-standard-deviation of multi-level denoise table

最后構建多級降噪之后的數據集與原始數據集的時頻點重建損耗曲線圖10。

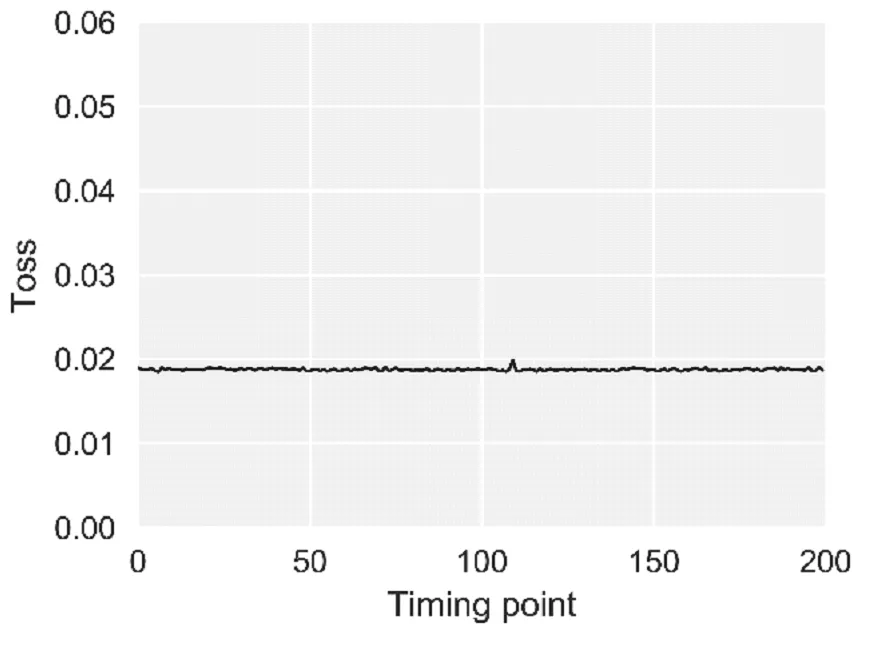
圖10 多級降噪損耗時序圖Fig.10 loss sequence of multi-level denoise

通過核降噪自編碼的全局降噪后，各特征信噪比均有不同程度的提高，提高范圍為18～38，同時與二進離散小波降噪處理后數據相比，數據樣本標準差降低2～3個數量級，說明信號的平滑性得到了大幅度優化，這點可以從重構損耗的時序曲線得到佐證，比較圖8和圖10可以明顯得到進過核降噪自編碼處理后的信號數據在損耗隨時間變換幅值波動微弱，且有明顯的平滑性。

4 結果與討論

本文對電機振動信號的降噪進行了研究，提出來一種結合小波信號處理和深度學習全局優化的多級降噪模型。該模型選擇sym5小波基作為分解基波，通過模型自動識別輸入信號的特征數與信號的長短，結合窮舉算法自動計算出小波降噪閥值，實現了二進離散小波降噪的自動化進程。文章通過將在核變換結合到降噪自編碼算法中并作為該算法的第一層變換函數，提出了四層變化的降噪神經網絡，將二進離散小波降噪后的數據作為該過程的輸入數據集，配合已經訓練好的神經網絡，可以直接得到進一步的降噪數據。因此本文的降噪模型在工程應用上具有非常強的自動化能力，能夠快速將采集的振動信號進行分解降噪，為實現設備的在線診斷提供有效的解決方法。

在降噪效果方面，文章所提模型的兩級降噪信噪比分別為23，和大于等于17；在信號的波動性方面，信號的樣本標準差由一級降噪的1.4×10-2(最大值)降到二級降噪的0.04×10-2。這也證明的改模型在處理多維振動信號降噪的有效性。