基于遺傳算法的改進K-means算法

文/林龍成

（江蘇省南通衛生高等職業技術學校 江蘇省南通市 226010）

K-means算法[1][2][3]是一種廣泛使用的聚類算法，思想簡單易行，時間復雜度接近線性，對大數據集，具有高效性和可伸縮性。但是算法也有一些局限性，需事先給定聚類數k 值；對于初始值的選擇比較敏感，選擇不同的初始值，可能會導致不同的分類結果。

遺傳算法[4][5]被廣泛應用于提高人工智能技術的性能。結合遺傳算法能夠尋找全局最優解的優勢，以及K-means 算法容易因為初始聚類中心的選擇不同而陷入局部最優解的問題，本文利用遺傳算法初始化K-means的初始聚類中心點，提出基于遺傳算法的K-means聚類算法GA-K-means。

1 K-means聚類算法

K-means 算法，也被稱為k-均值算法，是基于距離的聚類算法，采用距離作為相似性的評價指標，兩個數據點的距離越近，則相似度越大。計算樣本間的距離公式有歐氏距離、曼哈頓距離、余弦相似度等，其中最常用的是歐氏距離。

K-means 算法基本思想是通過迭代將數據集劃分為不同的類簇，使得用不同類簇的均值來代表相應各類樣本中心時所得的總體方差最小。誤差平方和準則函數公式為：

E 表示樣本空間中所有數據點到聚類中的平方誤差的總和。p表示數據對象，Ci表示第i 個類簇，mi表示第i 個類簇的平均值。

2 基于遺傳算法的K-means算法

2.1 GA-K-means算法的具體流程

GA-K-means 是在K-means 聚類中利用遺傳算法選擇最優的初始種子。圖1 為GA-K-means 聚類的總體框架。

首先，系統生成初始種群，用于尋找全局最優初始種子，遺傳算法對當前種群進行選擇、交叉和變異等遺傳操作，不斷更新種群，直到滿足停止條件；然后根據輸出的初始聚類中心，使用K-means算法進行聚類，輸出聚類結果。

2.2 染色體編碼

以學習風格為例，本文采用實數編碼方式，能夠直接反映問題的固有結構，便于設計專門的遺傳算子，緩解“組合爆炸”的問題。染色體的結構如表1 所示，前4 位表示第一聚類中心的學習風格向量，依次類推。

2.3 適應度函數設計

表1：染色體編碼

表2：10 次實驗結果

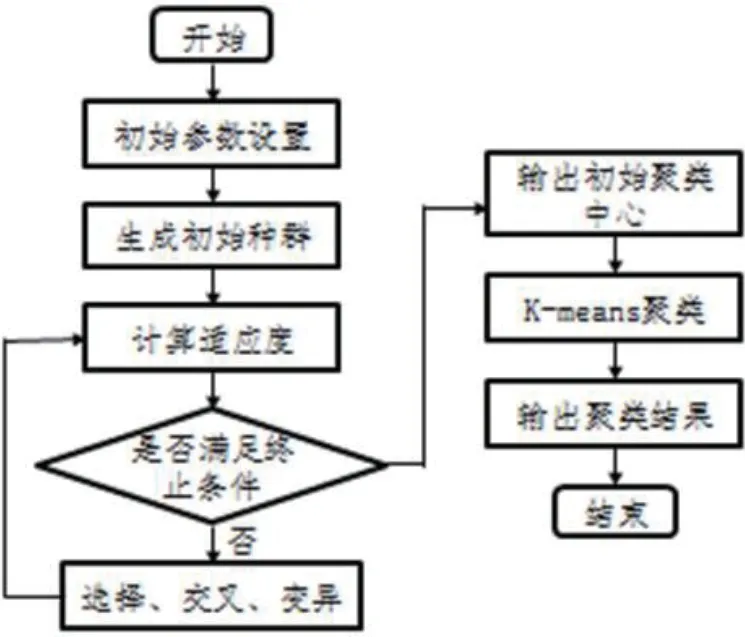
圖1：GA-K-means 算法

圖2：單點交叉

圖3：變異操作

適應度函數是促使遺傳算法收斂到最優解的一個因素。我們選擇總最小距離函數作為染色體強度的適應度函數，以找到K-means算法的最優初始種子。適應度函數定義如下：

其中，Gi表示第i 個聚類，Lj 表示屬于Gi的學習者，LSj表示第j 個學習者Lj的學習風格向量，gj表示Gj 的聚類中心。適應度函數Fit 越小，說明初始聚類中心的選擇越好.

2.4 遺傳算子

圖4：兩種算法的聚類結果

在遺傳算法中，通過一些列算子來決定子代的生成，本文使用選擇、交叉、變異算子，交叉算子通過雙親染色體交換有意義的遺傳物質來產生兩個新的后代，變異算子通過向種群中引入一個全新的成員來維持種群的遺傳多樣性。

2.4.1 選擇算子

選擇操作通過適應度選擇優質個體，拋棄劣質個體，體現了“適者生存”的生物法則。常見的選擇操作主要有：輪盤賭選擇、排序選擇、最優個體保存及隨機聯賽選擇。本文采用輪盤賭選擇方式，某染色體被選的概率Pc 為：

其中：f(xi)表示第i 個染色體的適應度值；∑f(xi)表示種群中所有染色體適應度值之和。

2.4.2 交叉算子

交叉是指兩個染色體按照某種方式交換部分基因信息，從而產生兩個新的染色體。常用的交叉方法有：單點交叉、雙點交叉、均勻交叉及算術交叉。本文使用單點交叉，從其中可能的三個交叉點P1、P2、P3、P4中隨機選擇一個交叉點。交叉操作如圖2 所示，其中P2 是所選交叉點。

2.4.3 變異算子

變異是指以一定概率隨機改變染色體編碼串中部分基因值，形成新的個體。常用的變異方法有：基本位變異、均勻變異、二元變異及高斯變異。本文采用基本位變異方法，從五種可能性（I 到V）中選擇一個隨機基因組（四位），并根據學習風格情境，使用相反選擇答案得到的4 位編碼串替換它。變異操作如圖3 所示，IV 基因被反向基因組（7 8 10 6）替換。

2.5 K-means聚類

（1）以遺傳算法得到的最優解作為初始聚類中心

（2）計算所有數據對象到這k 個初始聚類中心的距離，并將數據劃歸到離其最近的那個中心所在的類

（3）重新計算已經得到的各個簇的質心，作為新的聚類中心

（4）計算公式（1）中的準則函數E，若E 不滿足，重復第2、3 步，直到聚類的中心不再移動，輸出聚類結果

3 實證分析

為了檢驗本文提出的算法的有效性及對學生學習風格進行分析，本文使用MATLAB 進行仿真實驗，實驗環境的硬件配置為 Inter(R)Core(TM)i5-3470 CPU@3.20GHz 4.00GB，開發環境為 MATLAB R2016a。

下面采用傳統K-means 和GA-K-means 分別對學習風格數據進行分類，驗證本文提出的GA-K-means 算法的有效性。實驗結果如圖4 所示。

可以看出，傳統K-means 算法雖然收斂速度快，但是容易陷入局部最優解，而本文提出的GA-K-means 算法則能夠避免早熟現象，且收斂平穩，收斂效果明顯優于傳統K-means 算法。

為了進一步驗證算法的有效性，對傳統K-means 算法和本文提出的GA-K-means 算法分別進行10 次實驗，實驗結果如表2 所示。其中匹配度計算公式為：

從表2 可以看出，由于傳統K-means 算法對初始聚類中心的選擇比較敏感，導致每次聚類結果都有很大差異，10 次實驗結果的匹配度較低，而本文提出的GA-K-means 算法匹配度較高，具有較好的穩定性。

4 結論

本文在傳統K-means 算法的基礎上，提出了基于遺傳算法的GA-K-means 聚類算法。該方法彌補了K-means 在尋找全局最優解方面的不足，在穩定性和有效性方面都明顯好于傳統K-means 聚類算法。