細長橢球體在水中自由下落的運動特性實驗研究1)
詹 軍 張 杰 陽倦成,2) 倪明玖,?
?(西安交通大學航天航空學院機械結構振動與強度國家重點實驗室,西安 710049)
?(中國科學院大學工程科學學院,北京 100049)
引言
多顆粒流動廣泛存在于自然現象和工業領域中,比如植物種子的傳播、大氣污染物的擴散、流化床中顆粒的運動等.多顆粒流動的行為取決于許多因素,比如擾動、粒子之間的相互作用以及作用于不同尺度的自身動力[1].這使得大量的多顆粒多尺度模型非常復雜并且依賴于對相關現象認知的進步.在一些情況下單個顆粒的動力學行為對多顆粒流動行為有很重要的影響,因此單個顆粒運動特性的研究對于進一步研究多顆粒運動行為有著重要的意義.單個顆粒由于受到浮力和重力的作用,往往呈現出不穩定的運動形態(比如擺動、翻滾、混沌、盤旋的運動狀態),這些現象背后潛在的物理機理引起了眾多學者的關注,Ern 等[2]綜述了球體、圓盤、圓柱等顆粒運動特性的實驗和數值結果,然而,目前對于橢球體(包括長扁橢球體和橢球型圓盤) 的研究甚少,對其的研究將進一步促進對顆粒在液體中運動的特性的理解,具有十分重要的研究價值.
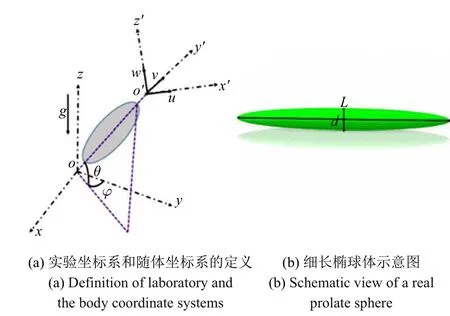
在球體尾跡和路徑方面,文獻[3-6]對均勻流中球體的各種尾跡結構進行了詳細的數值研究,但并未揭示流動不穩定發生的潛在機理.隨后Provansal等[7-8]用實驗驗證了前人的數值結果:當Red< 212,球體的尾跡是軸對稱結構,當212 相比球體顆粒,非球型顆粒由于其幾何特征的各向異性,其運動過程將產生不一樣的運動特征,相應的尾跡和路徑不穩定性會變得更加復雜[13-14].Marshall 等[15]圓盤運動的實驗表明當Red超過臨界值時,固定的圓盤尾跡中會有周期性發卡渦脫落;這在文獻[16-18]的數值結果里得到驗證,且球體不同的運動狀態和尾跡結構也得到確認.Field 等[19]對自由下落圓盤進行實驗研究后表明存在定常運動、周期運動、翻滾、混沌等4 種運動類型,隨后Auguste[20]也在數值模擬中觀察到了同樣的結果.Willmarth 等[21]對于圓盤的實驗表明,當Red< 100時圓盤的運動是穩定的,隨著雷諾數增大,開始出現周期性運動.Zhong 等[22]對圓盤的研究發現在40 圓柱顆粒的運動過程有別于圓盤的運動過程.Namkoong 等[25]對自由上升或下降的無限長圓柱進行了二維數值模擬,在0.5<<4,65 然而當顆粒為細長橢球體時,其形狀介于球體與圓柱之間,在流體中的運動形態將有明顯的區別,目前的研究還主要集中在數值模擬方面.Xia 等[29]研究了單個二維橢球體在牛頓流體中的下沉過程,結果表明流體區域的寬度對橢球型顆粒的運動形態有著顯著的影響.Mehdi 等[30]對單個細長橢球體進行了三維數值模擬,結果表明細長橢球體運動過程中會繞其長軸旋轉.Li 等[31]在研究橢球型顆粒在剪切流中的特性時也同樣發現了這一旋轉現象.Fornari等[32]采用浸沒邊界法研究了多個橢球體的運動過程,發現顆粒的平均下降速度隨著顆粒的體積分數的增大而減小,且均小于單個顆粒運動時的最終速度.然而,采用理論和數值模擬方法雖能非常深入地了解橢球體的運動特性,但其中一些結果還有待實驗的進一步驗證.本文主要通過實驗對不同縱橫比的細長橢球體的運動特性開展研究.首先介紹了實驗平臺、實驗材料和數據處理方法;然后分別討論了物體運動的路徑、速度、振蕩頻率、尾渦結構;最后總結了細長橢球體運動特點. 為了開展細長橢球體在水中自由下落的運動特性研究,我們搭建了包含兩臺高速攝像機的顆粒追蹤系統,實驗系統如圖1 所示,由主體框架、水箱、高速攝像機、光源、釋放裝置等幾大部分組成.主體框架由鋁合金制成,作為整個實驗系統的載體;水箱為高1200 mm,橫截面為300 mm×300 mm 的有機玻璃制成,作為顆粒在水箱中運動的實驗段,前人的大量實驗已證明直徑小于10 mm 的小球在這種水箱中運動時,壁面的影響可以忽略不計;兩臺高速攝像機(Phantom MIRO LC 311,實驗所用分辨率1280×800,拍攝幀頻為25),用于記錄顆粒的整個運動過程;兩臺LED 燈與兩臺高速攝像機分別相互垂直放置在升降臺上(升降平臺運動速度可調,并始終保持顆粒在運動過程中始終處于相機視野內)如圖1(b)所示,并且將有燈光一側的水箱壁面貼上柔光紙(為了使燈光均勻的照射拍攝區域);頂端的電動釋放裝置用于顆粒的釋放,并且與之相連的伸縮桿可以調整釋放裝置與液面的距離;調平地腳用于調整系統水平,底座用于放置水箱,移動滾輪用于移動系統的位置. 圖1 實驗系統圖Fig.1 Sketch of the experimental system 圖2 實驗顆粒形狀以及相應的坐標系Fig.2 Particle shape in experiments and the corresponding coordinate system 實驗中所使用的細長橢球體是用樹脂材料3D打印的,樹脂密度ρc=1.2±0.05 g/cm3.3D 打印可以很好的控制橢球體的尺寸,其真實物理形狀如圖2(b) 所示,其中L表示細長橢球體的長軸,d表示短軸,在實驗前會將打印的橢球體進行打磨以確保物體表面光滑,然后測得的長短軸長度的打印誤差在5%以下,可以滿足實驗的要求,每種工況打印兩個橢球體.橢球體的幾何信息可以用兩個參數來描述,即縱橫比L/d,以及等效直徑D=在本實驗中,所選橢球體幾何參數范圍為:L/d=2 ~10,等效直徑為D=5 ~10 mm,(L/d,D) 組合參數有30組.本實驗在有機玻璃制成的水箱中進行,水箱中加入過濾后的自來水,并保證液位高度在1150 mm,實驗在室溫(20±5?C) 環境下進行,對應水的密度為ρf=0.996±0.004 g/cm3,運動黏性ν=1.02×10?6m2/s. 實驗前將水箱中裝滿水并靜置幾個小時,并將實驗顆粒用電動夾爪夾緊,且同時保證細長橢球體的長軸為水平狀態并位于液面以下,以保證顆粒無初速度入水.每次實驗過程中,通過設定升降平臺的運動速度以保證顆粒始終在相機的視野中,后期在數據處理過程中,將相機拍攝得到的顆粒運動速度與平臺運動速度進行疊加,進而得到顆粒的真實運動速度.每組工況用兩個不同的橢球體進行兩次重復實驗,且保證兩次實驗的間隔時間為1 h 左右,以減小流體內部運動對固體顆粒運動特性的影響.需要注意的是,根據Toupoint 等[28]的研究表明,對于圓柱體而言,其初始的運動角度帶來的影響對圓柱體下落的最終運動形態沒有影響,因此,本文暫時不考慮細長橢球體在不同初始角度下落的情形. 實驗中不考慮橢球顆粒和液體密度的影響,因此顆粒的下沉狀態完全由(Ar,L/d)來決定,其中Ar是阿基米德數,表示顆粒所受重力和黏性力的比值,其定義方式為 其中ρc和ρf分別表示橢球體和液體的密度,ν 表示液體的運動黏性系數.值得注意的是,顆粒下沉的終態雷諾數Red對研究其運動狀態也很有意義,因此我們對不同工況下的Red也進行了統計,如表1 所示.為了研究方便,在本文中若無特殊說明,長度用D進行無量綱化,時間用D/u0進行無量綱化,其中u0=[(ρc/ρf?1)gd]1/2. 表1 不同工況下物體運動屬性Table 1 Characteristic properties of the 30 flow conditions considered in this study 通過背光拍攝的方法,采用兩臺相互垂直的高速攝像機獲取物體兩個方向上的投影圖像,相機輸出的結果分別是(x,z) 和(y,z) 平面灰度圖像,其中z為垂直方向,(x,y)為水平面,如圖2(a)所示.標定得到的圖像空間分辨率為每個像素0.2 mm,圖像處理得到的物體尺寸與實際尺寸誤差在10%以下.然后用兩臺高速攝像機跟蹤拍攝得到物體在(x,z) 和(y,z) 兩個平面的投影圖像序列,最后通過我們編寫的MATLAB 圖像處理程序,將灰度圖像轉化為二值化圖像從而獲取物體的邊界,得到物體5 個自由度的信息.圖3 為橢球體L/d=10,Ar=1389.70 參數下(x,y,z,θ,φ)5 個自由度隨時間的演化情況,圖3(a)為實驗室坐標系下該橢球體的三維路徑圖,圖3(b) 為同一個橢球體偏轉角θ (橢球體長軸與水平面的夾角,如圖2(a) 所示) 和方位角φ (橢球體長軸在(x,y) 平面的投影與y軸的夾角)隨時間的變化,圖3(c)和圖3(d)為重心的三維坐標(x,y,z)隨時間的演化. 由于實驗中所用的實驗室坐標系對應得到的物體運動是三維的,為了將顆粒的運動簡化成本文所關心的兩個方向的運動,這里我們通過兩個方向角度θ和φ 將實驗室坐標系變換為隨體坐標系(Lamb[33]和Toupoint 等[28]),(o′為隨體坐標系原點,o′y′平行于橢球體的長軸),如圖2(a)所示,然后就可以從實驗室坐標系下的速度(ux,uy,uz) 推導出在隨體坐標系下的速度(u,v,w),如式(2)所示 圖3 典型細長橢球體的運動特征Fig.3 Time histories of the falling behaviors of a prolate sphere 對于非平面運動就可以采用以上的坐標系變換來描述物體運動,如圖4 所示,從圖4(a)和4(b)對比可以看出,通過將實驗坐標系變換到隨體坐標系,Z字形振蕩就更加明顯. 圖4 兩個不同坐標系下各速度分量的對比(a)實驗室坐標系下(b)隨體坐標系(圖2(a)中所定義的),Ar=1389.70,L/d=10Fig.4 Comparison of the velocity components(a)in the laboratory frame;and(b)in the system of rotating with the body(defined in Fig.2(a)). Ar=1389.70,L/d=10 在所研究的(Ar,L/d) 參數空間內,我們進行了30 種工況的實驗(包括60 次實驗).在Ar=400~1400,L/d=2~10 參數范圍內主要觀察到了5種路徑類型和Ern 等[2]定義的幾種典型的運動特征保持一致,分別是A 狀態:小振幅不規則運動、B 狀態:小振幅高頻振蕩運動、C 狀態:大振幅低頻振蕩運動、D 狀態:高度非線性運動和直線狀態(包括垂直和傾斜直線). 圖5 展示了不同路徑在參數空間(Ar,L/d) 的分布情況.直線運動主要發生在L/d=4,10;Ar=400~1000,其中L/d=10 下路徑為豎直的直線,L/d=4 下路徑為傾斜的直線.Z 字形振蕩運動(包括B 和C狀態) 主要發生在(Ar,L/d)≈(400~1400,6~10) 范圍內,主要特點是作三維周期性震蕩運動.除此之外,還有兩種不規則運動狀態,包括小振幅不規則運動(A狀態)和高度非線性運動(D 狀態).其中A 狀態發生在(Ar,L/d)≈(400~1400,2~6),而D 狀態發生在(Ar,L/d)≈(400~1400,2),兩個都是混沌運動.需要指出的是,圖5 中出現的數據點重疊現象是由于同樣工況下小球運動產生的兩種不同的狀態. 圖5 不同路徑在(Ar,L/d)平面的相圖Fig.5 Map of the different paths observed in the plane(Ar,L/d) 圖6 給出了不同運動狀態下偏轉角和水平速度的演化過程.從圖中觀察可以發現A 狀態的偏轉角θ 在0?~10?之間不規則振蕩,低于Z 字形振蕩運動(這與Toupoint[28]的不規則II 很類似),水平速度也都是小振幅不規則震蕩;B 狀態的偏轉角θ 在0?~30?為振幅逐漸增加的諧波振蕩,ux對應的振幅先增加而后趨于穩定值,uy對應的振幅較小,且不規則; C狀態的偏轉角θ 是恒定振幅為20?的諧波震蕩,ux是振幅為恒定值諧波振蕩以及uy為振幅增加的諧波振蕩,圖3 和圖4 分別描述了(Ar,L/d)≈(1389.70,10)的細長橢球顆粒在水中作Z 字型振蕩運動時其路徑和速度隨時間的變化規律,從圖3(a) 和3(b) 可以發現顆粒在水平方向的位移振幅在1.5D~3D之間,偏轉角θ 的震蕩頻率為1.5 Hz 左右,為狀態B 的1.5 倍.進一步從圖4(a) 也可發現豎直速度分量uz是水平速度(ux,uy)振蕩頻率的兩倍,這些現象與Fernandes等[34]和Toupoint 等[28]得到的結果一致,這種現象是由顆粒在做Z 字形運動時顆粒兩側周期性渦脫落引起的,渦每脫落一次就會產生阻力的變化,從而引起豎直速度的振蕩,而水平速度的振蕩則與升力相關,需要渦脫落兩次才完成升力的一個周期性變化.高度非線性運動的偏轉角θ 在0?~15?之間不規則振蕩,ux為小振幅不規則振蕩以及uy是大振幅不規則振蕩;直線運動的偏轉角θ 為恒定振幅3?的諧波振蕩,其水平速度都是小振幅不規則震蕩.這樣通過不同路徑的偏轉角和水平速度隨時間演化的特點可以對路徑進行清晰地分類. 圖6 不同路徑類型所對應的典型物體的偏轉角θ 以及水平速度隨時間的演化比較,A 狀態:小振幅不規則運動(L/d=2,Red=449.02)、B 狀態:小振幅振蕩運動(L/d=6,Red=372.08)、C 狀態:大振幅振蕩運動(L/d=10,Red=474.60)、D 狀態:高度非線性運動(L/d=2,Red=1304.29)、直線運動(L/d=10,Red=149.76)Fig.6 Comparison of the time of inclination angle θ and horizontal velocity of the typical prolate sphere corresponding to different path types,for the low-amplitude irregular motion(L/d=2,Red=449.02),for the low-amplitude fluttering(L/d=6,Red=372.08),for the high-amplitude fluttering(L/d=10,Red=474.60),for the highly nonlinear motion(L/d=2,Red=1304.29),and for the rectilinear motion(L/d=10,Red=149.76) 為了進一步研究其運動特性,本節對物體的速度以及阻力進行定量的分析和討論.將物體從靜止釋放后,我們將兩次實驗的垂直下降的最終速度進行平均得到,速度的范圍為65.8~167.62 mm/s.對于給定的(Ar,L/d),兩次實驗的平均速度相對誤差在8%以內,通過兩次數據平均的方法以降低實驗誤差. 圖7 給出了隨著Ar和L/d的變化,平均下落最終速度的變化情況,可以從圖中明顯看出,隨著Ar的增加(顆粒體積增大),顆粒的下落最終速度呈現線性的增加;而當固定小球體積時(Ar固定)隨著細長橢球體的長短軸比L/d的增加,其下落最終速度逐漸減小.這一現象產生的主要原因是L/d的增加所帶來的細長橢球體迎風面積增大,進而導致其運動阻力增大、最終下落速度減小.進一步地,我們基于平均速度、橢球體的短軸長d定義了雷諾數Red=/ν,并建立阻力與浮力的平衡關系如下面公式,其中Cd表示阻力系數,可以得 圖7 不同L/d 下終態速度與Ar 之間的關系Fig.7 Average terminal velocity versus Archimedes number for various L/d 其中γ=4π(d/2)2L/6 為細長橢球體的體積,S=πdL/4 為橢球體在下落時的迎風面積. 進一步,通過采用u0對顆粒下降的最終速度進行無量綱化,結果如圖8 所示.從圖中可以看出,無量綱化的顆粒最終速度與Ar的變化基本無關,這一結果與Toupoint[28]得到的結論一致.但本文中的無量綱最終速度隨著細長橢球體的長短軸比的增加有少許減小的趨勢,表明較長的橢球體具有較小的相對速度,這一現象產生的原因還有待進一步的研究. 圖8 在不同L/d 下無量綱化平均速度與Ar 之間的關系Fig.8 Average vertical velocity scaled by the gravitational velocity versus the Archimedes number for various elongation ratios 圖9 給出了各種實驗工況下的阻力系數與Red的關系,并將本實驗結果與前人文獻中圓柱自由下落的結果進行對比.在實驗參數范圍內,阻力系數Cd=0.7~1.5.本文結果與Jayaweera 等[35](L/d>100的金屬圓柱在不同密度的液體中下落) 和Toupoint等[28](2L/d20 的塑料圓柱在水中下落)的實驗結果進行比較,可以發現本文結果與Jayaweera 等[35]的結果符合較好,而與Toupoint 等[28]的實驗結果有一定的偏差.產生這一現象的主要原因是實驗過程中本文的細長橢球體的偏轉角為θ=0?~30?,比Toupoint 等[28]的圓柱下落時的偏轉角(θ < 25?) 要大一些,較大的偏轉角引起顆粒運動過程中產生更大的阻力.從圖9 中還可以看出,顆粒下落的阻力系數在Red< 200 時,隨著Red增大呈現急劇下降的趨勢,而當Red200 時,顆粒下落的阻力系數變化趨于平緩. 圖9 自由下落的橢球體阻力系數Cd 與Red 之間的關系Fig.9 Drag coefficient of the freely falling prolate spheres versus Reynolds number 通過將細長橢球體的偏轉角θ 進行頻譜分析,我們獲得了其球體下落過程的擺動頻率,并繪制在圖10(a) 中.從圖中可以看出,頻率f=ω/2π 的范圍為0.7~2.2 Hz,且隨著Ar數的增大而逐漸減小.對比L/d=2 的短橢球體,其擺動頻率隨Ar數的增大而迅速減小,從2.2 Hz 下降到1.4 Hz 左右;而對于較長的橢球體,L/d=10,其擺動頻率隨Ar數增大減小較小,從1.0 Hz 左右下降到0.7 Hz 左右.若將無量綱長度變為L0=,特征速度不變,將振蕩頻率f進行無量綱化得到S t?=f L0/u0.從圖10 可以看出S t?幾乎與L/d和Ar無關而趨于恒定的值0.12.這與Fernandes 等[36]短圓柱的實驗(L/d=0.1 ~0.5)結果和Toupoint 等[28]細長圓柱的實驗(L/d=2 ~20)結果S t?=0.11 相比非常接近.由于這些物體的振蕩頻率隱藏在固有的和附加的慣性項以及考慮黏性和尾跡效應的渦流貢獻之間的復雜平衡中,因此沿著這個思路進一步研究存在于物體表面的不穩定邊界層特征. 圖10 不同L/d 下偏轉角,振蕩頻率f 及無量綱化后的S t?隨Ar 的演化對比Fig.10 Comparison of the oscillations frequency f and the S t?of the body inclination angle versus the Ar for various elongation ratio L/d 由于物體振蕩的頻率f大于黏性擴散頻率v/d2(6 倍L/d=10,Ar=491.33 到175 倍L/d=10,Ar=1389.70),因此遠離物體表面的渦黏性擴散就會受到限制以至于速度劇烈變化以適應無滑移邊界條件.下面引入非定常邊界層厚度δ=作為相關的特征長度尺度[25].圖11(a) 表明與橢球體的短軸d的尺度是相當的,在相同L/d下,隨著Ar的增大而減小;在相同體積下,隨著L/d的增大而增大.鑒于這一變化關系我們將δ 用L0無量綱化后發現δ與L/d無關,隨著Ar的增大而線性減小,如圖11(b)所示.因此L/d的作用可以通過特征長度L0和δ 來獲得,圖10 和圖11 的結果可以用圖12(a)和圖12(b)兩種形式來闡釋.圖12(a) 說明基于δ 無量綱化的=fδ/u0是與L/d無關的,并且和Ar的關系可以用=1.25Ar?0.5進行擬合,隨著Ar的增大而減小.圖12(b)是基于δ 的Reδ=u0δ/v也與L/d無關而隨著Ar的增大而線性增大,這與圖7 形成對比.圖12(a)和圖12(b) 中和Reδ對于Ar的依賴性和對L/d的獨立性說明物體的體積的重要性而不再是具體的形狀,以及橢球體的尖端在控制運動物體非定常邊界層擴展具有重要的作用. 圖11 在不同的L/d下,不穩定邊界層厚度δ分別在橢球體短軸長d和L0=的無量綱化下隨著Ar的演化Fig.11 Thickness of the unsteady boundary layer δ versus Ar for various elongation ratios,normalizedwiththe prolate sphere minor axisd and L0= 圖12 基于不穩定邊界層厚度δ 的S t?= fδ/u0,Red=u0δ/ν 與Ar 的關系Fig.12 Based on the thickness of the unsteady boundary.S t?and Reynolds number versus Ar 圖12 基于不穩定邊界層厚度δ 的S t?= fδ/u0,Red=u0δ/ν 與Ar 的關系(續)Fig.12 Based on the thickness of the unsteady boundary.S t?and Reynolds number versus Ar(continued) 最后對細長橢球體在水中自由下落過程中不同路徑所對應的尾渦結構和特性進行定性的分析,實驗前先將橢球體放入高濃度的熒光素鈉溶液中浸泡兩個小時,然后取出風干使其均勻的覆蓋在橢球體表面,主要為了使染色的球體運動足夠遠的距離以便能更好的觀察渦演化的過程. 分別對小振幅不規則運動(A 狀態)、Z 字形振蕩運動(包括B 和C 狀態,由于Z 字形運動的尾渦是類似的,因此選取了一組大振幅振蕩的尾渦)、高度非線性運動(D 狀態)、直線運動各選取一組典型橢球體進行尾渦可視化實驗.如圖13 所示,左圖為該橢球體重心的三維位置及其偏轉角θ 演化的示意圖,右圖為相應的尾渦隨時間的演化圖.圖13(a)對應于A 狀態,其特征是會觀察到不相連的發卡狀渦交替從細長橢球體兩側交替脫落,其脫落的頻率為6~7 Hz,這與Veldhuis 等[37](對于Red=608,=1.05)的球體尾跡類似.圖13(b)對應于C 狀態,由于尾跡與物體運動的耦合以及物體軸相對于速度方向的角度影響從而導致了明顯不同的尾跡,其特征是細長橢球體的兩側脫落渦時會產生一個周期性變化的升力從而導致物體周期性振蕩運動; 渦脫落的頻率和豎直速度振蕩的頻率是相同的,偏轉角θ 振蕩頻率是其一半,這是因為物體兩側各脫落一次渦時分別對應于偏轉角θ 一個周期的波峰和波谷; 渦剛開始從平衡位置脫落和脫落完成時對應的豎直速度達到最大值,相應的加速度達到最小,這與Toupoint 等[28]在Red=585,L/d=5 的圓柱觀察到的尾跡是類似的;圖13(c)對應于運動類型D,其特征是在高雷諾數下尾跡呈現出混沌的狀態,這與Veldhuis 等[37](對于Red=1261,=2.63) 的球體的尾跡類似,同樣類似的尾渦結構在Cano-Lozano 等[38]文中的氣泡作混沌上升時也被觀察到,在他們的數值模擬中,發現氣泡在高雷諾數情況下做無規則的混沌運動,但路徑振幅顯著小于氣泡作Z 字型或者螺旋型運動時,大概只有氣泡直徑的1/10 或者更小,這些特征與圖13(c)的結果相符.圖13(d) 對應于直線運動類型,其特征是在細長橢球體兩側會周期性地脫落出旋轉方向相反、左右交替脫落的漩渦,這種漩渦具有一定的脫落頻率,這也被稱為卡門渦街; 這與Toupoint 等[28](對于Red=50,L/d=10 的塑料圓柱)以及Jayaweera[35](對于Red=70,L/d=10 金屬圓柱)實驗中的尾跡幾乎是一樣的,其脫落的頻率也在6~7 Hz. 通過對不同細長橢球體尾跡的觀察可以發現,一方面隨著雷諾數的增加,尾跡會變得越來越不規則;另一方面當L/d→1 時,細長橢球體的運動狀態和球體的類似,L/d→10 時,細長橢球體的運動狀態和細長圓柱(L/d=10) 的類似.由于實驗參數范圍有限,因此沒有觀察到文獻[28] 中提到的條紋狀渦(L/d=3,Red=120) 以及傾斜的渦脫落模式(L/d=20,Red=130),后面會擴大參數范圍進一步理解和分析細長橢球體在液體中的運動特性. 本文通過實驗研究了細長橢球體在液體中自由下落的運動特性,通過高速攝像機拍攝其運動過程和尾渦結構,然后獲取其運動路徑、方向角度、振蕩頻率等的變化趨勢,并通過進一步分析得到以下結論: (2) 在相同參數范圍下本文研究的細長橢球體受到的阻力系數Cd明顯大于Toupoint 等[28]對于圓柱阻力系數的測量結果,產生阻力增大的主要原因是本文研究的橢球體相比圓柱體在下落時的偏轉角更大. 圖13 不同路徑以及對應的尾跡隨時間的演化,每幅尾跡圖的上下圖分別為該時刻的正視圖和側視圖(a)小振幅不規則振蕩運動(L/d=2,Red=449.02)(b)大振幅低頻振蕩運動(L/d=10,Red=474.60)(c)高度非線性運動(L/d=2,Red=1304.29)(d)直線運動(L/d=10,Red=149.76)Fig.13 Examples of the time of evolution of three-dimensional path and corresponding wake,the upper and lower parts of each wake diagram are the front view and the side view of the time,respectively,(a)for the low-amplitude irregular motion(L/d=2,Red=449.02);(b)for the high-amplitude fluttering(L/d=10,Red=474.60),(c)for the highly nonlinear motion(L/d=2,Red=1304.29);and(d)for the rectilinear motion(L/d=10,Red=149.76) (4)通過對各種路徑下尾渦的研究,首先驗證了Mehdi 等[30]中細長橢球體會繞垂直軸旋轉這一結論.其次通過對不同細長橢球體尾跡的觀察可以發現,一方面隨著雷諾數的增大,尾跡會變得越來越不規則;另一方面當L/d→1 時,細長橢球體的運動狀態和球體的類似,L/d→10 時,細長橢球體的運動狀態和細長圓柱(L/d=10)的類似.1 實驗系統及數據處理方法
1.1 實驗系統介紹



1.2 圖像處理方法
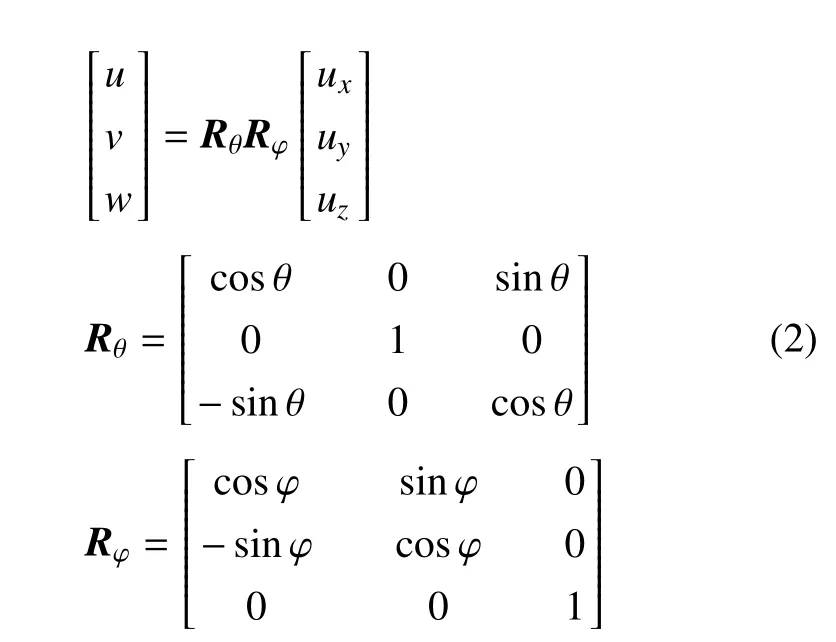


2 實驗結果與分析
2.1 細長橢球體的運動軌跡分析


2.2 速度和阻力分析




2.3 振蕩頻率的分析




2.4 物體尾渦可視化研究
3 結論


