無模逆運算的橢圓曲線數字簽名算法

肖 帥，王緒安，潘 峰

1.武警工程大學 網絡與信息安全武警部隊重點實驗室，西安710086

2.武警工程大學 密碼工程學院，西安710086

1 引言

數字簽名算法（DSA）是1991 年8 月由美國國家研究所（NIST）提出的標準和技術[1-3]，它的安全性是基于離散對數（DL）在Zp*的素數階子群中的計算不可追溯性的問題（DLP）。作為信息與數據安全的核心技術之一，它可以實現身份認證、數據完整性保護、防篡改、防冒充和不可否認性等數據傳輸中的重要需求[4]。Johson等人[2]在2001年提出了橢圓曲線數字簽名（Elliptic Curve Digital Signature，ECDSA）算法，它是通過2 次模逆運算、3次標量乘運算來實現數字簽名的過程的。橢圓曲線數字簽名是重要的信息保護技術之一，它通過為信息增加簽名，有效保護了信息的完整性、不可否認性、認證性、不可偽造性，目前這一算法得到了廣泛認可和應用[5]。圖1顯示的是ECDSA的發展歷程。

圖1 ECDSA發展歷程

橢圓曲線數字簽名算法（ECDSA）是對數字簽名算法（DSA）的模擬。橢圓曲線密碼（ECC）由Koblitz N[6]和Miller V[7]于1985 年發明，是目前安全性最高的公鑰加密算法，它是基于橢圓曲線的一種公鑰體制。相較其他公鑰體制，橢圓曲線密碼的單位比特強度要高一些。橢圓曲線密碼體制的主要優勢是計算參數更小，密鑰更短[8]，運算速度更快，簽名也更加短小[9]，效率也更高[10]。因此橢圓曲線密碼性能優良，應用廣泛，尤其適用于存儲空間、處理能力、帶寬及功耗受限的場合[11]。

表1 顯示的是基于公鑰密碼的數字簽名體制的分類：在這三種分類中，ECDLP 是最難解的，除幾類特殊橢圓曲線外，至今仍沒有ECDLP的有效求解算法。

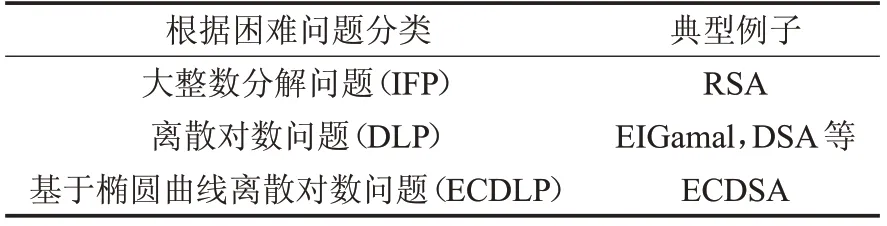
表1 基于公鑰密碼的數字簽名體制分類

數字簽名應用廣泛，電子商務和網絡安全認證的核心技術就是數字簽名，最近大火的區塊鏈技術，其底層技術之一就是數字簽名。由于數字簽名方案是許多保密協議的核心構造塊，因此提高數字簽名方案的效率是非常重要的[12]。

在對ECDSA 的深入研究過程中，一般一致認為影響ECDSA 簽名耗時主要有兩個計算因素[13]：一是標量乘法運算[14]，標量乘法運算是已知橢圓曲線上兩個點：基點G 和隨機數k，求kG 的運算過程。另外一個也是最主要的運算就是模逆運算，由于在乘法運算中至少要進行1次求逆運算，而模逆運算所需要消耗的時間是乘法運算的10倍[2]，所以耗時主要由求逆運算產生。針對ECDSA 計算的耗時問題，對求逆運算和標量乘運算的各種改進的方案[15-21]相繼被提出，詳見表2。

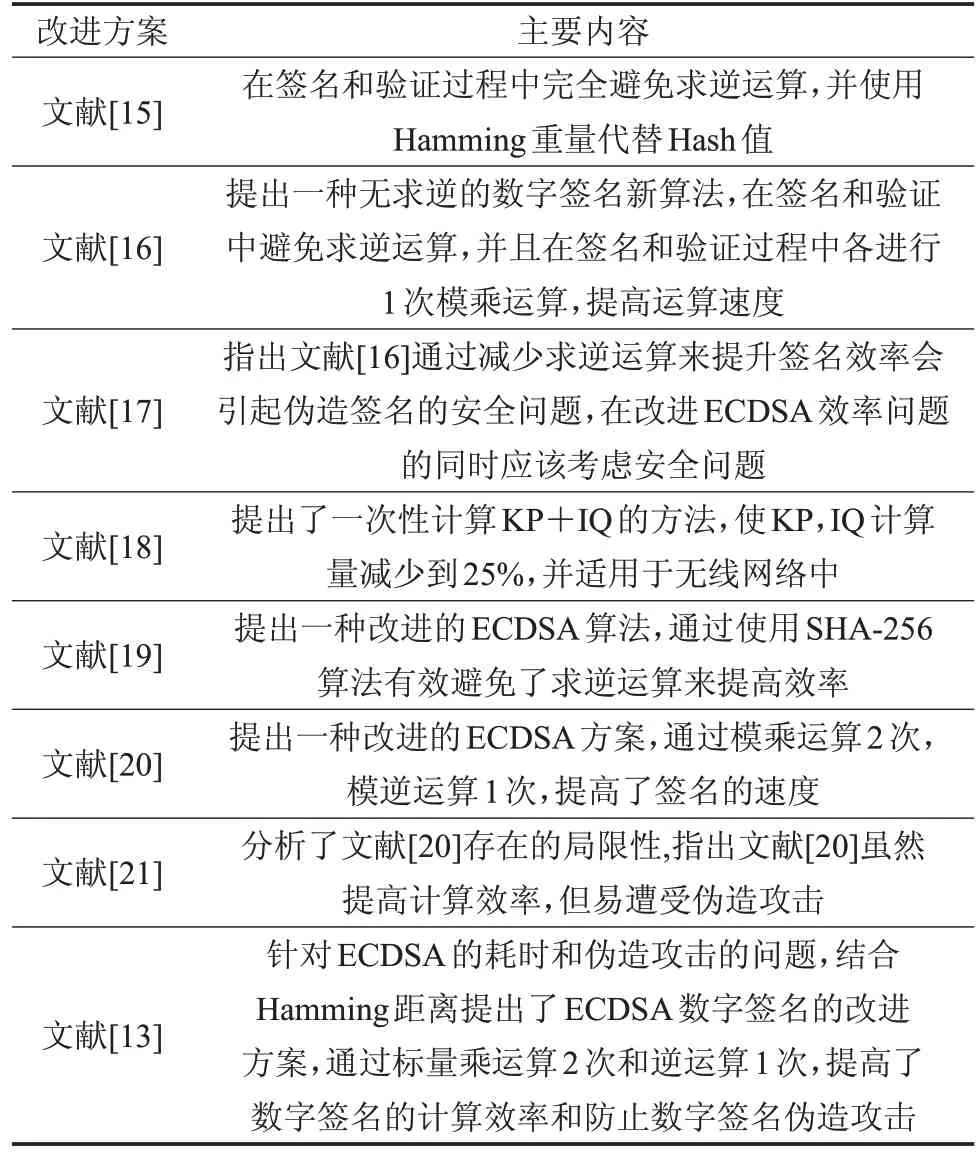
表2 對求逆運算和標量乘運算的各種改進的方案

本文在分析研究經典的橢圓曲線密碼理論的基礎上，針對經典ECDSA 方案中存在的耗時和偽造攻擊的問題，通過引入雙參數和避免求逆運算，提出了一種改進的能實現高效率的數字簽名方案。

2 預備知識

2.1 方案參數與釋義說明

本文方案描述所涉及的參數符號及釋義如表3所示。

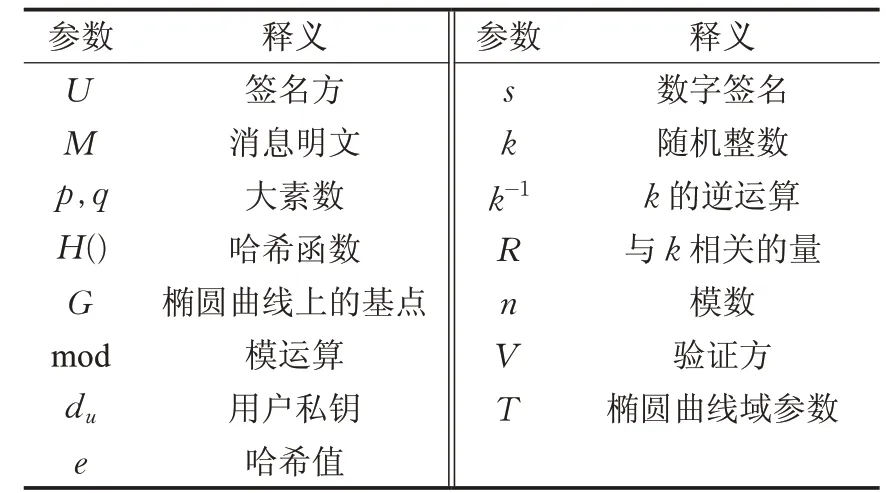
表3 參數符號與釋義

2.2 橢圓曲線密碼體制

橢圓曲線密碼體制可以看作是舊的離散對數（DL）的橢圓曲線類似物，ZP*的子群被有限域上橢圓曲線上的點群所代替。以下是ECC的一般結構：

設P ∈(FP)，點Q 是P 的倍數，即存在正整數X ，使得q Xp，然后用給定的p 和q 定義ECDLP。基于橢圓曲線離散對數問題，產生了橢圓曲線密碼體制。

設E 為橢圓曲線，p 為E 上的一個點，如果存在正整數N ，使得NP=0，則n 是點P 的階數，其中O 是無窮大點。

橢圓曲線公鑰密碼（ECC）體制的構造如下：

選擇域Fp，橢圓曲線E，選擇點P(xp,yp)，n 為E上的素數階。公開信息：有限域Fp，曲線方程E，點P及其階n，計算Q=dP，取Q 點為公鑰，整數D 為密鑰。

要向Alice發送秘密信息M ，需要執行以下步驟：

（1）在域Fp 中將明文M 表示為元素M ；

（2）隨機選取[1,n-1]中的整數k；

（3）計算點(x1,y1)=kP；

（4）計算點(x2,y2)=kQ，如果x2=0，則重新選擇k；

（5）計算c=mx2；

（6）發送(x1,y1,c)給Alice。

當Alice接收到密文時，使用密鑰D 計算密文。

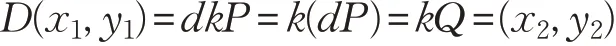
這里Q=dP 是公開的。如果破譯者能夠解決橢圓曲線上的離散對數問題，就可以從dP 中還原出d ，完成解密[22]。

2.3 橢圓曲線離散對數問題（ECDLP）

橢圓曲線離散對數問題是對于橢圓曲線E( GF( q))上任意兩點G 和Q，有Q=dG，在已知G 和Q 的前提下求出小于q 的正整數d。己知d 和G 計算Q 比較容易，但是已知Q 和G 計算d 則很困難，這便是橢圓曲線加密體制的核心。橢圓曲線密碼體制的安全性基于橢圓曲線離散對數問題，也就是求解ECDLP 算法的時間復雜度。

3 ECDSA數字簽名原理與方案分析

3.1 ECDSA數字簽名方案描述

ECDSA 是ECC 與DSA 的結合，整個簽名過程與DSA類似，所不一樣的是簽名中采取的算法為ECC，最后簽名出來的值也是分為r,s。

（1）方案建立

U 為簽名者，V 為驗證者：

①U 構建橢圓曲線城參數T=(p,a,b,G,n,h)；

②U 建立密鑰對(du,Qu)，且有Qu=duG；

③U 選擇一個hash數；

④U 將hash函數和橢圓曲線域參數T 傳給V 。

（2）簽名算法

①選擇一個臨時密鑰對(k,r)，其中R=kG=(xR,yR)和域參數T 相關。

②令r=xRmod n，如果r=0，返回1。

③計算待簽消息的hash值H=H(m)，將H 轉換成整數e。

④計算s=k-1(e+rdu)(mod n )，如果s=0，返回1。

⑤輸出S=(r,s)為數字簽名。

（3）驗證算法

V 通過驗證從U 發來的數字簽名來判斷所接收消息以及對方身份的真偽。

①如果r,s ?[1 ,n-1] ，驗證不通過。

②計算待簽消息的hash值H=Hash(M) ，將H 轉換成整數e。

③計算u1=es-1( mod n ),u2=rs-1(mod n )。

④計算R=(xR,yR)=u1G+u2Qu，如果R=0，驗證失敗。

⑤令v=xR(mod n )，如果v=r ，驗證成功，否則驗證失敗。

3.2 ECDSA數字簽名方案分析

在ECDSA 方案中，公鑰的產生算法是Qu=duG ，在簽名的生成和驗證過程中需要分別計算k-1mod n 和s-1mod n，即需要進行模逆運算。若模乘運算的數據規模為n ，則一次模乘運算的復雜度為O(n2ln n)。表4分析了ECDSA方案的算法復雜度。

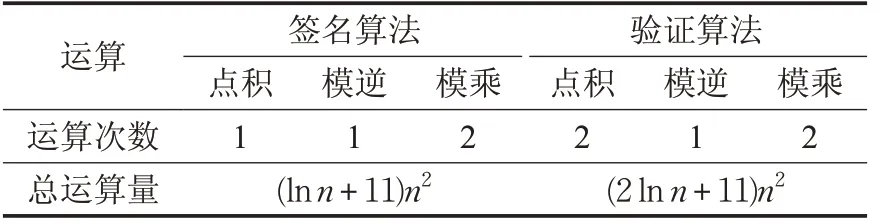
表4 ECDSA算法復雜度分析

可以看到，簽名算法和驗證算法運算很復雜，都有模逆運算。前文中已經提到，在現有的橢圓曲線加密或者簽名過程中，主要的運算負擔來自求逆運算，求逆是最復雜費時的操作，一次求逆的時間大約相當于80 次點乘運算。如果可以減少甚至是避免模逆運算無疑有助于數字簽名效率的提升。

4 改進的ECDSA方案

由以上分析可知，在簽名或者驗證階段，如果可以減少甚至是避免模逆運算無疑有助于數字簽名效率的提升。但在著力提高運算效率的同時也應兼顧安全問題，基于此，本文提出了一種新的ECDSA的改進方案。

4.1 改進方案的算法描述

設ECC 參數為T={a,b,G,n,h}，用戶使用私鑰A( d,Q )對消息m 進行簽名，圖2顯示了簽名和驗證的具體過程。

（1）A隨機選擇一個整數k，k ∈[1,n-1]；

（2）計算kG=(x1,y1) ，將x 轉換成整數xˉ；

（3）隨機選擇1組α,β ∈[1,n-1] ，α,β 滿足條件k=αr+βm；

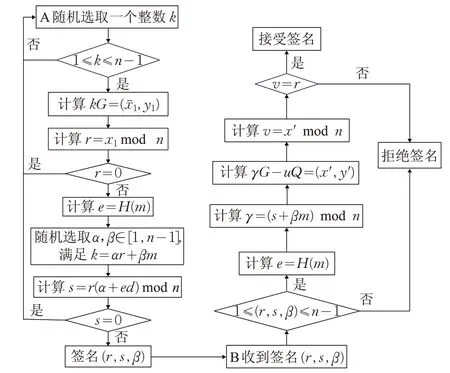
圖2 改進的算法流程圖

（4）計算待簽名的消息m 的哈希值e，e=H(m)；

（5）計算r=xˉ1mod n；其中若r=0，則跳轉到（1）；（6）計算s=r(α+ed)mod n；若s=0，則跳轉到（1）；（7）(r,s,β)即為簽名m 的信息.用戶B收到m 和(r,s,β)后，對簽名進行如下驗證：

①驗證r,s,β 是否屬于區間[1,n-1]內的整數，若三者中任何一個參數驗證失敗，則拒絕簽名；

②計算e=H(m)；

③計算γ=(s+βm)mod n，u=er mod n；

④計算γG-uQ=(x′,y′)；

⑤計算v=x′mod n；

⑥若v=r，則驗證簽名成功。

在以上改進方案的算法描述細節部分，步驟（1）至步驟（3）中關于隨機數k 的選取，進行分析說明，以表明方案中隨機數選取的合理性和隨機性。

通過（1），確定了一個整數k，k 是在[1,n-1]區間隨機選取的，在（3）中，等式的兩邊都要進行模n 運算，由于n 為素數，r,m 為已知信息，k 被隨機選取后，再從[1,n-1]區間任意選取一個α，則一定存在一個滿足等式k=αr+βm 的整數β，且β ∈[1,n-1]，所以改進方案的構造具有合理性和隨機性。

對改進算法的正確性證明如下，若(r,s,β)是對m的簽名信息，則：

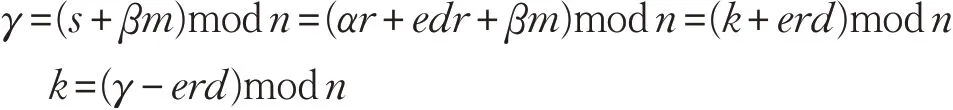
因此

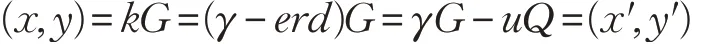
所以有ν=x′=x=r mod n

4.2 改進方案的算法分析

（1）抗替換信息的偽造攻擊

A發送(r,s,β)信息給接收方C后，接收方C可以用偽造消息m′來代替m 進行簽名。

C偽造簽名過程如下：

①由于s,e，r 為已知量，C 由s=r(α+ed)mod n 可計算出(α+ed)mod n；

②使用替換的消息m′，計算e'=H(m') ；

③計算滿足條件k=αr+βm 的α,β；

④計算s′=r(α+e′d)mod n；

⑤偽造簽名計算s′=r(α+e′d)mod n，(r,s′,β )為m′的簽名數據。

B收到(r,s',β )簽名信息后，進行如下簽名驗證，計算：

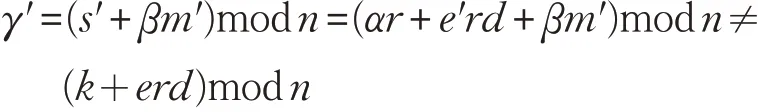
因此簽名無效。

（2）替換隨機數的偽造攻擊

接收方C收到簽名消息(r,s,β)后，可以偽造隨機數k′來代替k 進行簽名。C偽造簽名過程如下：

①由于s,e,r 已知，B 由s=r(α+ed)mod n 計算出(α+ed)mod n；

②隨機生成一個整數t，計算k'=k+t，其中k',k 都是未知的；

③計算k'G=(k+t)G=kG+tG=(x′,y′)；

④計算r'=x'mod n；

⑤計算滿足條件k′=α′r′+β′m 的α′,β′；

⑥計算e=H( )m ；

⑦計算s′=r′(α′+ed)mod n。

B 收到( r′,s',β′ )簽名信息后，進行如下簽名過程：計算γ′=(s′+β′m)mod n=(α′r′+er′d+β′m)mod n ≠(x1,y1)，因此簽名無效，通過以上分析可知，改進的ECDSA算法可以有效抵御接收者偽造簽名。

4.3 改進方案的性能分析

4.3.1 安全性分析

方案的構造通常不難，但首要的是要考慮到它的安全性，否則即使數字簽名計算效率再高，也毫無意義。在本文的改進方案中，即使非法用戶設法得到了A或B的私鑰，也很難獲取到會話密鑰。由QA=dAG 可知，如果攻擊者在竊取QA和G 后推出了dA，那么就意味著他解決了離散對數難題，而這是不可能的，因此攻擊者無法獲得私鑰。具體安全性有以下幾個方面。

（1）抗偽造攻擊

對于發送方A和接收方B，雖然e,r′,α′，(α+ed)mod n是公開已知的，但是接收方B驗證出來的x′與x 不同，所以可以有效地抵抗偽造攻擊。

（2）防數據篡改

通過對消息進行哈希運算可以實現數據的完整性，一旦數據遭到篡改，哈希數值將會發生變化，從前述步驟中可以看出，如果哈希值不相同，則簽名無法通過。

（3）抗中間人攻擊

在傳統的通信過程中，公鑰是公開的，私鑰可以是隨機數r 或分發給用戶的d 。攻擊者選取隨機數rc∈[1,n-1]，截獲A發給B的QA=dAG ，B發給A的QB=dBG ，將dAG,dBG 修改成rcG ，協商之后，A與非法用戶共享密鑰dAdBG，A誤認為B是共享的，B與非法用戶共享dAdBG，而B認為A是共享的，實際A和B沒有共享密鑰。當A發送信息給B時用dArcG 對信息進行加密，非法用戶截獲之后進行解密，偽造信息，用dAdBG 加密后發送給B，這樣就欺騙了用戶A和B，而事實上A和B是不知情的，這樣正常的密鑰協商就受到了影響。因此，在不清楚對方真實身份的情況下，通信雙方建立的密鑰會話易遭受中間人攻擊。在本文方案中通信的雙方實現了身份的雙向認證，非法用戶不能偽裝成任何一方，從而有效地防止了中間人攻擊。

（4）抗抵賴性

接收方根據發送方發送的(r,s,β)，防止發送方事后抵賴。

4.3.2 效率分析

在本文的方案中，簽名和驗證過程均沒有模逆運算，通過具體的數值來分析改進方案的效率變化。在數字簽名過程中耗時主要集中在乘法、逆運算和標量乘運算，可分別簡記為[l],[i],[h ] ，鑒于加法等運算對耗時的影響因素較小，故可忽略不計。1次求逆運算約相當于10次乘法運算，即[i] =10[l ]，根據文獻[18]，標量乘運算是滿足在163b 下[h ] =75[i] + 173[l ]=750[l ]+173[l ]=923[l]，設模乘運算的數據規模為m，表5是改進后的新方案與經典的ECDSA 方案的耗時對比，由表5 分析可知，本文改進的方案在簽名上的計算效率比經典的ECDSA 方案提高了0.96%，在驗證上的計算效率比ECDSA方案提高了50.2%。

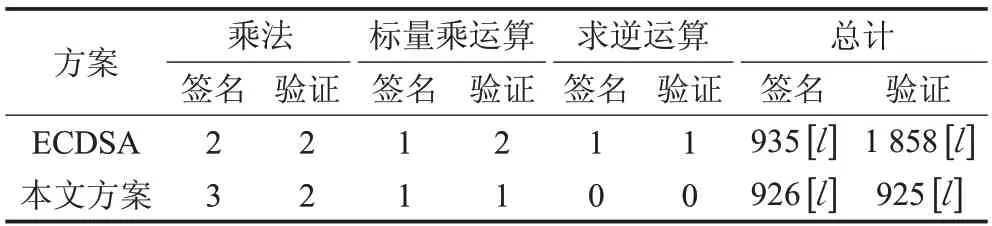
表5 兩種方案耗時對比

4.3.3 仿真實驗

在本文的改進方案中，簽名和驗證過程均沒有求逆運算，理論上無疑會極大提升數字簽名的效率，使用MATLAB編程模擬仿真來進行驗證，檢測效率如圖3所示，從圖中可以直觀地看到兩種方案的運算復雜度與數據規模的關系。

由圖3可看到，相較經典的ECDSA方案，在同等的數據規模下，本文的改進方案中數據復雜度始終較低，實驗仿真結果與本文的理論分析相吻合，即本文的改進方案可以提高數字簽名的計算效率。

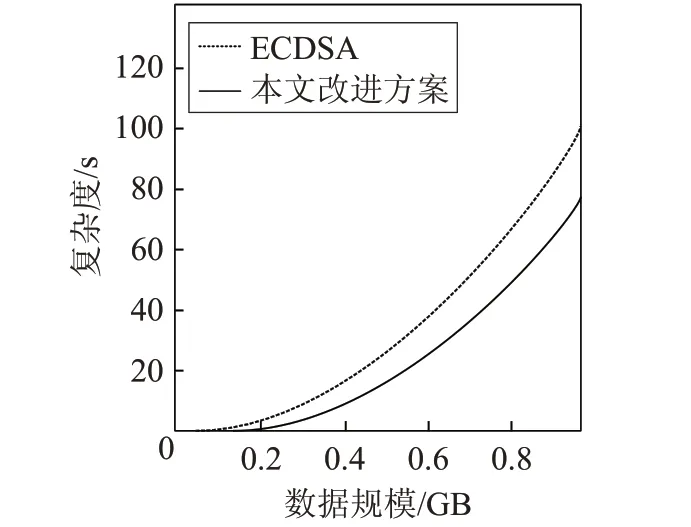
圖3 復雜度與數據規模對比

5 改進的ECDSA方案在電子商務中的應用

信息化網絡時代，電子商務的飛速發展使得人們足不出戶就可以享受方便快捷的服務。電子商務對信息的保密性、數據完整性、不可否認性有較高要求。人們在享受網上交易帶來的便捷服務的同時，也日益關注信息安全。RSA 簽名算法曾被廣泛使用來保護交易信息的安全，隨著MD5算法被破解，SHA-1算法受到挑戰和ECDSA在理論上的日益成熟，ECDSA算法的優越性日益凸顯，電子商務的安全越來越需要ECDSA來保證。

將改進的ECDSA方案與時下飛速發展的電子商務進行結合，在交易信息的加解密模型中通過構建Meneses-Vanstone 密碼體制來對數據進行加解密操作。基于改進的橢圓曲線Meneses-Vanstone（MV）密碼體制構造數據加解密模型。

數據加密模型如圖4所示。

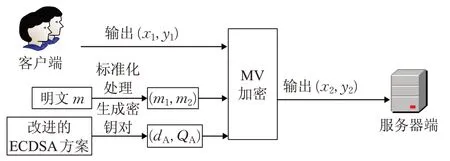
圖4 電子數據加密模型

在電子商務交易過程中主要是客戶端與服務器端的互動，客戶端即加密的一方，為電子商務中數據信息的發送方。

（1）客戶端將待發送傳輸的數據信息格式化處理生成消息串(m1,m2)。

（2）用數據信息的接收方服務器端的公鑰QB和客戶端的私鑰dA按照MV 密碼體制對(m1,m2)進行加密形成密文(x2,y2)。

（3）客戶端將自己的公鑰QA和加密信息( QA,( x2,y2))一起發送給接收方服務器端。

MV加密過程如下：

（1）獲得服務器端的公鑰QB，計算( x1,y1)=dAQB，如果x1,y1=0，則客戶端重新選擇私鑰dA，同時生成新的公鑰。

（2）計算x2=m1x1mod p,y2=m2y1mod p。

MV解密過程如下：

（1）獲得客戶端的公鑰QA，計算( x1,y1)=dBQA。

（2）計算m1=mod p,m2=mod p。

數據解密模型如圖5所示。

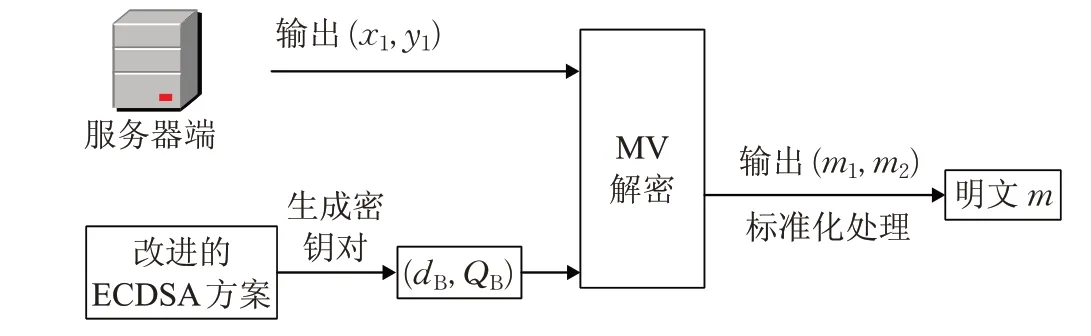
圖5 電子數據解密模型

服務器端即解密方，為電子商務交易中數據信息的接收方。服務器端接收到客戶端發送過來的加密信息( x2,y2)，首先使用客戶端的公鑰QA和服務器端的私鑰dB對加密信息按照MV密碼體制進行解密生成( )m1,m2，然后再將其逆向轉換為客戶端明文消息。

MV 加密體制并沒有限制消息明文必須嵌入橢圓曲線上，這種體制的優點是不需要將待加密的數據進行數據類型轉換操作，從而降低了成本，同時提高了數據加解密效率。無模逆的橢圓曲線數字簽名算法，使運算負擔減少，從而加快數字簽名和驗證簽名的速度，進而使電子商務交易過程安全高效。

6 結束語

本文在對經典的橢圓曲線數字簽名進行分析的基礎上，指出其存在的局限性，由此進行了方案的改進。改進的方案引入了雙參數，進行標量乘運算2 次，在簽名和驗證過程中均沒有使用模逆運算，理論分析證明了本文方案的安全性，仿真實驗證明了改進方案提高了數字簽名的計算效率。最后將改進的方案應用到電子商務中，構建了電子商務交易過程中電子數據的加解密模型。