多邊形激勵下動車組動態響應研究

張國平，張志波，吳興文，蔡吳斌*,

多邊形激勵下動車組動態響應研究

張國平1，張志波1，吳興文2，蔡吳斌*,2

（1.中車青島四方機車車輛股份有限公司，山東 青島 266111；2.西南交通大學 牽引動力國家重點實驗室，四川 成都 610031）

首先基于剛柔耦合理論，考慮了輪對、軸箱和構架的柔性，建立了動車組車輛剛柔耦合動力學模型；然后又通過模態疊加法建立了軌道的動力學模型，從而發展成車線－剛柔耦合動力學模型。隨后，在車輪上施加20階理想多邊形，研究了300 km/h下軸箱垂向加速度、輪軌垂向力和輪軸彎曲應力的響應，結果表明：軸箱垂向加速度和輪軌垂向力以577 Hz的多邊形通過頻率波動，而輪軸彎曲應力主頻為28.8 Hz的車輪轉頻，在此基礎上，疊加了多邊形的通過頻率，因此多邊形的通過頻率577 Hz會分岔為548 Hz和605 Hz兩個頻率。通過對不同速度和不同多邊形幅值下車輛響應的研究可以得到以下結論：隨著速度和多邊形幅值的增大，輪軌力最大值總體上呈現增大趨勢。從輪軌力最小值上看：速度越大，多邊形幅值越大，則更容易發生輪軌分離。當車輪多邊形通過頻率與輪軌耦合共振頻率耦合，會引起輪軌垂向力的增大。當與軸箱自身模態頻率耦合時會導致軸箱加速度的變大。輪軸應力則主要受到輪軌耦合共振模態以及輪軸自身的彎曲模態影響。

剛柔耦合動力學；車線耦合動力學；車輪多邊形；輪軌垂向力；輪軸彎曲應力

近年來，我國高速鐵路快速發展，但也遇到了一些輪軌磨耗問題。其中，車輪非圓化現象[1-2]，即車輪多邊形問題出現在部分高速動車組中。車輪多邊形會引起輪軌高頻異常振動，惡化簧下部件振動水平，進而可能會影響列車的運行安全。

關于車輪多邊形的成因尚無定論。在瑞典，測試表明新車輪存在三階多邊形，經過分析[3]，是在車輪的制造過程中，三角爪的車輪固定方式所導致。我國的地鐵車輛中發現了9階車輪不圓，李偉[4]對車輛進行了線路振動測量以及輪對模態測試，試驗結果表明9階車輪多邊形是由輪對的一階彎曲模態引起的。Morys[5]認為輪對的動不平衡會加速車輪的非圓化磨耗發展。通過建立動力學模型和輪軌磨耗模型，Johansson[6]再現了車輪多邊形的發展，認為軌道的反共振以及輪軌耦合共振均有可能導致車輪多邊形的產生。近年來我國高速鐵路出現了高階車輪多邊形現象，對于250 km/h速度級的列車，車輪多邊形以22～24階為主；而對于300 km/h速度級的列車，多邊形通常為17～20階。Wu[7]通過試驗研究表明，我國高速鐵路的多邊形符合“頻率固定”機理，車輪多邊形的階數依賴于動車組的速度。Wu[8]和Cai[9]通過仿真再現了我國高速列車的高階多邊形生長過程，并認為其與鋼軌的局部彎曲模態有關。

車輪多邊形現象會引起輪軌力的異常波動，從而對車輛動力學性能、結構振動及輪軌噪聲等均帶來負面影響。張雪珊[8]通過車輪多邊形對車輛穩定性的研究發現，車輪橢圓化可能導致車輛臨界速度的下降，進而引起乘坐平穩性的惡化。王興宇[11]研究了車內噪聲與車輪多邊形之間的關系，研究表明車內振動噪聲的頻率與車輪多邊形磨耗的通過頻率有對應關系，這意味著車輪多邊形可以顯著影響車內噪聲。劉歡[12]分析了機車車輪多邊形對其振動特性的影響，結果表明，通過車輪鏇修可以顯著降低機車振動水平。吳磊[13]研究了車輪多邊形磨耗下的脫軌系數，雖然不同工況下的脫軌系數仍在安全限制之內，但需要指出的是：除了脫軌系數，車輪多邊形還會引起車輛和軌道振動的加劇，進一步導致結構應力的增大，從而可能引發結構失效縮短結構壽命，帶來安全性問題。Wu[14]針對多邊形下激勵的輪對疲勞損傷極限進行了研究，研究表明為了防止輪軸出現疲勞損傷，應縮短探傷的間隔。

基于此，本文針對車輪多邊形，從振動、輪軌力和輪軸應力三個方面，系統地研究了車輪多邊形對動車組動態響應的影響。通過仿真的手段，首先建立了動力學模型，包括剛柔耦合模型和車線耦合模型。其次，將理想的20階多邊形施加在車輪表面，對車輛的軸箱垂向加速度、輪軌垂向力和輪軸動態應力進行分析，研究其響應規律。最后，在不同的車速和不同的車輪多邊形幅值下，分析了軸箱垂向加速度、輪軌垂向力和輪軸動態應力的變化規律。

1 車線剛柔耦合動力學模型

為研究車輪多邊形下高速動車組動態響應，首先需建立動車組車線剛柔耦合動力學模型。

1.1 剛柔耦合動力學

由于車輪多邊形的激勵頻率通常較高，傳統的多剛體動力學模型覆蓋的頻率有限，難以滿足車輪多邊形的仿真要求，因此本文基于模態綜合法和應力模態恢復法，考慮了構架、輪對和軸箱的柔性振動，建立了剛柔耦合動力學模型，如圖1所示。

剛柔耦合動力學模型采用Simpack建立，并利用了其與有限元軟件ANSYS之間的接口，基于子結構模態縮減技術，將各部件的模態信息導入到Simpack中[14]。其中，輪對考慮了固有頻率1000 Hz以下的模態，圖2是輪對的典型模態振型及其對應的固有頻率。輪軸1階至4階的彎曲模態頻率分別為113 Hz、191 Hz、363 Hz以及659 Hz，而在303 Hz和445 Hz時，輪對的模態振型則分別為輪盤的反相位和同相位傘狀變形。在仿真中，本文不僅計算了輪對的柔性振動響應，同時也采用模態應力恢復技術，實時計算其動態應力。

此外，轉臂式軸箱的固有頻率相對較高，前兩階固有模態頻率分別為535 Hz和579 Hz，從圖3中可以看出，它們分別對應了轉臂的一階彎曲和扭轉振型。

對于構架來說，總體頻率相對較低，對高階多邊形激勵下的響應影響較小。因此構架的模態在這里沒有一一列出。

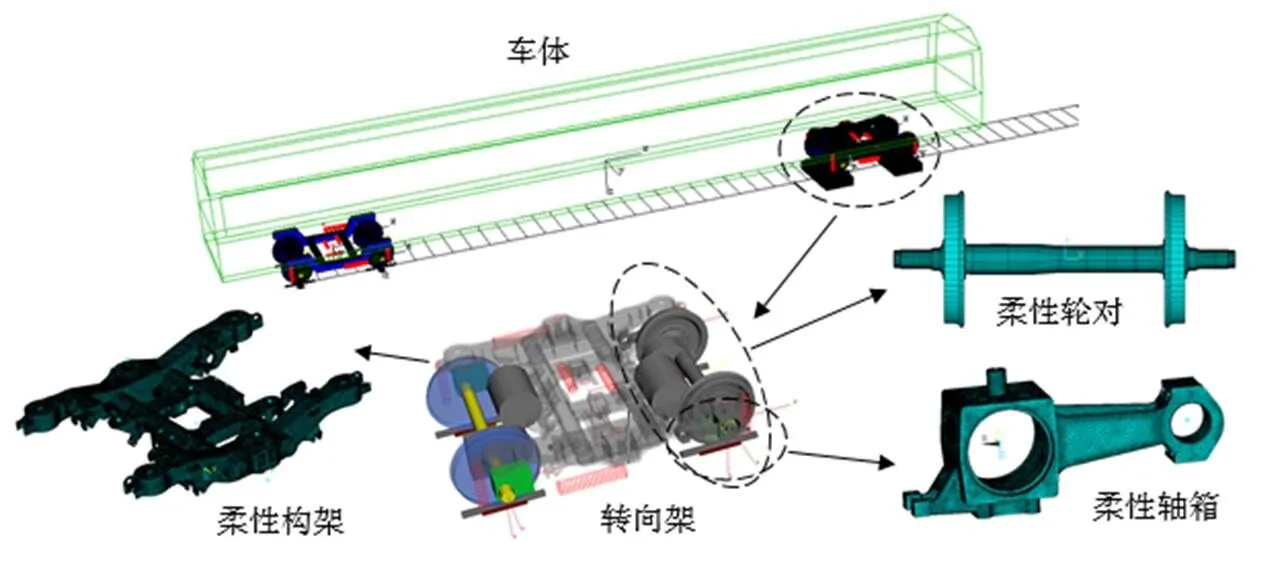
圖1 動車組剛柔耦合動力學模型

圖2 輪對的模態振型

1.2 車線耦合動力學

除了車輛模型外，在輪軌界面高頻的車輪多邊形激振下，軌道的彈性變得不可忽視。因此本文在剛柔耦合模型的基礎上，還基于車輛/軌道耦合動力學理論，建立了車線剛柔耦合動力學模型。在軌道模型中，本文針對CRTSI型板式無砟軌道，將鋼軌考慮為離散支撐的鐵木辛柯梁模型，軌道板則采用有限元的方法建模。它們的響應利用模態疊加法進行計算。扣件和軌道板下的彈性水泥砂漿層則用線性彈簧－阻尼單元來模擬。

基于鐵木辛柯梁理論，鋼軌的彎曲振動可由平動和界面轉動兩個偏微分方程表示，鋼軌垂向振動如式（1）、式（2），橫向振動如式（3）、式（4），扭轉振動如式（5）所示。

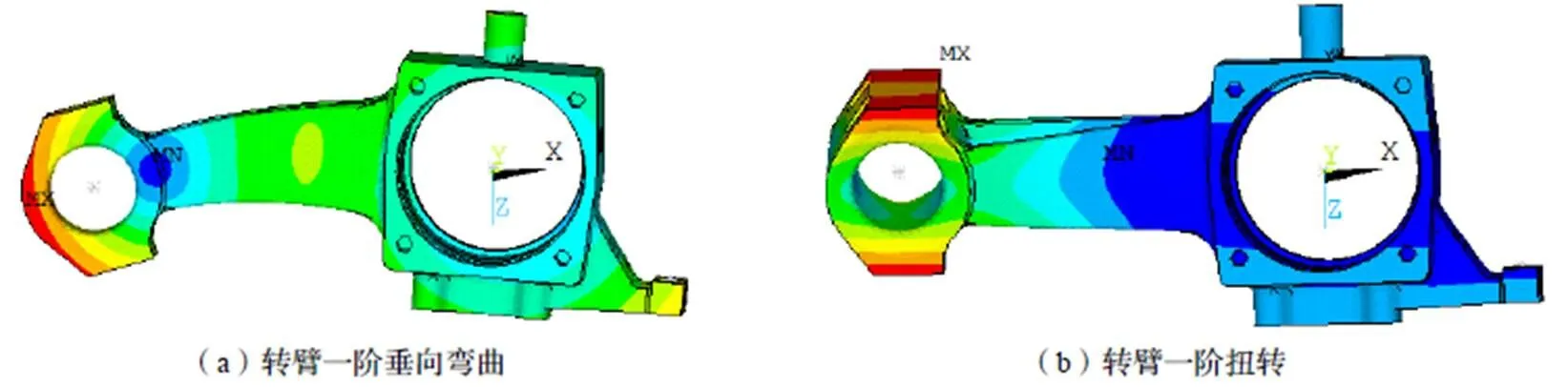
圖3 軸箱的模態振型

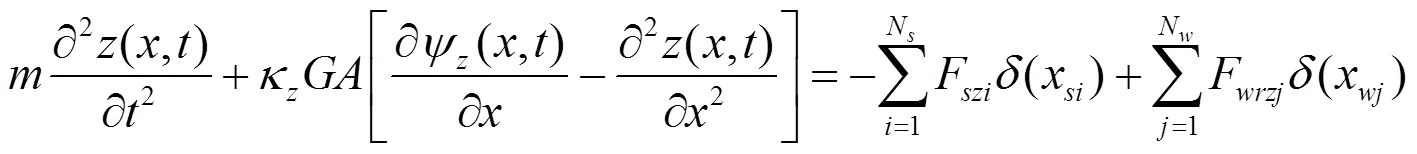
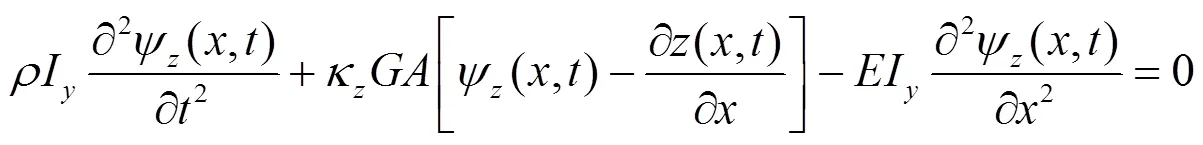
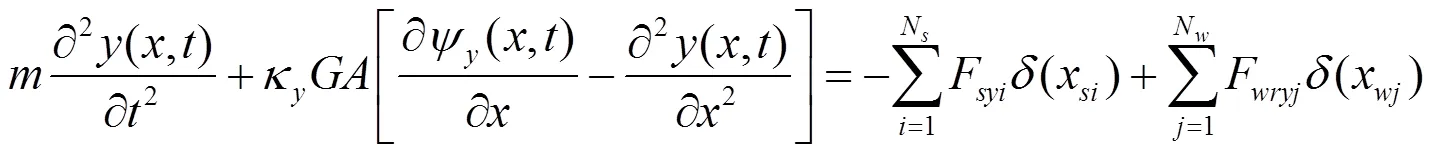
式中：為鋼軌的縱向位置，m；為時間，s；為鋼軌橫向位移，m；為鋼軌垂向位移，m；為鋼軌扭轉角度，rad；ψ為鋼軌繞軸的截面轉角，rad；ψ為鋼軌繞軸的截面轉角，rad；F為軌道第個支點垂向支承反力，N；F為軌道第個支點橫向支承反力，N；F為第位車輪的輪軌垂向載荷，N；F為第位車輪的輪軌橫向載荷，N；M為第支點處軌道支反力矩，N·m；M為第為車輪作用于軌道的力矩，N·m；為鋼軌的彈性模量，Pa；I為鋼軌截面對軸的慣性矩，m4；I為鋼軌截面對軸的慣性矩，m4；0為鋼軌的極慣性矩，m4；為鋼軌單位長度密度，kg/m3；為鋼軌剪切模量，Pa；為鋼軌截面面積，2；κ為鋼軌截面的垂向剪切形狀因子；κ為鋼軌截面的橫向剪切形狀因子；為狄拉克函數。

為了考慮板式無砟軌道的振動，在車輛軌道耦合動力學模型中將軌道板考慮成柔性體，用有限元實體單元建模，并利用模態疊加法進行求解。根據有限元理論其運動方程可描述為：

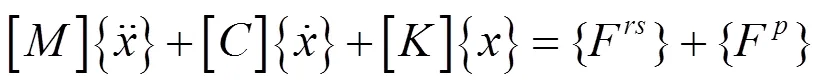
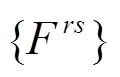
利用模態疊加法和軌道板的正則振型函數，軌道板全局坐標的運動方程可以轉換成一系列解耦的方程，為：

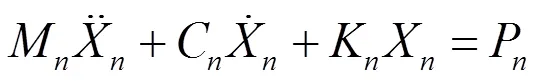
式中：X為軌道板正則坐標；M、C、K為軌道板廣義正則質量矩陣、廣義阻尼矩陣和廣義剛度矩陣；P為廣義正則載荷矩陣；為正則模態階數。

1.3 多邊形激勵模型

本文僅考慮理想的車輪多邊形激勵，如圖4所示。激勵則可以表示為：

式中：R為車輪名義滾動圓處的半徑，m；Ao為多邊形的幅值；N為多邊形階數；為車輪旋轉的角度，rad。

2 典型多邊形激勵下的響應

基于上文中建立的車線剛柔耦合動力學模型，本小節計算了典型的車輪多邊形下動車組的響應，包括軸箱垂向加速度、輪軌垂向力和輪軸彎曲應力。在幅值為0.02 mm的20階理想多邊形激振下，300 km/h運行的動車組的響應（輪徑920 mm）如圖5所示。不難看出，軸箱垂向加速度和輪軌垂向力呈現諧波振動。其中，軸箱垂向加速度的幅值達到40，而輪軌垂向力的最大值接近100 kN，它們的振動頻率為577 Hz，對應的車輪多邊形的通過頻率為：

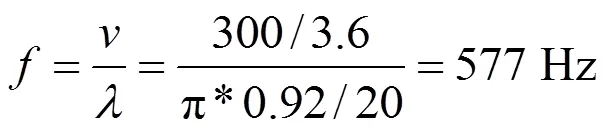
式中：v為車速，m/s；λ為多邊形的波長，m。

輪軸的彎曲動應力響應與它們有所差異。圖6是本文選取的輪軸彎曲應力測點，分別選取了左右輪盤的兩側，以及輪軸中點處的5個測點，在動力學計算時，實時輸出它們的彎曲應力。從圖5可見，輪軸的應力不僅存在577 Hz的高頻振動，同時還呈現出以0.0347 s為周期的低頻波動，通過計算發現，車輪轉動一周需要的時間為：

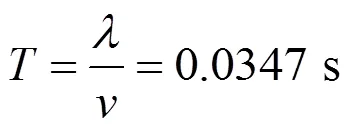
圖7給出了無多邊形工況和20階多邊形工況下的點C處的應力對比，可見，即使在沒有多邊形激勵的情況下，車輛穩態運行時，在車體和構架的靜載荷作用下，再加上輪對的旋轉，輪軸上的節點必然會處于壓縮－拉伸交替循環的狀態，且其頻率應該等于車輪的轉頻。在應力上則體現為在0上下波動，大于0表示拉伸，小于0表示壓縮。當施加了20階多邊形后，在無多邊形的基礎上，又疊加了一個車輪多邊形通過頻率的波動。

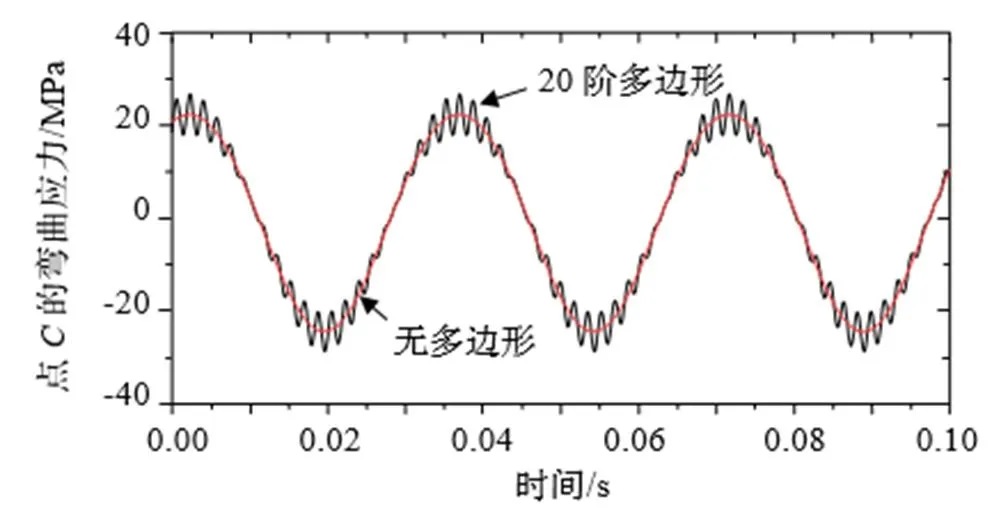
圖7 有無多邊形激勵下輪軸彎曲應力對比

圖8對比了在20階多邊形激勵下，車輛的軸箱垂向加速度、輪軌垂向力以及輪軸彎曲應力的頻域特點：前兩者以577 Hz的多邊形通過頻率為主頻；彎曲應力主頻為28.8 Hz的車輪轉頻，同時由于車輪轉頻的調制作用，車輪多邊形的通過頻率577 Hz會分岔為548 Hz和605 Hz兩個頻率。

3 車速和多邊形幅值的影響

針對20階車輪多邊形，本節分析了不同車速和不同車輪多邊形幅值對車輛響應的影響。圖9為當車輪多邊形幅值為0.02 mm時，車速對輪軌垂向力最大值和最小值的影響，從圖中可見，總體上隨著車速的升高，最大值呈現增長趨勢，最小值呈現減小趨勢。當車速為50km/h時，輪軌垂向力的幅值相對較大，這可能是因為此時車輪多邊形通過頻率（96 Hz）接近輪軌耦合共振頻率。此外，當車速超過225 km/h后，輪軌垂向力最小值為0，這說明出現了輪軌分離現象。當車速超過250 km/h后，輪軌垂向力最大值大于170 kN，超過了我國《高速動車組整車試驗規范》中對輪軌垂向力的限值要求。

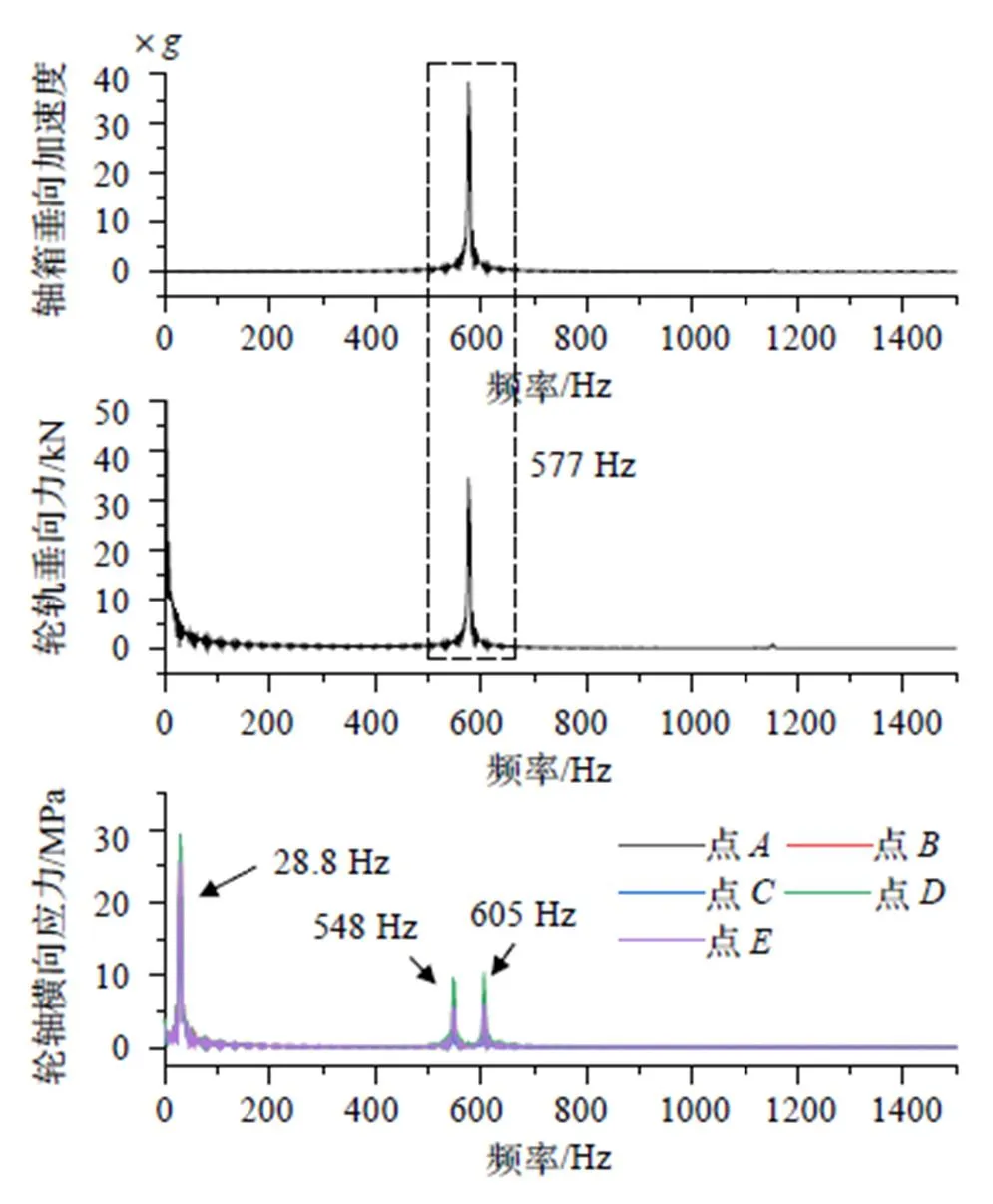
圖8 20階多邊形激勵下車輛響應頻域圖

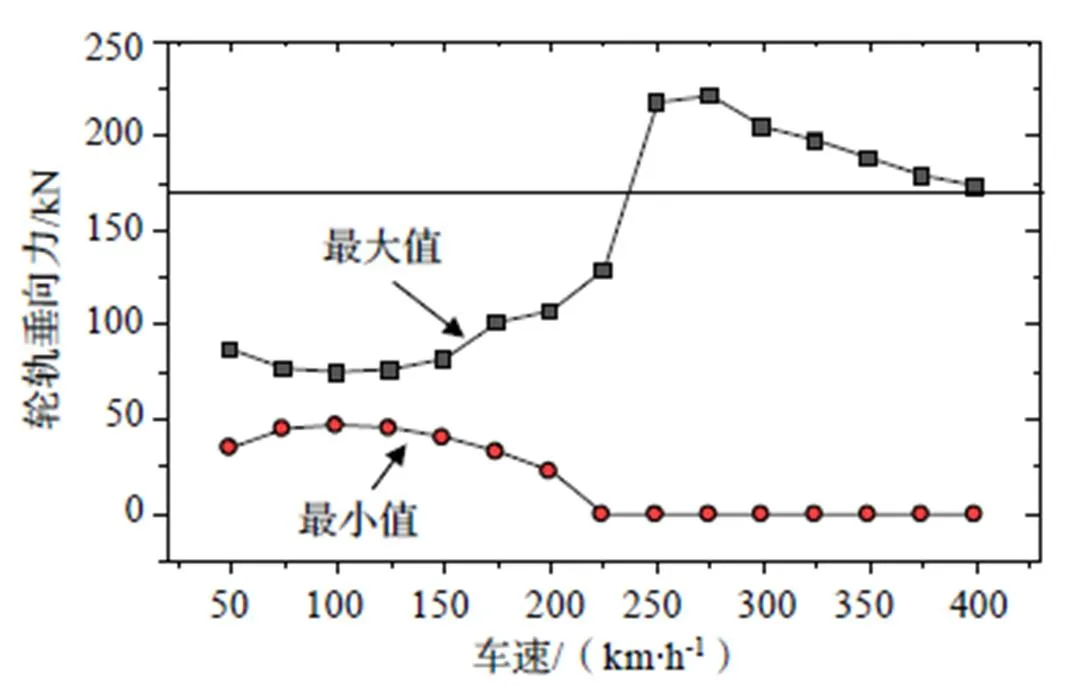
圖9 不同車速下輪軌垂向力最大最小值（20階，0.02 mm）

圖10為200 km/h下，不同車輪多邊形幅值下的輪軌垂向力最大值和最小值。從圖中可見，在發生輪軌分離前（車輪多邊形幅值小于0.14 mm），輪軌垂向力的最大值隨著車輪多邊形幅值的增長基本呈現線性增長的趨勢，而最小值則呈現線性減小的趨勢。當車輪多邊形幅值大于0.14 mm后，出現了輪軌分離現象。

為進一步研究車輪多邊形幅值和車速的影響，圖11分析了當車速從50 km/h增加到400 km/h及車輪多邊形幅值從0.02 mm增加到0.2

mm時，輪軌垂向力的響應。不難看出，其總體趨勢與圖10類似，從最大值上看：隨著速度和車輪多邊形幅值的增大，輪軌垂向力最大值總體上增大。從最小值上看：速度越大，車輪多邊形幅值越大，則更容易發生輪軌分離現象。50 km/h處，輪軌垂向力的最大值出現峰值，最小值出現谷值，可能和輪軌耦合共振頻率有關。

圖10 不同幅值下輪軌垂向力最大最小值（20階，200 km/h）

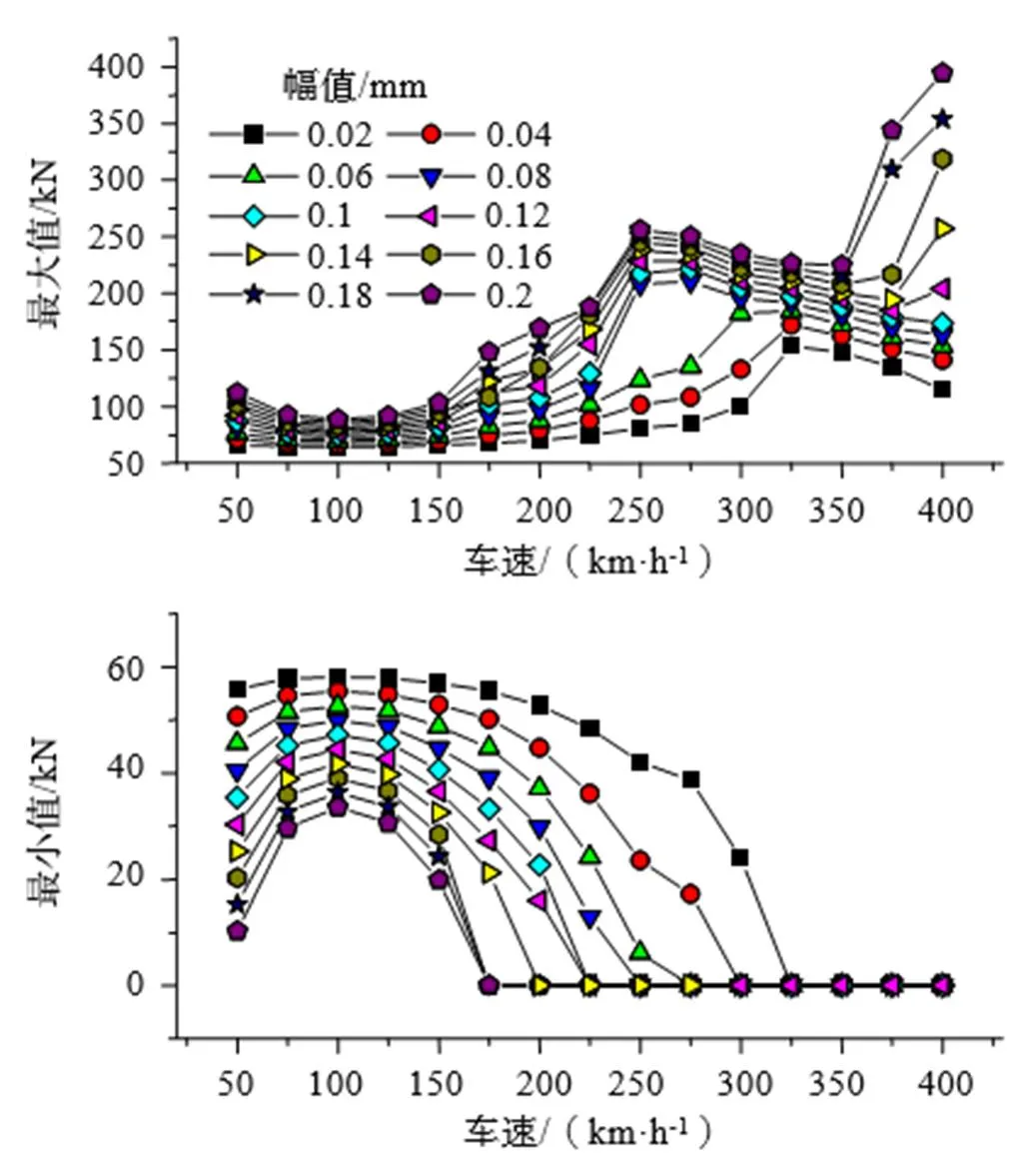
圖11 不同車速和多邊形幅值下輪軌力的最大最小值

圖12為不同車輪多邊形幅值和車速下軸箱垂向加速度的響應。可以看到：首先，隨著車輪多邊形幅值的增加，軸箱垂向加速度逐漸增加。其次，車速在300 km/h時，軸箱垂向加速度出現了峰值。且這個峰值并沒有在輪軌垂向力中體現，所以這可能是由于軸箱自身的模態引起的。從上文可知，軸箱的轉臂彎曲和扭轉固有模態分別為535 Hz和575 Hz；而300 km/h時20階多邊形的通過頻率為577 Hz，與它們接近。從而導致軸箱自身的共振，進一步引起了軸箱垂向加速度的增大。

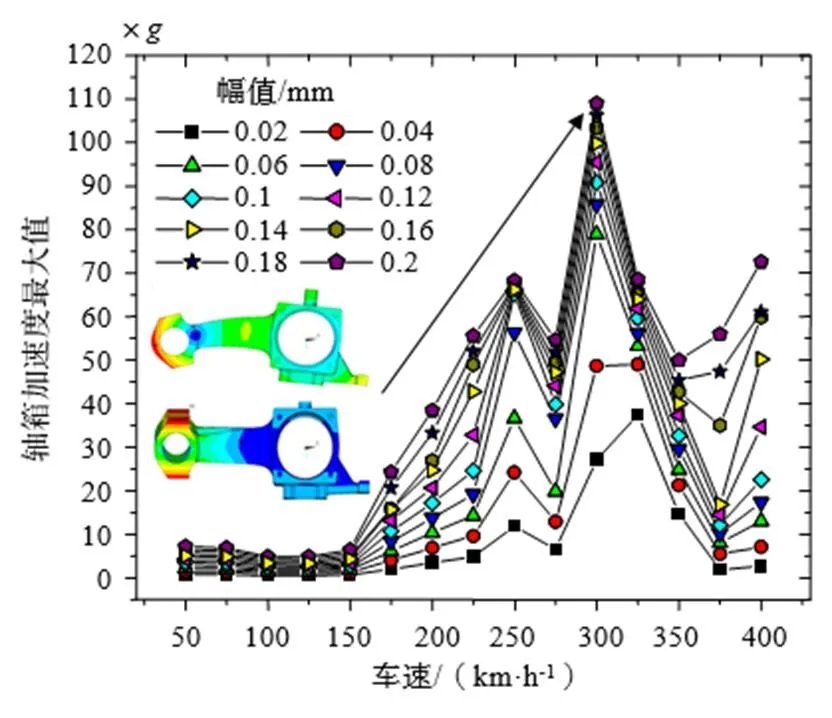
圖12 不同車速和多邊形幅值下的軸箱加速度最大值

圖13為車輪多邊形幅值和車速對輪軸彎曲應力的影響。本文選取了輪軸中心的點進行研究。隨著多邊形幅值的增加，輪軸的彎曲應力是增加的。但車速并不是單調的趨勢，在車速50 km/h和250 km/h時，點處的彎曲應力出現了峰值。前者如前文所述，可能是由輪軌耦合共振所引起。

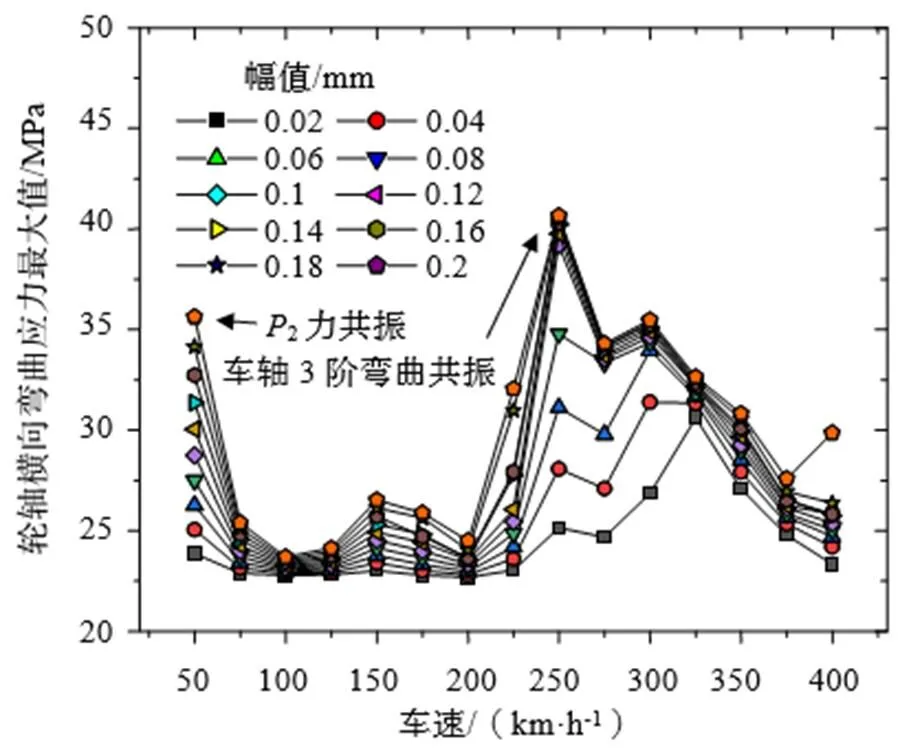
圖13 不同車速和多邊形幅值下的輪軸彎曲應力最大值

對于250 km/h處的峰值，其對應的通過頻率為481 Hz，這可能與車軸的3階彎曲共振有關，從上文可知，雖然車軸的3階彎曲模態在自由狀態下僅有363 Hz，但在一系和輪軌的約束下，在約束狀態下其模態頻率為504 Hz，與車輪多邊形的通過頻率接近，從而引起共振，使得彎曲應力顯著增大。

4 結語

本文考慮了輪對、軸箱和構架的柔性振動，以及軌道的彈性，建立了車線－剛柔耦合動力學模型。對20階多邊形激勵下車輛的響應，包括軸箱垂向加速度、輪軌垂向力和輪軸彎曲應力進行研究，可以得到以下結論：

（1）在20階多邊形激勵下，軸箱垂向加速度和輪軌垂向力的波動以577 Hz的車輪多邊形通過頻率為主頻；而輪軸彎曲應力主頻為28.8 Hz的車輪轉頻，同時由于車輪轉頻的調制作用，車輪多邊形的通過頻率577 Hz會分岔為548 Hz和605 Hz兩個頻率。

（2）隨著速度和車輪多邊形幅值的增大，輪軌垂向力最大值總體呈現增大趨勢。從輪軌垂向力最小值上看：速度越大，車輪多邊形幅值越大，則更容易發生輪軌分離現象。

（3）50 km/h時，輪軌垂向力最大值出現峰值、最小值出現谷值，可能和輪軌耦合共振頻率有關。300 km/h時，軸箱垂向加速度出現峰值，是因為車輪多邊形的通過頻率577 Hz與軸箱的轉臂彎曲和扭轉固有頻率535 Hz和575 Hz相接近，引發軸箱自身共振引起。

（4）輪軸的彎曲應力關于車速不是單調的，輪軌耦合共振以及輪軸的彎曲模態共振均可能導致輪軸彎曲應力的增大。

[1]Nielsen J C O，Johansson A. Out-of-round railway wheels-a literature survey[J]. Proceedings of the Institution of Mechanical Engineers Part F Journal of Rail & Rapid Transit，2000，214（2）：79-91.

[2]Johansson A，Nielsen J O. Out-of-round railway wheels-wheel-rail contact forces and track response derived from field tests and numerical simulations[J]. Proceedings of the Institution of Mechanical Engineers, Part F：Journal of Rail and Rapid Transit，2003，217（2）：135-146.

[3]PALLGEN G. Unrunde rader an eisenbahnfahraeugen[J]. Der Eisenbahningenieur，1998，49（1）：56-60.

[4]李偉，李言義，張雄飛，等. 地鐵車輛車輪多邊形的機理分析[J]. 機械工程學報，2013，49（18）：17-22.

[5]MORYS B，KUNTZE H B.，Hirsch, U.. Investigation of origin and enlargement of out-of-round phenomena in high speed ICE-wheelsets[C]. In Proceedings of 10th European ADAMS Users’ Conference，Frankfurt: s.n.，1995：14.

[6]Johansson A，Andersson C. Out-of-round railway wheels—a study of wheel polygonalization through simulation of three-dimensional wheel–rail interaction and wear[J]. Vehicle System Dynamics，2005，43（8）：539-559.

[7]Yue W U，Xing D U，Zhang H J，et al. Experimental analysis of the mechanism of high-order, polygonal wear of wheels of a high-speed train[J]. 浙江大學學報：A卷英文版，2017（18）：592.

[8]X. Wu，S. Rakheja，W. Cai，M. Chi，A.K.W. Ahmed，S. Qu. A study of formation of high order wheel polygonalization[J]. Wear，2019（424-425）：1-14.

[9]W. Cai，M. Chi，X. Wu，F. Li，Z. Wen，S. Liang，X. Jin. Experimental and numerical analysis of the polygonal wear of high-speed trains[J]. Wear，2019：203079.

[10]張雪珊，肖新標，金學松. 高速車輪橢圓化問題及其對車輛橫向穩定性的影響[J]. 機械工程學報，2008，44（3）：50-56.

[11]王興宇，范軍. 高速列車車內噪聲與車輪不圓順關系的研究[J]. 鐵道學報，2013（9）：18-22.

[12]劉歡，陶功權，羅贇，等. 機車異常振動原因分析和控制措施研究[J]. 機械，2019（8）：1-7.

[13]吳磊，鐘碩喬，金學松，等. 車輪多邊形化對車輛運行安全性能的影響[J]. 交通運輸工程學報，2011（3）：51-58.

[14]X. Wu，M. Chi，H. Gao. Damage tolerances of a railway axle in the presence of wheel polygonalizations[J]. Engineering Failure Analysis，2016（66）：44-59.

[15]包學海. 高速客車車體和構架結構振動研究[D]. 成都：西南交通大學，2009.

Dynamic Response of EMUs in the Presence of Wheel Polygonal Excitations

ZHANG Guoping1，ZHANG Zhibo1，WU Xingwen2，CAI Wubin2

( 1.CRRC Qingdao Sifang Co., Ltd., Qingdao 266111, China; 2.State Key Laboratory of Traction Power, Soutwest Jiaotong University, Chengdu 610031, China )

Based on rigid-flexible coupling theory, rigid-flexible dynamic model of high speed vehicle is established, taking flexibility of wheelset, axle box and bogie frame into consideration. Using the modal superposition method, dynamic model of track is also established. The traditional vehicle dynamic model is improved to vehicle-track and rigid-flexible coupling model. Through applying the 20thorder ideal polygon on the wheel, the response of the axle box vertical acceleration, wheel/rail vertical force and bending stress of the wheelset axle are investigated at the speed of 300 km/h. The results suggest that the axle box vertical accelerations and wheel/rail vertical forces fluctuate at the frequency of 577 Hz, namely, the passing frequency of the polygon. While the dominating frequency of the wheelset axle bending stress is 28.8Hz, which accords with the rotation frequency of the wheel, the passing frequency of the polygon is separated into two peaks at 548 Hz and 605 Hz. Moreover, the effect of vehicle speed and amplitude of the polygon on the dynamic response of the vehicle are studied. The results show that the overall trend of the maximum value of wheel/rail vertical forces increases with the rising of speed and polygon amplitude. As for the minimum value of the forces, the higher speed and larger amplitude would easily lead to the wheel/rail separation. The wheel/rail vertical forces would increase when the passing frequency of polygon is closed to the frequency coupled wheel/track resonance mode. Furthermore, the resonance of the axle box increases axle box acceleration. The wheelset axle stress is mainly influenced by the coupled wheel/track resonance mode and wheelset bending modes.

rigid-flexible dynamic model；coupled vehicle-track dynamic model；wheel polygonal wear；wheel/rail vertical forces；wheelset axle stress

U270.1

A

10.3969/j.issn.1006-0316.2020.05.011

1006－0316 (2020) 05－0067－08

2019－12－05

張國平（1986－），四川南充人，工程師，主要研究方向為機車車輛轉向架設計。*通訊作者：蔡吳斌（1991－），男，江蘇無錫人，博士研究生，主要研究方向為鐵道車輛系統動力學，Email：wubin0410@hotmail.com。