基于Hanning Window 設(shè)計FIR 數(shù)字高通濾波器*

陳紹榮，徐 舜，沈建國，朱行濤

（陸軍工程大學通信士官學校，重慶 400035）

0 引 言

一般有限沖激響應(yīng)(FIR)數(shù)字濾波器均要求設(shè)計成具有線性相位。國內(nèi)《數(shù)字信號處理》著作[1-3]， 對四種線性相位濾波器的頻率特性，均是先研究有限長對稱序列的z變換及其零極點分布，再研究有限長對稱序列在單位圓周上的z變換具有的特征，即序列的傅里葉變換具有的特征，其過程十分冗長。基于著作[4]，本文提出了一種研究線性相位FIR數(shù)字濾波器幅度函數(shù)的簡潔方法，首先揭示了偶對稱和奇對稱的線性相位FIR數(shù)字濾波器幅度函數(shù)的特點，然后研究了矩形窗函數(shù)對線性相位理想數(shù)字低通濾波器幅頻特性的影響，最后介紹了利用Hanning Window 來設(shè)計FIR數(shù)字高通濾波器的步驟及方法。

1 線性相位FIR 數(shù)字濾波器幅度函數(shù)的特點

1.1 實序列的傅里葉變換具有的特征

序列h(n)的傅里葉變換定義為：

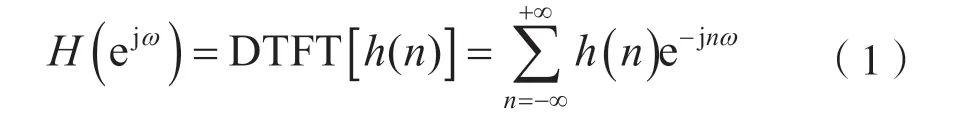
式（1）表明，一個序列h(n)的傅里葉變換H(ejω)是一個周期為2π的周期函數(shù)。通常將區(qū)間[-π,π] 稱為H(ejω)的主值區(qū)間。

若序列h(n)為實序列，則有：

考慮到式（2），由式（1）可得：

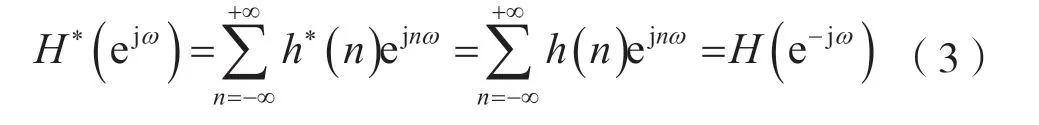
式（3）表明，實序列的傅里葉變換具有的特征是：實序列的傅里葉變換的反褶與傅里葉變換取共軛等價。

1.2 線性相位條件

（1）偶對稱情況

若FIR數(shù)字濾波器的單位沖激響應(yīng)h(n)是n定義在0 ≤n≤N-1 的N點長序列，并且滿足：

由于h(0)=h(N-1)，h(1)=h(N-2)，…，因此，稱h(n)為偶對稱序列，并將n=(N-1)/2 稱為偶對稱軸。

若h(n)是實序列，對式（4）兩邊取DTFT，并注意到式（3），則FIR數(shù)字濾波器的頻率特性可寫成：

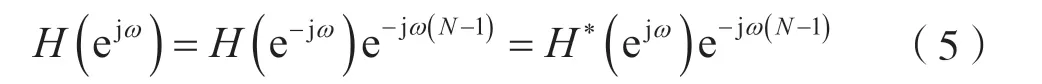
記：

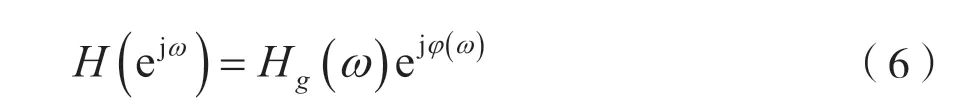
式中，Hg(ω)稱為幅度函數(shù)，φ(ω)稱為相位函數(shù)。注意，這里的Hg(ω)是ω的實函數(shù)，可為正值，也可為負值，即Hg(ω)=±|H(ejω)|。

考慮到式（6），則式（5）可寫成：

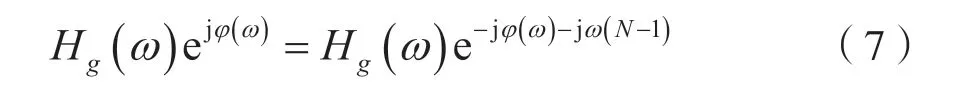
由式（7）可得：

由式（8）可得線性相位函數(shù)，即：

將式（9）代入式（6），可得FIR數(shù)字濾波器的頻率特性，即：

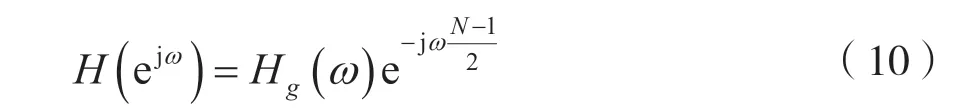
（2）奇對稱情況

若FIR數(shù)字濾波器的單位沖激響應(yīng)h(n)是n定義在0 ≤n≤N-1 的N點長序列，并且滿足：

由于h(0)=-h(N-1)，h(1)=-h(N-2)，…，因此，稱h(n)為奇對稱序列，并將n=(N-1)/2稱為奇對稱軸。

若h(n)是實序列，對式（11）兩邊取DTFT，并注意到式（3），則FIR數(shù)字濾波器的頻率特性可寫成：

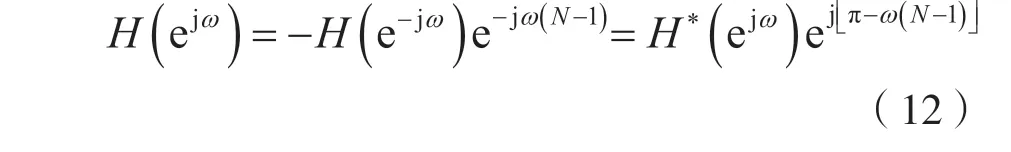
記：

考慮到式（13），則式（12）可寫成：

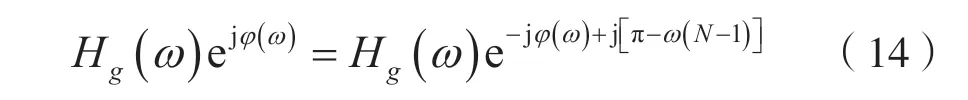
由式（14）可得：

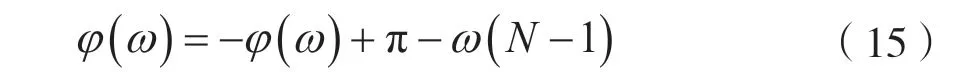
由式（15）可得線性相位函數(shù)，即：

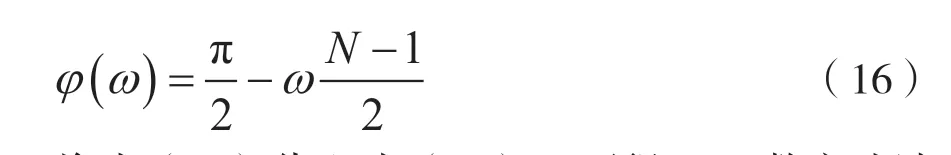
將式（16）代入式（13），可得FIR數(shù)字濾波器的頻率特性，即：

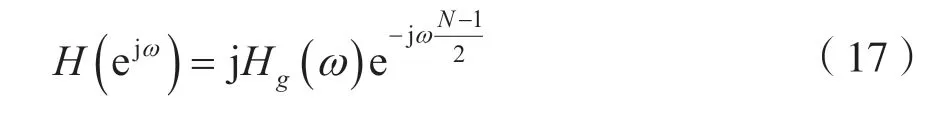
1.3 偶對稱線性相位數(shù)字濾波器幅度函數(shù)的特點

考慮到式（10），則有：

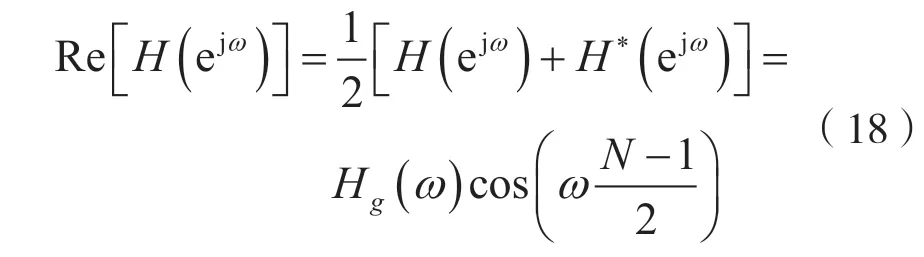
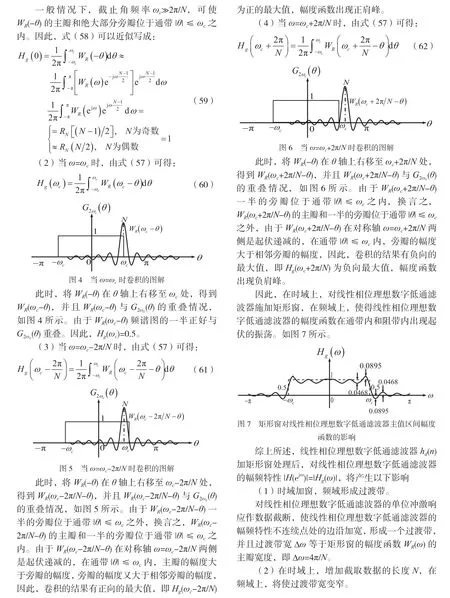
考慮到式（74）及式（75），并注意到WR(ω)為偶函數(shù)，由式（77）可得：

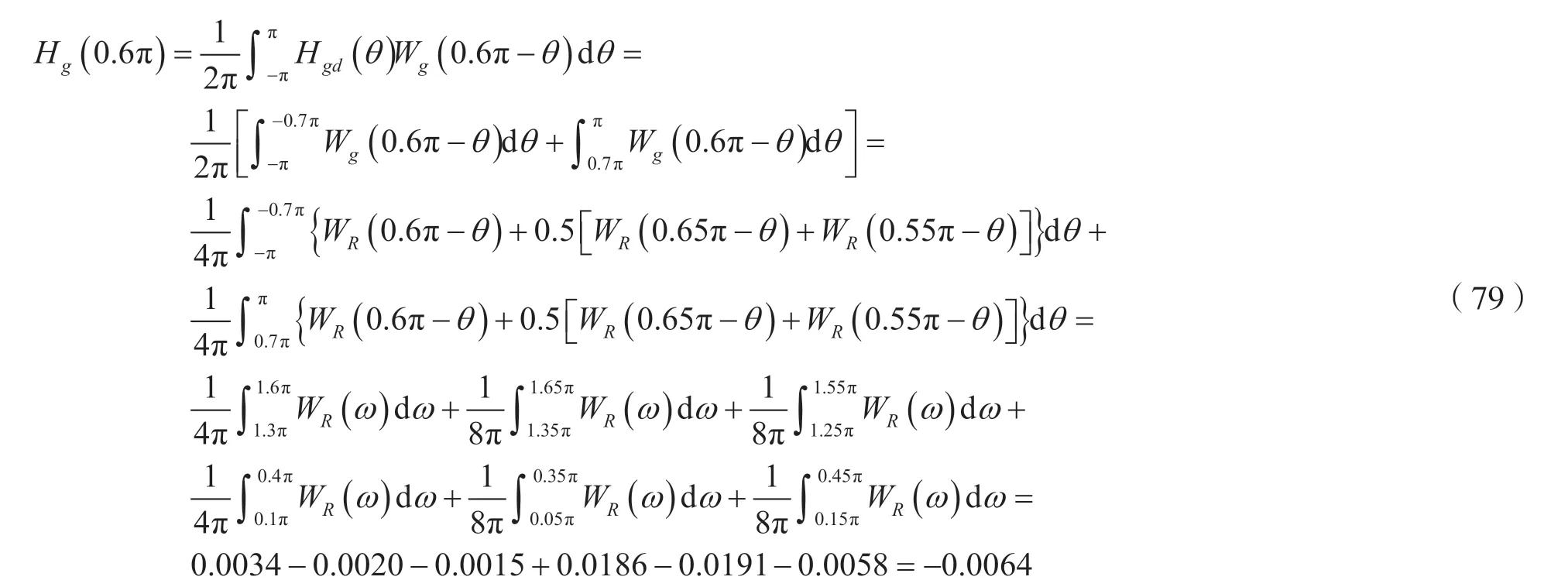
于是：

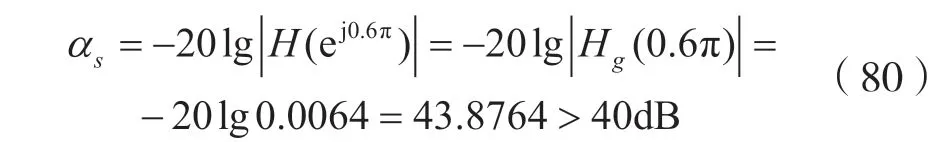
由式（80）可知，所設(shè)計的線性相位FIR 數(shù)字高通濾波器滿足阻帶最小衰減指標的要求。

4 結(jié) 語

本文提出了一種研究線性相位FIR 數(shù)字濾波器幅度函數(shù)的簡潔方法。首先揭示了偶對稱和奇對稱的線性相位FIR 數(shù)字濾波器幅度函數(shù)的特點；然后研究了矩形窗函數(shù)對線性相位理想數(shù)字低通濾波器幅頻特性的影響，并得到了一些有益的結(jié)論；最后給出了基于Hanning Window 來設(shè)計線性相位FIR數(shù)字高通濾波器的實例。