一種基于OPRA4方向關系推理定性距離變化的方法

董軼群 劉建東 徐文星 王淑鴻

(北京石油化工學院信息工程學院 北京 102617)

定性空間推理是人工智能的重要組成部分[1-4]，在基于內容的圖像檢索[5]、生物信息學[6]、地理信息系統[7]、智能交通[8-9]、空間數據庫[10]等領域中有著廣泛應用.面向拓撲[10-14]、方向[15-24]、距離[25]等單一方面空間關系的定性表示與推理研究已經非常深入.然而采用單一空間關系難以對復雜的空間信息進行有效處理.例如在智能交通領域中通常需要綜合路網拓撲信息、交通對象的移動方向以及彼此間的距離信息展開相關應用.因此結合2種以及2種以上空間關系的表示與推理成為近年來的研究熱點[26-36].

空間位置信息的有效表示與推理通常需要結合方向和距離關系.在定性方向與距離關系的結合研究方面已取得一些研究成果.Clementini等人[26]面向點對象，以參考對象為圓心，用若干個同心圓對二維平面空間進行不同粒度地劃分，通過主對象在參照框架中的分布情況來描述其相對于參照對象的定性距離關系，進而給出了距離系統的形式化定義；在該模型的基礎上，將定性方向與距離關系相結合用于描述空間對象間的相對位置關系，并研究了該位置關系上的復合運算.Frank[32]提出了一種能夠統一描述點對象間“東”、“南”、“西”、“北”方向關系與“遠”、“近”距離關系的定性表示模型，并研究了該模型上的復合運算與逆運算性質.王中輝等人[33]面向簡單區域對象，將8方向錐形模型與距離關系相結合，提出一種能夠同時描述定性方向與距離關系的表示模型；并在該模型基礎上利用四叉樹索引與最小邊界矩形提出一種基于方向與距離關系的復合空間查詢算法.許小艷[34]面向點對象提出一種基于錐形與距離劃分相結合的表示模型，該模型能夠統一描述定性方向與距離關系；利用定性三角形推理方法，通過三角形的邊—角關系劃分定性角度值和距離值，在此基礎上研究了方向與距離關系的組合推理規則.Weghe等人[37]綜合考慮時間屬性、定性距離關系與十字方向關系，提出了定性軌跡演算(qualitative trajectory calculus, QTC).文獻[38-40]通過擴展QTC提出了定性直線投影演算(qualitative rectilinear projection calculus, QRPC)、點-軌跡定性軌跡演算(point-trajectory QTC, P-tQTC)等一系列面向平面軌跡對象的時空關系模型，然而此類模型中方向與距離的定性域多為{0,+,-}，難以描述復雜的實際問題.

現有定性方向與距離關系的結合研究多是面向靜態空間對象；側重2種關系的組合表示方法，通常利用方向關系對當前狀態下的距離關系進行推理，難以對后續的定性距離變化做出有效推斷.然而在眾多領域中，定性距離變化的分析與預測至關重要，是開展軌跡相似性分析、交通流量預測、時空數據庫連續查詢等空間位置相關理論與應用研究的重要基礎.例如在“連續查詢路網中距離某個用戶最近的k個移動對象”、“實時分析預測某一區域內的交通流量”等應用中，大規模的交通對象和連續的查詢請求對相關理論模型與應用系統提出了挑戰.利用方向關系首先篩選出“將接近”或“將遠離”用戶和區域的交通對象，然后再有針對性地進行定量距離計算，是提高算法性能、緩解系統計算壓力的一種有效途徑.然而這種基于移動對象間方向關系推理定性距離變化的研究尚不多見.

1 背景知識

在少數針對移動對象的方向關系模型中，OPRAm不僅表達能力強，同時還具備良好的復合運算與逆運算性質[17]，因此本文研究工作基于該模型展開.

1.1 OPRAm模型

OPRAm忽略空間對象的尺寸與維度，將一個移動的空間對象抽象為一個帶方向的點，稱為有向點，可以用一個序對進行表示：

S=(PS,φS),

(1)

其中，PS為S的位置，用S的坐標表示，即PS=(xS,yS);φS是從x軸正向逆時針旋轉到PS所形成的旋轉角，用以表示S的移動方向.該旋轉角取值區間是[0,2)上的循環群，例如-3與53相等.

定義1.給定粒度參數m∈+,有向點A,B之間的OPRAm關系ROPRAm(A,B)定義為

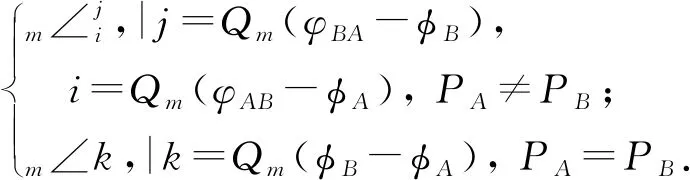
(2)

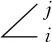
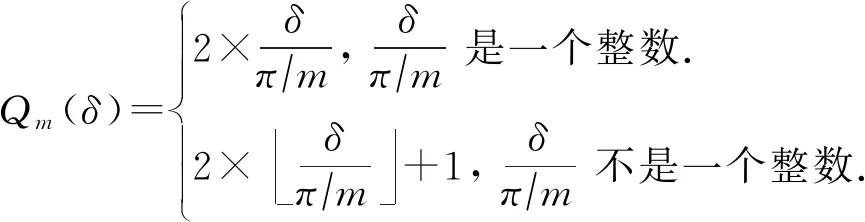
(3)

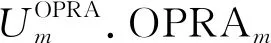
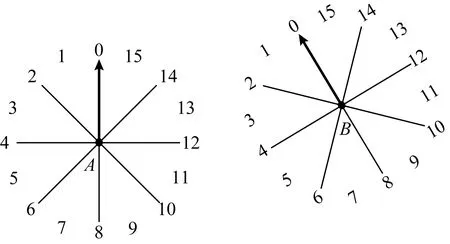
圖

由定義1,對于任意2個有向點A,B,在用OPRA4模型(即OPRAm的粒度參數m=4)描述二者方向關系時，首先將A視為參照對象，根據A的移動方向，采用4條以A為交點的直線對二維平面進行等分，確定A所對應的參照系統，其中包含了8個扇形區域、8條射線以及一個中心點，共17個部分；在此基礎上，將B作為主對象，根據B在A所確定的參照系統中的分布情況來描述B相對于A的方向.反之，采用同樣的方式可確定A相對于B的方向；最后綜合二者之間的相對方向，得到A,B之間的基本OPRA4方向關系.按照上述方式，若PA≠PB,則A,B間存在256種基本OPRA4方向關系；特殊地，若PA=PB,則A,B間存在16種基本OPRA4方向關系，因此共有272種基本OPRA4方向關系.若干基本OPRA4方向關系構成的一個非空集合稱為OPRA4方向關系.

1.2 定性距離變化

距離是一種重要的空間信息，常見的有歐氏距離、閔可夫斯基距離和曼哈頓距離等，這些都是對距離的定量度量方式.然而精準的定量距離信息通常難以甚至無法獲得；而且在許多應用場景中，尤其是一些具有流式計算或實時性需求的場景中，通常需要定性距離或定性距離變化作為后續數據分析與處理的依據.

以“連續查詢路網中距離用戶A最近的3輛出租車”應用場景為例，在此連續查詢過程中，若每一次查詢時對所有出租車到用戶A的距離進行計算后排序，那么隨著出租車數量與查詢頻率的增加，系統將面臨巨大的計算壓力，很難滿足實時性需求.若每一次查詢前，首先基于方向關系對出租車與用戶A之間的定性距離變化進行推理，篩選出距離“將變小”的出租車組成候選集合，然后再對候選集合內的出租車計算路網距離并排序，將有助于提高模型的有效性與系統的執行效率.

本文面向二維平面空間中移動的點對象，考慮對象間的歐氏距離，將定性距離變化分為“變大”、“變小”、“不變”和“不確定”共4種情況.本文著重研究OPRA4方向關系對這4種定性距離變化的約束作用.

2 OPRA4對定性距離變化的約束

2.1 移動對象間的相對位置關系Rpos-pair

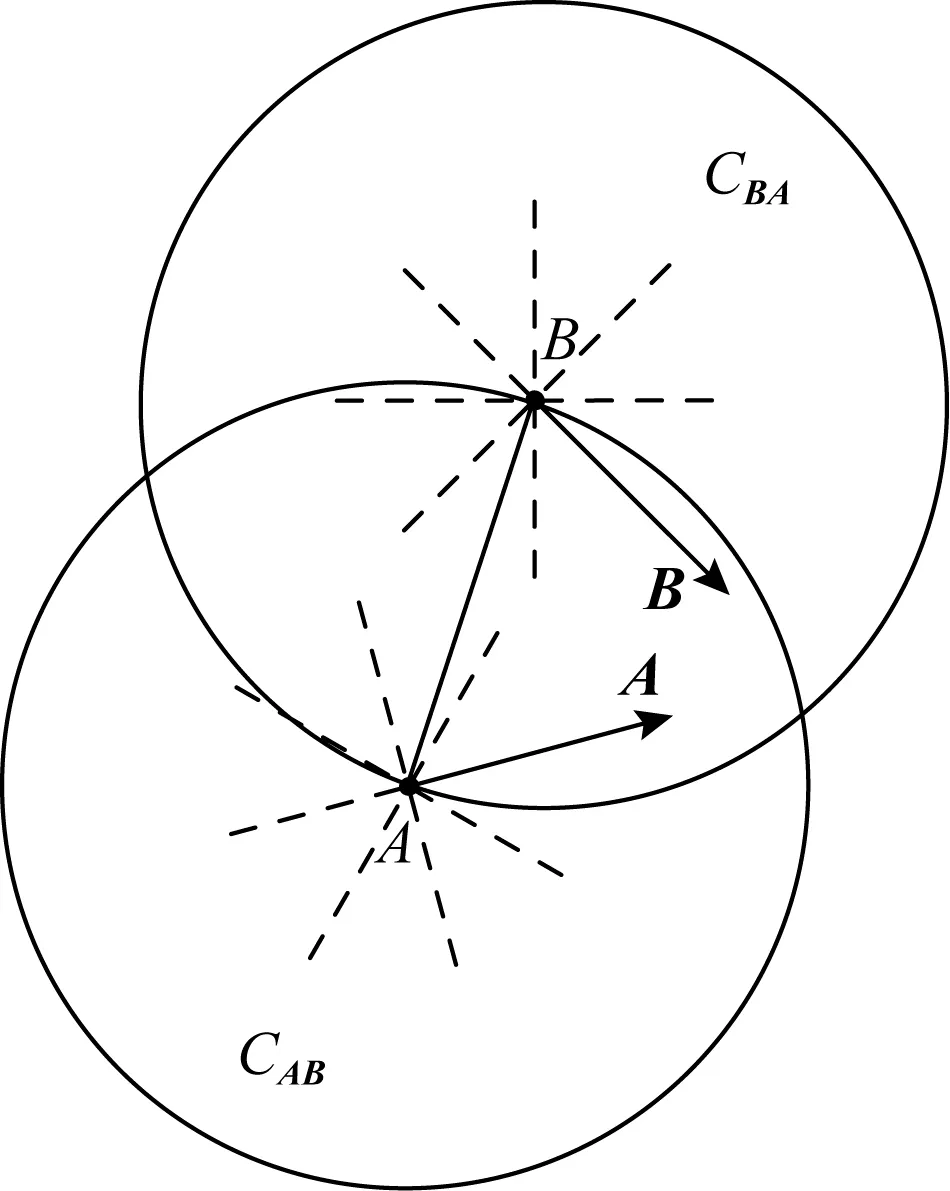
Fig. 2 The spatial positions of A and CBA,B and CAB圖2 A與CBA，B與CAB的空間位置示例圖

對于有向點A=(PA,φA)與B=(PB,φB),用A,B分別表示以A,B為起點的射線；用AB表示以A為起點、B為終點的一條有向線段；用CAB表示以A為圓心，以A與B之間的歐氏距離(|AB|)為半徑的圓.不難發現，在A,B移動過程中，A與CBA以及B與CAB的空間位置在一定程度上能夠反映出二者之間距離的變化趨勢.例如在圖2中，若不考慮靜止情況，A,B分別沿著各自當前方向移動某一微小時間間隔后，二者之間距離將變小.

為了系統研究這種空間位置與定性距離變化的約束作用，首先參照直線與圓的位置關系，根據A到B的投影情況來定義B與CAB之間的位置關系.

定義2.對于有向點A=(PA,φA)與B=(PB,φB),PA≠PB,將A向B所在直線投影得投影點Proj(A),若|AProj(A)|=|AB|,即Proj(A)=B,則稱B與CAB相切，記為q(B,CAB).

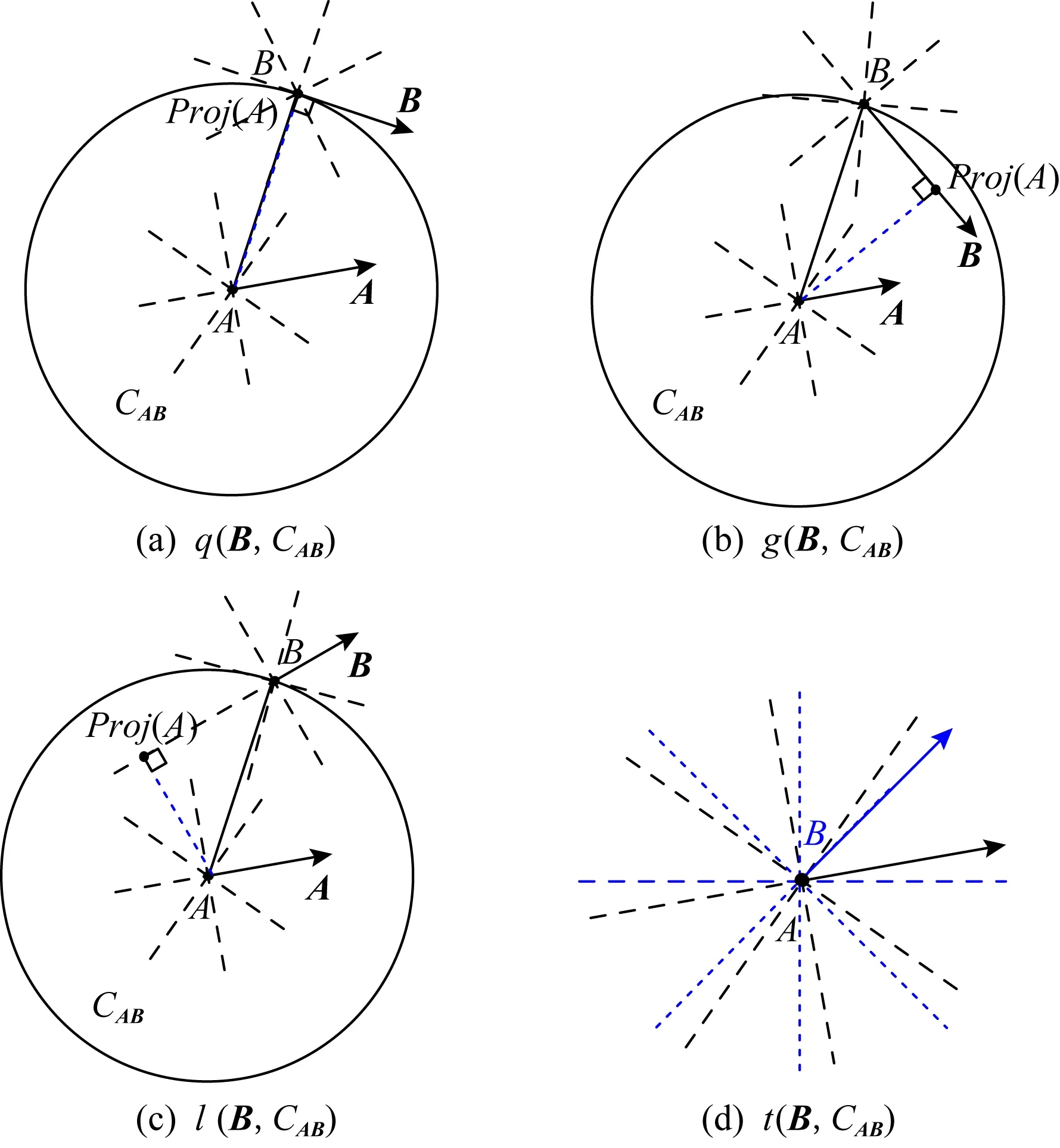
Fig. 3 The possible position relations between B and CAB圖3 B與CAB之間可能的位置關系

定義3.對于有向點A=(PA,φA)與B=(PB,φB),PA≠PB,將A向B所在直線投影得投影點Proj(A),若|AProj(A)|<|AB|且Proj(A)∈B,則稱B與CAB相割，記為g(B,CAB).

定義4.對于有向點A=(PA,φA)與B=(PB,φB),PA≠PB,將A向B所在直線投影得投影點Proj(A),若|AProj(A)|<|AB|且Proj(A)B,則稱B與CAB相離，記為l(B,CAB).

特殊地，當PA=PB時，即有向點A,B坐標重合，有|AB|=0,此時圓CAB相當于一點，用定義5來描述這種特殊情況.

定義5.對于有向點A=(PA,φA)與B=(PB,φB),若PA=PB,則稱B與CAB同置，記為t(B,CAB).

很顯然，若t(B,CAB)則必然有t(A,CBA).

定義2～5對應的4種關系分別如圖3(a)～(d)所示.

定義6.對于任意2個有向點A,B,由B與CAB之間的位置關系所構成的集合記為Rpos,則有：

Rpos={q,g,l,t},

(4)

稱Rpos中的每一個元素為一個基本Rpos關系.

定理1.關系集合Rpos是完備互斥的.

證明. 對于二維平面中任意2個有向點A,B,若二者坐標不同，則Proj(A)與射線B必定滿足3種可能的位置關系(Proj(A)=B,|AProj(A)|<|AB|且Proj(A)∈B,|AProj(A)|<|AB|且Proj(A)B)中的一種，由上述定義2～4可知，對應的B與CAB之間必定滿足3種關系q,g,l中的一種；若A,B坐標相同，則由定義5可知對應的B與CAB之間滿足關系t.因此任意2個有向點A,B之間必定滿足一種基本Rpos關系且僅滿足一種，即關系集合Rpos是完備互斥的.

證畢.

為了更加全面準確地描述任意2個有向點A,B之間的空間信息，不僅要明確B與CAB之間的位置關系，還要明確A與CBA之間的位置關系.

定義7.Rpos-pair為Rpos上的一個有序二元關系，定義為

Rpos-pair={g,g,g,q,g,l,q,g,q,q,
q,l,l,g,l,q,l,l,t,t}，

(5)

稱Rpos-pair中每一個元素為一個基本Rpos-pair關系.

利用Rpos-pair可描述有向點間的相對位置關系.對于任意2個有向點A,B,二者滿足一種基本Rpos-pair關系，其語義如表1所示：

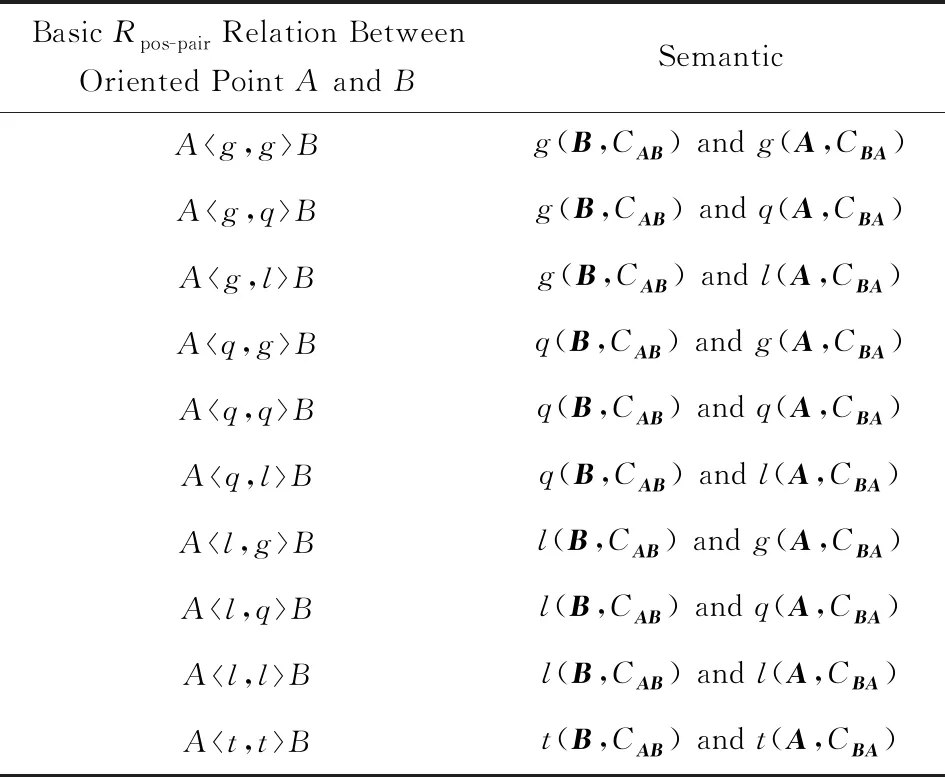
Table 1 The Semantic of Basic Rpos-pair Relations表1 基本Rpos-pair關系語義表

推論1.關系集合Rpos-pair是完備互斥的.

證明.Rpos上的二元關系最多包含16個元素，由定義5可知對于任意2個有向點A,B,若t(B,CAB)則t(A,CBA),即二者不存在6種相對位置關系：t,g,t,q,t,l,g,t,q,t,l,t;且定理1已證明集合Rpos是完備互斥的，因此A,B必定滿足Rpos-pair中10個關系中的一種且僅一種，即Rpos-pair也是完備互斥的.

證畢.

2.2 Rpos-pair對定性距離變化的約束

對于任意2個有向點A=(PA,φA)與B=(PB,φB),在不同基本Rpos關系下，φB與φAB之間滿足命題1～3.

命題1.對于任意2個有向點A=(PA,φA)與B=(PB,φB),若l(B,CAB),φAB∈[0,2π),則有φB∈(φAB-π2,φAB+π2).

證明. 當φAB∈[0,π2)時，如圖4所示，若l(B,CAB),由定義4可知Proj(A)應位于CAB上過B點切線的下方，基于平面幾何中角度間的關系易知φB∈(φAB-π2,φAB+π2).

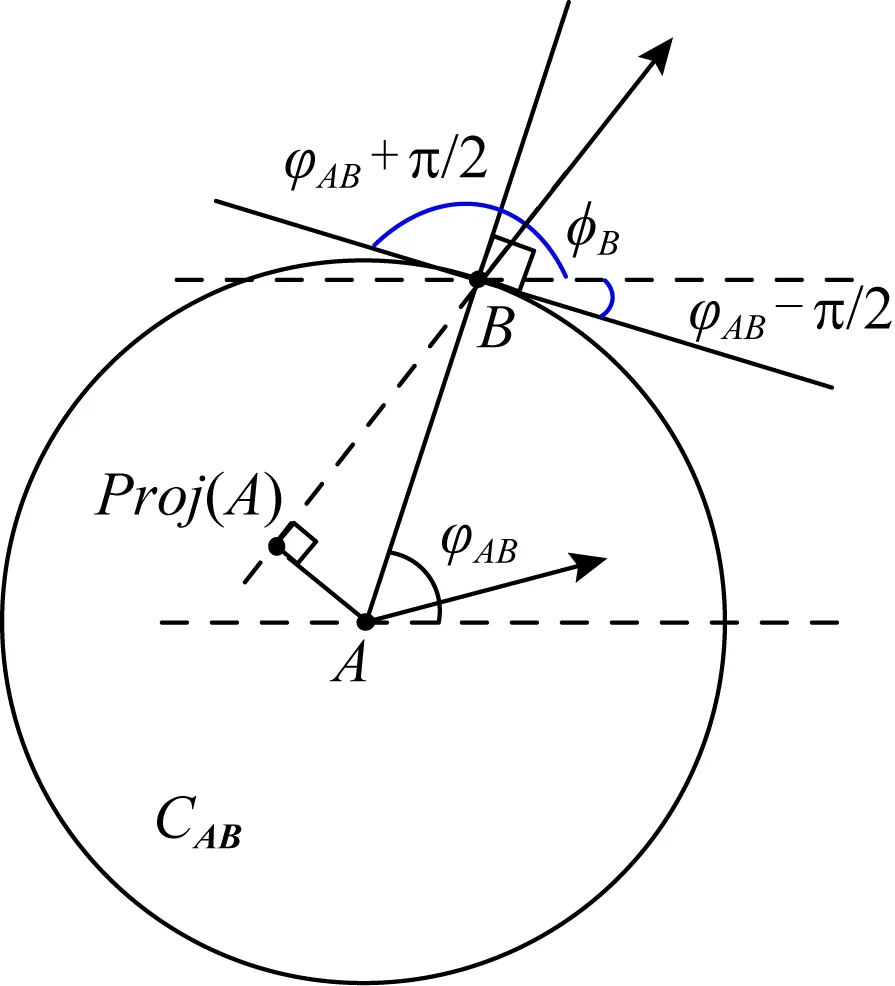
Fig. 4 The range of φBwhen l(B,CAB) and φAB∈[0,π2)圖4 l(B,CAB)且φAB∈[0,π2)時φB取值示例圖

類似地，若l(B,CAB),分別當φAB∈[π2,π),φAB∈[π,3π2),φAB∈[3π2,2π)時，均有φB∈(φAB-π2,φAB+π2).

證畢.

同理可證命題2與命題3成立.

命題2.對于任意2個有向點A=(PA,φA)與B=(PB,φB),若g(B,CAB),φAB∈[0,2π),則有φB∈(φAB+π2,φAB+3π2).

命題3.對于任意2個有向點A=(PA,φA)與B=(PB,φB),若q(B,CAB),φAB∈[0,2π),則有φB=φAB+(2k+1)π2,k∈.

不難發現，有向點A,B的移動方向、在各自方向上的移動距離、AB與x軸的夾角等因素均影響著二者之間后續的定性距離變化.下面通過定理2給出上述因素與定性距離變化之間的關系.

定理2.任意2個有向點A=(PA,φA)與B=(PB,φB),分別沿著各自方向移動LA,LB后到達A′=(PA′,φA),B′=(PB′,φB),若PA≠PB且A與CBA以及B與CAB之間不存在相切關系，當LA=LB=0時|A′B′|2的增量z滿足：

z≈-2((xB-xA)cosφA+
(yB-yA) sinφA)LA+2((xB-xA)cosφB+
(yB-yA)sinφB)LB,

(6)

其中,φA,φB,φAB∈[0,2π),PA=(xA,yA),PB=(xB,yB),PA′=(xA′,yA′),PB′=(xB′,yB′),LA≥0與LB≥0分別為一微小時間間隔內LA,LB的增量.

證明. 由2點間距離公式可知:

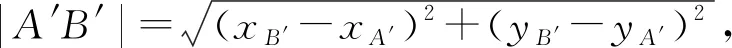
(7)

構造二元函數

z=f(LA,LB)=|A′B′|2,

(8)

將式(7)帶入式(8)有:

f(LA,LB)=(xB′-xA′)2+(yB′-yA′)2,

(9)

由于xB′=LBcosφB+xB,yB′=LBsinφB+yB,xA′=LAcosφA+xA,yA′=LAsinφA+yA,例如圖5所示:

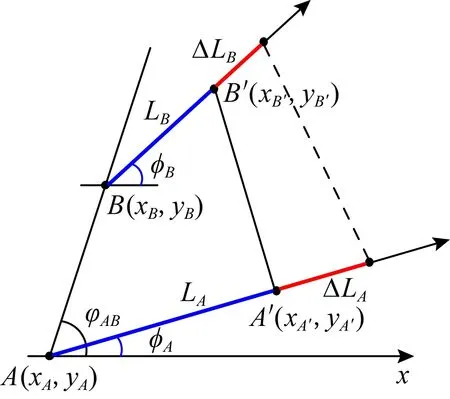
Fig. 5 The corresponding coordinates, angle and distances of A and B圖5 有向點A,B相關坐標、夾角、移動距離示例圖

因此有:

f(LA,LB)=(LBcosφB+xB-
LAcosφA-xA)2+
(LBsinφB+yB-LAsinφA-yA)2,

(10)

整理后有:

f(LA,LB)=(LBcosφB-LAcosφA)2+
(LBsinφB-LAsinφA)2+
2(LBcosφB-LAcosφA)(xB-xA)+
2(LBsinφB-LAsinφA)(yB-yA)+
(xB-xA)2+(yB-yA)2.

(11)

函數f(LA,LB)描述了有向點A,B沿著各自方向移動的距離(分別為LA,LB)與A,B移動后二者間距離(即|A′B′|)之間的關系.對f(LA,LB)求一階偏導數有:

fLA=2(LA-LBcos(φA-φB)-
(xB-xA)cosφA-(yB-yA)sinφA),

(12)

fLB=2(LB-LAcos(φA-φB)+
(xB-xA)cosφB+(yB-yA)sinφB),

(13)

因此f(LA,LB)在LA=LB=0處的全增量z滿足:

z≈dz=-2((xB-xA)cosφA+
(yB-yA)sinφA)LA+2((xB-xA)cosφB+
(yB-yA)sinφB)LB.

(14)

若PA=PB,則xB=xA,yB=yA,此時無論φA,φB,LA與LB如何取值，式(14)中z恒為0.這意味著在微小時間間隔內，z無法準確表示有向點A,B間的距離增量.

若PA≠PB且xB=xA,則yB≠yA.當q(A,CBA)時,必有φA=k,k∈Z,因此sinφA=0,使得無論LA如何取值，式(14)中LA系數恒為0.這意味著無論有向點A如何移動，式(14)中z無法準確描述LA對A,B間距離增量的約束作用.

若PA≠PB且xB≠xA,式(14)可進一步整理為

z≈-2(cosφA+tanφABsinφA)(xB-xA)LA+
2(cosφB+tanφABsinφB)(xB-xA)LB.

(15)

當q(A,CBA)時,由命題3可知φA=φBA+(2k+1)π2,k∈Z,由于φBA=φAB+π,因此φAB-φA=-(2k+3)π2,k∈Z,即cos(φAB-φA)=0.根據三角函數和差公式可知cosφABcosφA+sinφABsinφA=0,即cosφA=-tanφABsinφA,使得無論LA如何取值，式(15)中LA系數恒為0,即式(15)中z無法準確描述LA對A,B間距離增量的約束作用.同理，q(B,CAB)時情況類似.

證畢.

本文將利用定理2研究任意2個有向點在不同基本Rpos-pair關系下的定性距離變化.

推論2.對于任意2個有向點A,B,若Ag,gB,在A,B分別沿著各自當前方向移動某一微小時間間隔后，二者之間距離將不變或變小.

證明. 設A,B分別沿著各自當前方向移動了LA,LB到達A′,B′,經過某一微小時間間隔后到達A″,B″,期間LA,LB的增量分別為LA≥0與LB≥0.已知Ag,gB,當LA=LB=0時基于定理2中式(6)對LA,LB分情況討論：

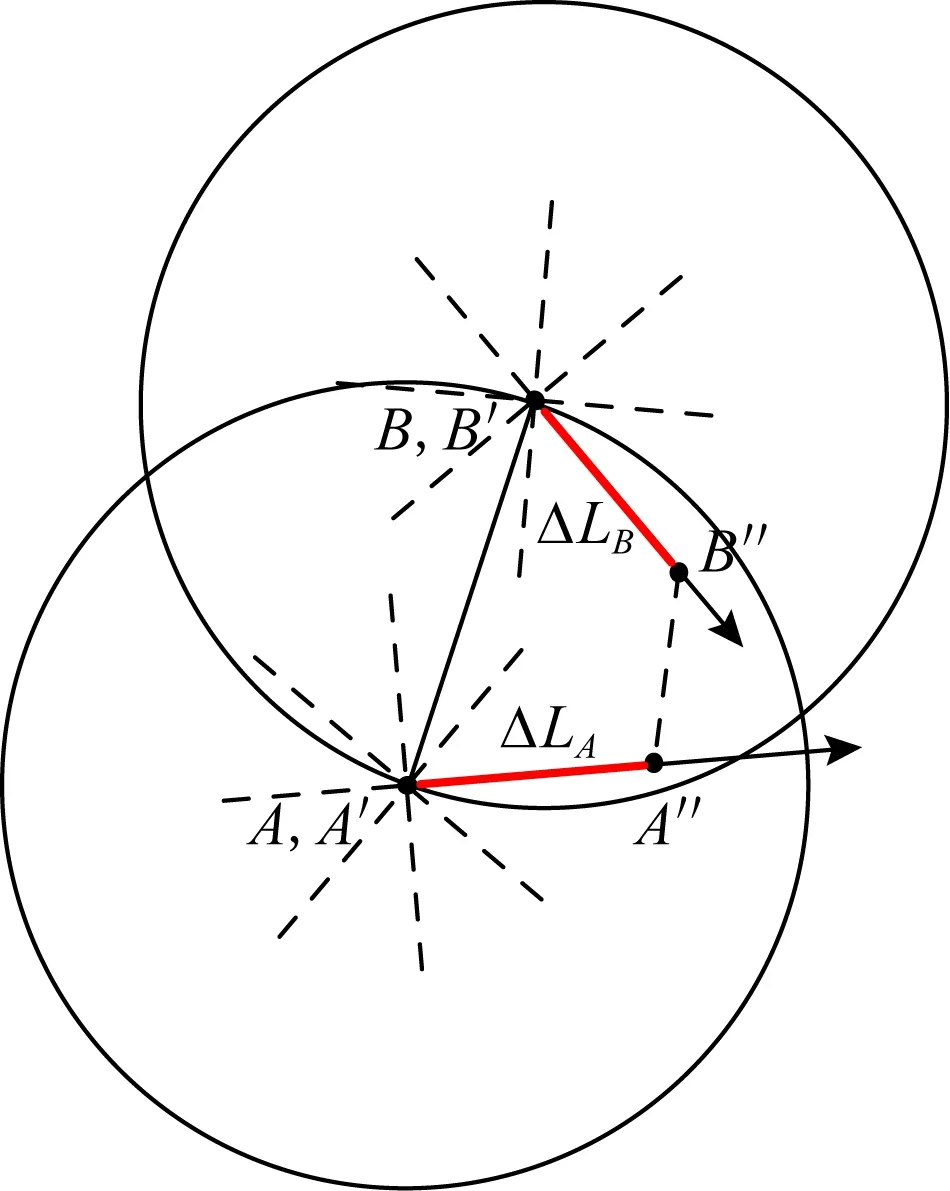
Fig. 6 Ag,gB and LA=LB=0圖6 Ag,gB且LA=LB=0示例圖

綜上所述，若Ag,gB,在一微小時間間隔內A,B沿著當前方向移動，若至少一方移動的距離不為0，則二者之間距離將變小；若二者移動距離均為0，則二者之間距離將不變.

證畢.

推論3.對于任意2個有向點A,B,若Al,lB,在A,B分別沿著各自當前方向移動某一微小時間間隔后，二者之間距離將不變或變大.

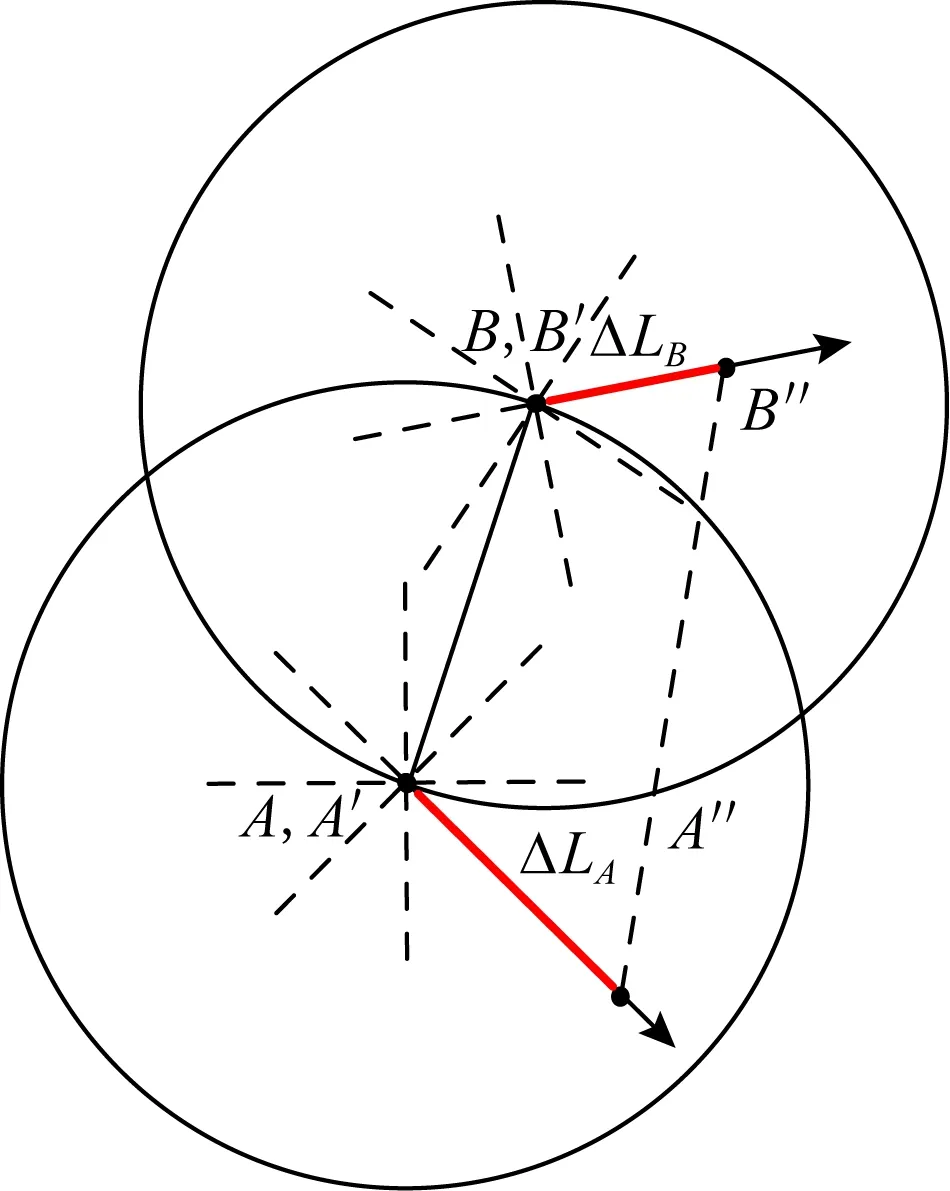
Fig. 7 Al,lB and LA=LB=0圖7 Al,lB且LA=LB=0示例圖

綜上所述，若Al,lB,在一微小時間間隔內A,B沿著當前方向移動，若至少一方移動的距離不為0,則二者之間距離將變大；若二者移動距離均為0,則二者之間距離將不變.

證畢.

在Rpos描述的位置關系中，相切作為相割、相離之間的鄰接關系，其情況比較特殊.對于有向點A,B,若A與CBA或B與CAB之間存在相切關系，那么二者移動過程中的距離變化更加復雜，無法完全適用定理2,一些情況需要單獨討論.

推論4.對于任意2個有向點A,B,若Ag,qB或Aq,gB,則在A,B分別沿著各自當前方向移動某一微小時間間隔后，二者之間距離變化不確定.

證明. 當Ag,qB時，設A,B分別沿著各自當前方向移動了LA,LB到達A′,B′,經過某一微小時間間隔后到達A″,B″,期間LA,LB的增量分別為LA≥0與LB≥0.對LA,LB分情況討論：

1) 與定理2中式(14)之前的證明部分相同，已知Ag,qB,因此有PA≠PB,g(B,CAB).若limLA=0,limLB≠0,此時與推論2中的情況1證明相同，可知二者之間距離將變小.

2) 已知q(A,CBA),在證明定理2時已說明，此時cos(φAB-φA)=0,使得式(14)中LA的系數恒為0,無法用式(14)討論距離變化.當PA≠PB,LA=LB=0時，可知B′=B,A′=A,|A′B′|=|AB|;當limLB=0,limLA≠0時，可知B″與B′近似相等，如圖8所示，因此有|A″B″|≈|A″B′|.根據致直角三角形斜邊大于直角邊可知|A″B″|>|A′B′|,進而有|A″B″|>|AB|,因此二者之間距離將變大.

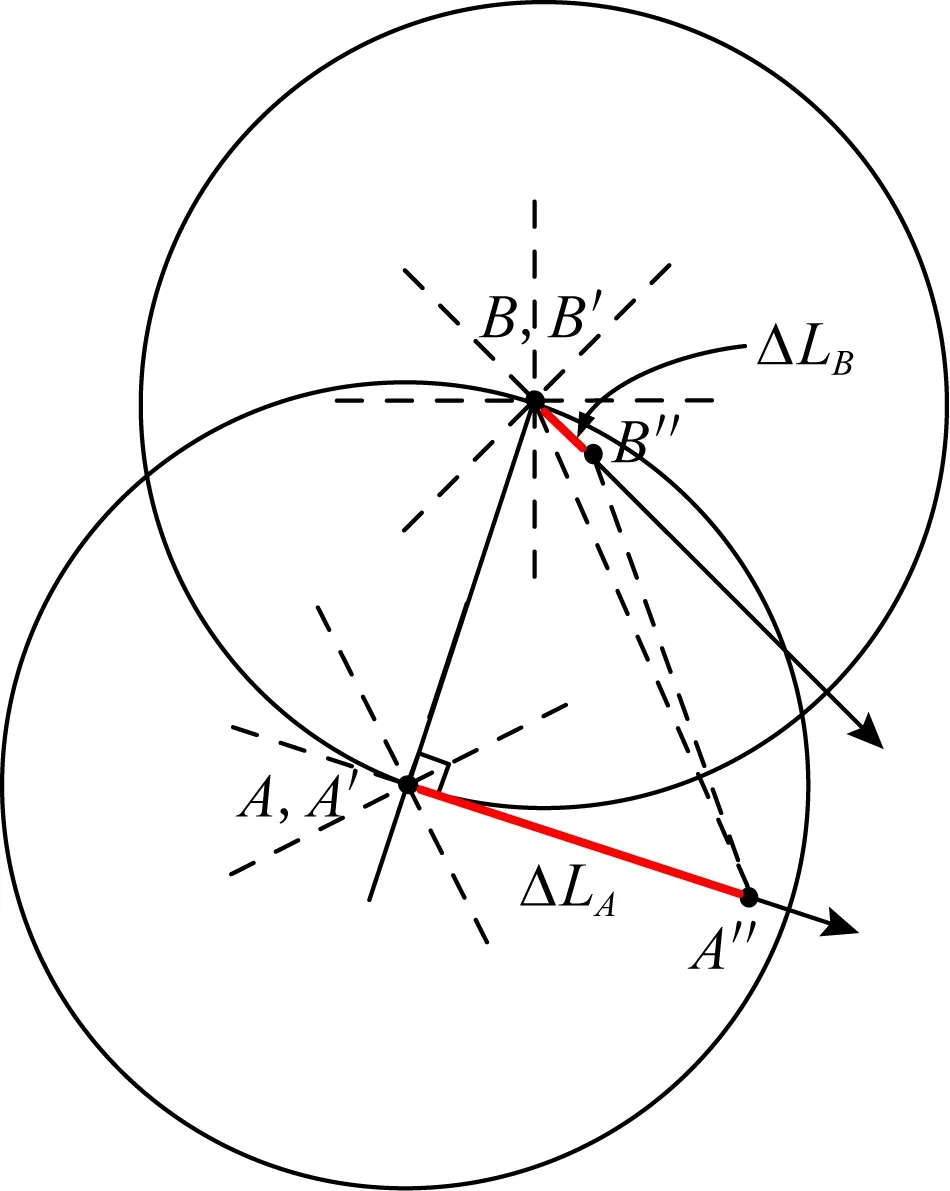
Fig. 8 Ag,qB,lim LB=0 and lim LA≠0圖8 Ag,qB,lim LB=0且lim LA≠0示例圖

綜上所述，若Ag,qB在微小時間間隔內A,B分別沿著各自當前方向移動距離的不同情況可能導致二者之間的距離變小、變大或者是不變，因此無法確定二者之間的距離變化.

同理可證，當Aq,gB時，A,B之間距離變化不確定.

證畢.

類似地，基于定理2可證明推論5～7成立.

推論5.對于任意2個有向點A,B,若Ag,lB或Al,gB,在A,B分別沿著各自當前方向移動某一微小時間間隔后，二者之間距離變化不確定.

推論6.對于任意2個有向點A,B,若Al,qB或Aq,lB,在A,B分別沿著各自當前方向移動某一微小時間間隔后，二者之間距離將不變或變大.

推論7.對于任意2個有向點A,B,若Aq,qB,在A,B分別沿著各自當前方向移動某一微小時間間隔后，二者之間距離將不變或變大.

特殊地，當2個有向點對應的射線與圓存在同置關系時，二者之間的距離變化如定理3所述.

定理3.對于任意2個有向點A,B,若At,tB,在A,B分別沿著各自當前方向移動某一微小時間間隔后，二者之間距離將不變或變大.

證明. 當有向點A,B對應的射線與圓存在同置關系時，根據定義5有PA=PB,如圖3(d)所示，若二者的移動方向與速度均相同，則二者之間距離保持不變；若二者移動方向或速度不同，則二者之間距離必將變大.

證畢.

在證明定理2、定理3以及推論2～7的過程中，將微小時間間隔內有向點的靜止狀態視為移動過程中的一種特殊狀態，因此本文面向移動對象提出的理論模型同樣適用于靜止對象間、靜止對象與移動對象間的方向與距離關系結合推理.

2.3 Rpos-pair與OPRA4的對應關系

首先通過命題4～7研究基本Rpos關系與OPRA4方向關系之間的對應關系；然后給出基本Rpos-pair關系與OPRA4方向關系之間的對應關系.

證明. 由命題1可知，對任意2個有向點A,B,若l(B,CAB),則有φB∈(φAB-π2,φAB+π2).令δ=(φBA-φB),由式(2)可知j=Qm(δ);由于φBA=φAB+π,因此δ∈(π2,3π2),由式(3)可知j∈{5,6,7,8,9,10,11}.

證畢.

與命題4的證明過程類似，可證命題5與命題6成立.

命題7.對于任意2個有向點A,B,若t(B,CAB),則A4∠kB,其中k∈{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}.

證明. 由定義5可知，若有向點A,B對應的射線與圓之間存在同置關系，則有PA=PB,進而由定義1可知A4∠kB,其中k∈{0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}.

證畢.

通過上述命題4～7可歸納出基本Rpos關系與OPRA4方向關系之間的對應表，如表2所示；在此基礎上，通過組合方式可進一步得到基本Rpos-pair關系與OPRA4方向關系之間的對應關系，如表3所示.

Table 2 Corresponding Table of Basic Rpos Relations and OPRA4 Direction Relations

Table 3 Corresponding Table of Basic Rpos-pair Relations and OPRA4 Direction Relations表3 基本Rpos-pai與OPRA4方向關系對應表

2.4 OPRA4對定性距離變化的約束

對于任意2個有向點A,B,本文2.2節給出了A,B間基本Rpos-pair關系對二者間定性距離變化的約束作用；2.3節明確了A,B間基本Rpos-pair關系與二者間OPRA4方向關系的對應關系.因此借助于基本Rpos-pair關系可以建立起OPRA4方向關系與定性距離變化的內在聯系，如表4所示.

表4相當于給出了OPRA4方向關系全集的一個劃分：

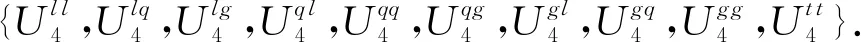
(16)

Table 4 Corresponding Table of OPRA4 Direction Relations and Qualitative Distance Changes表4 OPRA4方向關系與定性距離變化對應表

對于任意2個有向點A,B,二者滿足的基本OPRA4方向關系必定屬于該劃分中的某個子集且僅屬于一個子集.因此，當已知A,B之間的基本OPRA4方向關系時，可以參照表4對二者之間定性距離變化進行相應的判斷.

3 基于OPRA4推理定性距離變化算法與實例

為方便形式化表示與說明，將二維平面中2個有向點間的4種定性距離變化“變大”、“變小”、“不變”、“不確定”分別用further,nearer,unchange,uncertain表示，構成的集合記為Udis,則有：

Udis={further,nearer,unchange,uncertain}.

(17)

下面給出算法1是OPRA4-Distance的偽代碼對于任意2個有向點，當已知二者當前基本OPRA4方向關系時，用該算法對微小時間間隔內二者基于Udis的定性距離變化進行推斷.

算法1.OPRA4-Distance.

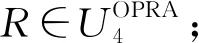
輸出：有向點A,B間的定性距離變化D∈2Udis.

①D←;

③ if(((i≥4 andi≤12) and (j≥5 andj≤11)) or ((i≥4 andi≤12) and (j=4 orj=12)))

④D←{unchange,further};

⑤ end if

⑥ if((((i≥0 andi≤3) or (i≥13 andi≤15)) and (j≥4 andj≤12)) or (((j≥0 andj≤3) or (j≥13 andj≤15)) and (i≥4 andi≤12)))

⑦D←{uncertain};

⑧ end if

⑨ if(((i≥0 andi≤3) or (i≥13 andi≤15)) and ((j≥0 andj≤3) or (j≥13 andj≤15)))

⑩D←{unchange,nearer};

定理4.對于任意2個有向點A,B,若已知二者間的基本OPRA4方向關系,算法OPRA4-Distance能夠正確推斷出后續微小時間間隔內二者間基于Udis的定性距離變化.

證明. 設有向點A,B滿足基本OPRA4方向關系R.

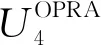
證畢.

以智能交通中的“連續k近鄰查詢”問題為例介紹本文理論模型的具體應用.

例1.如圖9所示，時刻ti與tj路網中有A,B1,B2,B3,B4,B5,B6共7個移動對象，以A作為查詢對象，連續查詢距離A最近的2個移動對象.路網中移動對象與道路邊交點間的數值表示距離，tj=ti+t,t為某一微小時間間隔.

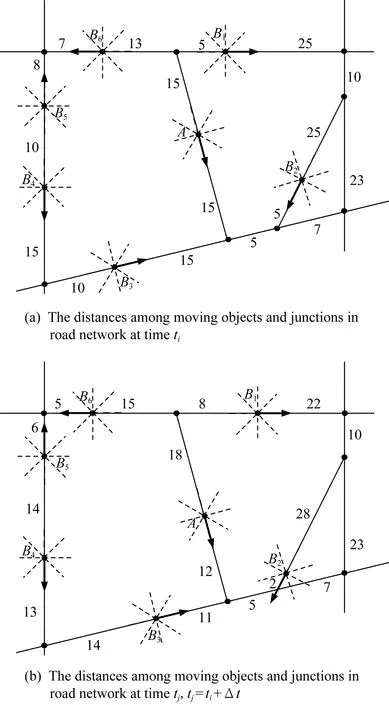
Fig. 9 An example of moving objects in a road network from time tito tj圖9 路網中移動對象距離變化示例

針對例1，首先將連續k近鄰查詢轉換為以t為周期的周期式查詢.下面通過算法OPRA4-Distance-Candidate給出基于OPRA4和定性距離變化篩選移動對象候選集的方法，其中q為查詢對象，R為基本OPRA4方向關系，Dis∈2Udis為定性距離變化集，Candidate為當前查詢過程中確定的初始移動對象候選集，ResultKNN為上一次查詢結果，CandidateKNN為當前查詢過程中基于OPRA4和定性距離變化篩選后的移動對象候選集.

算法2.OPRA4-Distance-Candidate.

輸入：Candidate,ResultKNN;

輸出：CandidateKNN.

① for eachpinCandidate

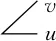
③Dis=OPRA4-Distance(R);

④ if (Dis={unchanged,further})

⑤Candidate=Candidate-{p};

⑥ end if

⑦ end for

⑧CandidateKNN=Candidate∪ResultKNN.

在智能交通領域中，不同的連續k近鄰查詢方法在路網與移動對象的建模、索引結構設計、地圖匹配策略、對象間距離的計算、路段與移動對象候選集的確定等環節采用了不同的方法.算法2主要針對移動對象候選集的確定環節.在例1中，為方便說明，設時刻ti查詢確定的CandidateKNN={B1,B2,B3,B4,B5,B6},計算B1～B6各點到A的路網距離后排序，可知時刻ti查詢結果ResultKNN={B1,B2},如圖9(a)所示.經過t后到達時刻tj，首先確定時刻tj查詢的Candidate(不同連續k近鄰查詢方法中確定移動對象候選集的方式不盡相同，此處不做詳細討論)，為方便說明，設Candidate={B1,B2,B3,B4,B5,B6}.由圖9(b)和語句①②可知在時刻tj,Candidate中各移動對象與A之間分別滿足如下基本OPRA4方向關系：此時基于語句③可知，B2,B3與A的距離將不變或變小；B1,B5,B6與A的距離不變或變大；B4與A的距離變化不確定.由于路網中兩點間的歐氏距離小于等于路網距離，因此經由語句④⑤篩選后可確定Candidate={B2,B3,B4}.由于以微小時間間隔為查詢周期，因此上一次的查詢結果很可能與本次查詢結果存在交集，應將時刻ti的查詢結果納入候選集，進而由語句⑧可知CandidateKNN={B1,B2,B3,B4}.經過上述篩選過程，無需再考慮路網中所有移動對象，僅需計算CandidateKNN中的4個移動對象到A的路網距離并排序，得到時刻tj的查詢結果ResultKNN={B2,B3},如圖9(b)所示.由此可見，本文提出的推理方法可作為確定移動對象候選集的一項重要依據，能夠有效地過濾掉連續k近鄰查詢過程中的部分不合格移動對象，從而減少距離計算與排序的代價.

例1和算法OPRA4-Distance-Candidate僅給出利用本文理論模型優化連續k近鄰查詢問題的簡單示意.由于采用OPRA4模型表示方向關系，因此與QTC,QRPC中采用的十字方向關系模相比，本文提出的理論模型對空間方向信息的描述粒度更精細、基于方向關系對定性距離變化的推理粒度更精細，更有助于處理復雜交通網絡中的問題.然而在實際應用中通常還需要綜合考慮時間、速度、查詢對象的范圍、路網拓撲結構、交通規則約束等多方面因素對移動對象進行篩選，進而得到規模更小、更準確的候選集合.

4 結論與展望

面向移動空間對象，針對OPRA4方向關系與定性距離變化的結合推理問題，本文首先通過定義射線與圓之間的Rpos關系描述目標對象相對于參照對象的移動方向；然后通過組合方式定義了Rpos-pair關系，用以描述2個移動對象間的相對Rpos關系；分別研究并證明了基本Rpos-pair關系對定性距離變化的約束作用、基本Rpos-pair關系與OPRA4方向關系之間的對應關系，進而借助于基本Rpos-pair關系建立起OPRA4方向關系與定性距離變化之間的內在聯系.在此基礎上提出一種基于基本OPRA4方向關系推理定性距離變化的方法，并證明了方法的正確性.最后以智能交通中的“連續k近鄰查詢”問題為例，進一步說明了本文理論模型的正確性與有效性.

速度是移動對象的一種固有屬性，對各種空間關系(尤其是距離關系)有著重要的約束作用.如何在現有模型的基礎上進一步結合速度等時空屬性，是本文有待于深入研究的一個方面.概念鄰域能夠處理空間關系的連續變化問題，是進行時空推理的重要工具.然而基于OPRA4方向關系的概念鄰域研究較少，這方面工作將有助于深化OPRA4方向關系與其他空間關系的結合推理研究，更加全面準確地對時空信息進行表示與推理.