小子樣下導電滑環磨損失效仿真的可靠性評估研究

孫遠航，余建波，劉賢軍，孫習武，王永松

(1. 同濟大學機械與能源學院， 上海 201800； 2. 上海航天設備制造總廠， 上海 201100)

0 引 言

導電滑環作為衛星太陽電池陣驅動機構(SADA)的核心航天機電部件，其主要作用為在相對旋轉的太陽帆板和星體間傳輸電功率與信號，是整星少數幾個單點失效環節之一，其失效機理復雜，且要求其具有高可靠性、長壽命、高穩定性[1]。而導電滑環由于磨損常導致信號傳輸的不穩定甚至無法傳輸信號，使整個航天任務失敗。導電滑環由其觸頭與匯流盤形成摩擦副，再通過摩擦副傳遞電流與信號，通過接觸載荷保證觸頭與匯流盤穩定接觸，傳輸過程中伴隨有熱量產生。導電滑環摩擦副在多場耦合影響下磨損加劇，隨著磨損量的增加，滑環傳輸性能逐漸變差。

導電滑環性能試驗過程復雜且耗時長，使得獲得導電滑環的失效樣本數據困難，以往基于大樣本數據的評估方法不再適用。因此，建立導電滑環的磨損失效物理模型，是獲得滑環磨損數據的有效方法，但物理模型獲得數據往往具有小子樣特點，進而難以進行大樣本的可靠性分析。

目前可靠性分析領域中涉及機構部件的載流摩擦研究出現很多方法，其中吳杰等[2]采用試驗方法對載流摩擦在不同載荷、速度、電流下的磨損研究，但需要進行大量試驗且耗時長，且并未考慮機構的可靠性問題。任志玲等[3]基于弓網試驗數據，應用量子遺傳算法優化支持向量機的相關參數，建立受電弓滑板磨損率的預測模型，但試驗數據獲得周期較長，且該方法未考慮磨損過程的隨機性問題。尹念等[4]應用分子動力學模擬滑環摩擦副的磨損過程，但是沒有進一步研究滑環摩擦副的可靠性。劉強等[5-7]在基于機構磨損性能退化數據的基礎上，結合隨機閾值和小子樣的可靠性分析法，得出機構的可靠性相關結論。闞琳潔等[8]提出性能退化和通用生成函數相結合的系統多狀態可靠性分析方法，進行機構磨損的多性能參數退化下的系統可靠度分析。Ramalho等[9]應用磨損數據建立性能退化的可靠性評估，得出可靠性相關推論。Nicolai和Whitmore等[10-11]利用Wiener過程方法構建退化軌跡模型，進行可靠性評估。但是目前針對磨損的可靠性研究都是基于試驗得到的大樣本數據進行分析，或通過構建退化模型對結構可靠性評估，沒有將兩者有機結合分析機構可靠性。

綜上所述，本文針對滑環失效特點構建多物理場耦合的導電滑環磨損失效模型，同時考慮導電滑環測量和裝配隨機誤差，應用模型產生導電滑環小子樣退化數據，結合小子樣數據生成理論、隨機失效閾值法，對導電滑環進行可靠性評估。

1 導電滑環磨損失效模型

1.1 問題描述

導電滑環由多個環道構成，盤式滑環結構如圖1所示，通過滑環的各個觸頭與匯流盤各環道盤面接觸形成摩擦副，將電流、信號等數據進行傳輸。導電滑環摩擦副在導電滑環運行過程中，由于電流傳輸、摩擦、接觸載荷作用下，滑環摩擦副處在熱力電多場耦合的環境，多場之間相互耦合加劇摩擦副磨損。其中，觸頭與匯流盤相對滑動，形成磨屑，隨著磨屑量的增加，滑環信號傳輸產生短路、斷路等現象，信號傳輸穩定性變差；當磨屑量累計到一定量時，導電滑環失效，因此磨屑量可作為表征滑環性能好壞的退化特征量，本文針對導電滑環摩擦副的性能退化特征量構建導電滑環的磨損失效模型，應用導電滑環的磨損失效模型來仿真導電滑環退化失效過程。

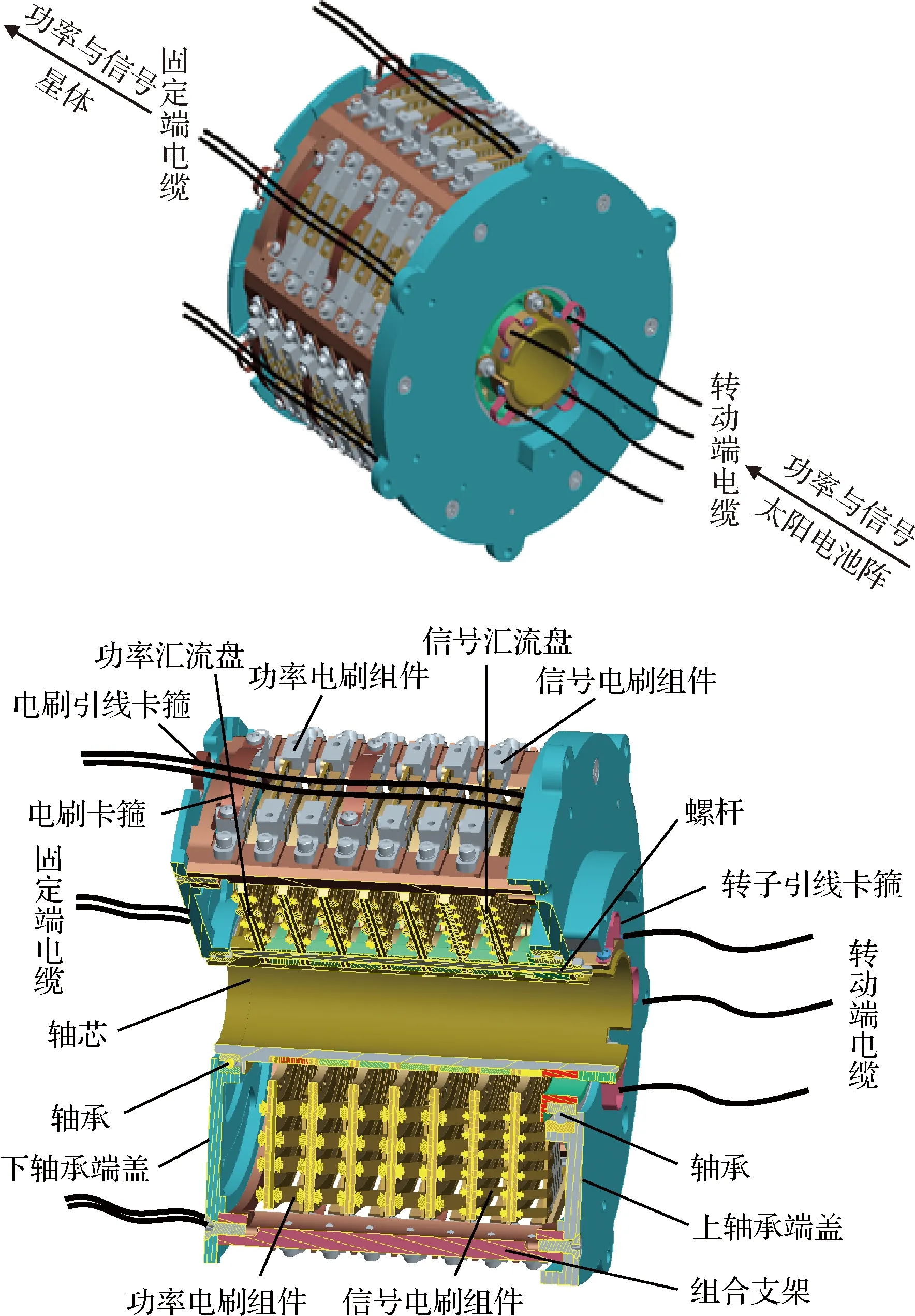
圖1 盤式滑環結構圖Fig.1 Disk slip ring structure diagram

1.2 導電滑環磨損失效模型

導電滑環摩擦副在磨損過程中，由于摩擦副熱力電多物理場之間相互耦合影響，使滑環摩擦副的磨損程度難以計算。因此，本文結合赫茲理論、傳熱學、能量守恒、Archard模型解決滑環多物理場耦合對滑環磨損影響，建立導電滑環磨損失效模型。其中應用赫茲接觸理論建立滑環摩擦副接觸模型，預測接觸載荷作用下觸頭的形狀變化，計算在接觸載荷作用下的摩擦副觸頭與盤面的接觸面積，量化接觸力對磨損影響；應用傳熱學建立摩擦副溫升模型，計算摩擦副在運行過程中的溫度變化，量化多場耦合對磨損的影響。基于Archard理論模型和本文構建的摩擦副接觸模型、摩擦副溫升模型構建滑環磨損失效模型，整個方案流程如圖2所示。

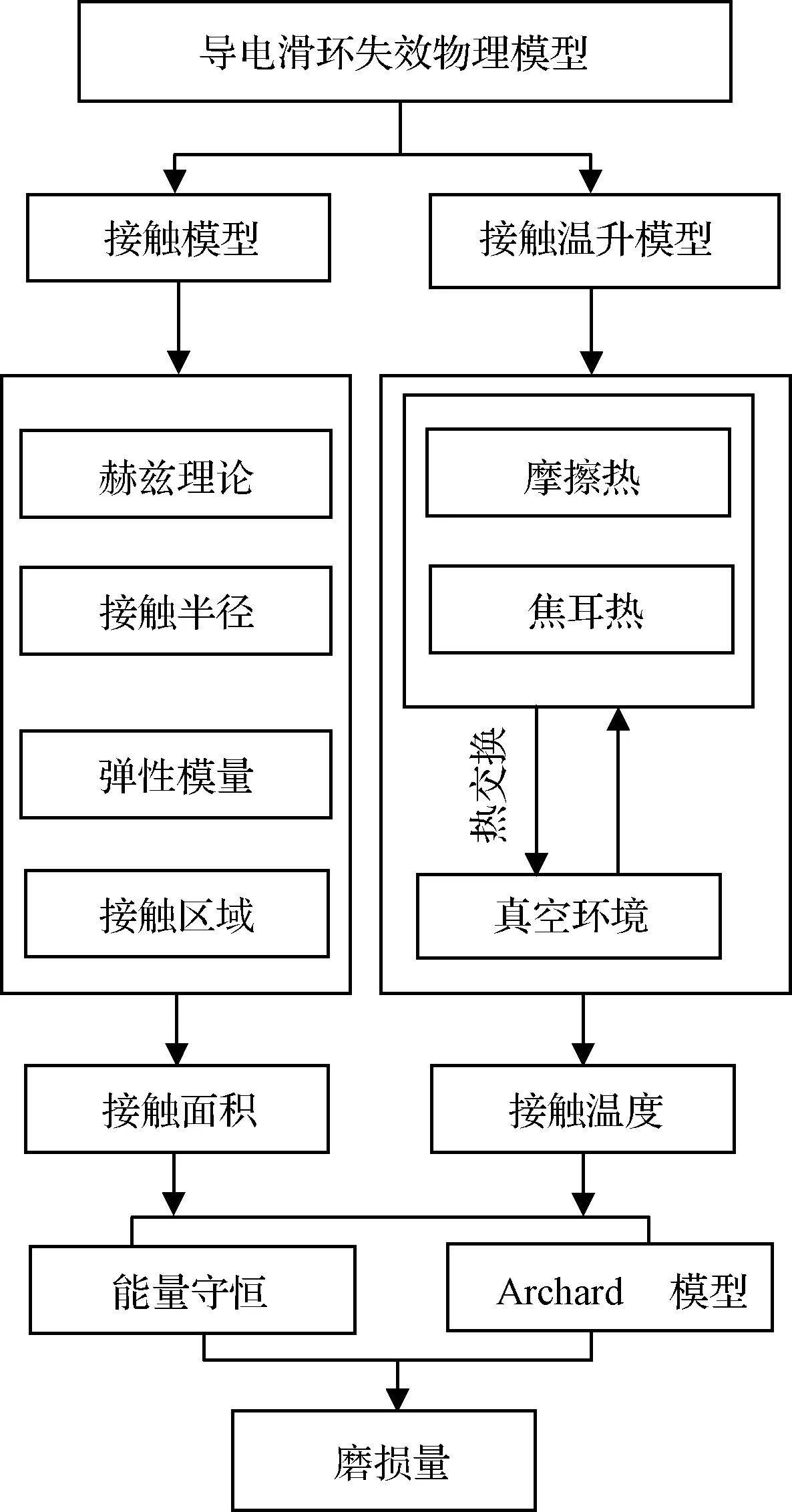
圖2 導電滑環磨損失效模型構建流程Fig.2 The process of establishing the wear failure model of conductive slip ring

1.2.1導電滑環摩擦副接觸模型

導電滑環觸頭與匯流盤在接觸載荷作用下發生點接觸，觸頭變形近似為橢球狀；隨著接觸載荷增大，接觸面積越大，接觸面積直接影響滑環摩擦副的磨損。本文通過赫茲接觸理論[12]計算摩擦副載流接觸區域面積，摩擦副簡化接觸模型如圖3所示。當觸頭與匯流盤接觸，由于材料的彈性變形，使得接觸點向鄰近四周逐漸擴展成為近似圓形區域，根據赫茲理論可得接觸區域的半徑為：

(1)

式中：F為摩擦副之間的法向接觸載荷，r和E分別為當量曲率半徑和當量彈性模量，則摩擦副觸頭與匯流盤接觸面積At為：

(2)

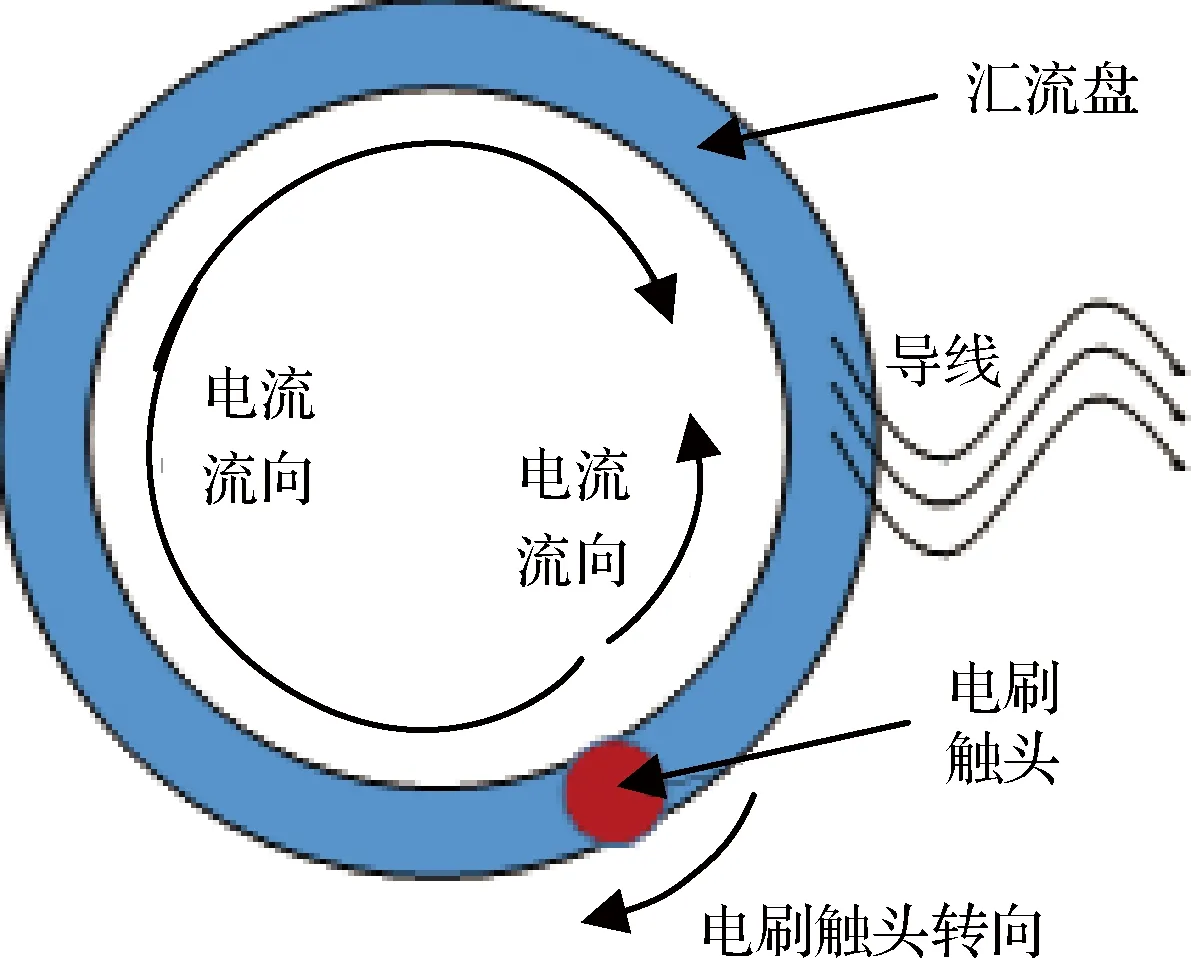
圖3 導電滑環電流傳輸Fig.3 Conductive slip ring current transfer

1.2.2滑環摩擦副接觸溫升模型

導電滑環摩擦副在運行過程中，由于熱力電多場耦合影響，產生熱量，接觸區域溫度升高，同時由于接觸區域溫度高于周圍環境，與周圍環境進行熱交換。導電滑環摩擦副熱源主要是由電流傳輸、觸頭與匯流盤鍍層摩擦產生，其中電流傳輸產生熱量包括觸頭與匯流盤之間的接觸電阻熱、電流流經盤面產生的焦耳熱。同時，導電滑環匯流盤面與周圍環境進行熱傳遞，因為導電滑環工作環境為真空，則熱傳遞方式為熱輻射。隨著盤面溫度升高，熱輻射強度越大，當產熱率與散熱率相同時，導電滑環摩擦副溫度趨于穩定，滑環摩擦副傳熱過程如圖4所示。

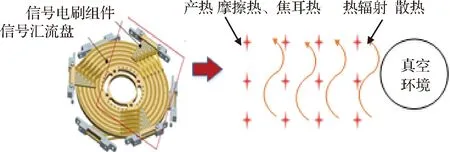
圖4 導電滑環摩擦副傳熱過程Fig.4 Heat transfer process of conductive slip ring friction pair

針對滑環摩擦副電流產熱分析，電流傳輸產生的熱量由兩部分組成，一部分為觸頭與匯流盤之間的接觸電阻和工作電流流經匯流盤產生的焦耳熱，另一部分為觸頭與匯流盤摩擦產生的熱量。針對接觸電阻產熱可直接進行計算：

P1=I2R

(3)

式中：R為觸頭與匯流盤之間接觸電阻，I為導電滑環工作電流；而對于電流流經匯流盤產生的焦耳熱而言，電流經過觸頭分兩條之路流經匯流盤，最后經過導線傳輸到星體，滑環電流傳輸過程如圖3所示，電流流經過程中，兩支路的電阻值R1，R2隨著觸頭運動處于動態變化，兩支路并聯之后電阻值為R3，則三者之間關系通過下式表示：

(4)

式中：R1與R2分別為電流流經盤面時的左側與右側盤道電阻值，兩者隨著觸頭位置變化而變化，R3為兩者之間并聯之后阻值；θ與r分別表示為觸頭對應轉過角度和圓盤半徑，ρ為盤面鍍層材料電阻率。

當轉速為nr/s時，則滑環摩擦副運轉產生的焦耳熱功率可表示為：

(5)

其中，摩擦熱是由觸頭與匯流盤滑動摩擦產生，通過摩擦力做功方法直接計算：

P3=f·F·v

(6)

式中：v為滑環觸頭轉速，f為觸頭與匯流盤之間摩擦系數。

導電滑環在真空環境下運行，其散熱方式為通過熱輻射方式傳輸熱量，根據熱輻射計算公式，可得滑環接觸區域散熱功率為：

(7)

式中：C0為黑體輻射系數，C0=5.76 W/(m2·K4)，A為單個盤道面積,Tt為滑環摩擦副的溫度值。

當散熱功率與產熱功率相等時，溫度趨于穩定，用下式表示散熱與產熱功率相等時的關系：

P4=P1+P2+P3

(8a)

將式(3)、(5)-(7)代入式(8-a)可得：

(8b)

進而求得滑環運行穩態時溫度Tt為：

(8c)

由接觸穩態溫度表達式(8c)可得知滑環摩擦副接觸穩態溫度由接觸載荷、電流、滑環結構尺寸等決定。當電流、載荷、轉速、電阻率、接觸電阻增加時，滑環穩態溫度升高，磨損加劇；當滑環盤道面積增加時，溫度下降，符合滑環運行規律，證明了溫升模型的合理性。穩態溫度直接影響著滑環摩擦副的材料特性，進而量化熱力電多場耦合對滑環摩擦副磨損的影響。

1.2.3基于Archard模型的滑環磨損失效模型

根據導電滑環目前研究可知導電滑環摩擦副磨損主要是黏著磨損，Archard模型[13]由于其所需參數少而廣泛應用于機構摩擦副的磨損計算，本文應用Archard模型來計算摩擦副磨損產生的磨屑量，計算公式如下：

(9)

式中：S為摩擦副觸頭滑動路程，V0為磨損過程中產生磨屑量體積；kv為黏著磨損常系數，通過經驗值給定[14]；H為材料硬度，其受溫度影響；F為摩擦副間的接觸載荷。同時定義觸頭與匯流盤之間單位面積磨損程度表征量黏著磨損因子fm和表征滑環失效極限的摩擦副黏著磨損強度，σm,fm和σm表達式如下：

(10)

式中：At為滑環觸頭與匯流盤實際接觸面積，已由1.2.1節部分求出。則滑環失效時運轉的路程可表示為：

S=tmax·w·R=N·Tc·w·R

(11)

式中：tmax為滑環運行失效的時間，N為滑環失效時運轉次數，Tc為滑環摩擦副運行一周的時間。摩擦副磨損過程中，觸頭與盤面結構在某一瞬間獲得的能量密度分別為總能量的一半。令盤面結構鍍層磨去厚度為δ1，觸頭結構磨去厚度為δ2，根據能量守恒可得到表達式：

(12)

由式(12)可得：

(13)

同時磨屑量體積和磨損接觸面積滿足下關系：

V0=δ·At

(14)

同時，當鍍層厚度，材料硬度，磨損系數一定時，粘著磨損強度為定值。滑環受到材料、粘著磨損顆粒等因素的影響，所以實際粘著磨損強度表示為：

(15)

式中：n為安全系數，大于1；λm為材料影響系數。最后聯立式(13)至(15)可得滑環摩擦副的失效方程：

F·C·kv·N

(16)

式中：C為滑環摩擦副周長，H1，H2分別代表觸頭、匯流盤硬度值。根據模型可以計算導電滑環摩擦副隨著運轉次數變化下的滑環摩擦副磨屑量，進而定量計算多物理場耦合對導電滑環磨損的影響。一般導電滑環的失效指標通常以磨屑質量作為失效閾值，則可通過式(16)計算的磨屑量體積與材料密度乘積作為參考。

2 滑環磨損可靠性評估方案

傳統可靠性評估常將失效閾值作為固定值，忽略了同一型號部件由于制造誤差、裝配誤差、周圍環境差異等對部件性能的影響，因此工程實際中的失效閾值往往具有隨機性。本文基于導電滑環磨損失效模型產生的仿真數據基礎上對導電滑環的可靠性進行研究，流程如圖5所示。具體流程如下：

1)考慮滑環制造、測量誤差等隨機因素對磨損的影響，對滑環磨損失效模型產生的仿真數據加入噪聲，以貼近滑環磨損的真實工況。

2)針對滑環失效模型生成的數據量偏小特點，進行虛擬增廣及Boot-strap擴展形成大樣本磨損數據，用于導電滑環的可靠性評估。

3)應用數據擬合方法分別擬合擴展前后隨運行次數變化的導電滑環磨屑量均值與標準差函數，基于導電滑環失效閾值的分布特性，分析擴展前、擴展后的固定閾值和隨機閾值下的可靠性分布，得出更加貼近實際的可靠性結論。

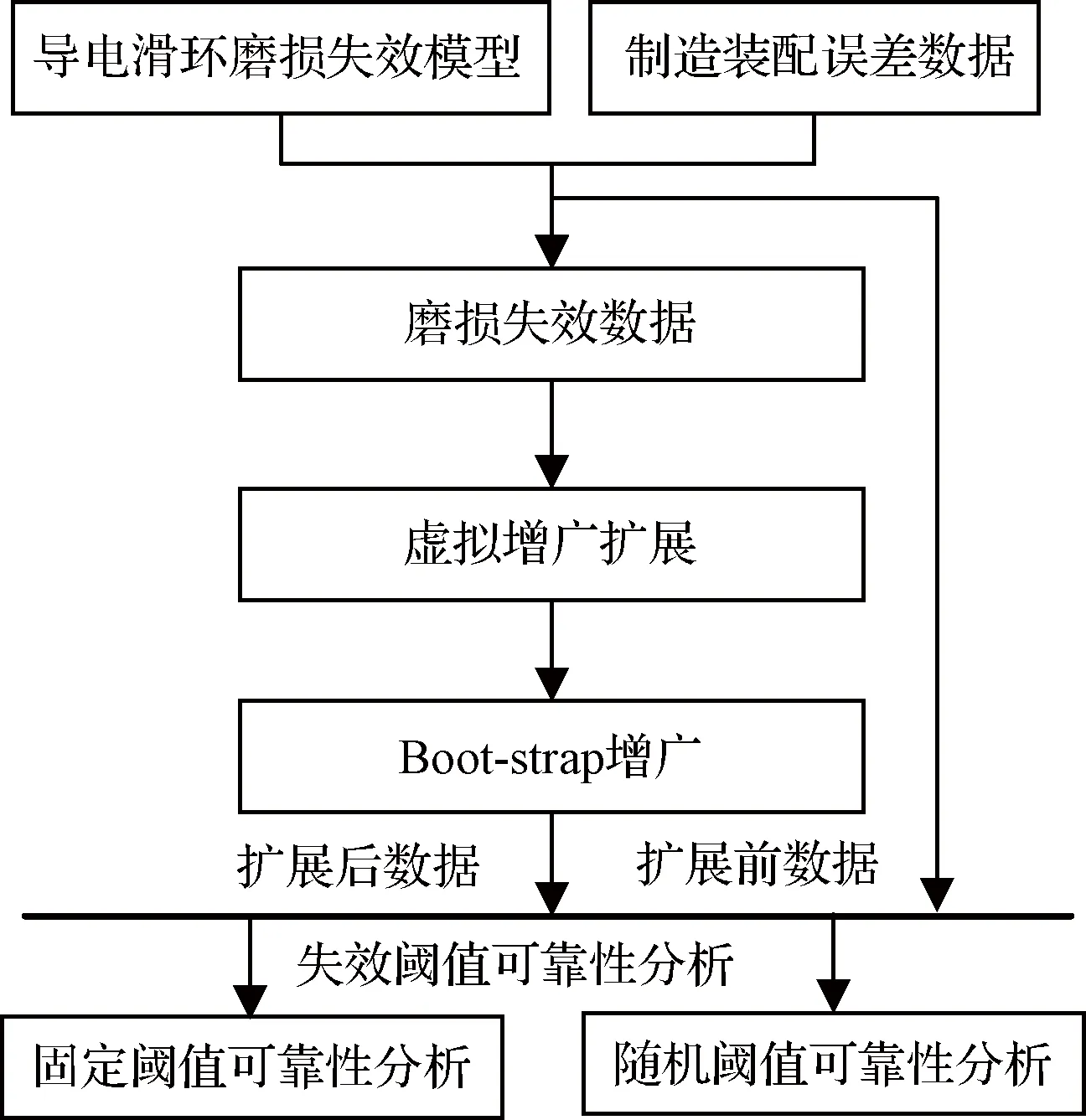
圖5 導電滑環失效閾值可靠性分析流程圖Fig.5 The flow chart of reliability analysis failure threshold of conductive slip ring

3 導電滑環磨損退化數據擴展

3.1 導電滑環失效磨損仿真數據的獲得

觸頭與匯流盤接觸的好壞決定著信號傳輸的穩定性，滑環摩擦副的接觸載荷使二者穩定接觸，本文設置接觸載荷為0.2 N，滑環的其他試驗參數按照某廠制造的滑環工藝參數設定，具體參數如表1所示。

由于測量誤差，實際接觸載荷會在測量裝置最小刻度上波動，實驗測量裝置最小刻度為0.02 N，則接觸載荷測量誤差在最小刻度范圍內波動。因此基于裝置測量誤差，實際接觸載荷在0.18～0.22 N范圍波動，本文通過計算導電滑環失效物理模型在0.18 N,0.19 N,0.2 N,0.21 N,0.22 N,等5種載荷下的磨損來近似模擬滑環在接觸載荷0.2 N下的磨損，考慮到滑環單圈的磨損變化量非常微弱，其額定壽命為60000 r，完全失效約在100000 r，所以本文以20000 r作為一個磨損周期，計算5個周期的磨損情況。同時由于導電滑環摩擦副鍍層、觸頭的制造工藝的差異性以及工作環境等隨機因素影響，在磨損數據加入高斯噪聲近似模擬制造裝配過程的隨機誤差，得到5組樣本數據如表2所示。

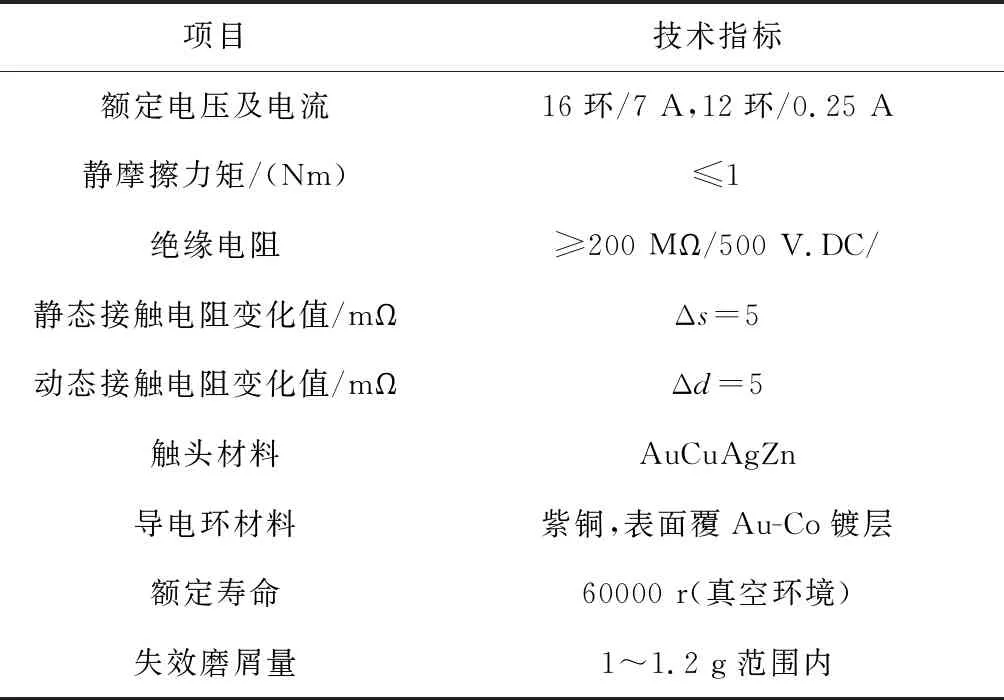
表1 導電滑環組件性能指標Table 1 Performance index of conductive slip ring component

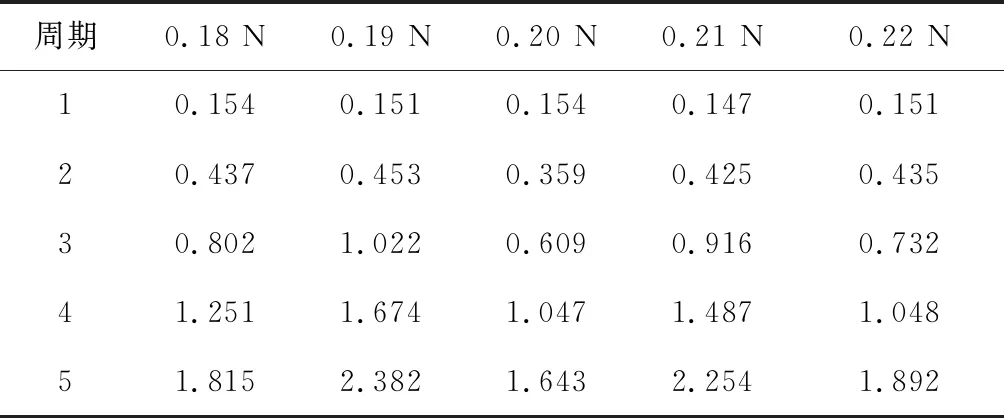
表2 不同接觸載荷下各周期磨損量Table 2 Wear amount of each cycle under different contact loads g

3.2 磨損小子樣數據擴展

根據導電滑環磨損失效模型得到了5組退化樣本數據，但數據量偏少，無法更好的用于可靠性評估，因此采用虛擬增廣法及Boot-strap法進行擴展得到大樣本數據。首先，通過虛擬增廣法[15]將表2中原始樣本數目n=5增廣到樣本量n=13的樣本數據，且每個樣本數據容量仍為5，具體增廣方法如下：

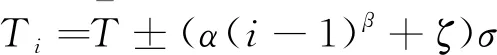
(17)

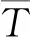
(18)

聯立式(17)、(18)結合求解出ζ,進而求解出新樣本數據，此時樣本數據量擴展為13組，再采用指數Boot-strap法進行再二次擴展，利用樣本本身的信息，對于總體分布不需要做出假設方法，結合虛擬增廣數據及Boot-strap得到21組數據樣本數據，如表3所示。

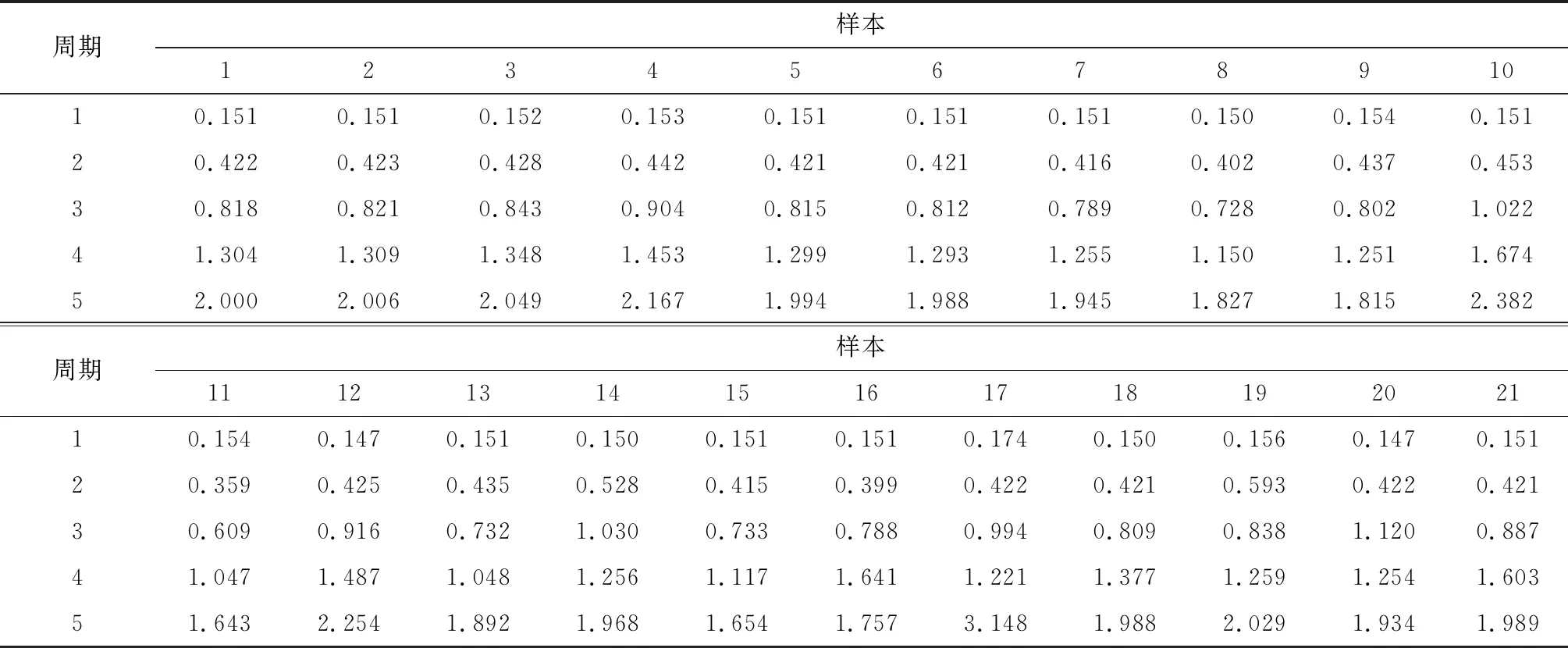
表3 指數Boot-strap擴展之后的導電滑環磨損數據樣本Table 3 Slip ring wear data samples extended index Boot-strap

4 導電滑環失效閾值可靠性評估

4.1 滑環退化分布特征量

根據導電滑環磨損失效模型產生數據表2及經過磨損數據增廣得到數據表3，進而計算導電滑環磨損量在各周期的均值和標準差，擴展前后的均值與標準差變如表4與表5所示。

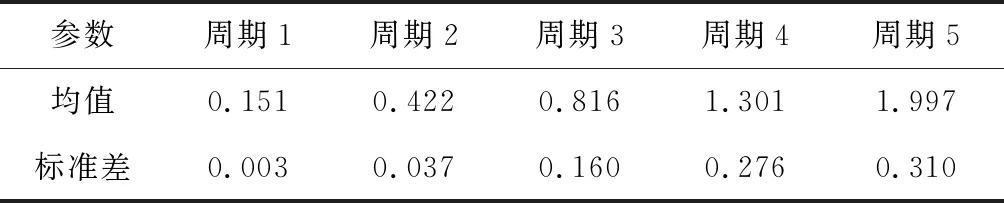
表4 擴展前各周期的樣本均值與樣本標準差Table 4 Sample mean and sample standard deviation of each period before expansion

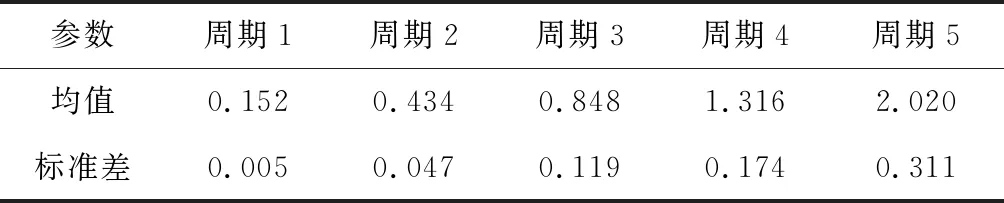
表5 擴展后各周期的樣本均值與樣本標準差Table 5 Sample mean and sample standard deviation of each period after expansion

根據表4與5數據可得擴展前后均值、標準差隨運轉周期變化的磨損量變化曲線如圖6所示，由圖6可以發現導電滑環擴展前后磨損樣本數據的標準差、均值隨著運轉次數增加呈線性變化。本文應用最小二乘法擬合擴展前后樣本數據均值和標準差隨運轉次數變化的函數為：

(19)

(20)

式中：t為導電滑環的運行次數，μ(t),σ(t)分別為磨損樣本數據擴展后均值、標準差隨運轉次數變化的函數，μ0(t)與σ0(t)為磨損樣本數據擴展前均值、標準差隨運轉次數的變化函數。

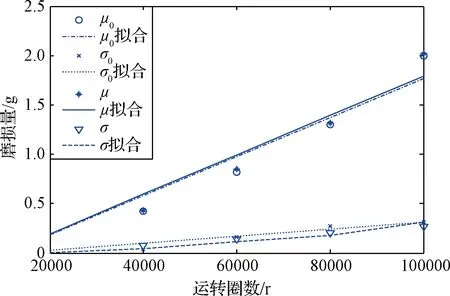
圖6 擴展前后樣本數據的均值標準差隨運轉次數變化曲線Fig.6 Variation and mean variance curve of wear sample data with operation times before and after expansion

磨損機構單位周期磨損量往往呈現正態分布規律[16],對導電滑環的磨損量仿真數據進行正態分布K-S檢驗，結果顯示滑環磨損量在5種載荷磨損量下均服從正態分布規律，因此本文設定滑環在磨損過程的磨屑量呈現正態分布規律。

4.2 導電滑環固定閾值下的可靠性評估

傳統的航天部件可靠評估分析中，常以失效閾值作為固定值。本文以某廠制造的導電滑環為例，其磨損經驗失效閾值在1～1.2 g范圍內波動，磨損量服從正態分布，固定閾值下的失效分布函數為：

(21)

進而可計算固定閾值可靠度函數R(t)為：

(22)

式中：t為導電滑環的運轉次數，W為導電滑環運動過程中的磨損量，Wf為導電滑環磨損量的失效閾值，μW(t),σW(t)分別為磨損過程中均值、標準差隨運轉次數變化的函數，將式(19)、(20)代入式(22)可得滑環磨損數據擴展前后固定閾值下的滑環可靠度函數，分別計算固定閾值1 g、1.2 g下滑環可靠性分布函數，結果如圖7所示。一般將可靠度等于90%時的壽命為產品的額定壽命，由圖7中發現，擴展后的高可靠度階段曲線比擴展前的曲線變化較平緩，較貼近生產實際；在可靠度較低階段時，擴展后數據的可靠度變化曲線比擴展前數據變化快，也符合工程實際情況。

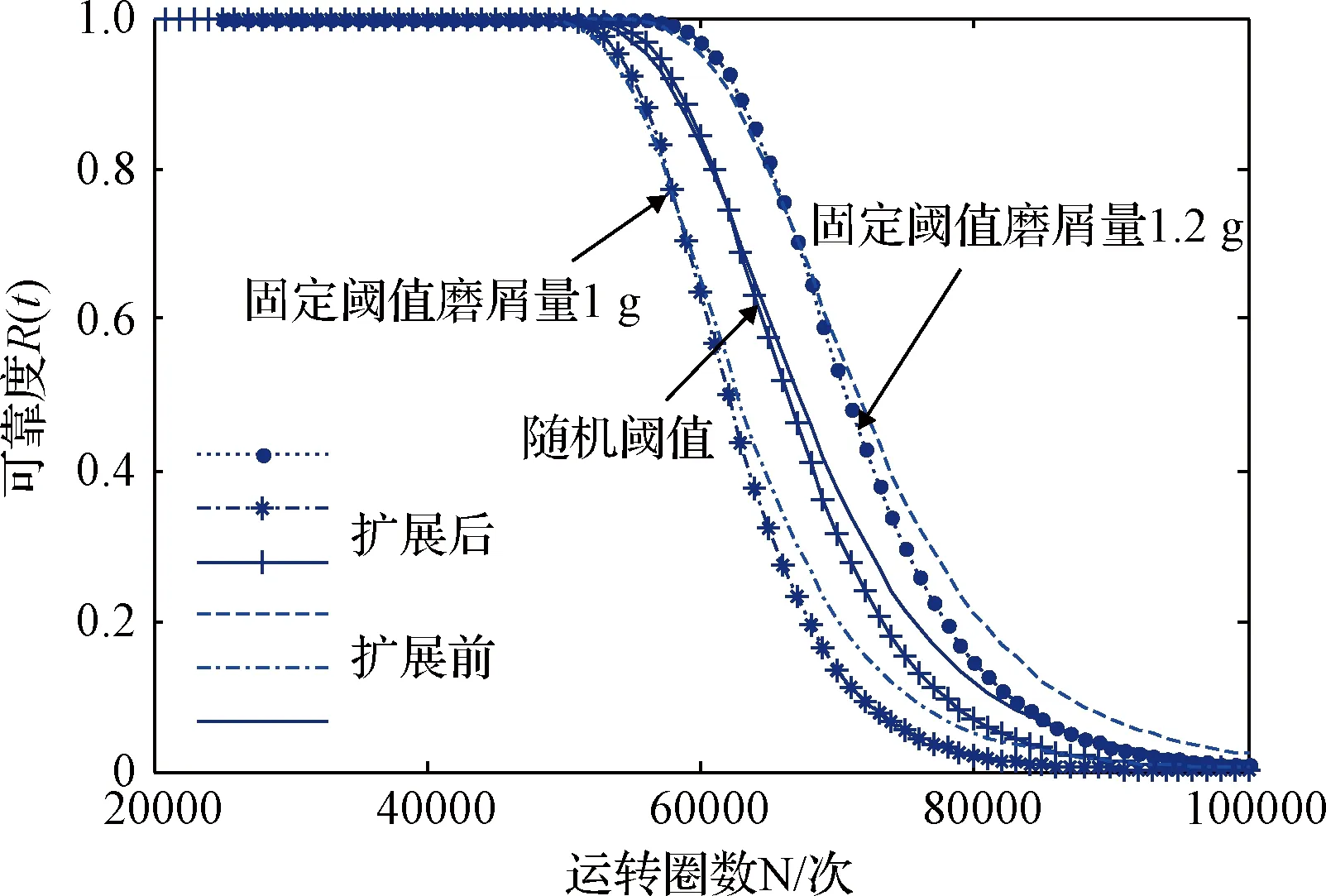
圖7 導電滑環擴展前后磨損樣本數據的可靠性分布Fig.7 Reliability distribution of wear sample data before and after expansion of conductive slip ring

4.3 導電滑環隨機閾值下的可靠性評估

以往航天部件的失效可靠性評估分析，經常將閾值作為固定值進行分析，但是實際工程中由于環境、制造的差異原因，閾值并非為固定數值，因此將失效閾值設定為隨機值更加符合工程實際，本文假設滑環失效閾值在1～1.2 g區間均勻分布且滑環磨損量服從正態分布，則滑環的失效概率密度函數和磨損量概率密度函數為：

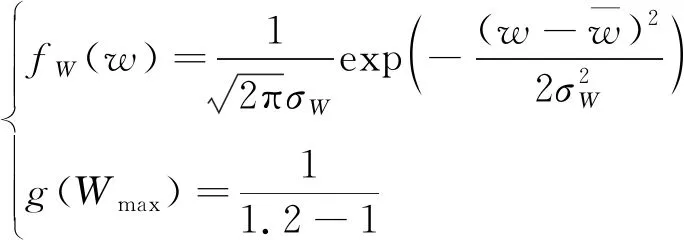
(23)

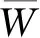
(24)

式中：R(t)與F(t)分別為滑環的可靠度函數和失效分布函數，μW(t)與σW(t)分別為滑環磨損量均值與標準差隨運轉次數變化的函數。將擴展前后均值、標準差函數代入可靠性函數中，得到隨機可靠性曲線如圖7所示。從圖7中可以看出擴展后隨機閾值在可靠度90%以上的持續時間高于擴展前數據可靠度，且在高可靠度階段曲線變化平緩；在低可靠度階段，曲線變化快，與實際工況更符合。證明本文提出的擴展數據方法具有合理性和可靠性。因此本文以擴展后數據對導電滑環進行可靠性評估分析，得到導電滑環可靠度函數如圖8所示。

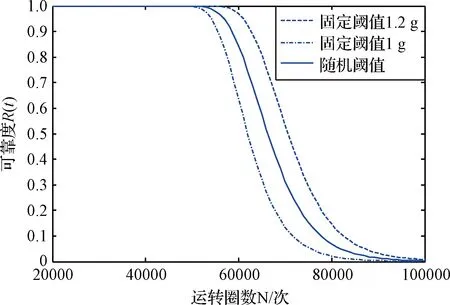
圖8 基于擴展后數據在不同閾值下的滑環可靠性分布Fig.8 Reliability distribution of slip ring based on different thresholds of extended data

從圖8中可以得到導電滑環部件不同閾值下的額定壽命分別為：53000次、58000次、63000次，本次試驗的隨機閾值額定壽命更加貼近實際，且在可靠度在90%之后變化幅度相比固定閾值平緩，隨機閾值避免了以固定閾值作為失效極限造成的主觀誤差，更加貼近導電滑環的實際磨損情況。

5 結 論

1) 由于導電滑環真實磨損試驗成本高、周期長的特點，建立基于多場耦合的滑環磨損失效模型。針對滑環摩擦副在多物理場耦合的特點，應用赫茲接觸理論、傳熱學、能量守恒量化熱力電多場耦合對磨損影響，結合Archard模型構建滑環磨損模型。基于磨損模型對滑環磨損過程進行仿真，得到滑環磨損仿真數據，為機構系統性能退化和可靠性研究提供數據。

2) 結合小子樣的虛擬增廣法、Boot-strap法對滑環磨損仿真試驗數據進行擴展，并基于退化量分布特點得到擴展前后磨損量均值和標準差隨導電滑環運行次數變化的函數。

3) 用擴展前后的磨損數據對滑環機構可靠度進行評估，得到固定閾值、隨機閾值下的可靠度曲線對比圖。擴展前后數據的可靠性曲線相似，且擴展后數據變化更加符合生產實際，證明數據增廣方法的可靠性。同時為避免固定閾值可靠性評估分析的主觀誤差，應用隨機閾值進行滑環的可靠性評估，結果表明基于隨機失效閾值下滑環可靠性評估比固定閾值下可靠性評估預測的失效過程更符合生產實際。因此本文的方法填補導電滑環因缺少數據而難以進行可靠性研究的空白。