某裝備車門橡膠密封條密封性敏度分析及改良設計

王曉輝, 常 亮, 聶小華, 鮑志光

(1.中國飛機強度研究所，西安 710065; 2.內蒙古第一機械集團有限公司，包頭 014032)

隨著車輛裝備工業的發展，人們對車輛裝備的要求已經不局限于舒適性、防振性、隔噪等基本性能要求，尤其是在深水、高原、極地等特殊復雜的惡劣環境中，對于車輛裝備的安全性、密封性及可操作性的要求更高，并具有重要的現實意義。為了提高產品的設計質量和效率，在密封條產品設計過程中要重點關注其功能性和可靠性。中外學者對此展開了一系列研究。Luo等[1]首次使用高次的材料模型來仿真模擬大變形行為，但無法確保應力模擬分析的正確性。Dikmen等[2]借助試驗數據分析了各種橡膠材料模型擬合密封條力學性能的可靠程度，考察了整車動態性能受其影響程度。黃艷敏[3]仿真模擬了轎車車口密封截面的插拔變形與彎曲變形過程，并給出改善方法。趙建才等[4]針對轎車車門密封條的壓縮變形進行了計算仿真分析和優化設計，為密封條設計提供了有價值的信息。陳少偉[5]采用智能算法思想開拓了一種求解密封條本構模型系數的自動化方法。王勇[6]建立了密封條的幾何模型與橡膠材料模型，并確立了有限元分析的邊界條件，實現對轎車車口密封條結構參數的優化設計。從國內外研究趨勢和現狀綜合來看，目前對于橡膠材料本構模型的研究和橡膠壓縮變形性能的數值模擬依然是密封性研究領域的熱點問題之一。針對密封條結構優化設計的研究在最近幾年才開始起步，大多是針對密封條結構的主要參數(如截面形狀和壁厚)進行獨立優化[6-8]，沒有綜合考慮結構參數的影響，缺少具體的改良構型設計方案，因此該方面的技術研究目前尚屬空白。

計算機輔助設計(computer aided design，CAD)和計算機輔助工程(computer aided engineering，CAE)技術作為當前最為先進科學的設計分析方法，廣泛應用于各個行業，充分發揮了“多、快、好、省”的特點。為此，對某型車輛裝備駕駛門密封條進行了有限元求解分析，通過綜合密封條結構截面參數的敏度分析，實現了密封條幾何構型改良設計，獲得良好分析結果，為產品設計過程提供重要參考依據。

1 車門密封條有限元建模

車門作為常規結構其建模方法較為簡單，為了節省篇幅，這里只簡單介紹密封條的建模方法。

1.1 車門密封條結構特點

簡化后的駕駛室車門模型如圖1所示。

1為玻璃窗框；2為門板；3為車門合頁組件；4為門把手與鎖子系統；5為門框側圍；6為車門雨檔；7為加強筋板01；8為加強筋板02；9為門框；10為橡膠密封圈；11為其他附件。圖1 簡化后的車門模型Fig.1 Simplified rear door model

駕駛門密封條主要由3部分組成，幾何結構如圖2所示。其中硬橡膠硫化在金屬骨架上，用于固定在車體上；結構鋼在U形件中起到加持作用；軟橡膠位于密封條最外側的部分，主要承受車門關閉時的壓縮載荷，以產生密封性和回彈性，同時可彌補車門與車體之間間隙的不均勻性。

圖2 車門密封條幾何結構Fig.2 Geometrical structure of weatherstrip seal for car door

1.2 材料本構模型的建立

對于密封條橡膠材料，在大變形情況下通常作為超彈性材料處理，因此可使用基于應變能密度函數的本構模型來描述。分析模擬中，結構鋼采用常用的金屬材料屬性，由于橡膠屬于高度非線性材料，考慮到材料本構模型的多樣性和硬橡膠與軟橡膠的材料本構關系，在參考文獻和工程經驗的基礎上[9-11]，選擇Mooney-Rivlin模型(50%～150%應變范圍內的變形)中兩參數模型，可得到比較高的精度，計算過程如下。

假設體積均為不可壓縮，利用簡化后的僅有2個材料常數的應變能函數，即

W=C10(I1-3)+C20(I2-3)

(1)

式(1)中：C10、C20為材料常數；I1、I2為第一、第二不變量；W為應變能，物理單位均為1。通過單軸拉伸試驗分別得到軟橡膠(LH-25B)單軸拉伸試驗曲線(圖3)和硬橡膠(LH-75B)單軸拉伸試驗曲線(圖4)。進一步通過經驗公式可得橡膠材料的本構系數。

已知兩種橡膠類型分別為LH-25B和LH-75B發泡橡膠，試驗采用啞鈴片狀試樣，其尺寸參數如表1所示。

圖3 LH-25B型橡膠單軸拉伸試驗Fig.3 Uniaxial tensile test for LH-25B rubber

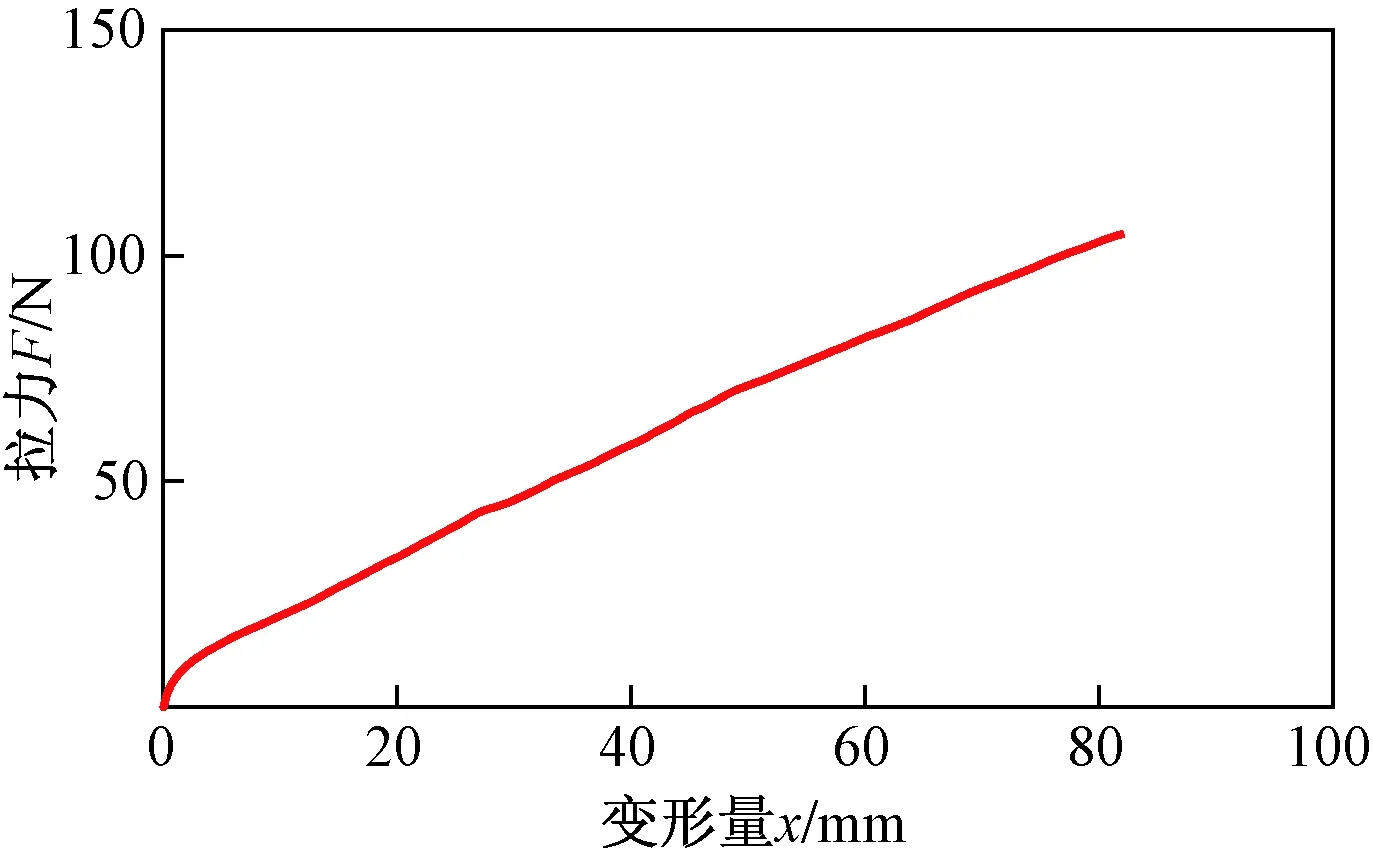
圖4 LH-75B型橡膠單軸拉伸試驗Fig.4 Uniaxial tensile test for LH-75B rubber

表1 兩種橡膠試驗件的尺寸參數

分別取兩種橡膠拉伸試驗中F-x曲線(圖3和圖4)上一點，其中LH-25B取點(70 mm，60 N)，LH-75B取點(40 mm，60N)。根據應力計算公式σ=F/A可得截面上的應力分別為4.63 MPa和4.42 MPa。再根據應變計算公式ε=x/l可得應變量分別為2.8和1.6。最后根據彈性模量計算公式E=σ/ε可分別得E為1.65 MPa和2.76 MPa。由經驗公式(2)計算得到兩種橡膠的材料常數分別如表2和表3所示。

E=6(C10+C01)，C10≈4C01

(2)

式(2)中：C10、C01為橡膠本構模型的材料常數。

表2 橡膠的材料常數

注：D0為橡膠本構模型的材料常數。

表3 結構鋼的材料屬性

1.3 車門密封條有限元模型的建立

由于車門密封條在周向上的幾何尺寸遠大于其他兩個方向，在車門關閉過程中周向變形很小，因此密封條可以簡化為平面問題。根據密封條的結構特點，對密封條進行網格劃分，分別使用了體元、殼元和梁元。對于車門密封條橡膠部分的建模，為了減小橡膠部分的計算規模，使整個非線性接觸分析能更好地收斂，考慮將整段橡膠分段處理，如圖5所示，分成彎段、直段和直段-彎段連接處3部分進行研究。圖6所示為車門密封條有限元模型。

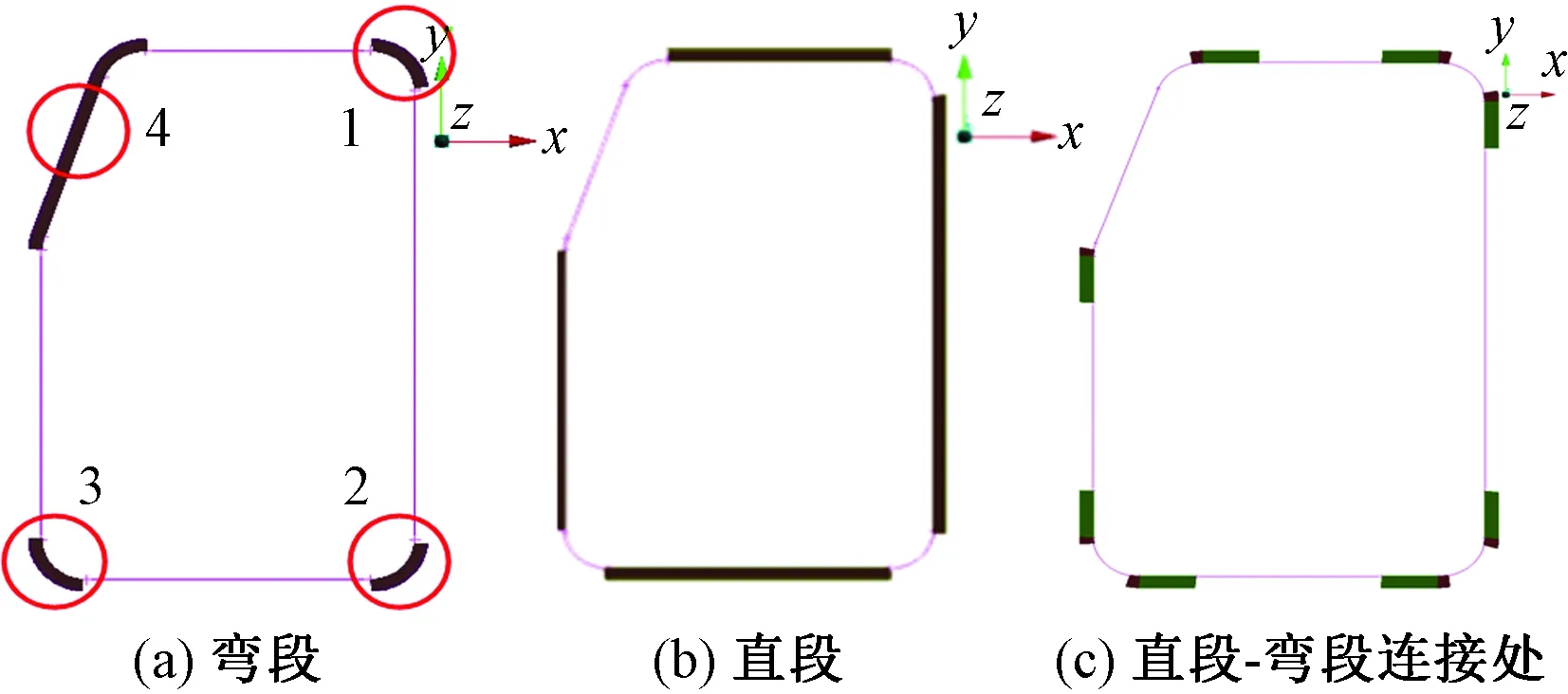
圖5 車門密封條橡膠分段處理Fig.5 Segmentation diagram of car door seal rubber

圖6 車門密封條有限元模型Fig.6 Finite element model of car door seal

考慮到密封條結構特點，車門與對于模型中存在的接觸采用面-面(surface-to-surface contact)的接觸形式進行定義。為了提高分析效率，以下只取軟橡膠截面二維分析模型，如圖7、圖8所示。為了研究軟橡膠的截面參數對密封性的影響，在此通過改變軟橡膠的壁厚、小尖的截面形狀和下部加強圓半徑的大小，來研究最大接觸壓力與上述參數的敏度大小的關系。

圖7 橡膠截面二維分析模型Fig.7 Two-dimensional analysis model of rubber section

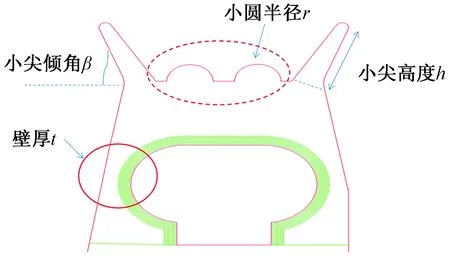
圖8 軟橡膠截面參數二維分析模型Fig.8 Two-dimensional analysis model of soft rubber section parameters

2 密封條軟橡膠截面參數敏度分析

2.1 軟橡膠壁厚變化對接觸壓力的影響

為了研究軟橡膠壁厚t的大小對密封性的影響，在保證其他參數不變的情況下，分別取壁厚t=1.1～1.9 mm進行橡膠的壓縮分析，分析結果如表4、圖9和圖10所示。

表4 不同壁厚下軟橡膠上最大接觸壓力

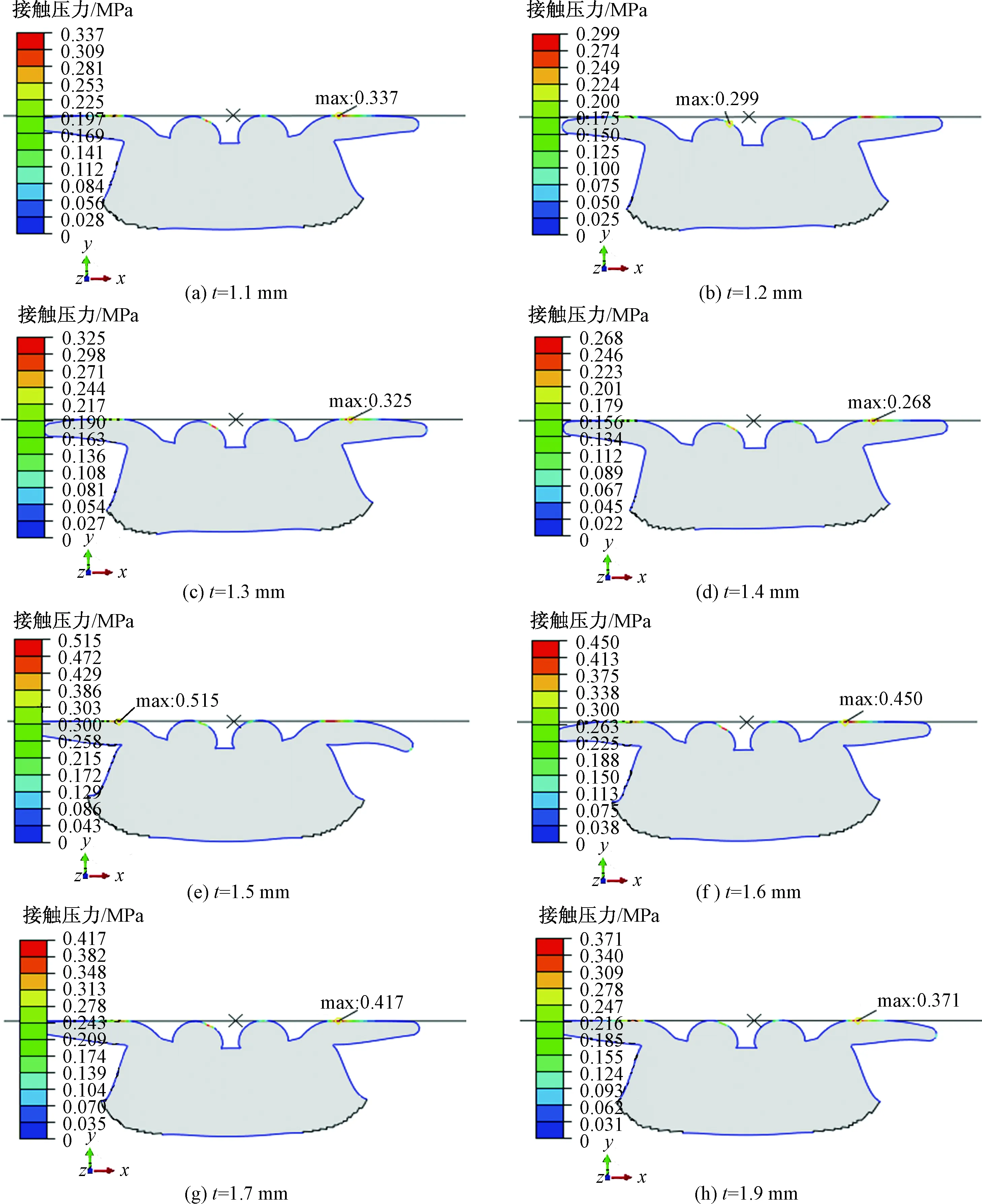
圖9 不同壁厚(t=1.1～1.9 mm)時橡膠上接觸壓力云圖Fig.9 Contact pressure cloud diagram on rubber with different wall thickness (t=1.1～1.9 mm)

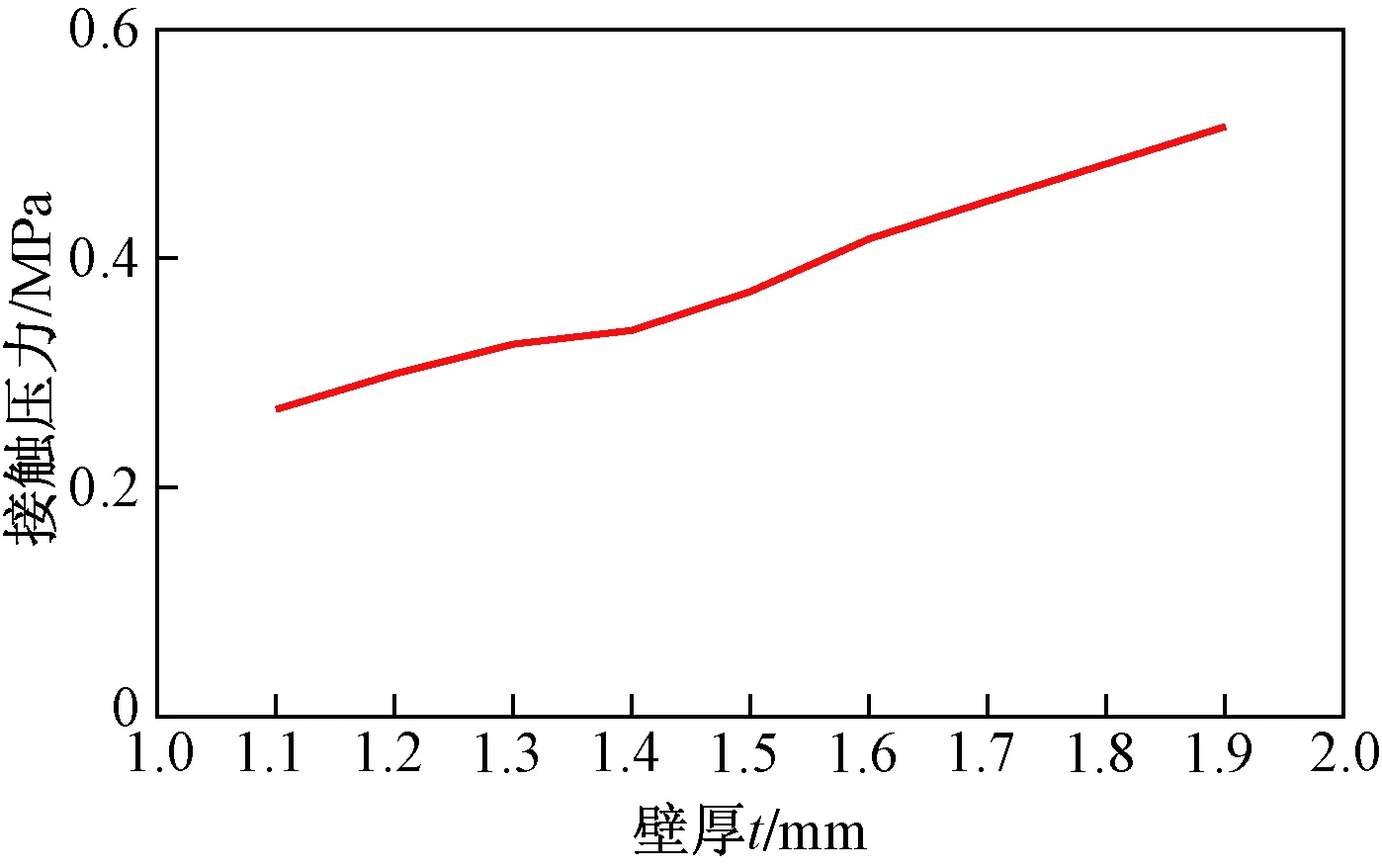
圖10 最大接觸壓力隨壁厚變化曲線Fig.10 Maximum contact pressure as a function of wall thickness

通過表4和圖10分析可知，隨著壁厚的增加，軟橡膠密封唇上的接觸壓力呈不斷增長的趨勢。在橡膠實際密封過程中，密封唇上的最大接觸壓力越大，相應的密封性也越好。因此，在設計橡膠密封圈壁厚時，應在滿足密封的情況下，考慮將壁厚設計得稍厚一些。

2.2 軟橡膠加強圓半徑變化對接觸壓力的影響

為了研究軟橡膠加強圓半徑r的大小對密封性的影響，在保證其他參數不變的情況下，取半徑r=0.8～1.5 mm進行橡膠的壓縮分析，分析結果如表5和圖11所示。

表5 不同半徑下軟橡膠上的接觸狀態

圖11 最大接觸應力隨小圓半徑變化曲線Fig.11 Maximum contact stress as a function of the radius of the small circle

通過表5和圖11分析可知，隨著半徑的減小，軟橡膠上的接觸壓力呈增長的趨勢，最大接觸壓力的位置均在右側密封唇上，靠近內側的傾角附近。進一步分析，軟橡膠上的兩個小半圓上的接觸狀態發現，隨著半徑的減小，車門與兩半圓的接觸狀態逐漸由接觸變為分離，相應在小圓處密封性降低。

2.3 軟橡膠小尖截面形狀對接觸壓力的影響

為了研究小尖截面形狀對密封性的影響，在保證其他參數不變的情況下，如圖8所示，選擇小尖的高度h及傾角β作為研究對象進行分析。

2.3.1 小尖高度對密封性的影響

分析結果如表6和圖12所示。通過表6和圖12分析可知，小尖高度的變化對軟橡膠上的接觸壓力影響較小。

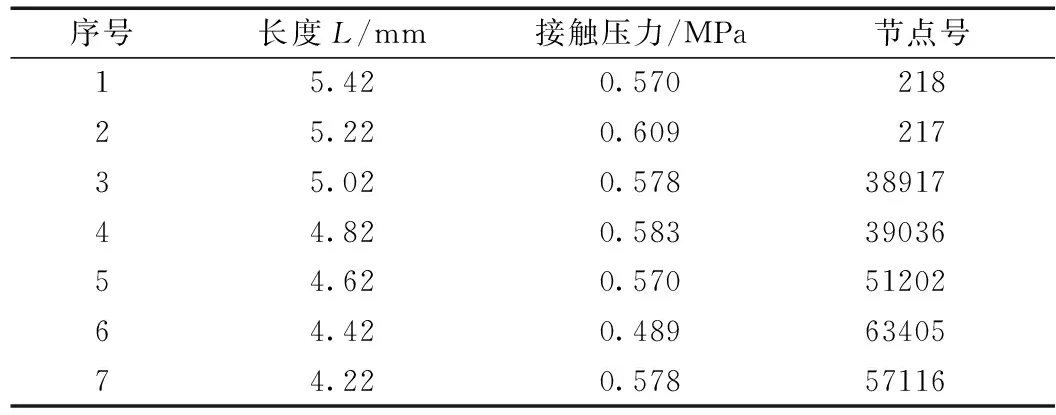
表6 不同小尖高度軟橡膠上的接觸壓力

圖12 最大接觸壓力隨不同高度的變化曲線Fig.12 Maximum contact pressure as a function of height

2.3.2 小尖的傾角對密封性的影響

分析結果如表7和圖13所示。通過表7和圖13分析可知，小尖傾角的變化對接觸壓力的影響相對較小。

表7 不同小尖傾角下軟橡膠上的接觸壓力

圖13 最大接觸壓力隨小尖傾角的變化曲線Fig.13 Curve of maximum contact pressure as a function of small tip angle

3 密封條軟橡膠截面構型改良設計

為了在保證密封性的前提下，盡量減小橡膠的質量，需要根據上述敏度分析的結果對當前構型進行改良，并對比改良前后橡膠在質量和密封性等方面的差異。

3.1 構造新的幾何構型

為了減少研究對象的規模，重點研究敏度較大的因素對密封性的影響。因此，基于以上分析結果，選取軟橡膠壁厚t和加強圓半徑r作為研究對象來構造新的幾何構型。

根據二維計算的結果可知，當小圓半徑r減小到1.3 mm時，車門與小圓開始出現分離現象，當小圓半徑減小到1.1 mm時，車門與兩小圓完全分離，從而使橡膠的密封性降低。因此，初步將小圓半徑減為1.3 mm(即減小13.3%)和1.1 mm(即減小26.7%)。對于壁厚t的選擇，由于接觸壓力隨壁厚減小呈遞減的趨勢，且不確定工作壓力的大小，因此很難確定接觸壓力的臨界值，從而也就無法選擇對應的壁厚大小。故初選壁厚為1.7 mm(即減小10%)和1.5 mm(即減小21%)。經過小圓半徑r的取值與壁厚t的取值組合，共確定2×2=4種改良構型，具體如表8所示。

表8 4種典型改良構型設計方案

3.2 有限元計算結果與對比分析

為了驗證改良后橡膠的密封性，需要對新構型進行三維實體模型的壓縮分析。為此，選取圖5中的直段樣條進行三維仿真計算。鑒于篇幅原因，在此給出整體模型和直段1橡膠在5種構型下的分析結果，如圖14～圖18所示。

圖14 原始構型分析結果Fig.14 The analysis results of the original configuration

同理，將標號為1～8的各直段橡膠上接觸壓力進行對比分析，結果如表9和圖19所示。

此外，取直段1上的軟橡膠作為樣條橡膠，以質量為目標進行了優化計算，結果如表10所示。

通過表9、表10和圖14分析可知：

(1)構型1上每段橡膠的接觸壓力變化曲線與原始模型吻合度較高，表明構型1在保證與原始模型相同的密封性前提下，達到了減重的目的。

圖15 改良構型1分析結果Fig.15 The analysis results of the configuration 1

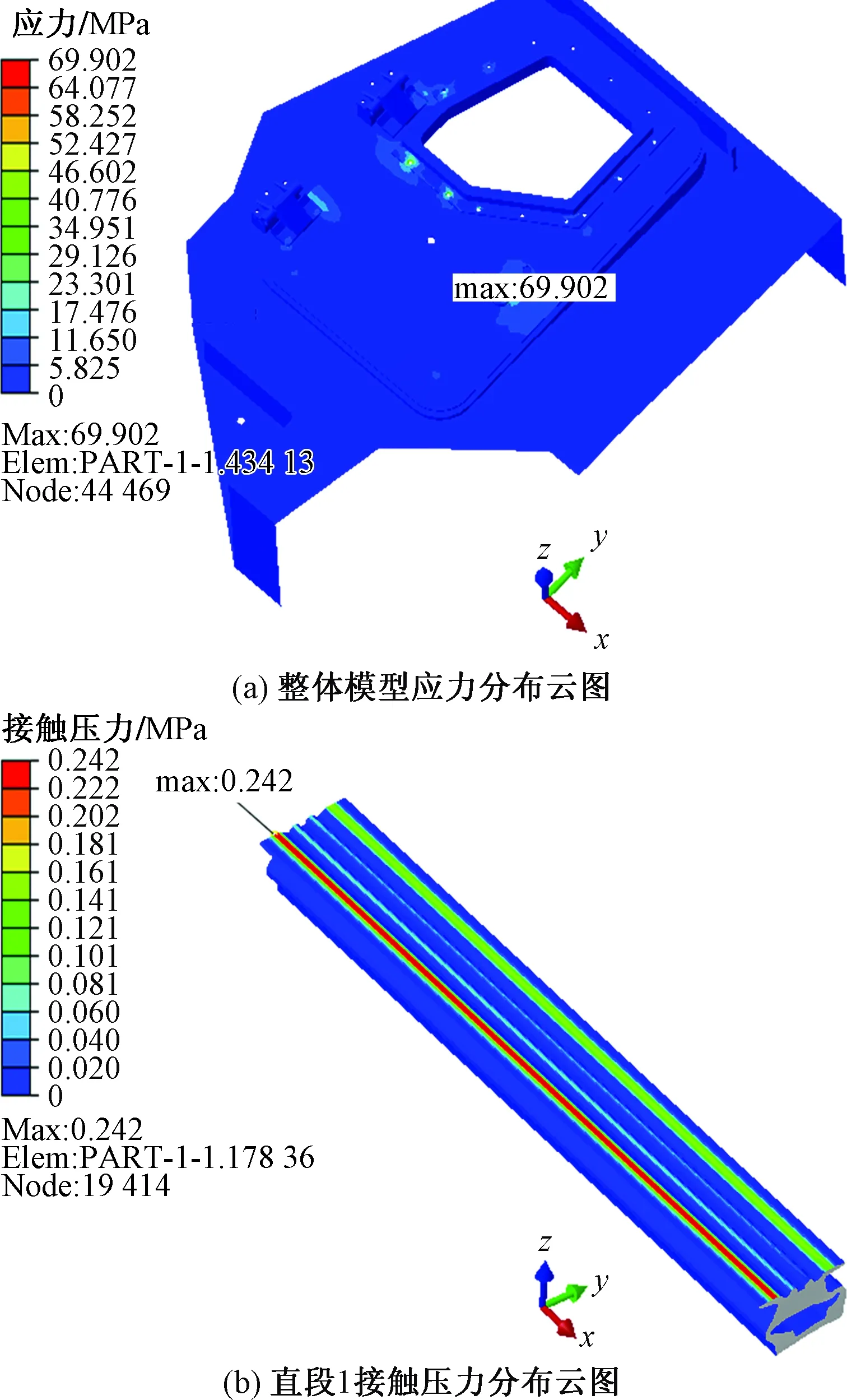
圖16 改良構型2分析結果Fig.16 The analysis results of the configuration 2

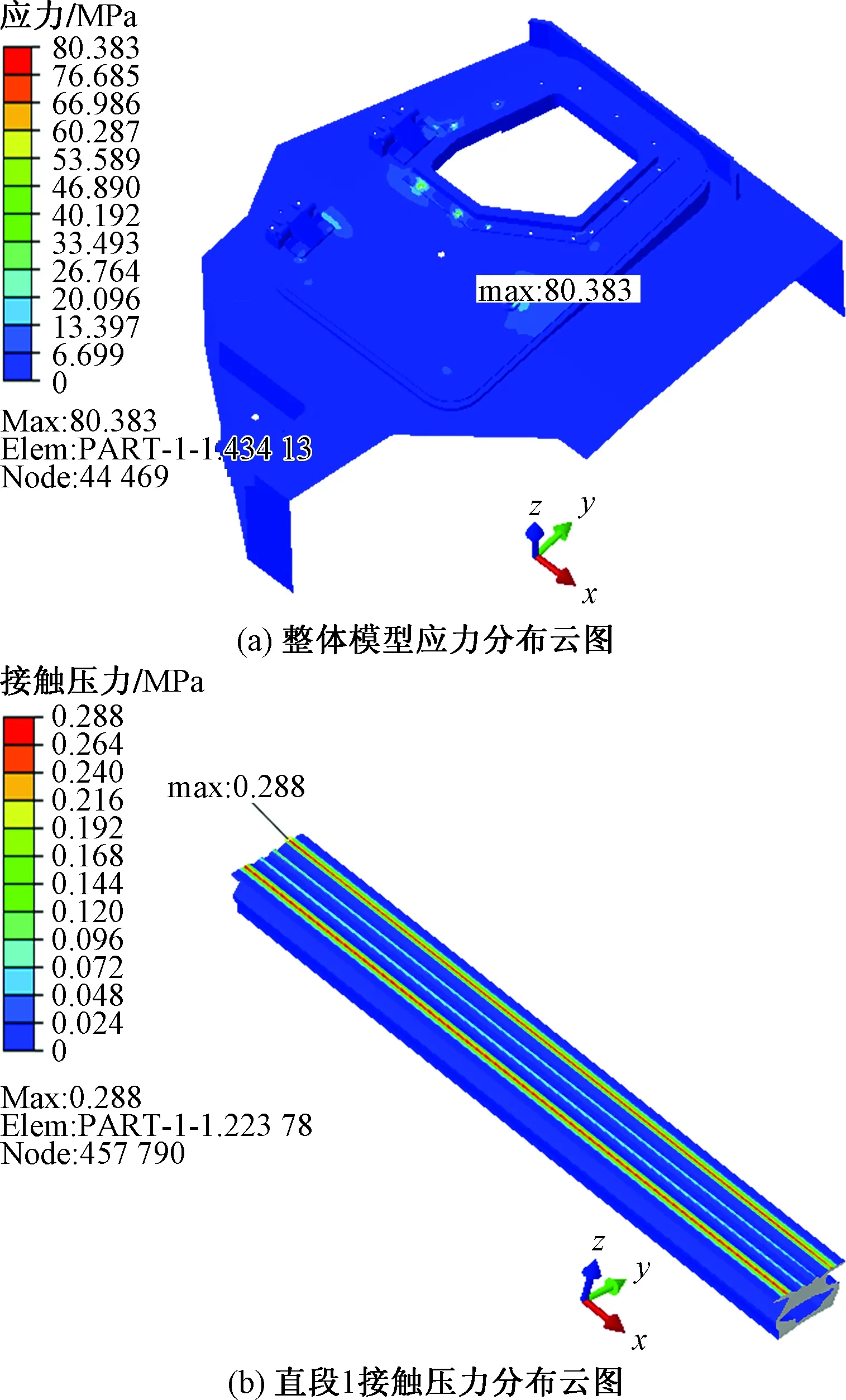
圖17 改良構型3分析結果Fig.17 The analysis results of the configuration 3

圖18 改良構型4分析結果Fig.18 The analysis results of the configuration 4

表9 5種構型下直段橡膠的最大接觸壓力

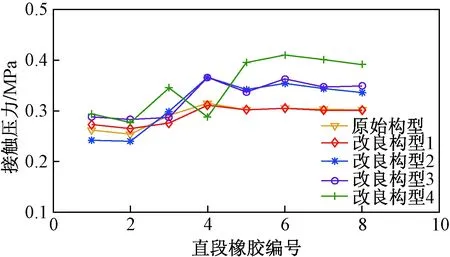
圖19 5種構型下直段橡膠上的接觸壓力變化曲線Fig.19 Curve of contact pressure on straight rubber under five configurations

表10 優化前后樣條質量對比

注：1.橡膠的密度以天然橡膠為例，取ρ=10-9t/mm3； 2. 樣條橡膠指直段1上的軟橡膠，整段橡膠的減重類似。

(2)構型2與構型3上每段橡膠的接觸壓力與原始模型相比有所提高，且兩者的變化趨勢曲線較為吻合。

(3)構型4上每段橡膠的接觸壓力與原始模型相比明顯有較大提高，但是考慮到構型4小圓半徑為1.1 mm，處于小圓與車門分離的臨界狀態，此時小圓上的接觸狀態較差。

若單從4種構型的減重效果分析，顯然構型4減重最多，其次分別是構型2和3，最小的是構型1。因此確定最終改良的新構型時，需要綜合考慮密封性和減重等綜合因素。

4 結論

駕駛門密封條是車輛裝備密封系統中十分重要的部件，良好的密封條截面設計對提高車輛的密封性及改善關門效果都有很重要的意義。因此對汽車密封條的結構、材料、壓縮變形及受力分析是很有必要的。采用有限元分析方法對密封條軟橡膠截面參數進行敏度分析，綜合考慮各參數的影響，進行了密封條構型改良設計。

針對4種設計方案，結合整體模型的受力情況和分段橡膠上的壓縮性能分析，研究了改良前后構型對密封性和減重方面的影響，得到有用的設計信息，以期為后續研發人員進行產品設計提供參考依據。