雙盤球式自動平衡裝置動態(tài)特性分析

郭文軍， 張小龍， 張 凱， 李 涵

(西安建筑科技大學(xué)機電工程學(xué)院，西安 710055)

由于回轉(zhuǎn)體不平衡的存在，產(chǎn)生強迫振動，且處于臨界轉(zhuǎn)速附近振動幅值增加。尤其對于高速旋轉(zhuǎn)機械，如離心機、汽車車輪[1]等，每次轉(zhuǎn)軸轉(zhuǎn)動時不平衡力大小隨機變化。對此旋轉(zhuǎn)機械也只能在運行時才能取得平衡。然而采用高精度的靜動平衡方法存在很大局限性，對于轉(zhuǎn)子質(zhì)量可能隨時發(fā)生改變的回轉(zhuǎn)機械，嚴(yán)重影響轉(zhuǎn)軸運行軌跡[2]。

旋轉(zhuǎn)機械中剛性轉(zhuǎn)子通過改變平面校正質(zhì)量對主軸進行重新校準(zhǔn)[3]。然而，諸如材料腐蝕以及熱變形的影響可能導(dǎo)致轉(zhuǎn)子質(zhì)量分布改變，并且在這種情況下必須重復(fù)平衡過程，會讓生產(chǎn)加工產(chǎn)生間斷性。這種限制促使人們開始對自動平衡裝置進行深入研究，重新分配轉(zhuǎn)子自身質(zhì)量以消除任何不平衡。自動平衡裝置能夠在轉(zhuǎn)子系統(tǒng)不停止工作的條件下，對轉(zhuǎn)子系統(tǒng)實現(xiàn)自動平衡。在現(xiàn)實生活中，球式自動平衡裝置已經(jīng)應(yīng)用在離心分離機、光盤驅(qū)動器等[4]許多領(lǐng)域。隨著對平衡裝置深入研究以及其實用價值的體現(xiàn)，應(yīng)用推廣將會被人們更加認(rèn)可。

該裝置結(jié)構(gòu)簡單，可行性強，使用價值較高，對此中外專家進行了許多理論與實驗驗證。為了消除轉(zhuǎn)子系統(tǒng)產(chǎn)生的有害強迫振動，將滾球加入在回轉(zhuǎn)體的圓盤來平衡轉(zhuǎn)子系統(tǒng)。當(dāng)轉(zhuǎn)子轉(zhuǎn)速達到臨界速度，離心力帶動滾球運動消除靜不平衡，達到減振目的，并證明了在第一臨界頻率以上時，轉(zhuǎn)子在該轉(zhuǎn)速下存在的穩(wěn)態(tài)機。Rodrigues等[5-7]對雙盤球式自動平衡裝置的穩(wěn)定性和分岔理論進行了分析與研究。張小龍等[8-9]運用了諧波平衡法解釋單、雙滾珠轉(zhuǎn)子系統(tǒng)在臨界轉(zhuǎn)速附近平面振動的動態(tài)特性，對比研究了單滾球與雙滾球平衡制振效果并進行數(shù)值計算與理論說明。通過理論解析與數(shù)值模擬,研究了兩滾珠平衡制振時轉(zhuǎn)子系統(tǒng)的1/2次分?jǐn)?shù)諧波振動的響應(yīng)特性及滾珠質(zhì)量對振動響應(yīng)大小的影響規(guī)律等。羅建等[10]利用病態(tài)性探測，得出了球式自動平衡裝置對作非平面運動的轉(zhuǎn)子減振效果顯著，平面振動與空間振動都得到了有效控制。譚青等[11]對球式自動平衡裝置進行了虛擬實驗研究，建立了虛擬實驗平臺，通過可視化實驗分析滾球平衡過程。目前研究主要以單盤球式自動平衡裝置為主，而實際上雙盤球式自動平衡裝置的應(yīng)用也在不斷增加。

針對Jeffcott轉(zhuǎn)子系統(tǒng)，在轉(zhuǎn)軸上固定兩個轉(zhuǎn)盤，在轉(zhuǎn)盤中各加入兩個滾球，通過理論說明與數(shù)值模擬，研究了雙盤球式自動平衡裝置的制振特性及盤中滾球運動規(guī)律。

1 數(shù)學(xué)模型簡要說明

在工程實際與生產(chǎn)應(yīng)用中，高速轉(zhuǎn)動轉(zhuǎn)子在不平衡力矩作用下，轉(zhuǎn)軸的運動范圍不僅僅在單一平面內(nèi)，整個系統(tǒng)會在非平面運動，產(chǎn)生空間上的力與位移。雙盤球式自動平衡裝置更加與實際貼合，該裝置的力學(xué)模型如圖1所示。在無質(zhì)量彈性軸的兩端(假設(shè)彎曲剛度為k)安裝有質(zhì)量為M1和M2的圓盤(Jeffcott轉(zhuǎn)子)，運動阻尼為C，每個圓盤內(nèi)有半徑為R的凹槽，凹槽內(nèi)質(zhì)量均為m(m?M1、M2)的兩個滾球，滾球的半徑為r，沿軌道半徑R的凹槽作圓周運動。

雙盤球式自動平衡裝置中一個圓盤的模型如圖2所示，設(shè)圓盤形心為O1(X,Y)、兩個平衡滾球角位置φi1和φi2，i=1,2。圖中白色圓代表滾球位置，黑色圓表示回轉(zhuǎn)體重心的位置。

圖1 雙盤球式自動平衡裝置力學(xué)模型Fig.1 Mechanical model of double-ball automatic balancing device

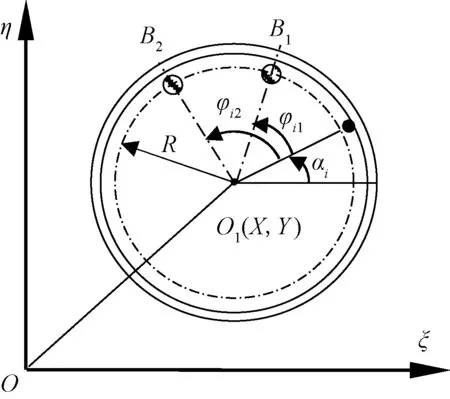
圖2 圓盤中滾球轉(zhuǎn)動模型Fig.2 Rolling ball rotation model in the disc

采用的符號如下(如未加特殊說明,單位均采用國際標(biāo)準(zhǔn)單位)：

O0-XYZ:靜止坐標(biāo)系，且與O1-X1Y1Z1平行。

O1εηξ為旋轉(zhuǎn)軸的動坐標(biāo)系。

O0O1為圓盤中心靜止時和運動時的位置。

O1為Ⅰ圓盤與旋轉(zhuǎn)軸的交點。

M1、M2、M為Ⅰ圓盤質(zhì)量、Ⅱ圓盤質(zhì)量、系統(tǒng)總質(zhì)量。

ω為轉(zhuǎn)子角速度。

L1、L2為Ⅰ圓盤、Ⅱ圓盤中重心偏移位置。

m、Ib、r為球的質(zhì)量、轉(zhuǎn)動慣量、半徑。

Iθ、Iψ為系統(tǒng)η、ξ軸上的轉(zhuǎn)動慣量。

φij為i圓盤j球的轉(zhuǎn)角(i=1,2；j=1,2)。

kr、Cr為轉(zhuǎn)軸的剛度、阻尼。

C0、C1為球的滾動摩擦系數(shù)，黏性阻尼系數(shù)。

R為球的公轉(zhuǎn)半徑。

Θ、Ψ為轉(zhuǎn)動軸角變化。

Ir為轉(zhuǎn)動軸的轉(zhuǎn)動慣量。

由圖1、圖2可知，雙盤球式自動平衡裝置可利用拉格朗日建立運動方程為

(1)

式(1)中：T為系統(tǒng)的總動能之和，包括圓盤Ⅰ、Ⅱ的動能，滾球的動能；qα為系統(tǒng)廣義坐標(biāo)；V為系統(tǒng)的總勢能；Qα代表廣義外力；s為坐標(biāo)數(shù)。由此推出雙盤球式自動平衡裝置運動方程為

(2)

2 定常解計算

對運動方程(2)進行無量綱化，得：

(3)

則方程(2)得到的系統(tǒng)方程式為

i=1,2；j=1,2

(4)

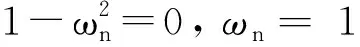
用平均法進行數(shù)值解析，式(4)的周期響應(yīng)為

(5)

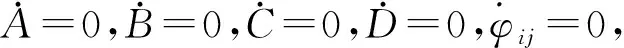
(6)

(7)

式(7)中：

(8)

式(8)中：ν=p的定常解如下。

5.1 穩(wěn)定解

滾球相對靜止，振幅為零。

(9)

此解僅存在0<δi≤2時，βi=cos-1(-δi/2)，各個圓盤及滾珠的位置如圖3所示。

當(dāng)ν=p，δi=0時，此時由式(9)得φi2-φi1=π，A=B=C=D=0，同樣振幅為零。此時δi=0，各個圓盤及滾珠的位置如圖4所示。

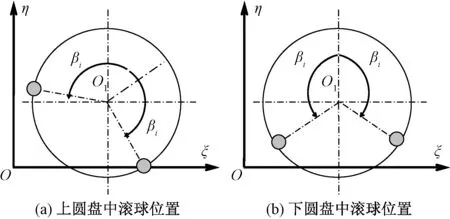
圖3 定常解的滾球位置Fig.3 Position of balls in the steady state solutions

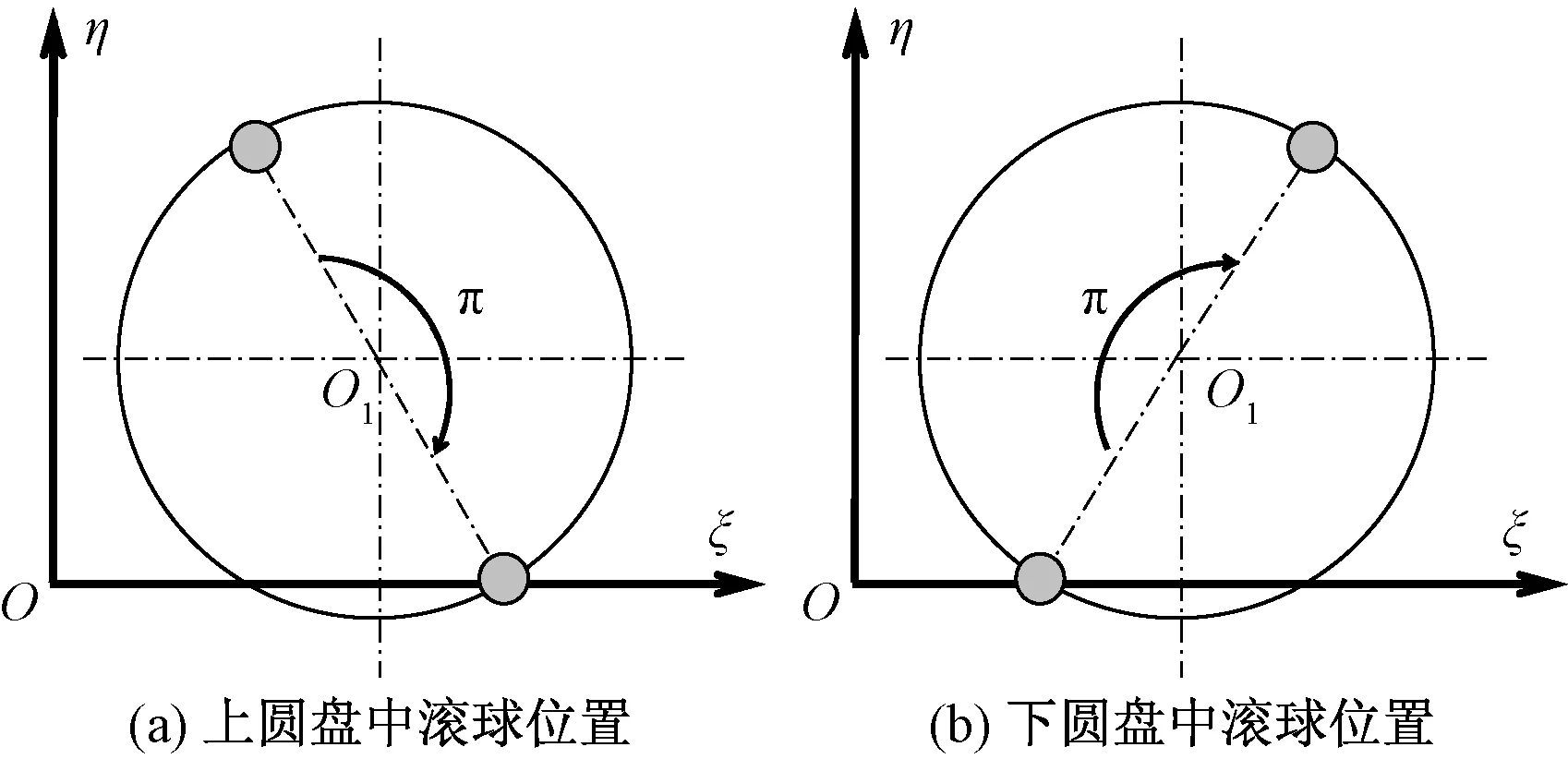
圖4 定常解的滾球位置Fig.4 Position of balls in the steady state solutions

(2)不穩(wěn)定解。滾球相對靜止，振幅不為零。

ν=p,φi1=φi2=φi(i=1,2)，此時A、B、C、D都不為零，即振幅不為零，系統(tǒng)不穩(wěn)定。如圖5所示。

圖5 定常解的滾球位置Fig.5 Position of balls in the steady state solutions

3 模型的數(shù)值仿真

3.1 數(shù)值計算原理

在求解常微分方程時，通常將高階方程降階求解。采用ode45對模型進行數(shù)值仿真。求解過程將運動方程的二階量變?yōu)橐浑A，符合龍格庫塔計算的具體要求。在這里方程式(3)中的μθ非常小，可以假設(shè)為零，僅僅研究響應(yīng)y及滾球的位置φ11、φ12、φ21、φ22。則方程(4)的具體形式可以表示為

(10)

為了確定上述定常解精確度，研究滾球出現(xiàn)的運動規(guī)律，對方程(10)數(shù)值計算。略去公式中高階小量O(ε2),選取合適仿真參數(shù)應(yīng)用于ode45,編寫仿真程序。對系統(tǒng)降階處理，去高階小量，得到系統(tǒng)的一階方程如下：

[S1,S2,S3,S4,S5,S6,S7,S8,S9,S10]；

(11)

3.2 滾球碰撞調(diào)整

球式自動平衡裝置中研究的核心部分是滾球，滾球運動時盡量避免互相接觸與碰撞，這樣可能影響運動軌跡，研究中需檢查確定滾球位置是否發(fā)生干涉，干涉嚴(yán)重且產(chǎn)生誤導(dǎo)性理論研究，須對滾球作碰撞處理。

滾道中的兩滾球之間的夾角φ大于夾角σ，此時σ表示兩滾球已經(jīng)相互接觸，兩滾球碰撞視為完全非彈性碰撞，即指滾球碰撞結(jié)束，在一瞬間內(nèi)兩物體運動狀況完全相同，獲得相等的速度，如圖6所示。

(12)

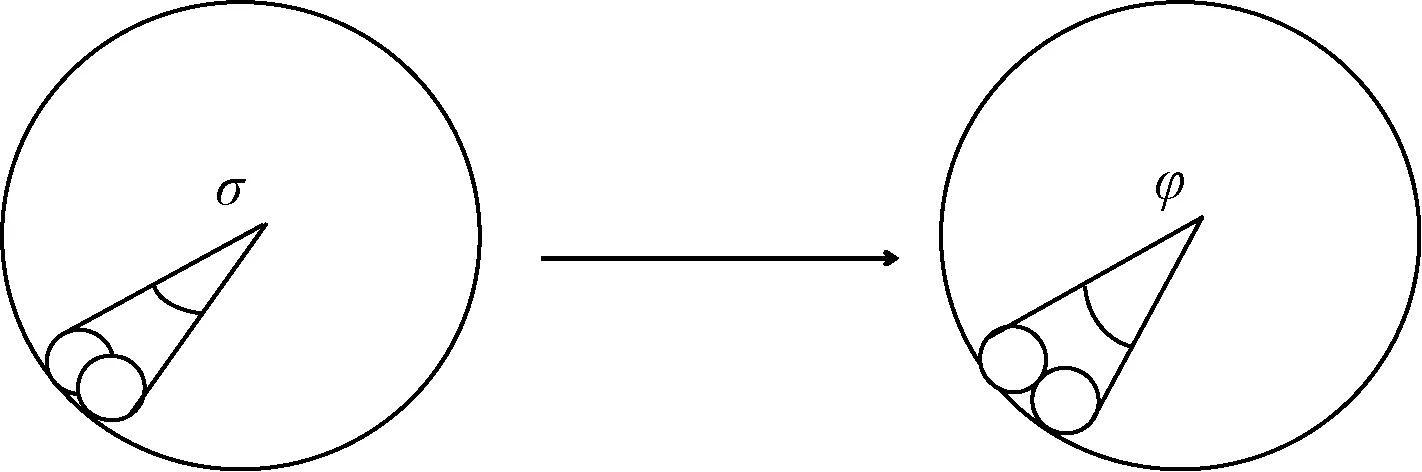
圖6 滾球碰撞調(diào)整Fig.6 Rolling ball bollision adjustment

3.3 數(shù)值仿真結(jié)果

基于MATLAB軟件利用龍格庫塔法對系統(tǒng)進行數(shù)值計算，仿真的角速度分布于高速區(qū)和低速區(qū)，在p=0.758 8、p=0.999 5、p=2.222 5時，出現(xiàn)的仿真結(jié)果與定常解的數(shù)值相對應(yīng)。

圖7 數(shù)值模擬結(jié)果(p=0.758 8)Fig.7 Numerical simulation (p=0.758 8)

角速度p=0.758 8時，響應(yīng)y及滾球的位置φ11、φ12、φ21、φ22如圖7所示。由于轉(zhuǎn)速p小于1，轉(zhuǎn)速較小，各個圓盤上的兩滾球相對于回轉(zhuǎn)體相對靜止，圖7(a)與圖7(b)所示，φ11=φ12≈27°，φ21=φ22≈27°(圖中穩(wěn)定時φ大約0.5 rad)。轉(zhuǎn)子y方向以角頻率p作單頻簡諧振動，且轉(zhuǎn)子振幅y方向的響應(yīng)并不收斂于零，如圖7(c)所示,在低速側(cè)，轉(zhuǎn)子振動幅值為-0.75～0.75，幅值較大，平衡效果不理想。

當(dāng)p=0.999 5，幾乎接近于臨界轉(zhuǎn)速1時，響應(yīng)如圖8所示，兩圓盤上的滾球各自收斂于同一位置，圖8(a)與圖8(b)中，φ11=φ12≈27°，φ21=φ22≈300°，相對于回轉(zhuǎn)體靜止不動，轉(zhuǎn)子y方向以角頻率p作單頻簡諧振動，但y方向的振動明顯增大，如圖8(c)所示，幅值為-1.8～1.8，導(dǎo)致振幅在定常解附近發(fā)生變化，產(chǎn)生強烈振動。

圖8 數(shù)值模擬結(jié)果(p=0.999 5)Fig.8 Numerical simulation (p=0.999 5)

在p=2.222 5，遠超過1時，響應(yīng)如圖9所示，滾球在回轉(zhuǎn)體圓盤內(nèi)對稱分布，圖9(a)與圖9(b)所示φ11=φ21≈120°，φ12=φ22≈-120°，轉(zhuǎn)速明顯增大，每個圓盤中兩滾球在偏心質(zhì)量反方向布置，如圖9(c)所示,轉(zhuǎn)子的振幅y逐漸趨于零，此時滾球位置驗證了式(9)求得定常穩(wěn)定解的準(zhǔn)確性，起到了平衡效果。

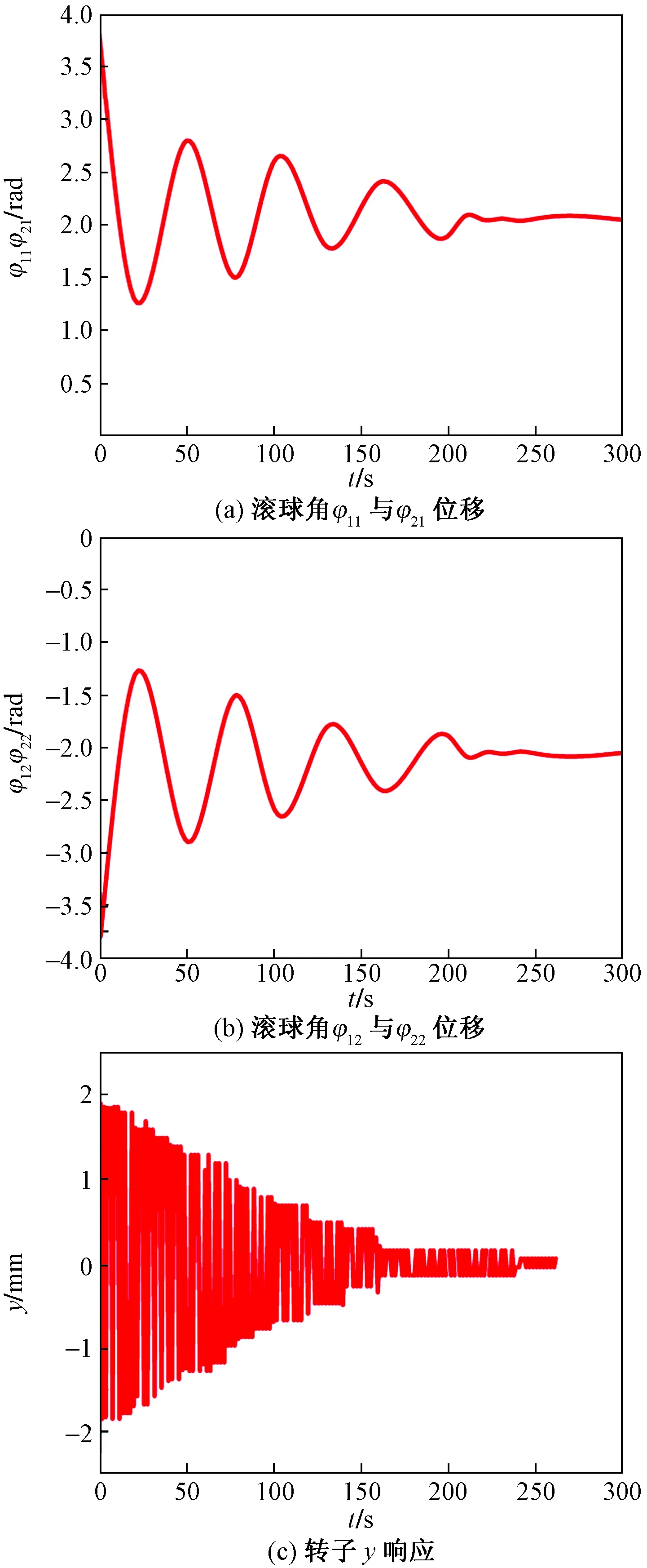
圖9 數(shù)值模擬結(jié)果(p=2.222 5)Fig.9 Numerical simulation (p=2.222 5)

仿真結(jié)果可以看出，在轉(zhuǎn)軸轉(zhuǎn)速較小時，或者接近于臨界轉(zhuǎn)速，每個圓盤內(nèi)的兩個滾球都會相對靜止，不會分開，且起不到減小振動的效果。只有在轉(zhuǎn)速遠遠大于臨界轉(zhuǎn)速時，圓盤中的滾球才會分布于偏心質(zhì)量相對面，起到平衡制振效果。

4 實驗驗證

為了驗證雙盤球式自動平衡裝置的有效性，設(shè)計了圖10所示的實驗平臺，著重研究穩(wěn)態(tài)時該裝置的減振效果以及滾球的位置。

改變電機的轉(zhuǎn)速來控制轉(zhuǎn)軸轉(zhuǎn)速，在不同轉(zhuǎn)速條件下，通過對比發(fā)現(xiàn)，仿真結(jié)果與實驗結(jié)果減振的趨勢基本一致，當(dāng)回轉(zhuǎn)速度較高時，自動平衡裝置的振幅將會變小，此時滾球的位置如圖11所示。

圖10 實驗平臺Fig.10 Experimental platform

圖11 滾球位置Fig.11 Ball position

實驗表明，工作轉(zhuǎn)速接近臨界轉(zhuǎn)速時，振動的幅值明顯增大。雙盤球式自動平衡裝置在超過臨界轉(zhuǎn)速時具有很好的平衡制振性能。

5 結(jié)論

對雙盤球式自動平衡裝置主共振振動響應(yīng)進行了研究，結(jié)論如下。

(1)雙盤球式自動平衡裝置的運動特性和滾球運動規(guī)律是，當(dāng)轉(zhuǎn)速接近臨界轉(zhuǎn)速時，轉(zhuǎn)子的振幅明顯增大。

(2)在轉(zhuǎn)速較低時，雙盤球式自動平衡裝置轉(zhuǎn)子振幅增大，平衡惡化。轉(zhuǎn)速較高時，發(fā)生穩(wěn)態(tài)振動，定常解始終有振幅為零的周期解，即該裝置在高速運轉(zhuǎn)時，可以自動消除不平衡。