基于有限元分析的無砟軌道結構通用模型研究

肖艷杰

摘 要 目前，無砟軌道結構已廣泛應用于鐵路建設中，為了確保軌道結構在運營過程中的安全性及實用性，有必要對其進行合理的結構設計，分析設計結構在荷載作用下的力學數值。在各類工程案例中，對無砟軌道的設計要求不盡相同，本文基于有限元分析法，借助自編有限元計算軟件創建出鋼軌位移及軌道板彎矩檢算通用模型，實現僅通過調整參數可對各類工程項目中不同鋼軌類型、不同軌道板寬、不同軌距等形式的無砟軌道結構進行仿真模擬分析。

關鍵詞 無砟軌道;有限元;軌道板;鋼軌位移

本文運用有限元原理，基于C語言進行有限元軟件編程，針對掌握的無砟軌道結構形式、幾何尺寸進行有限元模型的創建，并且對所建模型進行加載求解，在加載下進行力學數值分析，這對軌道板的配筋設計至關重要[1]。

1無砟軌道結構軌道板彎矩檢算通用模型的建立

本文依據彈性地基梁-板-板理論計算原理，本模型取相鄰的三塊軌道板長度的無砟軌道結構來建立有限元模型。考慮到計算模型的通用性，軌距、軌道板長度、底座長度等均設為可變參數[2]。

在本文中通用模型單元類型設計如下：

鋼軌為細長構件，用梁單元來模擬;扣件及其軌下膠墊部分利用彈簧連接來進行模擬;軌道板以及底座板均采用四節點非協調矩形薄板來進行模擬;CA砂漿層利用均布彈簧單元進行模擬。

本文無砟軌道結構通用模型中鋼軌類型可選擇國內鐵路設計中普遍采用的標準鋼軌，采用命令流的形式在自編有限元軟件中繪制鋼軌斷面圖，并對其進行網格劃分。

通用模型使用步驟簡述如下：

選擇具體項目中采用的鋼軌類型并進行軌道結構模型的創建，定義材料屬性，為保證模型的通用性，對軌道板、底座進行網格劃分時，每條邊按分段數劃分。

如上文所述，鋼軌、軌道板利用彈簧形式模擬扣件來進行聯結，軌道板和底座板之間也用彈簧聯結，但兩層彈簧剛度需根據工程實際分別設置，底座板與地基固定聯結。

為保障通用模型的準確性，須對此模型進行一定的約束設置：首先應該對軌道板進行縱向位移的約束;其次還應對底座板進行全約束;最后對鋼軌進行約束，本模型采用置大數法（×10E10）模擬約束，鋼軌在X軸和Y軸方向上的位移是零，并且其不能圍繞Y軸作旋轉;對CA砂漿下部采用刪行刪列法模擬約束[3]。

本模型可以通過改變模型參數，選擇軌道板長度范圍內任意對輪對進行加載，荷載大小可調;加載完成后此計算程序可分別求解得出該研究結構的結果圖，其中包括軌道板的變形圖、底座板變的形圖、應力云圖、軌道底板底座板的縱橫向彎矩圖等。

2通用模型在無砟軌道結構中的應用

2.1 選用無砟軌道參數

鋼軌彈性模量2.1×1011 Pa，泊松比0.3，高度0.176m;軌道板彈性模量3.65×1010 Pa，泊松比0.2，厚度0.19m;底座板彈性模量3.4×1010 Pa，泊松比0.2，厚度0.3m;扣件彈性模量2.1×1011 Pa，泊松比0.3。

2.2 鋼軌位移及軌道板彎矩計算結果

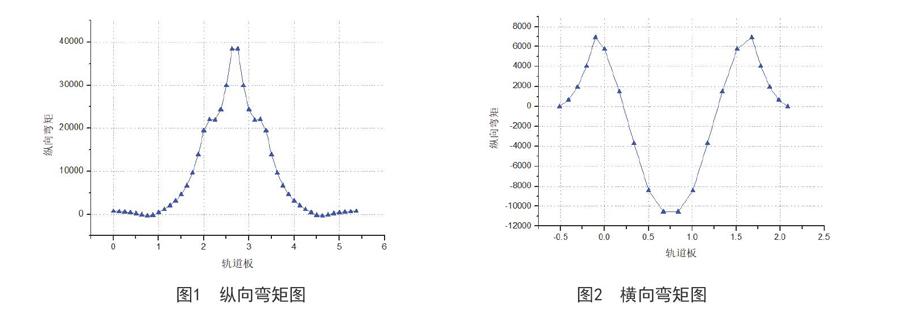
依據已掌握的無砟軌道結構形式、幾何尺寸進行有限元模型的創建，依據已知結構特性、材料參數進行單元定義，結構層間的聯結在建立好之后，進行加載求解。軌道板計算結果如下圖所示：

軌道最大位移2.315mm，軌道板橫向最大彎矩10548.99N·m/m，軌道板縱向最大彎矩38621.54 N·m/m。

3結束語

本文基于無砟軌道力學理論模型建立有限元無砟軌道通用模型，本模型適用于不同軌距、鋼軌類型、軌道板寬度等無砟軌道結構形式，其計算結構精確可靠，高效簡便，適用性較廣，可廣泛應用于工程項目中軌道板的制作及其預應力配筋工作。

參考文獻

[1] 趙國堂.高速鐵路無砟軌道結構[M].北京：中國鐵道出版社，2006： 109.

[2] 王其昌，韓啟孟.板式軌道設計及施工[M].成都：西南交通大學出版社，2002：27.

[3] 陳希成.板高速鐵路板式軌道力學分析[D].成都：西南交通大學出版社，2008.