基于有向圖的評分改進算法設計與實現

陳佳伊，李紅波，崔偉燦，王 吉，應正波

（浙江中控技術股份有限公司，杭州 310053）

0 引言

一所現代化工廠成功的一個重要因素就是具有較高技術水平和豐富經驗的現場操作人員。傳統的師傅帶徒弟的一對一培訓模式由于效率低下，已經逐漸被淘汰，采用虛擬控制仿真培訓系統不僅可以大大提高培訓效果，節省培訓費用，縮短培訓時間，而且可以降低裝置操作的不確定性，減少或避免事故發生。同時仿真培訓可以培養一人多崗，一專多能的高素質人才，為企業的長期發展提供人才保障，是國內外公認的煤化工、石油化工等領域最高效的現代化技能培訓與考核手段。

目前OTS 仿真培訓的評分算法采用的是單向鏈表的數據結構，評分規則單一，對評分配置的限制諸多，難以滿足工程上對于評分規則靈活性的要求。本文提出了一種評分關系依賴模型，改進了評分規則算法，使得工程實施時的靈活度和便利性大大提高。

1 建立評分關系依賴模型

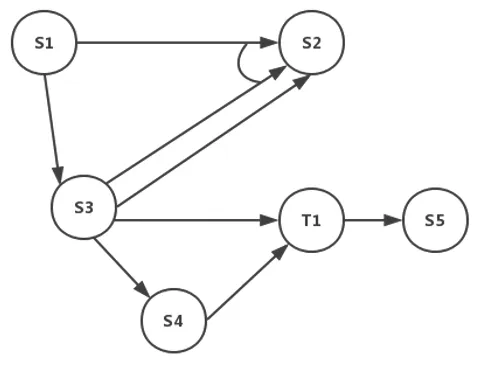
圖1 有向圖表示步驟間依賴關系示例圖Fig.1 An example diagram of a directed graph of inter-step dependencies

在培訓過程中，教員使用評分組態軟件設計一套評分規則對學員的現場操作進行考察，構成評分規則的基本元素為評分步驟。步驟表示操作員的一個操作動作，不同步驟根據不同的規則組合在一起，用于評定操作員的操作順序是否正確，操作是否達到預期目標。

一個步驟可以抽象為有向圖中的一個節點，在此將步驟記為S。步驟與步驟之間存在依賴關系，依賴關系的類型有時間關系、順序關系和引用關系。時間關系用于考察兩個關聯的步驟是否在設定的時間關系內完成，順序關系考察兩個關聯的步驟是否按照設定的次序被執行，引用關系表示一個步驟引用另一個步驟的狀態作為該步驟的評分依據。例如，步驟2 引用步驟1 的完成狀態作為該步驟開始的條件。

步驟的最終計算結果與步驟間的依賴關系有關，步驟的時間關聯和順序關聯也可抽象為有向圖中的一個節點，分別記為T 和O，引用關系和函數關系以箭頭方式表示。在評分關系依賴模型中存在多個依賴關系確定步驟狀態的情況，記為{O,T-＞S}，其中O,T-＞S 的含義即為順序依賴關系O 和時間依賴關系T 共同確定步驟S 的狀態。圖1 表示了這種依賴關系，其中用圓弧連接兩條有向邊表示節點間存在“與”的關系，“或”關系未在圖中做出特殊標記。

2 評分算法的設計與實現

2.1 構建最小函數依賴集

步驟的規則屬性間存在函數依賴關系，該函數依賴關系反映了規則屬性間的關聯性和數據的完整性約束。而由于各步驟規則屬性間存在錯綜復雜的依賴關系，為了使依賴關系簡單、明了，減少在實際運算過程中的重復運算，首先需要求解模型的最小函數依賴[1]集以簡化運算。在求解最小函數依賴集的過程中，傳統的算法能解決相應問題，但不夠直觀，將有向圖的表達運用到函數依賴關系中去，會使得問題的求解更加清晰、直觀。

下面給出最小函數依賴集F'的求解算法：

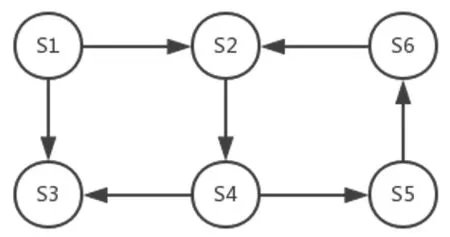
圖2 深度遍歷模型示例圖Fig.2 Depth traversing model sample

1）根據函數依賴集F，畫出步驟間依賴關系的有向圖，其中各節點表示各個步驟或時間、順序關系、引用關系，有向邊表示函數關系，有向邊箭頭的起始結點為決定因子。

2）考察圖中每條邊，如果出現平行邊，則刪除存在“與”的關系的那組邊，由于在函數依賴集中不會出現完全相同的函數依賴關系，所以這里的平行邊只會存在于一條獨立邊與一組“與”邊中的其中一條。

3）如果圖中某個結點到達另一個節點的路徑有多條，則刪除直接相連的邊，保留經過其他節點到達的邊。經過簡化后，消除了由傳遞函數依賴導致的多余函數依賴。

4）將變換后的圖中屬性間的關系轉換為函數依賴關系的表達，得到的函數依賴集即為最小函數依賴集F'。

2.2 環的存在與檢測

得到步驟關系依賴圖，在對步驟進行拓撲排序前，需要對步驟間的依賴關系進行環路檢測，保證得到的步驟關系依賴圖是一個有向無環圖[2]。如果存在環路，步驟間接引用自身的狀態將會導致死循環。例如，步驟1 引用步驟3 的考試結束狀態作為步驟開始的條件，步驟3 引用步驟2的考試結束狀態作為步驟開始的條件，步驟2 又引用步驟1 的考試結束狀態作為步驟開始的條件，此時步驟1 又去獲取步驟3 的考試狀態，造成死循環。

這里采用著色法檢測有向圖中是否存在環路，檢測算法如下：

1）分別對每個節點進行深度遍歷。

2）對每個節點的狀態進行標記，白色代表此節點還沒有被處理；灰色代表此節點正在被處理，或者說他的兒孫們還沒有被處理；黑色代表此節點以及其所有兒孫都已經被處理過了。

3）在深度遍歷時，如果到達了一個灰色的節點，說明該有向圖中存在環路。

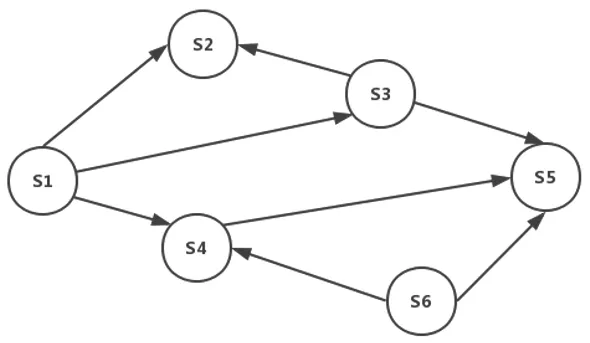
圖3 評分關系模型示例圖Fig.3 An example of scoring relationship model

以圖2 為例，以深度優先搜索S1 節點時，先將S1 標記為灰色，依次尋找子節點得到S1-＞S3，到達S3 節點時發現不存在子節點，將S3 標記為黑色。繼續搜索得到S1-＞S2-＞S4-＞S3,到達S3 節點時發現不存在子節點，將S1、S2 標記為黑色，此時對S1 節點搜索完畢，繼續搜索S2 節點，先將S2 標記為灰色，依次尋找子節點得到S2-＞S4-＞S5-＞S6-＞S2，此時S2 的狀態為灰色，該圖中存在環路。

2.3 建立拓撲序列圖

以下面的評分關系模型為例，如圖3 所示。

在未經排序優化前，步驟根據默認的順序進行計算，過程如下：

1）計算得到S1 的評分結果。

2）對S2 進行評分計算-＞獲取本輪評分中S1 和上一輪評分中S3 的結果-＞得到S2 的結果。

3）對S3 進行評分計算-＞獲取本輪評分中S1 的結果-＞得到S3 的結果。

4）對S4 進行評分計算-＞獲取本輪評分中S1 和上一輪評分中S6 的結果-＞得到S4 的結果。

5）對S5 進行評分計算-＞獲取本輪評分中S3 和上一輪評分中S4、S6 的結果-＞得到S5 的結果。

6）對S6 進行評分計算-＞獲取本輪評分中S4、S5 的結果-＞得到S5 的結果。

由此可見，采用默認的計算順序會導致評分計算輪次混雜，步驟的依賴數據未更新，甚至出現引用同一個步驟得到的計算結果不一致的問題，而實際應用中的模型遠比上述模型復雜的多，更容易出現難以預料的結果。建立拓撲序列圖[3]，對評分中的最小元素進行計算順序的排序可以規避這種問題，拓撲排序算法如下：

① 在步驟關系依賴圖中選一個沒有前驅節點的節點并且輸出。

② 從圖中刪除該節點和所有以它為尾的邊。

③ 重復上述兩步，直至所有節點輸出，或者當前圖中不存在無前驅節點的節點為止，最后得到整理好的拓撲序列。

以圖2 的關系模型為例，展示拓撲排序過程：

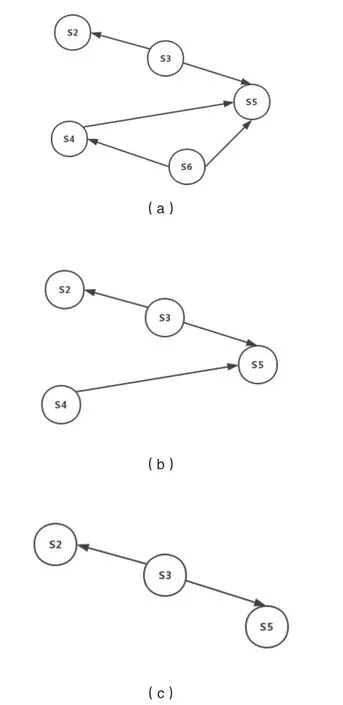
圖4 變換后的步驟關系圖Fig.4 Transformed step diagram

首先，發現S6 和S1 沒有前驅節點，隨機選擇一個輸出，這里選擇先輸出S1，刪除和S1 有關的邊，得到如圖4(a)所示結果。

然后，繼續尋找沒有前驅節點的節點，發現S6 沒有前驅節點，輸出S6，刪除和S6 有關的邊，得到如圖4（b）的結果。

然后，又發現S4 和S3 都是沒有前驅節點的，這里選擇先輸出S4，得到如圖4（c）結果。

然后，繼續輸出沒有前驅節點的S3，此時只剩下兩個沒有前驅節點的節點S2 和S5，輸出S2 和S5。最后全部節點輸出完成，整理得到該圖的一個拓撲序列為：S1-＞S6-＞S4-＞S3-＞S2-＞S5。

此時按照拓撲順序依次計算步驟狀態，可以保證步驟引用的每個依賴數據都是本輪次的最新數據。

3 結論

本文提出了一種基于有向圖的工業仿真培訓系統評分關系依賴模型，解決了在評分計算中的步驟狀態循環引用檢測問題，提高了評分規則設置的靈活性。同時對原有的評分算法進行了改進，提出了一種計算順序重排算法，解決了在同一輪次中計算結果不一致的問題，規避了風險。