在深度教學中引發學生的數學思考
王霞飛


子曰:“學而不思則罔,思而不學則殆.”這說明學習思考的重要性.《義務教育數學課程標準(2011年版)》在課程目標的總體目標中明確指出“通過義務教育階段的數學學習,學生能夠初步學會運用數學的思維方式去觀察、分析現實社會,去解決日常生活中和其他學科學習中的問題,增強應用數學的意識”,并把“數學思考”作為小學生數學學習的四大目標之一.可見,培養小學生的數學思考能力單靠教師淺層次的課堂教學是無法實現的,只有教師深度地教,學生深度地學,不斷地提高課堂教學的品質、豐富課堂教學思維的內涵、創建有效的課堂教學活動,才有可能引發學生學習數學的思考能力.
如何在深度教學中引發學生的數學思考呢?我認為可以聚焦以下幾個方面.
一、關注學生的認知起點,學會思考
美國教育心理學家奧蘇伯爾在《教育心理學》一書的扉頁中指出:“如果我們不得不將教育心理學還原為一條原理的話,我將會說,影響學習的最重要因素是學生已經知道了什么,我們應當根據學生原有的知識狀況進行教學.”因此,數學教學活動必須建立在學生的認知發展水平和已有的知識經驗基礎之上.那么,在教學實踐中,教師該如何把握學生的學習起點呢?
例如,教學“除數是整十數口算除法”,課件出示教材生活情境圖,通過學生觀察、思考得出口算“80÷20”這一算式,學生會怎么樣算出結果呢?這時教師引導學生通過小組合作,借助已有的認知,歸納得出不同的口算方法.
1.動手操作法:這時最原始的方法.
10根小棒一捆,80根小棒8捆,再兩捆放一堆,可以放四堆,所以80里面有4個20,80除以20就得4.
2.乘法逆推法:算除法、想乘法.
4個20是80,80除以20得4.
3.合并計數法:把80想成8個十,把20想成2個十,8個十除以2個十得4.
4.遷移類推法:因為8÷2=4,所以80÷20=4.
通過借助學生原有的生活和學習經驗,總結出了“除數是整十數口算方法”,可以用動手操作法、逆推法、遷移類推法和合并計算法,得出80除以20的結果.同時,學生在獨立應用豎式驗算80÷20時,商4都寫在了個位上,并會總結出筆算兩位數除以整十數的計算方法.深度教學提倡用各種方式了解學生已有的知識經驗,再根據這些“前經驗”對所學知識進行加工,尋找學生學會、會學、易學的有效途徑,讓學生學會自己思考數學問題.
二、深入挖掘教學知識,拓展思考
《教材》是教師進行教學的依據,是教師用來教學的材料,也是學生用來學習的材料.教師使用教材需要教育的智慧.在新課程改革中,教師不是教教材,而是要用教材教.這不僅是一個教學理念的轉變問題,而且是一個教學實踐的操作行動問題.在教學實踐中,教師要深入挖掘教材編寫的真正意圖,它的變化以及發展趨勢.宏觀上,整體把握現行教材各個版本,理清所使用教材的編排特點與編排體系.微觀上,對教材所涉及的知識點、各領域知識結構的內在和分布情況進行細致的研究,達到觸類旁通.只有將教材了然于胸,才能確定好教學的重點與難點,找準教學的切入點,發展學生思維.決不能照葫蘆畫瓢,以至于誤人子弟.
例如,學習了兩位數乘兩位數筆算乘法之后,像65×54=3 510,這道題的結果正確嗎?許多學生會想到進行驗算,并呈現以下方法:
84×65=5 460 5 460÷65=84 5 460÷84=65
一般情況下教師講到這里就止步了.這時筆者追問學生除了上面方法之外,還要別的驗算方法嗎?看誰見多識廣!一石激起千層浪,一名學生說:“老師,我看過課外書,可以推薦一種更好的方法給同學參考.”筆者抓住時機讓他上臺展示,他有條有理地展示了自己的想法.
1.在黑板上畫一個大叉.
2.把一個因數乘數各位上的數字加起來,如果得到的數是兩位數,再把這兩個數字加起來.如上面被乘數是84,8+4=12,1+2=3,然后把3寫在右邊,如3.
3.把另一個因數也按照上面的方法加起來,6+5=11,1+1=2,把2寫在左邊,如23.
4.把積5460也按照上面說的方法加起來,5+4+6+0=15,1+5=6,寫在的上邊,如23.
5.再把23左右兩邊的數字相乘寫在23,如果左右兩邊相乘是兩位數,也要按照上面說的方法加起來,寫在下邊.
經過以上思考,得出上下數字相同,就表明結果是正確的,否則就是錯誤的.
學生接著用這種方法驗算下面題584×275=160 600,發現這種方法很好,容易接受、理解.
在深度教學中,教師重視啟發學生挖掘教材資源的潛力,凝聚優質教學資源,注重挖掘教材的深度,拓展學生的數學思考,有利于培養學生的數學思考能力.
三、力求知識結構化,優化思考
知識系統化是把零碎的知識形成知識網絡結構,包含兩層意思學習內容系統化和學習方式系統化.深度學習要力求讓知識學習和能力的培養達到結構化,讓學生學得輕松,學得系統.
如何讓知識的學習結構化?教學中教師要設計一些有趣的數學活動,簡化一些繁雜的教學流程,讓教學結構簡單化,并給予學生足夠時間和空間,圍繞優化學生思考方法去展開教學.
比如,在“雞兔同籠”教學中,教師緊緊抓住數量關系這個核心,讓學生根據教材展開教學,一步一步優化思考方法.
為了研究方便,依據教材把原題的數字改小一點:籠子里有若干只雞和兔,從上面數,有8個頭;從下面數,有26條腿.雞和兔各有幾只?
先讓學生理解關在籠子里雞和兔給我們帶來的數學信息:① 雞和兔共8只;② 雞和兔共有26條腿;③ 雞有2條腿;④ 兔有4條腿.
在理解題意,獲得信息之后,學生進行解答.
1.猜一猜,嘗試探究
生1:有3只兔,5只雞,可是算出來的腿是4×3+2×5=22(條),比實際的要少.
生2:如果有4只兔,4只雞,算出來的腿是4×4+2×4=24(條),比實際的還是少了.
師:很不錯!算得很有道理.但我們發現,盲目、凌亂猜不容易找到正確的答案.
生3:那我們按照順序列表吧!
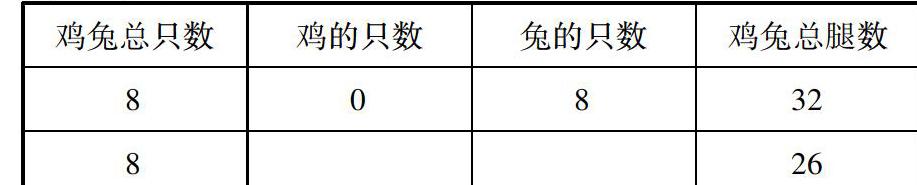
2.按照順序列表解答.
師:請同學們仔細觀察表格,想一想你有什么發現?
生4:每減少1只雞,增加1只兔,腿就增加2條.
生5:像剛才猜測時22條腿,我們只要把雞換成兔,因為比實際少了26-22=4(條)腿,只要把2只雞換成2只兔就可以了,因為1只雞比1只兔少2條腿,這樣雞就是3只,兔就是5只.
生6:哦,明白了,每把1只兔換成1只雞,總腿數就增加2條;換2只兔增加4條.換3只增加6條,換4只增加8條……
師:那我假設全是兔呢,就應該有32條腿,與實際26條腿相比,多出32-26=6(條),那我應該增加雞還是兔呢?增加幾只?
生7:因該增加雞,增加6÷2=3(只).
師:要是全是雞呢,總腿數是16條,比實際少了26-16=10(條),需要怎么調整?需要調整幾次?
生8:需要增加兔,調整10÷2=5(次),也就是增加5只兔.
在猜測的基礎上,引導學生思考這種方法不恰當.再在猜測的基礎上,讓學生一一列表,從無序思考到有序思考,發現其中隱藏的規律,發現規律的變化,學生對規律有了一定的感性認識,再引導學生上升到抽象的假設法,學生在理解假設法同時也溝通了各種方法之間的內在聯系,一步一步將知識結構化,幫助學生積累活動經驗,把握解題策略,優化思考方法.
總之,用深度教學的行動去引發學生學習數學思考,需要教師從學生的已有的經驗出發,尊重學生的認知規律;需要教師對學生的學習方式進一步探究,深入挖掘教學知識,拓展學生的思路;更重要的是還需要教師對知識結構的深入思考,引導學生用數學的眼光去觀察、分析、解決現實生活中的問題,構建有兒童味的數學課堂體系.只有這樣,才能讓深度教學真正引發學生的思考,體現數學教學的價值.

