重力壩壩基多斜面抗滑穩定模糊體系可靠度研究

錢 龍，王 剛，李夢瑤，李向鵬

(大連理工大學 水利工程學院， 遼寧 大連 116024)

對于混凝土重力壩，壩基深層抗滑穩定研究是其結構安全可靠性分析的重要一環[1]。重力壩壩基巖體失穩可能包含多種失穩通道(或路徑)，而將具有多失穩通道的基巖視為體系可靠度模型中的串并聯系統將更加符合工程實際[2]。同時，工程實踐和理論分析表明，決定重力壩壩基穩定可靠性的幾何與物理力學參數、失穩準則中的安全系數允許值等往往存在多種不確定性，它們的取值邊界通常并不十分清晰，即存在一定程度的模糊性。抗滑穩定計算參數的隨機性、模糊性以及失效準則的模糊性是重力壩抗滑穩定模糊體系可靠度分析中要考慮的問題[3-4]，也是當前大壩安全與可靠性研究中的難點問題之一。因此，將體系可靠度與模糊理論結合，對隨機與模糊不確定因素組合下重力壩的抗滑失穩問題進行研究，是完善重力壩設計理論的重要基礎性理論工作，也是保障重力壩安全穩定運行的重要技術手段。

目前在結構體系可靠度研究方面，主要有寬窄界限法[5]、主次結合法[6-7]等；在巖土工程模糊可靠度研究領域，主要是選用合理的隸屬函數分別對巖土穩定參數和失效準則(極限狀態方程)進行模糊化[8]，通過考慮不同隸屬度，得到數個可靠指標的模糊區間，并通過加權平均法來對這些區間進行處理[9]。本文將模糊理論與體系可靠度方法相結合，綜合考慮重力壩抗滑穩定參數及失穩準則的隨機模糊性，從而進一步深入研究多斜面、多滑移通道復雜重力壩壩基抗滑失穩評價理論，雖然本文研究成果是基于某一重力壩工程實例，但研究方法和研究思路仍具有普遍意義上的科研與應用價值。

1 重力壩抗滑穩定模糊可靠度

1.1 隨機變量的模糊截集處理

工程實際表明，巖土強度參數(變量)可以用有界正態隸屬函數表示其模糊性[10]，模糊隸屬函數大多服從數值為正值的近似正態分布，即：

(1)

式中：mx、σx為巖土樣本平均值和標準差的估計值；k為隸屬函數的取值參數，在邊坡工程一般取0.5～3.0[11]。本文主要討論影響重力壩可靠度的兩個重要因素，抗剪斷摩擦系數f′和黏聚力c′[12]。

1.2 失效準則界限模糊的隸屬函數

模糊理論假定穩定狀態到失穩狀態之間存在模糊區間，反映到失效準則上，即是安全系數容許值不確定，可將極限狀態方程變為[13]：

(2)

(3)

式中：λ為隸屬度；α是極限狀態的最大容差值，其取值主要參照以往工程經驗，邊坡工程中可取α∈[0.01,0.10]。

1.3 考慮模糊失效概率界限比的模糊可靠度

利用水平截集法可以將模糊極限狀態方程變為經典極限狀態方程，求解可靠度β的區間值。若要得到一個確定性的值，可取多個隸屬度λ，將得到的多個失效概率區間的上下界值通過加權平均得到模糊隨機可靠指標，但前提是失效概率區間的上、下界差距不宜過大。邊坡工程中一般取λ∈[0.75,1.00]，當λ<0.75時，失效概率計算結果將過于分散從而導致沒有實際意義上的參考價值。

目前關于式(1)和式(3)中隸屬函數參數k和α取值的研究成果較少。事實上，由于大壩工程的失效概率相對較小，研究工程模糊體系可靠度時，隸屬函數的不同形式、隸屬函數中參數k和α的取值、隸屬度λ的取值，都會導致結果出現較大的差異，為了得到更具有確定性的研究結論，本文提出模糊失效概率界限比的概念。

以R模糊失效概率上下界比值，即

(4)

對于某一失效事件，當失效準則隸屬函數的隸屬度λ一定時，R的變化能代表隨機變量的模糊區間范圍的大小，R=1時，即不考慮變量的模糊性，而當R>1時，R值越大，變量模糊區間范圍越大。

如果工程中存在n個相互獨立的失效事件，具均有模糊性，其中以Ri表示因素i(本文指隨機變量和失效準則的模糊)對R的影響，對于所有事件則有：

(5)

根據前文定義，若Ri=1，即不考慮因素i的模糊性影響。

對于具有兩個模糊因素的問題，用比值Rij=Ri/Rj來代表兩者在整體模糊隨機失穩事件中所占的比重，可知Rij范圍為[1/R,R]，數值越大因素i的模糊性占的比重越高，其上、下界分別代表失穩概率的模糊性完全由因素i決定和完全由因素j決定。

通過規定Ri的值，可以得到對應因素i模糊隸屬函數中參數如k或α的具體取值，并進行工程模糊可靠度分析研究，從而得到關于不同因素模糊性占比、隸屬函數形式以及隸屬函數中參數選定等的定量分析結論，從而保證當調整模糊隸屬函數參數k和α時也能將考慮失效準則模糊性的加權平均法用于重力壩抗滑穩定模糊可靠度計算。

2 重力壩抗滑穩定體系可靠度

為便于描述，我們規定，當重力壩基巖中存在多條滑移通道時，將每條滑移通道分別視為壩基抗滑穩定可靠度計算時的一種失效模式，當不同滑移通道之間具有共用滑移面時，各失效模式之間將具有一定的相關性，這時，多條滑移通道可作為可靠度計算的串并聯體系考慮。

2.1 體系可靠度的計算

(1) Ditlevsen窄界限法。主要考慮兩兩失效模式間的聯合分布的概率，利用概率論得到體系可靠度界限公式，其形式如下：

(6)

式中：Pfi是事件Ei的失效概率；P(Ei∩Ej)是第i和第j這兩個失效模式同時失效的概率，其計算參考文獻[11]。

Ei和Ej之間的相關系數ρEiEj，可以通過下式求得：

(7)

式中：αik、αjk是第i、j個失效模式xk中隨機變量的靈敏度系數，使用驗算點法求得，對于無法求偏導的復雜功能函數，可借助智能優化算法求解[14]。

(2) 主次結合法。結構體系的失效通常是由少數幾個主要失效模式引起的，只考慮主、次失效模式的相關性，對Ditlevsen窄界限公式簡化得到模型如下：

(8)

式中：Rs是結構可靠概率；ρ12是主次事件的相關系數；式(8)中R0.6計算見下式：

(9)

(3) 蒙特卡洛法。蒙特卡洛法通過對示性函數進行變更來解決體系可靠度問題，若存在m個失效模式的串聯體系，將示性函數變為：

(10)

式中：I[gi(x)]表示第i個失效模式的示性函數，多個gi(x)之間應存在共用隨機變量的情況，這代表了失效模式間的相關性。

2.2 考慮模糊性的體系可靠度計算

若結構體系的基本結構形式不發生變化，則其整體失效程度會隨著其中任一模式失效程度的變化而變化，在重力壩抗滑穩定可靠度分析中，單個滑移通道的模糊可靠度上、下限值對應著模糊體系可靠度的上、下限值。

3 工程算例

3.1 工程概況

某已建重力壩，其壩頂高程為2 564.00 m，最大壩高119.00 m，正常蓄水位和下游水位分別為2 560.00 m和2 471.61 m，淤沙高度52.7 m，取滲透揚壓力系數為0.25，某一典型河床壩段的巖基內存在較多的緩傾角軟弱結構面。存在五個潛在滑移面，E-F、F-G、G-B、D-F、G-C，這些滑移面共組成四條滑移通道，分別為DFGB、DFGC、EFGB、EFGC。該大壩工程抗滑穩定目標可靠指標值為3.7。本文僅考察基巖內結構面抗剪斷參數的不確定性。抗滑穩定可靠度計算時，使用正常蓄水位條件下的荷載組合，即需要考慮大壩和巖體的自重、上下游水壓力、揚壓力、浪壓力、淤沙壓力等作用的組合，且均為定值。

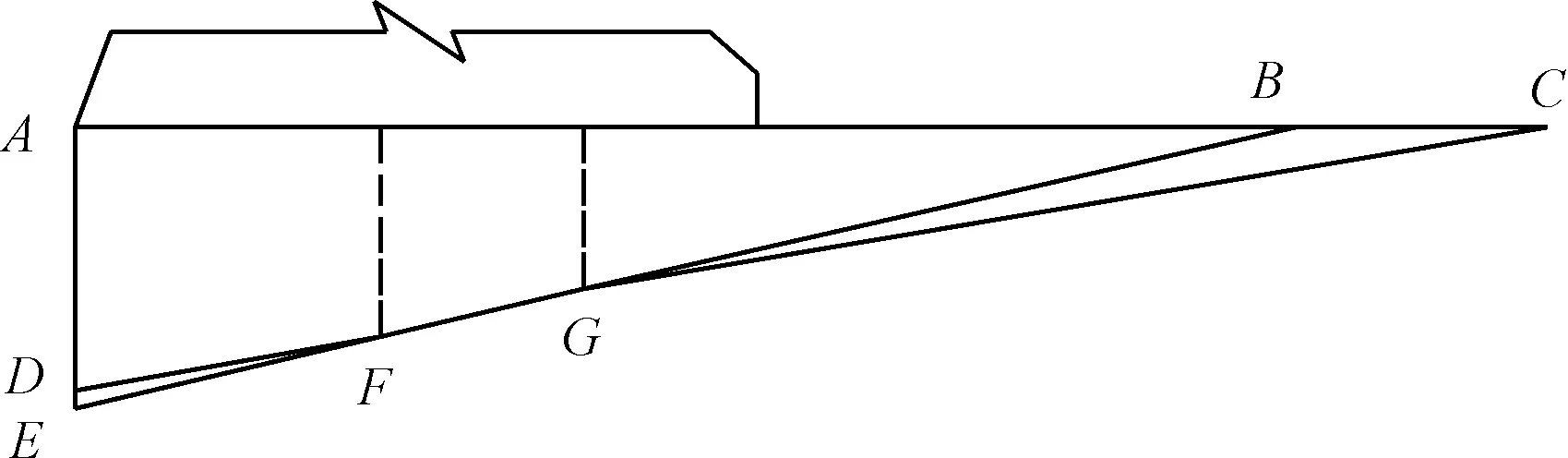
圖1 滑移通道示意圖

根據現場實測統計資料和已有文獻對抗剪斷強度參數統計特征的規定，基巖內各滑移面上抗剪斷摩擦系數f′和黏聚力c′取值和概率分布特征如表1所示。

3.2 體系可靠度計算

根據文獻[15]，使用剛體極限平衡法構建多斜面情況下的極限狀態方程，由于安全系數K的計算需要求解非線性方程組，對應可靠度計算的功能函數為非線性隱式功能函數。在本文作者之前研究工作的基礎上，可使用差分進化算法[16]求解單個滑移通道的可靠指標和對應的驗算點，為便于說明問題實質，這里只考慮f′和c′相關系數ρf′c′為0.0和-0.3的兩種情況。當ρf′c′為0.0時可得到滑移面EFGB、DFGB、EFGC、DFGC的可靠指標分別為4.116、3.787、4.214、3.909。給滑移面失效模式編號1、2、3、4，作為兩兩之間相關系數ρij的下標，如EFGB和DFGB失效模式的相關系數為ρ12，利用式(7)得相關系數表如表2所示。

表1 基巖結構面參數的統計特征

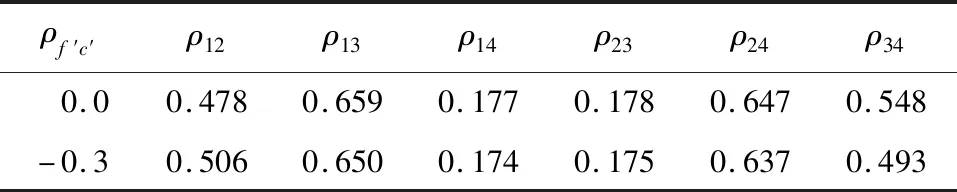
表2 失穩模式相關系數表

使用Ditlevsen二階模型法，主次結合法，蒙特卡洛法，分別進行體系可靠度計算，計算結果見表3。

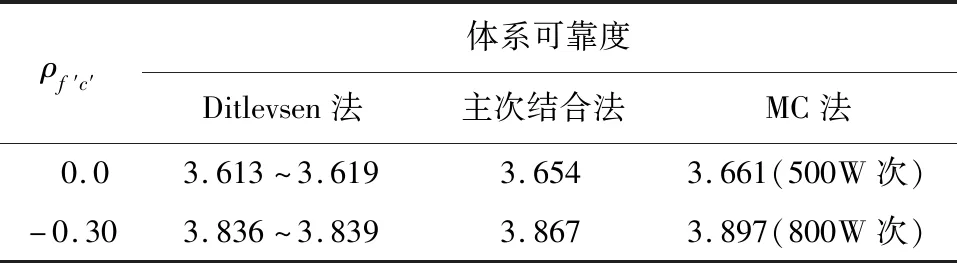
表3 體系可靠度計算結果對比

根據計算結果可知，當ρf′c′=0.0時，雖然單一滑移通道均滿足目標可靠指標β=3.7的要求，但體系可靠度并不滿足，可見基于多條滑移通道考慮基巖抗滑穩定體系可靠度是非常必要的；當隨機變量存在負相關性時，體系可靠度增加；Ditlevsen窄界限法的界限較窄，對比蒙特卡洛法，誤差在1%左右，可滿足工程精度需要，主次結合法計算結果也滿足工程精度要求；蒙特卡洛法需要計算多條失效路徑的聯合示性函數，在PC上得到一個結果需數天時間，效率較低。

3.3 基于模糊失效概率界限比的模糊可靠度分析

考慮隨機變量模糊隸屬函數為擬正態分布，失效準則模糊隸屬函數為對稱三角分布，以Rv代表隨機變量模糊性對界限比R的影響，Rz代表失效準則模糊性對R的影響。根據式(5)則有R=RvRz。

(1) 考慮R值與隸屬函數形式的模糊可靠度分析。首先，討論模糊隸屬度函數中參數k和α取值對模糊可靠度計算結果的影響。由于事件的模糊性隨隸屬函數參數k和α的增大而增強，則分別取兩個參數建議值的上界和下界組成四種邊界情況，即以k為0.5和3.0、α為0.01和1.00分別進行組合，得到不同隸屬度時的可靠指標區間如圖2所示。

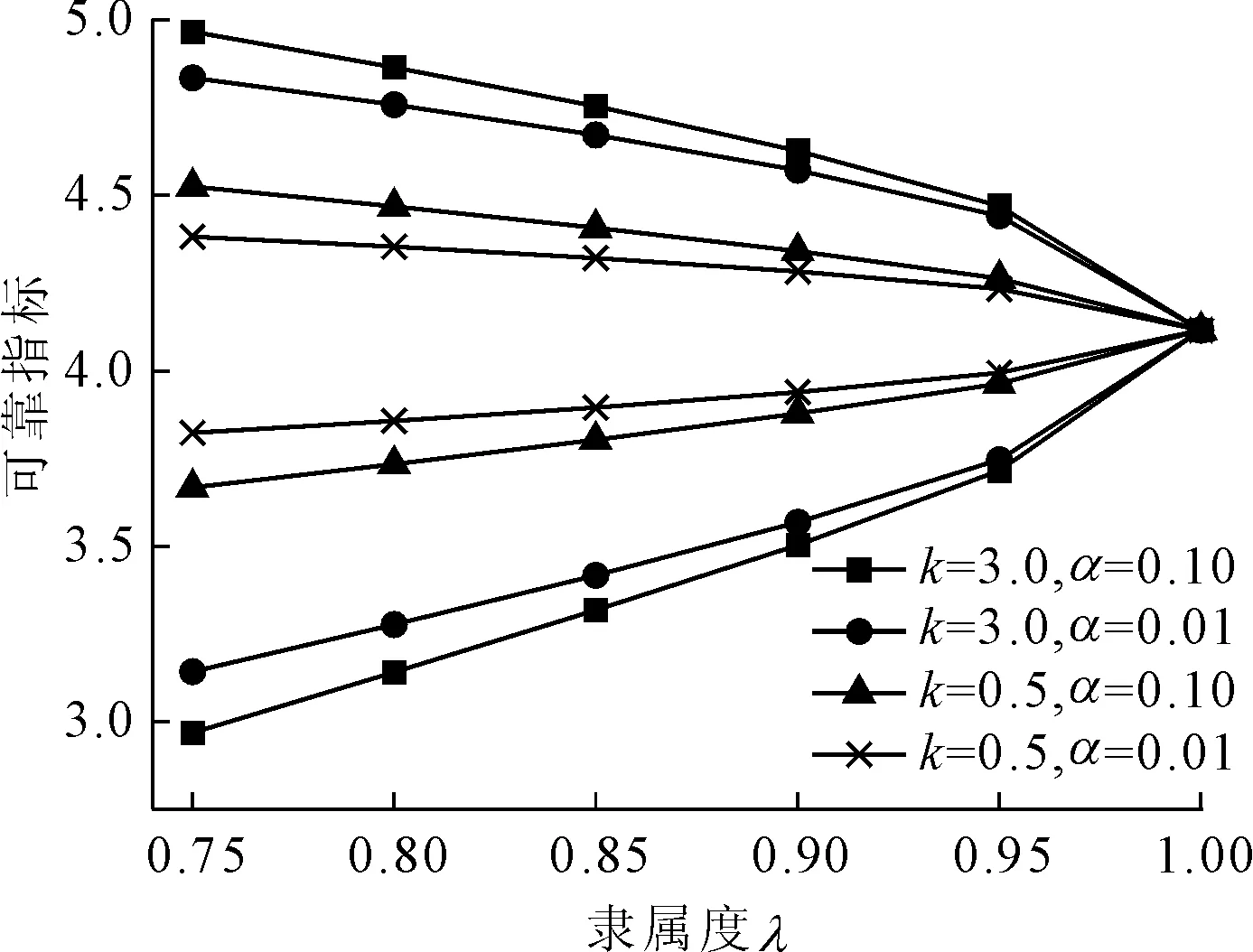
圖2 隸屬函數參數不同取值的可靠指標

從圖2可以看出，隸屬函數參數k和α的不同取值對模糊可靠指標區間范圍的影響較大，其中k值的變化對最終模糊可靠度范圍的影響相對顯著。

然后，考慮不同隸屬函數形式對模糊可靠度計算結果的影響。這里先假定當R值為定值且隸屬度為λ=0.75時不同形式隸屬函數的模糊性影響相同。當k=3.0，α=0.10時，本算例有Rv=1096.145，Rz=4.195。

以隨機變量隸屬函數為擬正態分布、三角分布，失效準則為正態分布、三角分布為例，對比不同隸屬函數形式的模糊可靠度計算結果，得到不同隸屬度形式組合時的可靠指標分布如圖3所示。圖中“擬正態-三角”表示隨機變量隸屬函數為擬正態分布，失效準則隸屬函數為三角分布，其余以此類推。

圖3 同R值下不同隸屬函數的可靠指標

從圖中可以看出，隸屬函數的離散程度直接影響到了模糊可靠指標區間的離散程度，且隨機變量模糊隸屬函數變化引起的結果改變更明顯，這是因為Rv遠大于Rz。以給定R值討論工程的模糊性時能得到關于隸屬函數形式對可靠度計算結果的影響的更定性的結論。

(2) 基于R值的加權平均法。如若要使用加權平均法計算模糊可靠指標綜合值，則失效概率的上、下界應在一個量級上以保證加權計算的合理性，即有R≤10。

以滑移通道EFGB(失效模式1)且不考慮隨機變量相關性以為例，取R=9進行試算。

分析其中Rv=Rz=3的情形，經過試算得到相應的k=0.237，a=0.0766，計算此時不同隸屬度的可靠指標，如表4所示。

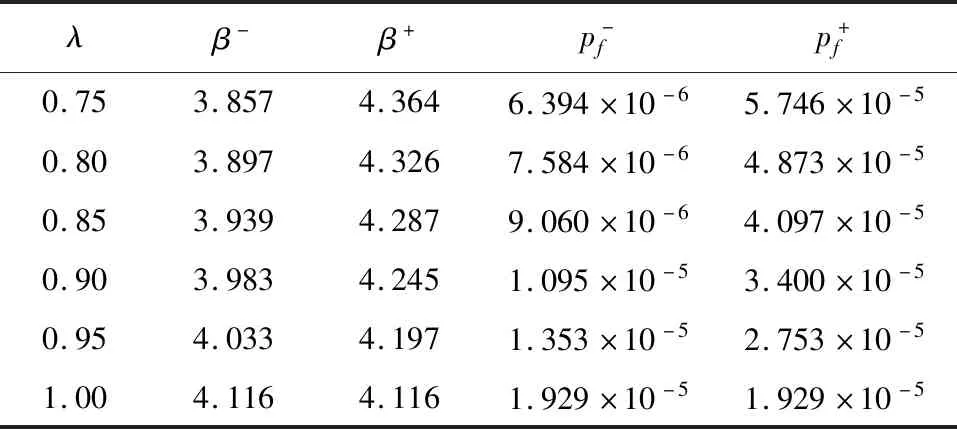
表4 模糊可靠度計算結果

對表4中失效概率加權求和，得到滑移通道EFGB的失效概率為2.457×10-5，模糊可靠指標為4.060，不考慮模糊性的結果為4.116，可見，不考慮模糊不確定性時可靠性計算結果偏于保守。

討論本算例中隨機變量模糊性和失效準則模糊性占R的比重，即Rvz的對模糊可靠地的影響，分別令Rvz為1/9和9，得到模糊可靠指標結果為4.070和4.048。Rvz從1/9增大到9時，結構的模糊性從完全由失效準則模糊性來決定過渡到完全隨機變量模糊性來決定，模糊可靠指標僅減小0.5%左右，影響非常小。

若R=9且完全由失效準則決定，對其取正態隸屬函數、三角隸屬函數、尖Γ隸屬函數，分別得到模糊可靠指標為4.004，4.057，4.072，變化并不明顯，從圖3可以推測，其值變化應該和隸屬函數在隸屬度范圍內的離散程度有關。

通過上面的分析可以知道，影響模糊可靠指標的因素主要來自于R值的大小以及隸屬函數的形式；而使用加權平均法后，由于同時需要對R值做假定，減小了隸屬函數形式的影響。

3.4 考慮模糊性的體系可靠度計算

從兼顧精度和效率上考慮，本文使用窄界限法求解模糊體系可靠度。另外，考慮如下代表性情況：對于隸屬函數的形式，隨機變量的模糊采用擬正態隸屬函數，失效準則的模糊采用對稱三角隸屬函數；對于模糊隸屬函數中參數的取值，考慮邊坡常用中k=3，α=0.1和k=0.5，a=0.01的兩種常規情況，以及假定R=9(Rvz=1)時不同滑移通道對應不同的k和α的情況。

通過模糊可靠度計算，得到單一失效模式不同隸屬度時模糊可靠度區間的上、下界值，然后采用式(6)進行體系可靠度計算，從而得到本工程的模糊體系可靠度的界限，計算結果如圖4所示。

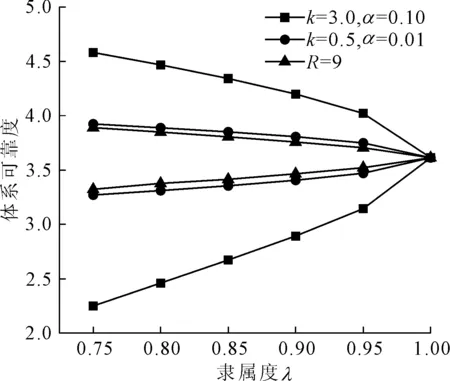
圖4 不同隸屬度的體系可靠指標

可見，當k=3.0，α=0.10時，得到的模糊體系可靠度區間很大。實際上當隸屬度為0.75時，使用邊坡工程中選取的模糊隸屬函數參數的取值，計算得到的模糊體系可靠度范圍為2.250～4.582，其界限比R最大達到5 301倍，使用加權平均法意義已經不大，只能作為一個粗略的參考。

借助加權平均法，計算R=9時不同ρf′c′對應不同的模糊體系可靠度，并和不考慮模糊性時的體系可靠度作為對比，由于本算例中窄界限法的區間上、下界差距不大，以其下界表示計算結果，并繪制不同隸屬度時的模糊體系可靠度值，計算結果如圖5所示。

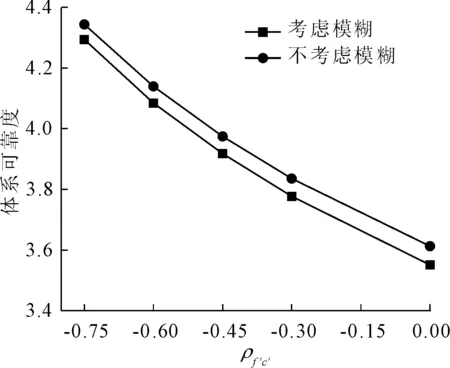
圖5 不同ρf′c′的模糊體系可靠度

可以看出，體系可靠度隨著隨機變量負相關性的增大而增大；考慮模糊時的體系可靠度值比不考慮模糊時要小，具有一定的借鑒意義。

4 結 論

本文結合模糊數學與體系可靠度理論，研究了重力壩多斜面多滑移通道壩基的抗滑穩定可靠度問題，結論如下：

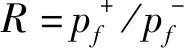
(2) 若使用加權平均法，影響模糊可靠指標的主要因素是R值以及隸屬函數形式，不過在規定R值的范圍內，隸屬函數形式的影響不大；本文工程實例對隨機變量使用擬正態隸屬函數時，R值隨k值變化很明顯，故k需要結合具體工程進行論證和選取。

(3) 窄界限法如果使用在失效概率較小的重力壩工程中，其界限很窄，參照蒙特卡洛法計算結果，其精度能滿足要求；重力壩抗滑穩定問題同時考慮整體體系和模糊性后，得到的可靠指標相對較小，在協調工程安全和工程建設的經濟性方面具有現實意義。