基于物聯網離散模型的能效關鍵指標預測*

潘 琛，楊瑞麗

（商丘工學院信息與電子工程學院，河南商丘476000）

1 引言

物聯網是在計算機互聯網的基礎上，利用RFID、無線數據通信等技術，構造一個覆蓋世界上萬事萬物的“Internet of Things”[1]。物聯網在制造業中有廣泛應用，尤其是在產品智能化、生產過程監控與管理，智能制造及智能物流等幾個方面，而離散制造業是我國制造業的重要組成部分，離散制造系統的能效評價對于構建綠色制造，實現科學發展觀具有十分重要的現實意義。目前我國離散制造系統存在自動化程度低、涵蓋范圍小、能效優化差等問題，導致離散制造業進行能效綜合評價是亟待解決的問題[2-3]。離散制造業伴隨著各技術領域的發展，也逐漸進入信息化的時代，其中離散制造系統能效分析和能效優化模塊是信息化過程中非常重要的環節。

離散制造系統中能耗部門比較多，會涉及多個層次，對離散制造業生產車間進行能效評價，可以綜合全面的體現其具體能耗水平。另外，離散制造系統的能效預測也是節能任務中非常關鍵的一個環節，我國也制定了企業加工設備能效評價和生產環境評價的標準，將來會率先對用能水平落后的加工設備進行逐步的淘汰。因此，對設備進行能效預測是十分有必要的。

2 能耗集成化數學模型

離散制造系統制造車間消耗的能量大都集中在產品加工的過程中，因此生產加工的能耗是其最主要的一個環節。離散制造系統制造車間的加工過程如圖1所示，其中不同的生產任務有不同的加工工序，一個加工過程會有多個設備共同完成，生產加工過程中會通過多個工序與設備來適配。

離散制造系統中，不一樣的加工工序、生產調度計劃、加工設備等都會使得作業車間的能耗改變。離散制造系統層的能耗主要分為三個層次：設備層、任務層和輔助生產層，它的能耗模型如圖2所示。以單位產品的一個制造過程為一個周期，先假設整個產品制造過程有n個流程任務，不同的工序共有m個加工設備進行完成，并且輔助的生產系統有M個輔助能耗系統去組成。

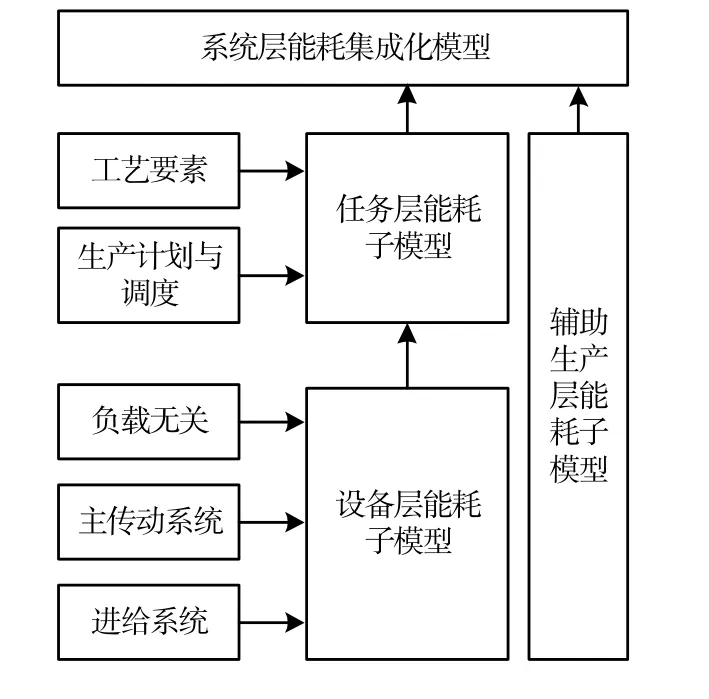
圖2 離散制造系統能耗模型圖

2.1 設備層能耗子模型

在離散制造系統中，加工設備的能源消耗主要用于主軸和伺服電機的運轉，其余消耗的能量主要用于輔助生產運行的設備等，文獻[3]強調了主傳動加工設備和伺服電機的能耗占大部分加工車間的能耗。以下從負載無關模型、主傳動模型和進給系統三個方面來介紹能耗子模型：

1)負載無關能耗模型

制冷設備、液壓設備和切削油泵等輔助性的設備都是負載無關消耗的能耗，所占能耗比重較小，負載無關的能耗受到輔助運行設備的運行時間和功率的影響，其能耗表達式為：

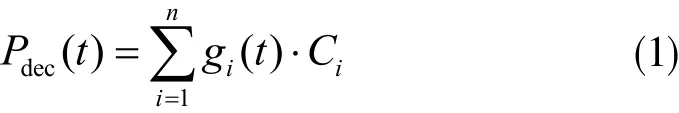
式中Pdec表示負載無關的總能耗，Ci表示第i個負載無關設備的功率值，可當作不變值。其中設備的運行狀態用gi來表示，在運行時為1，在空閑為0時，其能耗表達式為：

2)主傳動系統能耗模型

加工過程中主傳動系統的能耗是最主要的設備能耗。能耗主要有變頻器、電機損耗和機械傳動摩擦損耗三個來源，在整個加工過程中，輸入功率Psp在將能量輸出到切削加工區域去實行加工任務之前，需要經過上述的三個損耗來源，其能耗表達式為：

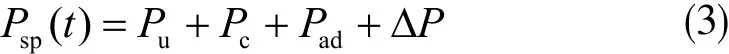
式中ΔP為變頻器損耗，Pu為空載功率，Pc為切削功率，Pad為附加載荷損耗。

3)進給系統能耗模型

每個零件的加工過程中需要經歷不同的刀具以及不同的設備來執行配合，刀具和設備的動力源自于加工系統中的進給子系統，進給系統的能耗與加工任務有著很大的關聯性，其具體表達式為：

式中Paxu為進給系統的輸出功率，Paxc為進給系統的空載功率。

2.2 任務層能耗子模型

在離散制造系統任務層中，研究任務層的能量消耗對于整個作業車間的能量消耗舉足輕重。加工訂單中包含了多個生產要素，如加工工藝路線、加工工藝參數等，這些生產要素都會引起生產過程中任務層的能耗差異。以下從生產工藝要素、生產計劃和調度方案來敘述任務層的能耗子模型。

1)工藝要素的能耗模型

先建立工藝要素與切削能耗之間的模型，將加工任務i的某一工序Pik作為其節點，假設Mik表示當前生產加工任務中的機械設備，其中{θ1,θ2,...,θi}表示為加工任務中的加工運行參數，{O1,O2,...,Oi}為具體加工工藝路線，具體工藝要素能耗模型為：

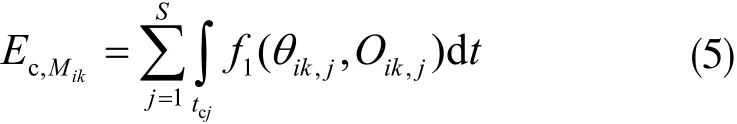
其中i為加工任務，k表示工序數，j是工序的工步數。

2)生產計劃與調度能耗模型

在生產過程中，設備空載時間的差異會影響設備的能耗。設備空載表達式為：

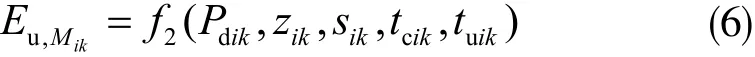
其中Pdik表示第k臺設備的空載額定功率，sik表示加工批次的大小，加工任務個數用zik來表示，tcik表示第k臺機床加工第i道工序的標準時間，第k臺機床上空載時間是會受到影響的變量，用tuik來表示。由上所得，離散制造任務層的能量模型Etask的表達式為：

2.3 輔助生產層的能耗子模型

離散制造系統中，輔助生產層的能耗任然存在，進行生產能耗的量化分析也應該將其考慮進去。設M個輔助生產能耗子系統組成輔助生產系統，在相同的時間內，如果輔助生產條件不變的化，那么輔助生產設備的能耗將不會明顯變化，可以幫他當作常數。輔助生產層的能耗自模型為：

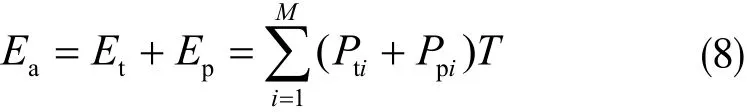
式中Ea表示整個輔助生產層的能耗，零部件之間的運輸設備總能耗用Et來表示，Pti表示零部件在運輸時運輸設備的額定功率，Ep表示輔助生產層里面所有設備消耗的能耗，Ppi表示輔助生產層里面所有生產設備的具體額定功率，T為給定加工區間內各設備運行的時間。

從離散制造系統層能耗集成化模型可知實時變化設備能耗是能耗之本，而其直接獲取有效加工效率則非常困難。加裝傳感器價格昂貴。并且影響生產精度，故在此提出一種能效關鍵指標辨識方法，用于預測加工效率。

2.4 設備層能效及有效功率預測模型

以機床加工為例，設備主要是指生產車間的加工機床，機床在加工零件時會在機床照明、材料切除能量等方面存在消耗。而真正有效的能量是材料切除能量。設備層能量效率可以定義為輸出功率與輸入功率的比值[4]，設備層的能效則為切削功率與輸出功率之比值，即：

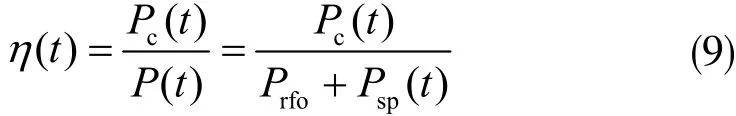
其中P(t)表示輸入功率，Pc(t)表示切削的功率，Prfo表示固定能耗，Psp(t)表示機床加工時的輸入功率。

由式(9)可以看出，此效率表示機床的瞬時效率。對機床來說，這只是瞬態能量效率。企業則重視某一加工時段T或是完工某一工序時該機床的能量效率，因此設備層能效應可以定義為機床有效的用于材料切除的能量Ec和機床消耗的總能量E的比值，即:

其中tb是開始時間，te是結束時間。削功率Pc(t)可以通過直接安裝力傳感器來采集，但是這樣的做法會引起加工機床在加工時轉向不精確等問題。針對此問題，此處提出變遺忘因子算法，用來估計附加載荷損耗系數，進而以此為基礎估計出切削功率。

加工機床的輸入功率主要分為三大部分：Pu(t)，Pc(t)和Pad(t)，它們之間的關系如下式：

式中Pu(t)指加工機床的空載功率，Pad(t)指加工機床的運行負載損耗。

附加載荷損害是有電機損耗、機械損耗和電能損耗組成的，并且附加載荷損耗是切削能耗的二次函數[5]，具體為：

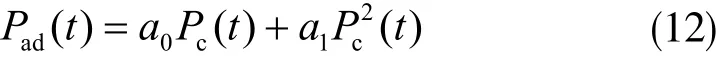
其中a0和a1是附加載荷損耗系數。

從式(11)和(12)可以得出:

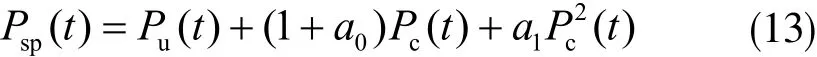
式(13)可進一步轉換以求出切削功率，其式為：

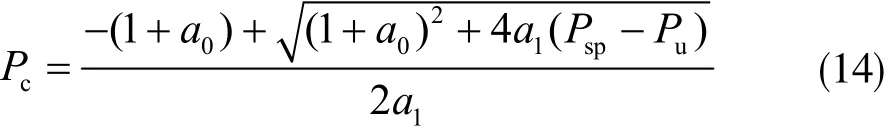
其中Psp和Pu可以通過智能電表和功率傳感器獲取，但a0和a1不能通過測量來取得，此處采取變遺忘因子算法來估計其附加載荷損耗系數。

3 基礎加工數據的獲取

由式(14)的預測模型可以看出，要求取切削功率，需要知道加工機床的Prfo、Pu和Psp等數據。

加工機床固定能耗Prfo的獲取，是在機床完全準備好的情況下，主機、外設單元驅動器機床控制器和其電機開啟，但其加工機床主軸與進給電機并沒有運動時的功率值。在離線非加工狀態下獲取機床功率值，放入數據庫中。

空載功率Pu是在測量不同加工轉速下的加工機床空載功率，記錄在基礎數據庫中。

主軸的輸入功率Psp通過功率傳感器測量，并將得到的輸入功率放入數據庫中。

所提出的變遺忘因子遞推辨識算法解決了載荷損耗系數的獲取困難的問題。使用西門子機床提供的OEM軟件來采集加工機床的基本能耗數據，計算出加工機床的切削功率[5]，其中載荷損耗系數的辨識是采用變遺忘因子遞推辨識算法估算求出的，最后按照能效模型式(14)求取機床的切削功率。獲取系數的框架如圖3所示。

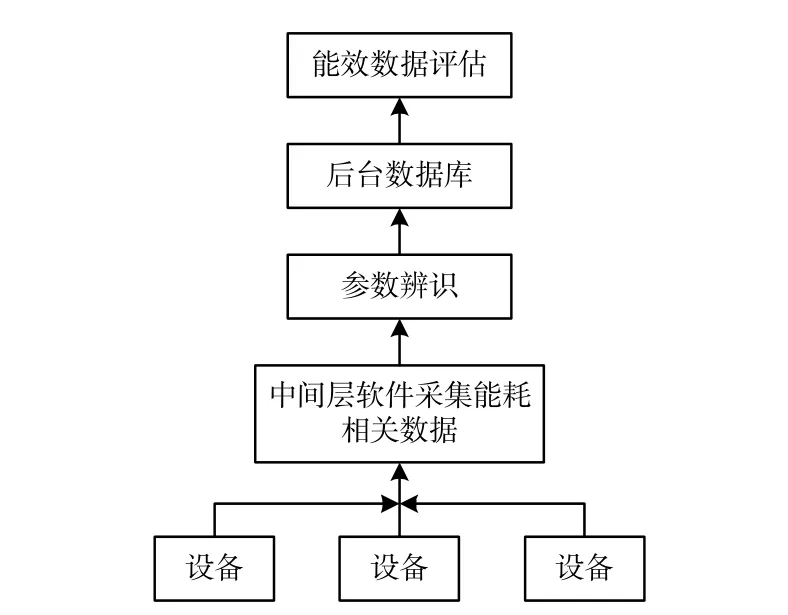
圖3 基礎數據/參數獲取框架

4 基于變遺忘因子的參數辨識方法

最小二乘算法是高斯在研究星體運動軌道的預報研究工作中提出來的，它是估計理論的基石。但是隨著數據增長，算法中的協方差矩陣P(k)將趨于零，致使最小二乘算法逐步出現數據飽和的情況。變遺忘因子辨識算法就是為了克服這一類數據現象從而提出辨識算法，它的基本思想就是對舊數據加入變遺忘因子，增加新數據在協方差矩陣P(k)中的占有量。

變遺忘因子法采用下列辨識模型：

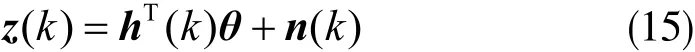
其中：

z(k)表示系統輸出，h(k)表示可以觀測的數據向量，n(k)表示系統噪聲。

取k=1,2,...,L。L表示數據的長度。公式(15)可變換為線性方程組：

其中：

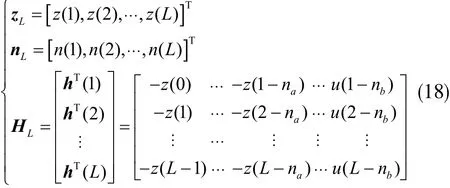
取準則函數為：

式中μ為遺忘因子，其取值范圍為0＜μ＜1。遺忘因子的作用是提升新數據在協方差矩陣P(k)中的信息量。當k=1時，衰減率是μL-1；當k=L時，衰減率為1，即是說，當前的數據是不衰減的。

將公式(19)寫成寫成二次型：

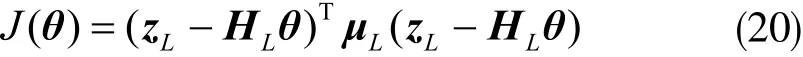
其中HLθ為系統模型輸出，J(θ)時用來比較模型系統輸出和系統模型輸出的相近度。通過把準則函數J(θ)極小化，然后獲取系統模型的估計參數θ?，從而使模型輸出更加逼近實際值。

K時刻參數的估計值為：

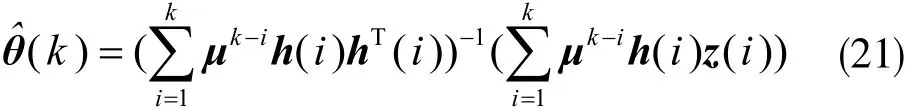
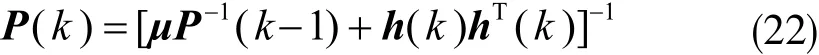
令K(k)=P(k)h(k)，則可以推導出如下的基于變遺忘因子遞推辨識算法：

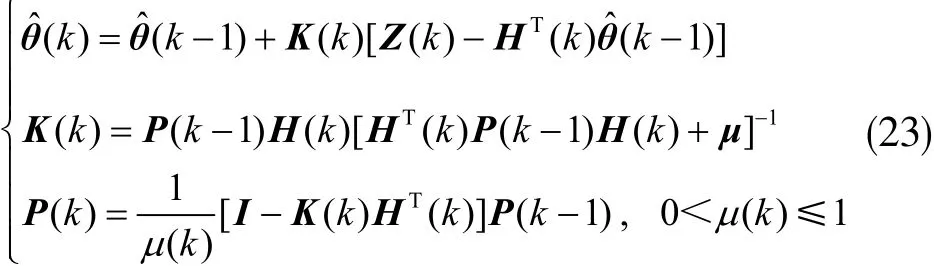
協方差矩陣P(k)的在辨識算法中積累辨識數據的信息總量，但是隨著辨識不斷進行，新數據不斷產生，舊數據在P(k)中也越積越多，當達到某個程度，舊數據會將P(k)填滿，使其趨于飽和，最小二乘法最終會出現辨識結果準確度不高的問題[6]。通過引入遺忘因子，即是為了降低舊數據的占有量。

5 設備能耗關鍵參數的辨識

使用變遺忘因子算法來求取加工機床加工時的載荷損耗系數。首先采集加工設備在一定主軸轉速下的Pu(t)，然后制定在相同轉速下不同切削量的多個加工方案，測取多組Psp(t)與Pu值，按照式(13)得到如下的含l個方程的方程組：

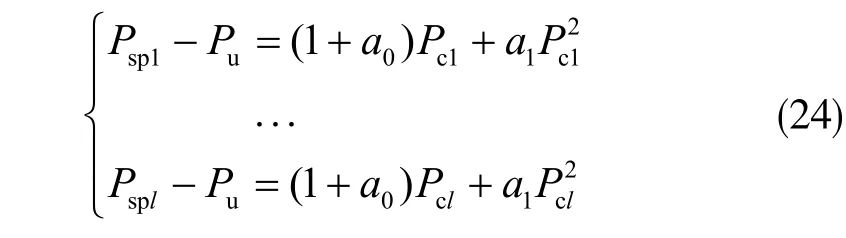
式(24)整理成矩陣形式，具體為:

經過變遺忘因子遞推辨識算法估算出載荷損耗系數，具體見式(23)。

變遺忘因子μ(k)=μ0μ(k-1)+(1-μ0)，式中μ0=0.99，μ(0)=0.95。μ的取值對算法的性能有直接影響，μ值增大，算法的魯棒性增強，但跟蹤能力下降；μ值減小，算法的魯棒性下降，跟蹤能量增強，對干擾更為敏感[7]。μ在通常情況下的取值范圍為0.95～0.99。

在獲得了Psp、Pu與a0、a1后，就可以根據公式(14)來預測出t時刻的切削功率Pc(t)。然后根據智能電表求取公式(9)分母中的和固定能耗Prfo，此時即可求取離散制造系統的能量效率η(t)。

在加工機床的切削參數一樣前提下，通過實驗驗證，結果表明其估計誤差在±5%以內，然而文獻[8]傳統的方法其誤差在10%以上，因此，本算法更加接近真實值。

6 結束語

在物聯網的多智時代，如何改善制造業的能效評價體系一直是研究學者所關注的重點。離散制造能效評價中，關鍵難點是車間生產現場的設備能效的有效獲取。針對設備層能效直接獲取困難，提出了基于參數辨識的設備能耗預測方法，利用測量獲取的設備總功率和主軸實時功率，采用基于變遺忘因子遞推辨識算法來估計設備加工能耗模型中的關鍵參數，基于能耗集成化模型預測出有效加工功率，最終可以求取其能效。實驗表明，通過有效獲取加工設備參數，所提算法很大程度上改善了生產能效，為企業進行能效優化提供了重要參考。