一類復雜通信條件下高階線性群系統編隊控制

石曉航，張慶杰，呂俊偉

（1.海軍大連艦艇學院，大連116001； 2.空軍航空大學，長春130022； 3.海軍航空大學，煙臺264001）

群系統編隊控制在很多領域都有著廣泛的應用，比如監視和偵察［1-3］、目標搜索和定位［4-7］、中繼通信［8］以及空間探索和資源探測［9-10］等。傳統的編隊控制方法主要包括：領導者-跟隨者［11-12］、行為方法［13］以及虛擬結構［14］。但從應用情況來看，這3種方法依然存在著魯棒性差、行為建模復雜和通信量大等方面的不足。隨著多智能體一致性理論的發展，越來越多的學者開始研究基于一致性算法的分布式編隊控制方法［15-16］。文獻［15］指出，上述3種傳統方法均可看作是一致性算法的特例。

基于一致性協議，文獻［17-18］討論了輪式小車的編隊控制問題。文獻［19］提出了大規模一階群系統有限時間編隊框架。基于一致性線性化反饋方法，文獻［20］研究了無領導者方式的多無人機編隊控制問題。進一步，文獻［21］研究了多無人機時變編隊控制的分析和設計問題，并給出了編隊形成的充要條件。文獻［15，17-21］的研究對象 主 要 是 低 階 群 系 統，比 如 一 階［17-19］、二階［15，20-21］。假 定 網 絡 通 信 拓 撲 為 無 向 圖，文獻［22］分析了一類由多個二階系統串聯組成的高階群系統編隊控制問題。對于有向通信拓撲結構，由于其Lap lacian矩陣的特征值可能存在復數，判斷編隊形成具有一定難度。文獻［23］利用狀態／輸出反饋，研究了有向通信拓撲條件下的編隊形成問題。

上述文獻均假設理想網絡通信條件，但在實際的應用中，受到周圍環境或其他因素的影響，可能出現通信時延、拓撲不確定以及外部擾動等情況。文獻［24］通過引入自身時延，給出了二階群系統實現時不變／時變編隊的充分條件。文獻［25］討論了同時存在位置時延和速度時延條件下的一致性策略和編隊控制穩定性。文獻［26］采用頻域方法，借助Nyquist穩定性判據給出了編隊穩定的時延相關／非相關條件。文獻［24-26］均假定固定通信時延。對于時變時延，文獻［27］研究了某型垂直起降無人機的編隊控制方法。同時考慮時變時延和有向拓撲，文獻［28］設計了二階群系統編隊控制協議，同時討論了時變時延對編隊形成的影響。文獻［29］給出了含有時變時延高階群系統實現編隊的充要條件和編隊控制器的設計方法。文獻［30-31］采用Lyapunov穩定性理論分析了通信時延的邊界條件。文獻［32-33］研究了群系統模型存在范數有界不確定性情況下的編隊控制問題。利用魯棒控制理論，得到了群系統編隊控制穩定性條件。針對時延、拓撲不確定和外部擾動條件下的高階群系統編隊控制問題，目前的研究成果很少。文獻［34-35］只討論了控制器增益已知情況下的群系統魯棒一致性問題。

本文主要討論一類同時存在時變時延、拓撲不確定和外部擾動等復雜通信條件下的群系統編隊控制問題。與已有文獻相比，主要貢獻有：

1）高階線性群系統模型。文獻［17-21］所討論的群系統大都針對一階或二階積分器，而高階模型不具有一階、二階模型的特殊結構，因此文獻［17-21］方法不適于高階線性群系統。本文方法具有更廣泛的應用范圍。

2）同時考慮時變時延、拓撲不確定及外部擾動等3種通信條件。目前針對復雜通信條件的編隊控制問題研究較少，僅有文獻［34-35］討論了3種通信條件同時存在的群系統一致性可行性問題，且沒有給出控制器增益的求解方法。

3）低保守性。文獻在分析編隊所允許的最大時延上界時采用了Lyapunov穩定性方法，所得結果是充分條件，具有一定的保守性。不同于文獻［30-31］方法，本文將自由權矩陣引入分析過程中，使所得結果具有較低的保守性。

本文首先簡要介紹了圖論知識和相關引理；并建立了一類復雜通信條件下高階線性群系統編隊問題的數學描述，同時設計了基于一致性算法的編隊控制協議。然后給出了群系統實現編隊的充要條件，利用Lyapunov-Krasovskii泛函分析方法得到群系統編隊所允許的最大時延上界和控制器增益求解方法。最后利用數值仿真實驗，對所提出方法的有效性進行驗證。

1 圖論知識及相關引理

1.1 圖論知識

1.2 相關引理

引理1［36］圖G的Laplacian矩陣L至少有一個0特征值，且向量1是0特征值所對應的右特征向量，即L1＝0。如果圖G是一個有向圖，且含有一個有向生成樹（至少存在一個節點到其他所有節點都有一條有向路徑），則0是L的單特征值，其余的非零特征值均具有正實部。

引理2［37］如果矩陣Y∈RN×N的各行和均為 零，則 存 在 矩 陣 Z∈RN×（N－1）和 矩 陣 E∈R（N－1）×N使得Y＝ZE，E的定義為

如果0是矩陣Y的單特征值，那么矩陣Z是列滿秩的。

引理5［40］給定具有適當維數的矩陣Q ＝QT、H和E，則Q＋HF（t）E＋ETFT（t）HT＜0，對所有滿足FT（t）F（t）≤I都成立的充要條件是存在一正數ε＞0使得Q ＋ε－1HHT＋εETE ＜0成立。

引理6［41］對矩陣X∈Rm×n和矩陣Y∈Rn×m（n≥m），二者乘積滿足如下性質：①若λ是矩陣XY的特征值，則λ也是矩陣YX的特征值。②若λ≠0是矩陣YX的特征值，則λ也是矩陣XY的特征值。③若λ1，λ2，…，λm是矩陣XY的特征值，則矩陣YX的n個特征值為λ1，λ2，…，λm，0，…，0。

2 問題描述

2.1 高階線性群系統模型

2.2 編隊控制協議

3 主要結果

3.1 編隊形成的充要條件

針對高階線性群系統的編隊形成問題，本文主要考慮如下3種通信約束。

假設1 時變時延dt滿足：

式中：ˉdt和μ為常數，且0＜μ＜1。

假設2 拓撲不確定性。若用鄰接矩陣的變化量ΔW ＝［Δwij］∈RN×N來描述通信拓撲不確定性，則有

式中：矩陣E的定義由引理2給出。

由引理1、引理2可知，存在列滿秩矩陣Z∈RN×（N－1）及ΔZ∈RN×（N－1），使 得L＝ZE，ΔL＝ΔZE，對式（12）求導得到

考慮J和ΔJ的結構，閉環系統（16）等價于定理1的條件3中的N－1個閉環子系統，其中λi（i＝1，2，…，N－1）表示矩陣EZ的特征值，由引理1和引理6可知，矩陣EZ的特征值與矩陣L的非零特征值相同，因此λi（i＝1，2，…，N－1）也是矩陣L的N－1個非零特征值。由上述推導可知條件3也是必要的。

充分性 因為矩陣B是列滿秩矩陣，由引言可知，存在一個非奇異矩陣～B＝［～BT1，～BT2］T，滿足～B1B＝I且～B2B＝0。

如果條件1和條件2成立，則有

3.2 K2的設計

定理2 考慮復雜條件（4）、（5）和（6），若存在適當維數的實矩陣ˉP＝ˉPT＞0，ˉQ＝ˉQT≥0，ˉR＝ˉRT＞0，ˉV以及常數a和b（b≠0），ε＞0，使得下式成立：

接下來將分別討論?⌒（t）≠0和?⌒（t）＝0兩種情況。

由引理4可知，式（27）與式（28）同時成立，當且僅當

根據引理3，式（30）等價于

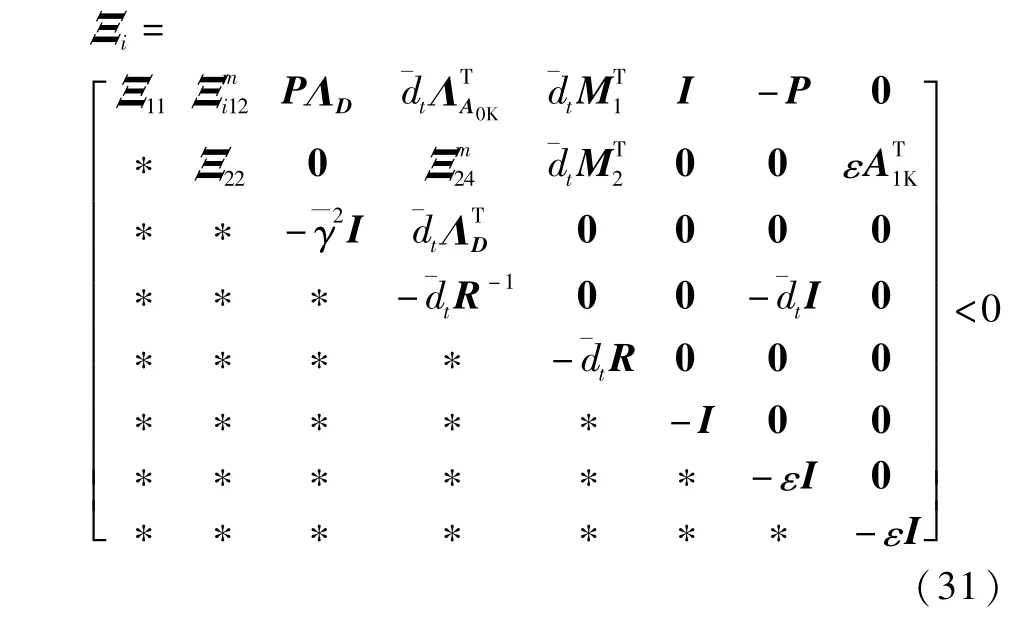
通過上述整理可知，如果不等式（31）成立，則不等式（26）成立，即閉環系統（10）在非零的?i（t）擾動條件下，具有給定的H∞性能指標γ。

基于上述的討論，可以利用如下的算法對編隊控制協議（2）進行設計，使群系統（1）在時變時延、通信拓撲不確定和外部擾動條件下，滿足給定的H∞性能指標。

算法1 對于群系統（1）和編隊控制協議（2），控制器增益K1和K2，以及輔助函數vi（t）（i＝1，2，…，N）的設計可以參照如下步驟：

步驟1 判斷定理1的條件1中式（8）是否成立，若成立，則通過條件2的式（9）求解出編隊輔助函數vi（t）。

步驟2 選取適當的控制器增益K1，令A＋BK1的特征值在復平面上的指定位置，完成對編隊中心運動模態c（t）的配置。

步驟3 根據定理2，可以求出a、b和時延上界ˉdt，進而得到控制器增益K2。同時，利用參數a和b，還可以得到不同時延下對應的控制器增益K2。

4 數值仿真

假設1個群系統由8個主體組成，各個主體之間的通信拓撲G如圖1所示。

圖1 通信拓撲GFig.1 Communication topology G

形成編隊之后，8個主體會分布在一個橢圓形的圓周上，組成一個八邊形并圍繞橢圓的圓心旋轉。

利用算法1中的步驟1，可以求解出編隊輔助函數為

選取K1＝［5.75，－8.5，－8］將A＋BK1的極點配置在－2、－1＋i和－1－i。這時，編隊參考c（t）是靜止的。設定γ＝1.4，利用算法步驟3，得到時變時延上界為ˉdt＝1.7 s。選取時變時延為dt＝1.2＋0.5sin t s，此時，得到的控制器增益為

K2＝［－0.016 4，0.0141，0.0084］。

各主體的初始狀態分別為：xi1（0）＝4（δ－0.5），

xi2（0）＝3（δ－0.5），xi3（0）＝2（δ－0.5）（i＝1，

2，…，8），其中δ為（0，1）之間的隨機數。通信拓撲的不確定性為ΔL＝0.9sin t L，外部擾動ωi（t）取［－2，2］之間的隨機數。仿真時間為50 s，假設通信拓撲的不確定性始終存在，并在25～27 s加入外部擾動。圖2（a）～（f）給出了8個主體的狀態和c（t）的狀態在不同時刻的截圖，以及8個主體的編隊構型。從圖中可以看出，本文設計的編隊控制協議可以使群系統在具有時變時延、通信拓撲不確定和外部擾動的條件下形成時變編隊。在出現外部擾動時，8個主體的隊形受到了一定的影響，但擾動消失之后仍能重新形成指定的時變編隊并保持穩定。圖3（a）～（c）分別給出了各主體的3個狀態與編隊相應狀態差值的曲線，各主體3個狀態與參考編隊相應狀態分量的差值曲線逐漸減小并趨于一致，在外部擾動出現之后，各主體的誤差一致性受到了一定的影響，但各主體能迅速地調整各自狀態并恢復指定的編隊。從仿真結果可以看出，本文的控制方法具有抗擾動的性能，可以有效地抑制時變時延、通信拓撲不確定及外部擾動對群系統編隊形成產生的影響，能保證群系統形成時變編隊并保持隊形穩定。

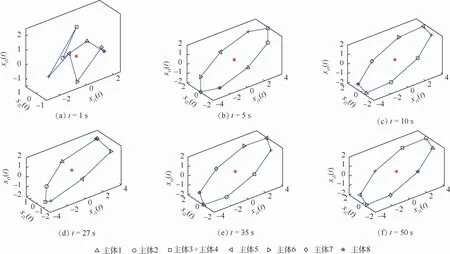
圖2 8個主體的狀態和c（t）的狀態在不同時刻的截圖Fig.2 Snapshot of states of eight agents and c（t）at differentmoments

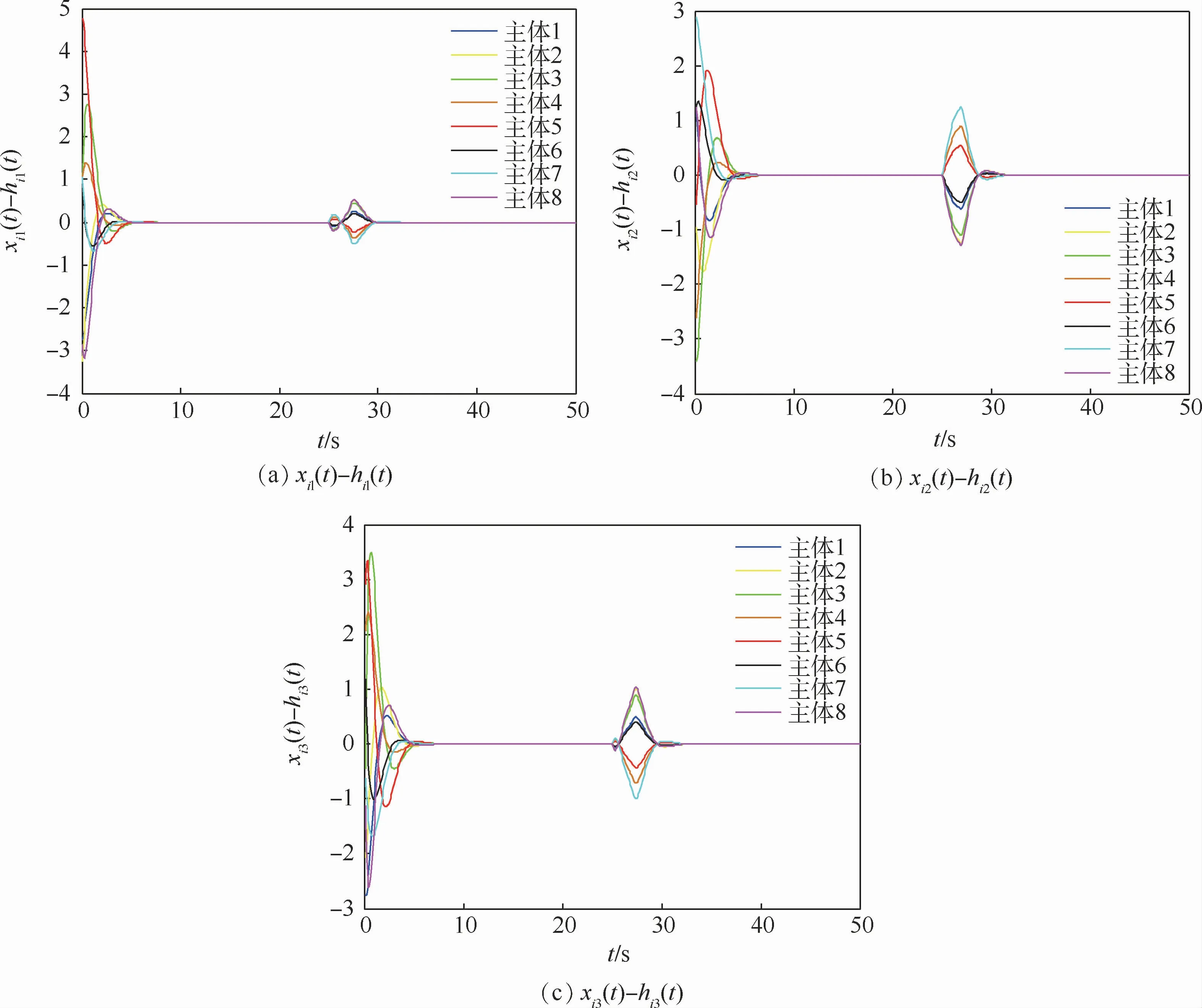
圖3 主體與編隊的狀態差值曲線Fig.3 State curves of differences between agents and formation

圖4 8個主體的性能指標曲線Fig.4 Performance index curves of eight agents

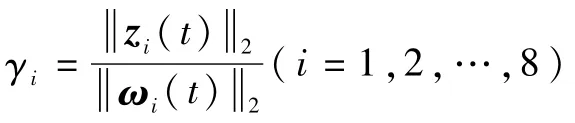
5 結 論

本文討論存在時變時延、通信拓撲不確定和外部擾動的高階線性群系統編隊控制問題，具體結論如下：

1）給出了群系統在給定的H∞性能指標下，實現編隊H∞控制的充要條件。

2）采用變量代換，將群系統的編隊控制問題，轉化為具有外部擾動時延系統的H∞控制問題。通過構造公共Lyapunov-Krasovskii泛函，討論了具有外部擾動時延系統的H∞控制問題，得到了保守性較小的LMI判據，利用數值計算方法，可得到群系統允許的時延上界。