腐蝕混凝土管道氣液兩相流非線性有限元分析

張 倩，何文社

(蘭州交通大學 土木工程學院，甘肅 蘭州 730070)

混凝土已經成為工程建設中不可多得的材料，相較于其他材料具有力學性質較穩定、價格便宜、耐久性能好等優點。因此，市政地下排水管網也多以混凝土管道為材料。截止2016年我國已建成的排水管道總里程達到50多萬km，因此，混凝土地下管網被喻為城市的“地下生命線”，對城市的正常運行起著關鍵性的作用[1]。然而排水管道中由于存在酸性物、堿性物、硫化物、游離的二氧化物以及可能存在的鉀、鈉、鎂、鐵離子和二氧化碳等會破壞混凝土結構的完整性，使混凝土的力學性能降低，造成管道滲漏破壞從而使路面塌陷等，嚴重影響人民生活以及城市的生態環境[2]。

國內外學者對管道腐蝕機理和腐蝕對管道力學性能的影響已經做了大量的研究。1972年，Erickson[3]對污水環境下的混凝土管道進行了腐蝕機理研究，發現在管道底部淤積的雜物中存在硫酸根離子，會與硫離子產生還原反應生成硫化氫，而由于管壁會有細菌的存在，硫離子會與管壁上部空間的細菌產生生化反應生成硫酸，硫酸的腐蝕作用會造成混凝土管壁的破壞。Ye等[4]對特定情況下具有對稱缺陷的軸向均勻腐蝕管道進行了研究，考慮腐蝕后管道各個參數的變化，使用Phython腳本和Fortran子程序對腐蝕管道的參數進行研究，利用腐蝕管道參數研究成果模擬出了其在外部力作用下的失效壓力。

杜婕[5]利用ANSYS軟件對腐蝕直管進行了非線性有限元分析，分析了腐蝕長度和深度以及寬度對腐蝕管道力學影響，得出寬度的影響比深度和長度稍小，且管道內腐蝕影響規律和外腐蝕基本一致。王志委[6]采用多種方法對圓形混凝土管道的腐蝕規律及力學性能進行研究，對腐蝕后的混凝土管壁材料各項參數進行折減，利用ANSYS進行了數值模擬，所得結果與理論和試驗結果的規律基本一致。王直民[7]應用數值模擬對管道在恒定交通荷載和簡諧荷載下管道的縱向以及橫向受力特性進行了分析研究，得出車輛經過路面時管道的豎向位移也呈對稱分布，下部的位移值大于上部，最大值位于管道下端。羅懿[8]使用ANSYS Workbench軟件模擬了管道外部在不同形狀腐蝕缺陷下的管道力學特征，并通過分析得出不同腐蝕缺陷尺寸下管道的力學特征，并由此得出管道的失效壓力，結果表明，不論何種形狀管道外腐蝕缺陷，缺陷深度增加均會明顯降低失效壓力。鄭恒偉等[9]通過ANSYS軟件分析了管道在不同腐蝕尺寸缺陷下的極限承載能力，并通過實驗與模擬值進行對比，研究出不同腐蝕尺寸對管道等效應力的影響。梁莉等[10]研究了腐蝕作用對管道整體剛度及管土相對剛度的影響，采用管壁彈性模量折減法推導了受腐蝕埋地式混凝土管管周土壓力的計算公式。駱正山等[11]考慮管道油氣兩相流，以兩相流均勻腐蝕下的管道為研究對象，使用斷裂力學的基本原理，建立了管道剩余強度評價模型，由此可以判斷出腐蝕缺陷下管道可接受程度。 以上研究大多集中在對管道腐蝕機理和失效壓力的研究，且管道中的流體為單相流。本文主要針對腐蝕混凝土排水管道，以文獻[6]的實驗數據為基礎，模擬管道內壁的腐蝕狀況，考慮流固耦合、交通荷載以及土壓力對氣液兩相流腐蝕管道進行非線性有限元分析。

1 仿真分析

本文所建立的有限元模型包括6部分：管周土體，未腐蝕管道，腐蝕管道(包括承插接口)，管內流體，橡膠圈，交通荷載(見圖1)。

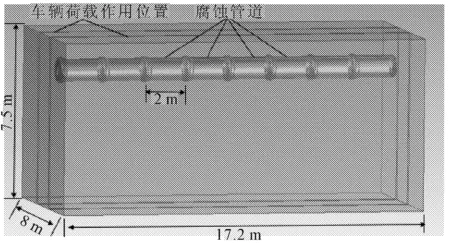
圖1 模型整體結構圖

1.1 結構模型

結構模型包括土體模型和管道模型，在Gambit軟件中建立模型并在ANSYS Workbench軟件mesh模塊中劃分網格，土體模型共34 567個單元，管道模型共21 453個單元，模型材料參數見表1，在土體四周約束其法線方向的自由度，在土體底面約束所有方向的自由度；依據規范《混凝土和鋼筋混凝土排水管》[12](GB/T 11836—2009)選取模型的管道尺寸，管道的內徑為800 mm，壁厚92 mm，土體的覆蓋深度為1 m,約束管道兩端所有方向的自由度。

本文采用參數折減法對管壁材料進行折減模擬管道腐蝕，以文獻[6]的實驗數據為基礎設置材料參數強度折減系數，以管壁相對腐蝕溶液濃度(C/C0) 65%為分界點，濃度大于65%時混凝土已經完全喪失力學性能，所以將強度折減系數定義為0；濃度為0時的混凝土力學性能良好，參數強度折減系數設置為1；中間按線性插值計算其材料參數強度折減系數，具體見下式。本文腐蝕管段為中間4節，管頂為腐蝕位置，以30°來表示腐蝕寬度，管壁方向產生的腐蝕影響深度設為27.6 mm，用強度折減系數確定的參數值來模擬管內壁至外壁腐蝕程度，并且依次遞減5層，每層厚度為5.52 mm，管道模型參數如表1所示，腐蝕管道區域如圖2所示，腐蝕管道折減區域參數如表2所示。

x=C/C0

(1)

(2)

E=kE0

(3)

式中：C為管壁某一點的腐蝕濃度；C0為管壁腐蝕濃度；x為管壁某一點處相對腐蝕濃度；k為材料參數強度折減系數；E為腐蝕后的混凝土彈性模量；E0為未腐蝕混凝土彈性模量。

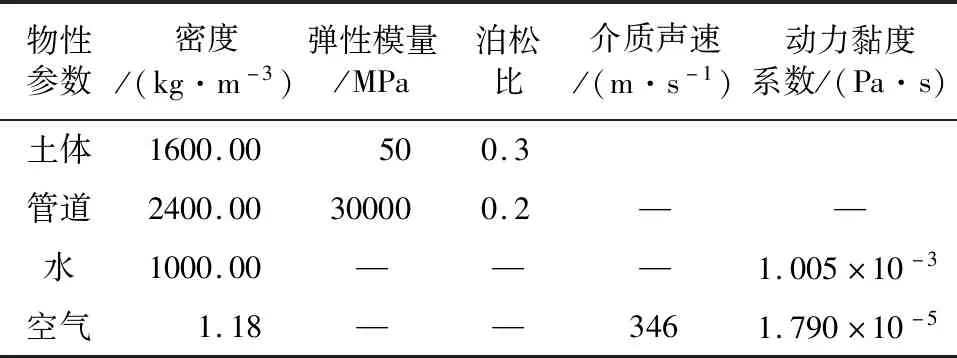
表1 材料參數

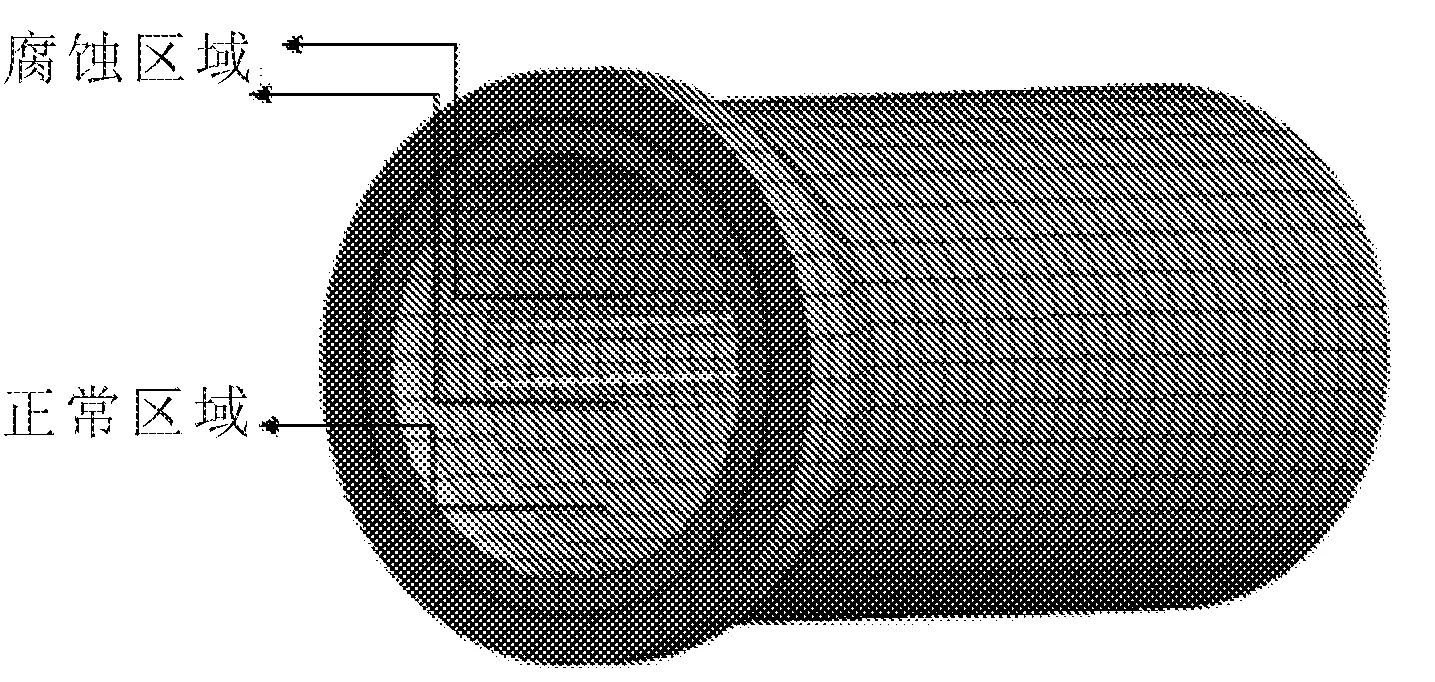
圖2 管道腐蝕區域圖

表2 腐蝕區域管道參數

1.2 橡膠圈模型

橡膠是一種超彈性材料，橡膠圈主要應用于承插接口，起到密封管道接口的作用， Mooney-Rivlin、Ogden三次式和Van Der Waals三個應變能函數能較好地擬合橡膠單軸和平面拉伸性能[13]。本文利用ANSYS Workbench軟件采用Mooney-Rivlin應變能函數來模擬橡膠圈，進行非線性有限元分析，具體見式(4)，相應參數如表3所示。

(4)

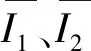
(5)

(6)

表3 Mooney-Rivlin應變能函數參數

1.3 載荷模型

管道結構設計中必須考慮的指標之一是交通荷載，是管道上方最頻繁的外荷載，其主要通過管道上方土壓力間接作用于管道。本文根據《給水排水工程管道結構設計規范》[14](GB 50332—2002)，將交通荷載簡化為簡諧荷載，輪壓0.7 MPa，車速40 km/h，交通荷載軌跡距管軸中心線1 m，車輛荷載作用區域為兩條矩形，寬0.193 m，長17.200 m。

1.4 流體模型

ANSYS Workbench軟件流體網格劃分對邊界層進行加密處理以更好的模擬壁面物理特性，本研究中流場計算域為管道的整個內部區域，使用FLUENT中的VOF(流體體積率法)模型模擬管道內氣體和液體的兩相流動。該模型適用于計算空氣和水這樣不能互相摻混的流體流動，同時采用Standardk-ε湍流模型[15]，各參數值如表1所示。

時間差分采用全隱式方案，時間步長取3 s，流體入口邊界條件為速度進口，進口流速v=5 m/s，流體出口邊界條件為壓力出口，出口壓力值為零，壁面采用無滑移的靜止壁面邊界條件。

2 結果分析

2.1 正常管道計算結果分析

通過研究以下兩種不同荷載組對正常管道的影響：工況1僅考慮流體；工況2考慮交通荷載、土壓力和流體的共同作用，比較分析不同負荷下的管道力學響應。利用ANSYS Workbench軟件進行模擬，其管道中湍流的發展持續時間為5 s,而交通荷載持續時間為10 s，模型計算時間為10 s，即交通荷載循環1次。

研究表明由于管道承口和插口部位等效應力較大，管道兩端增大的幅度更大，中間位置變化相對平緩；此外由于埋深產生的土壓力和流體產生的自重,管道底部的等效應力大于頂部的等效應力。工況2作用下管道的等效應力較工況1增加了約2.5倍，且工況1管頂和管頂等效應力隨縱向路徑變化比工況1更平緩，表明流體對管道的作用是有限的，但在多場耦合條件下卻不能忽略。

圖3為正常混凝土管道在工況1作用下承插口最大主應力云圖。從圖3中可以看出，插口在頂部表現為拉應力，在底部外表面表現為壓應力，與圖4工況2作用下的管道相比，正常混凝土管道在工況1下插口的最大主應力明顯低于在工況2下插口的最大主應力，且工況1下插口拉應力最大值點出現在管頂外表面附近，而工況2下插口拉應最大值點在在管頂外表面和兩側壁附近；工況1和工況2下承口的拉應力主要分布在內表面，壓應力分布在承口頂部外表面和底部內表面，且工況1承口拉應力較大的點在管頂附近，而工況2拉應力較大的點主要在兩側壁附近。

圖3 工況1下管道最大主應力

圖4 工況2下管道最大主應力

2.2 腐蝕管道計算結果分析

交通荷載、土壓力和流體對正常管道的力學響應有重大影響，而對腐蝕管道的影響缺乏了解，因此，以下分析兩種不同負荷組對腐蝕管道的影響：工況1僅考慮流體；工況2考慮交通荷載、土壓力和流體，比較分析不同負荷下的管道力學響應。管道中湍流的發展持續時間為5 s,而交通荷載持續時間為10 s，模型計算時間為10 s，即交通荷載循環1次。

圖5和圖6為管道位移歷時曲線。從圖5和圖6可以看出工況2作用下管道的位移變化量明顯大于工況1， 且工況2作用下管道的位移增長速率較快， 而該工況1作用下管道的位移增長速度較慢， 這說明流體對管道的作用是有限的， 但管道在多場耦合作用下流體的力學效應卻不能忽略； 腐蝕管道位移變化量在兩種工況下均大于正常管道的位移變化量。

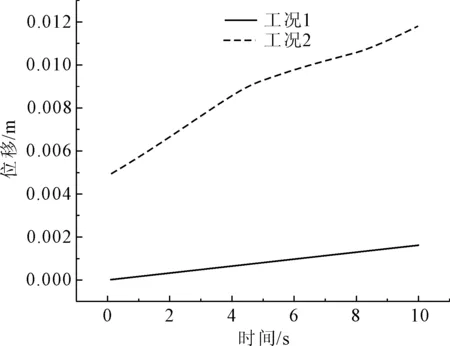
圖5 正常管道位移歷時曲線

圖6 腐蝕管道位移歷時曲線

圖7和圖8為管道橫截面環向等效應力曲線，可以看出，工況1作用下管道橫截面環向等效應力在環向角度為75°～125°和245°～295°之間管道會產生突變，最大應力發生在此兩處，而在其余各處等效應力曲線都較平緩；而工況2作用下的管道，整個等效應力曲線變化較快，起伏較大，但最大應力出現的位置與工況1相同。由圖7和圖8對比分析可得，工況1和工況2作用下腐蝕管道的等效應力大于正常管道等效應力，且正常管道和腐蝕管道最大應力在75°～125°和245°～295°之間都出現了應力集中現象，腐蝕管道等效應力變化趨勢比正常管道更快，而在環向角度為0°～25°、150°～200°和335°～360°之間，腐蝕管道等效應力小于正常管道等效應力，主要原因是交通荷載使腐蝕管道在管頂和管底出現了應力集中現象，相應的在環向其他部位應力會小于正常管道環向其他部位。

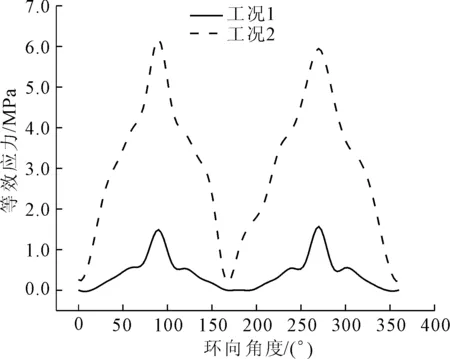
圖7 正常管道橫截面環向等效應力曲線

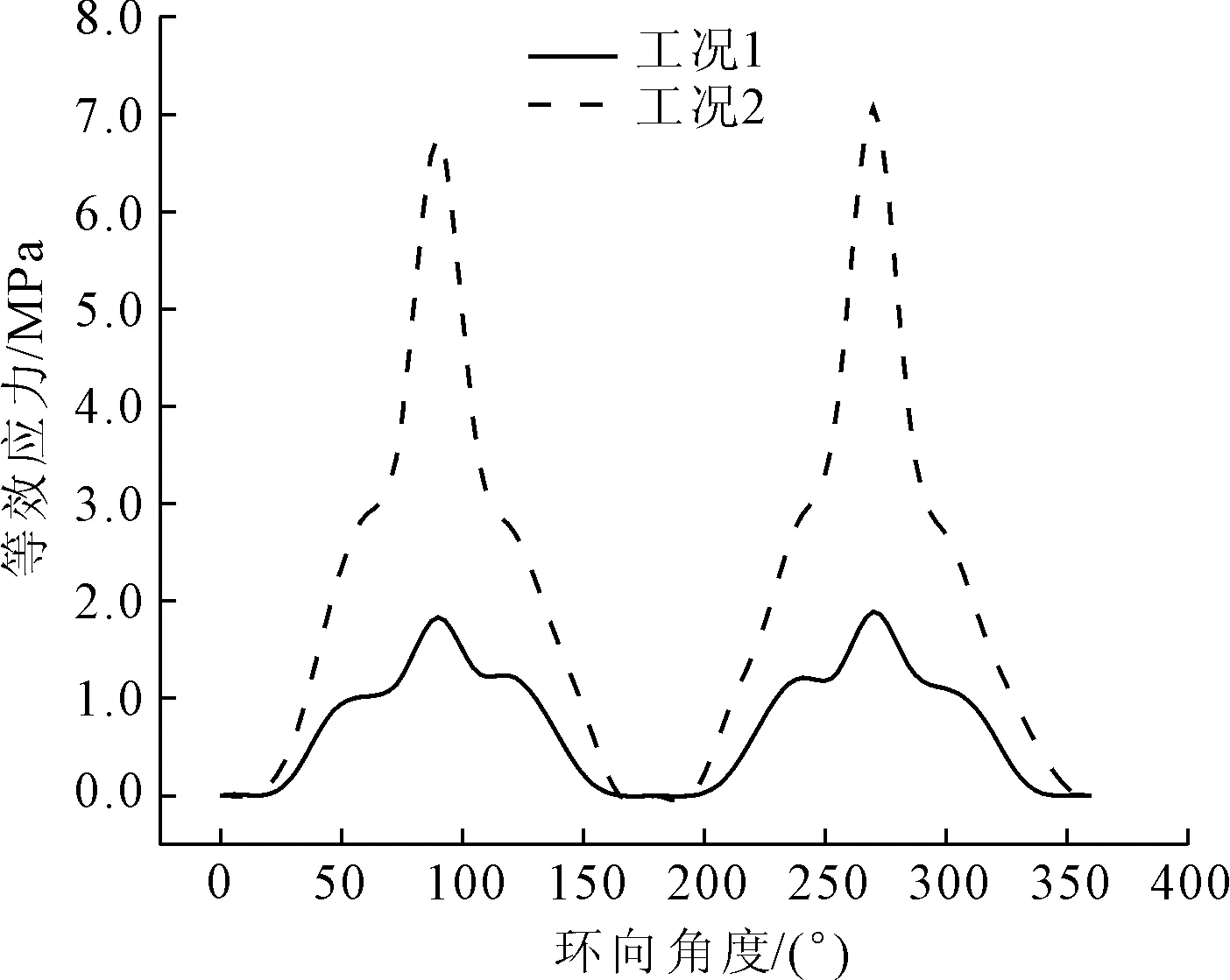
圖8 腐蝕管道橫截面環向等效應力曲線

3 結 論

基于混凝土排水管道，對氣液兩相流正常管道和腐蝕管道在不同的耦合作用下，以工況1僅考慮流體；工況2考慮交通荷載、土壓力和流體的共同作用進行了有限元分析，結論如下：

(1) 由于管道承插口的存在，等效應力在接頭會有所增大，且在管道兩端處增大的幅度更大。

(2) 管道插口在頂部表現為拉應力，在底部外表面表現為壓應力，工況1作用下插口的最大主應力明顯低于工況2作用下插口的最大主應力，工況2多場耦合的作用使拉應力的分布范圍更廣，在管頂外表面和兩側壁均存在。

(3) 管道承口的拉應力主要分布在內表面，壓應力分布在承口頂部外表面和底部內表面，且工況1作用下拉應力較大的點在管頂附近，工況2作用下拉應力較大的點主要在兩側壁附近。

(4) 流體對管道的作用是有限的，但在多場耦合作用下的流體的力學效應卻不能忽略；腐蝕管道位移變化量在兩種工況下都大于正常管道。

(5) 工況2下管道在管頂和管底出現了應力集中的現象，且使腐蝕管道橫截面環向的等效應力比工況1變化更快，因此，考慮工況2多場耦合作用對腐蝕管道的影響更大，使其更易產生破壞，應該高度重視。