基于MIKE11(HD)的農用灌排水非恒定流算例分析

牛瑤瑤

(盤錦市水利勘測設計有限公司，遼寧 盤錦 124010)

隨著計算機信息技術的迅猛發展，以及人們對農用灌排水系網模擬分析要求的不斷提高，可視化理論及相關算法應運而生，而各式各樣的流水模擬軟件系統更是為環境模擬及河流水動力方案制定等提供了高可靠、高精準的技術支持。

各國學者在很早就對非恒定流理論展開了廣泛且深入地探索與研究，并針對恒定流狀態的適用性問題進行了全面分析。通過以下2種計算方法的優缺點直觀對比后發現，如果采用恒定流方程式計算水面線，步長選擇會對成果精準性產生很大影響，而且在現實操作中很難掌控。如果采用非恒定流方程組推導水面線，可對恒定流狀態的整個演進過程進行完整描述。盡管第二種算法的運算量很大，但能為計算成果提供更多有效信息，最關鍵的是能從根本上保持可靠的穩定狀態。因為斗溝末端、研究區支溝的水流全部匯入干溝，所以斗溝、支溝的水位會直接受匯流區影響，而且流水運動情況較為復雜，在此情況下，如果采用恒定流理論進行求值計算，一般很難獲取精準、可靠的成果。但非恒定流模型卻能憑借獨有的概化流水優勢妥善解決該問題。因此，在本研究中，為進一步驗證非恒定流理論在小型農田排水工程應用中的可靠性，筆者采用了當前備受業界人士推崇的MIKE11水動力學模型(HD)作為計算平臺。

1 計算平臺MIKE11水動力(HD)模型

水動力學模型(HD)是MIKE11最重要的一個組成部分，它依托非恒定流理論設計而成。在對HD模型的運行機制進行深入分析后發現，它引入了專業的追趕解析法和6點Abbott-lonescu格式離散圣維南方程組，其計算格式具體如圖1所示。整體來看，該方法先對水系網進行離散處理，使其成為更容易計算的交替網絡，之后再按照既定順序對各節點的過流量(Q點)及水位(h點)進行交替計算，其計算過程具體如圖2所示。

圖1 基于Abbott-lonescu格式的6點計算

圖2 Abbott格式過流量點與水位點交替布設

對每一h點解析連續性方程，解析格式如圖3所示。

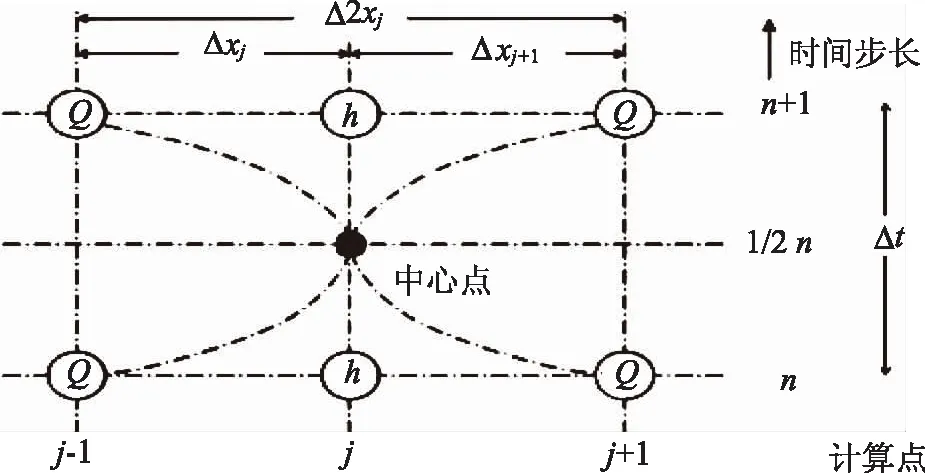
圖3 Abbott格式6點連續性解析方程

2 構建研究區MIKE11水動力學模型

案例MIKE11水動力學模型構建是一個復雜的過程，不僅要建立6個文件，還要將各文件涉及的相關數據進行有效匯總。模型的構建過程為：①建立水系網文件；②選取截面數據；③確定邊界條件，建立相匹配文件；④參考計算成果，建立時間序列文件；⑤明確起始條件，建立參數文件；⑥確定計算時間步長，建立模擬文件。其構建流程具體如圖4所示。

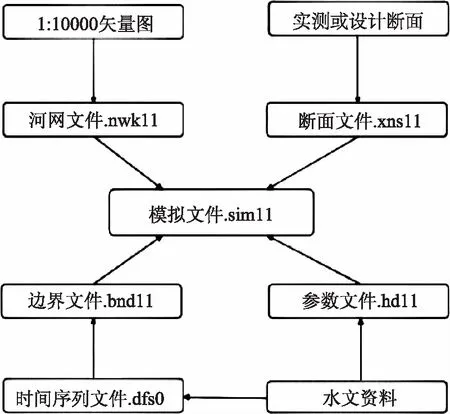
圖4 基于MIKE11的一維水系建模流程

利用建好的6個文件對水系網進行一維概化，由此便可對河道洪水情況進行全程模擬，從而為計算成果提供可靠且有效的數據支持。

2.1 數字水系網

將已掃描完成的水系網底圖導入MIKE11水系網編輯頁面中，各河段則選用水系網文件編輯器進行定義，再將河段信息(包括長度、河道部位等)完整地導入模型中，以生成所需的數字水系網，具體如圖5所示。其中R1用來描述干溝，F1～F12分別用來描述12條支溝，Z1～Z4用來描述4條斗溝。

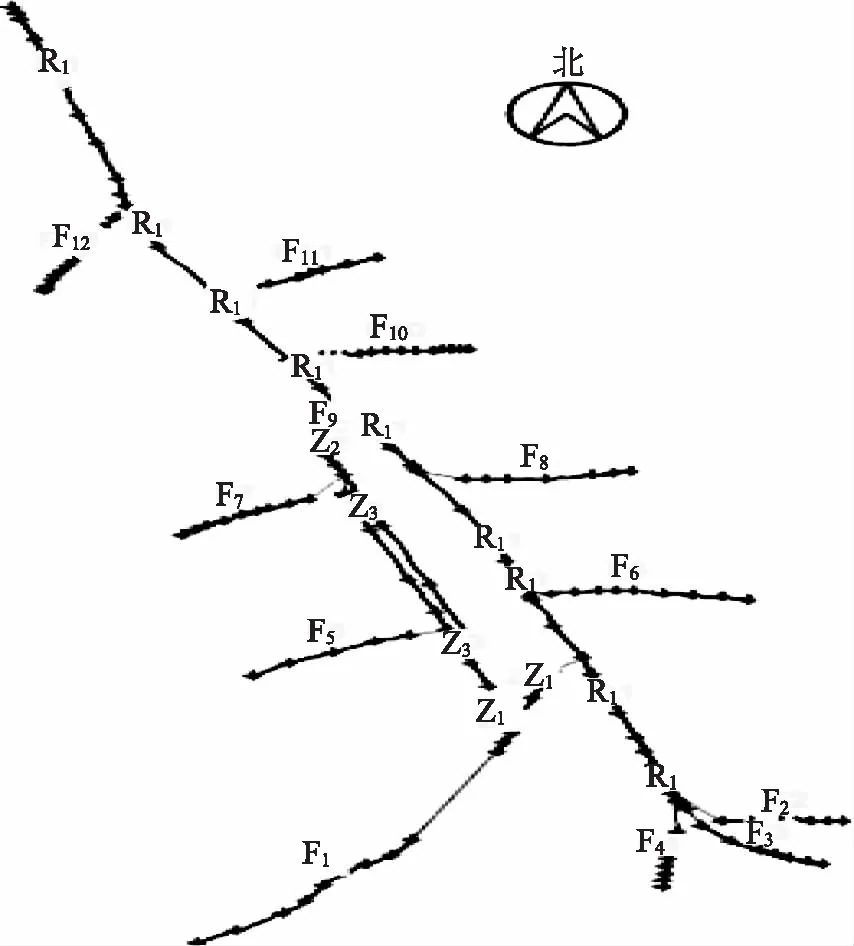
圖5 數字水系網

2.2 河道截面

把截面計算成果精準無誤地導入截面文件編輯器中，參考地形高度，再將河道的截面x、z數據導入其中，由此完成截面文件構建操作。需依據現場地形及河道長度確定各河道的截面間距。生成的截面文件如圖6所示。研究區干溝總共細分為35個截面，支溝、斗溝截面數量及間距均需要按照現場地形特點來確定。

2.3 時程序列

在本研究中，將案例雨量站搜集數據作為參考資料，同樣按照傳統方法確定河道底坡和邊坡常數、規范排澇設計標準。因為研究區暴雨覆蓋面積高達4.02km2，根據現行規范需參考案例區域洪峰過流量經驗公式計算出洪水過程線(案例區域水文總站，1977年)，關于案例區域概化洪長過程比值更多詳情可見表1，Qi/Qp為洪峰過流量比率，Ti/τ為匯流時長比率。

表1 案例區域綜合概化洪長過程比值

根據規范要求，直接推導出河道洪峰過流量：

(1)

式中，C1—與P相關的參數，翻閱規范后得知，C1在P=20%時取值0.056；Qp—P設計頻率所形成的洪峰過流量，m3/s；H24p—24h設計暴雨量，本文取值153.05mm；F—匯水面積，km2；θ—地理要素。

圖6 截面文件

(2)

式中，J—河道坡降；L—河道長度。

可直接推導出河道流水的匯流時間：

(3)

式中，K—匯流常數，翻閱規范后得知，它與θ相關；Qp—設計頻率為P時形成的洪峰過流量，m3/s；其他變量含義同前。

根據表1計算出研究區各河道的洪峰過流量過程線，由此生成的成果具體可見表2—4，q基指的是7d以內洪水基流模數，取值0.07(s·m3)/km2，所以Q基=q基×F。

表2 干溝洪峰狀態過流量

表3 支溝8洪峰狀態過流量

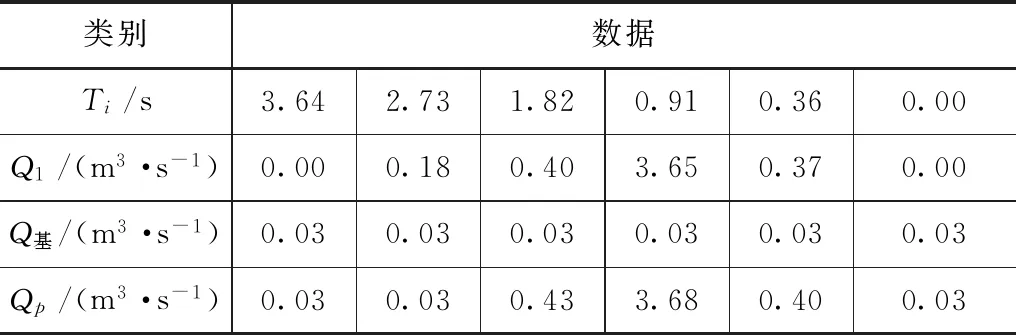
表4 斗溝3洪峰狀態過流量

寫入起始時間，然后分別確定干溝、支溝和斗溝的模擬類型，其中前者選用水位和過流量模型，而后二者選用過流量模型。將通過計算獲得的河道洪峰過流量過程線有序輸入以構建時間序列文件。干溝時間序列文件具體如圖7所示，同理，利用此方法可生成其他河道的文件。

2.4 邊界參數

(1)內、外邊界條件。支溝、干溝、斗溝均通過Open狀態進行邊界表達，并設定為inflow邊界類型。

(2)河床糙率及起始水位。將起始過流量設置為0，可達到理想收斂效果；為保證模型順利完成計算，需根據河床高度設定起始水位。在本研究中，起始水位為起算部位河床高度0.51m；由于糙率取值是關乎計算成果是否精準的一個重要環節，因此，在本研究中要充分考慮河道實際情況，以確定出最理想的糙率值，最終取值0.03。

3 基于MIKE11水動力(HD)模型的算例成果

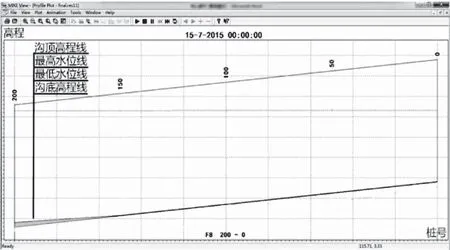
將上文構建的各類文件進行有效匯總，以10s為時間步長進行計算。按照傳統算法逐一計算出起始水位、糙率常數和邊坡值，并根據現場實際及非因為少數溝段存在很大坡降，在工程量限定的條件下，就難以防止沖刷現象的發生。所以土質河道的流動速率只有控制在0.4m/s

圖7 干溝時程序列顯示文件

表5 河道截面規格非恒定流計算

各溝段水位模擬情況如圖8—10所示。其中，樁號用橫坐標表示，高度用縱坐標表示，實線為最高水位線，虛線為最低水位線，單位均為m。

通過上述分析進一步了解到，經過起始試算溝深的多次優化，本工程的最高水位線均位于溝頂高度線以下，也就說明不存在漫頂危險，而且截面設計規格也達到了排洪要求。由于該地區對地下水位無特殊要求，因此河道無需排漬設計。通過非恒定流理論方法得知，河道水位較大，為便于后續施工，選取了比傳統算法高的底寬值，經多次優化后確定了截面規格。

圖9 支溝8截面設計(單位：m)

圖10 斗溝3截面設計(單位：m)

4 結語

本研究對非恒定流理論的運行機制進行了深入探討，并對它在小型農田排水工程應用中的可靠性進行了驗證。經過模擬計算得知，通過起始試算溝深的的多次優化，本工程的最高水位線均位處溝頂高度線以下，也就說明不存在漫頂危險，而且截面設計規格也達到了排洪要求。流動速率核校成果表明，一些坡降較大的溝段存在著沖刷現象，河道匯流處流速相對緩慢，容易形成淤積，但其他河道流速均達到了不沖不淤的要求，進而證實了非恒定流理論截面設計的可靠性與有效性。