基于小波理論的艦船IMU加速度計信號處理算法

徐博，劉斌*，劉德政，崔耀虎，鄧偉

1 哈爾濱工程大學 自動化學院，黑龍江 哈爾濱 150001

2 天津津航技術物理研究所，天津 300192

0 引 言

由于慣導系統工作環境的復雜性，加速度計信號在采集和傳輸過程中不可避免地存在噪聲，而如何去除加速度計數據中的噪聲分量，成為捷聯慣性導航系統（以下簡稱“捷聯慣導系統”）中數據處理的一項關鍵技術。本文將從艦船捷聯慣導系統對加速度參數高分辨率、寬動態范圍的設計要求入手，研究并完成艦船慣導加速度計輸出信號的高精度采集與處理工作。對慣導系統而言，慣性器件的測量精度不僅包括相關慣性元件本身的精度，還包括其數據采集系統的精度，如何利用小波分析在信號處理中的優越性來實現慣導信號的高精度采集與處理，已成為慣性技術領域的一個研究熱點和方向。

在捷聯慣導系統中，機械結構諧振、傳感器噪聲和溫度漂移等都是影響導航精度的主要原因，如何消除慣導系統在信號采集過程中產生的噪聲影響成為實現高精度導航的關鍵[1]。目前，在此系統中通常采用FIR濾波[2]、最小均方（LMS）[3]、維納（Wiener）濾波[4]、卡爾曼濾波（Kalman filter）[5]、粒子濾波（particle filter）[6]等方法對慣導加速度計信號進行降噪處理。其中，FIR濾波可以對信號進行線性相位濾波，可通過設計數字濾波器的方式將信號與噪聲分離，然后保留某一頻段內的信號作為輸出。但這種方法只適用于有用信號和噪聲的頻譜沒有重疊的情況，而且所需要的濾波器階數較高，這會使得整個處理過程計算量較大，很難滿足系統實時性的要求[7]。

小波降噪理論在近幾年得到了迅猛發展。1994年，Donoho正式解釋了“小波降噪”的含義，即通過對小波系數進行閾值量化處理來實現分層濾波的效果[8]。Mallat是最早將計算機理論中的多尺度分析思想引入小波分解過程中的人，并于1994年提出了小波分解與小波重構的快速算法，也即Mallat算法[9]。隨后，斯坦福大學以Donoho為首的學術團體又提出了小波閾值濾波算法，并取得了大量的理論及實際應用成果[9]。

基于上述研究，本文擬提出一種新型的小波閾值降噪算法，該算法能對信號中的高斯白噪聲等噪聲進行有效濾除，并能在一定程度上避免經典去噪方法造成的信號高頻部分信息丟失，可滿足信號處理的實時性要求。

1 小波去噪理論

1.1 小波閾值去噪方法

小波閾值濾波的原理是：通過小波分解，在小波域內把有用信號的能量集中在一些幅值較大的小波系數上，而白噪聲的能量卻分布在整個小波域內，且分解后有用信號的小波系數幅值要大于噪聲信號的系數幅值。因此，應通過在不同尺度上選取合適的閾值來對小波系數進行處理，若小波系數小于該閾值，則判斷為噪聲分量，將其置零，保留大于該閾值的小波系數，從而實現對噪聲的抑制。最后，進行小波逆變換，完成信號的小波重構過程。

含噪的一維信號模型可表示為如下形式：

由圖1可知，小波閾值去噪過程的一般步驟如下[10]：首先，對原始含噪信號進行多尺度的小波分解；然后，根據信號特征計算得到各尺度下的小波閾值估計值，并對各分解尺度下的小波系數進行閾值量化處理；最后，將完成閾值處理后的各層小波系數進行重構運算，得到去噪后的輸出信號。在這3個步驟中，最關鍵的步驟是閾值估計以及如何對小波系數進行閾值處理，在某種程度上，它關系到信號降噪的質量。

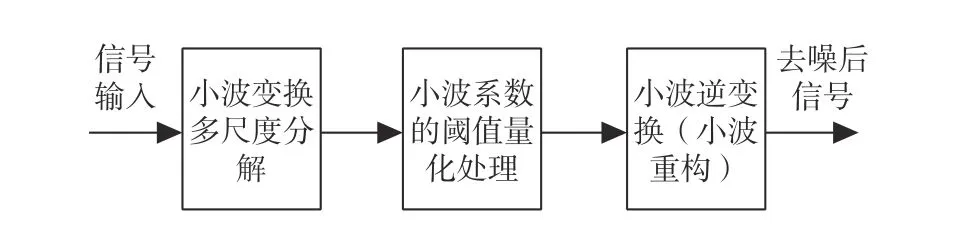
圖 1 小波去噪流程圖Fig. 1 Flow chart of wavelet denoising

1.2 改進型小波閾值濾波

小波閾值濾波的關鍵在于閾值估計以及閾值函數的選取。目前，常用的閾值處理方法有2種：硬閾值函數和軟閾值函數。

硬閾值函數[11]：

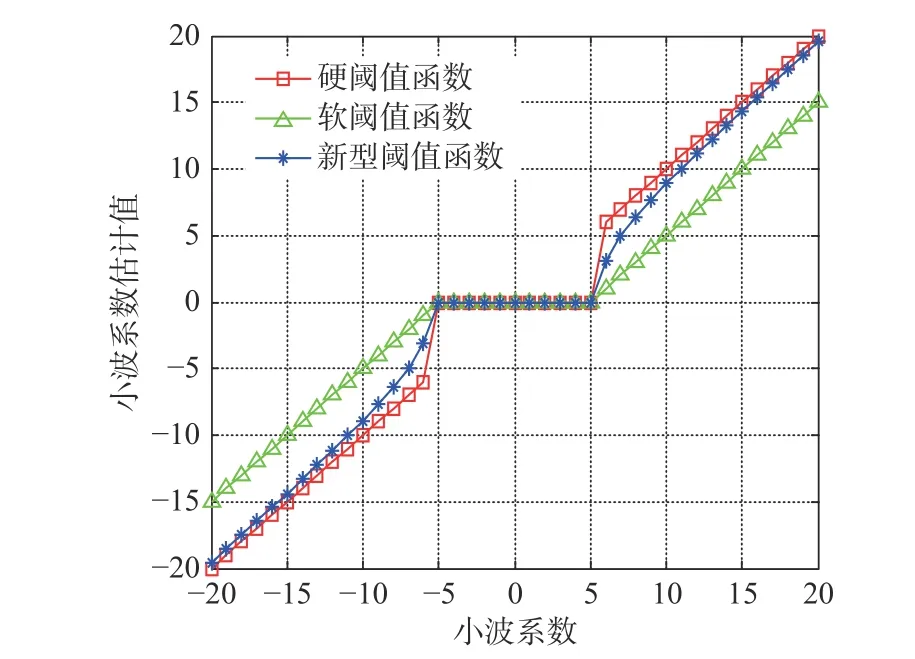
圖 2 3種閾值函數對比Fig. 2 Comparison of three threshold functions

利用不同閾值函數對同一噪聲信號進行處理，處理結果如圖3所示，并將不同閾值函數處理所得誤差進行對比，如圖4所示。

利用各種閾值函數對Heavisine信號去噪后的信噪比（signal to noise ratio，SNR）和均方根誤差（root mean squared error，RMSE）如表1所示。

從圖3、圖4和表1中可以看出：硬閾值函數去噪后的波形中存在較多毛刺，信號平滑性較差；通過軟閾值函數處理得到的信號波形雖然光滑，但信號重構精度較差，信噪比較低；利用新型閾值函數處理得到的信號較為光滑，SNR和RMSE均優于其他閾值函數，并且計算相對簡便，具有更高的實用價值。

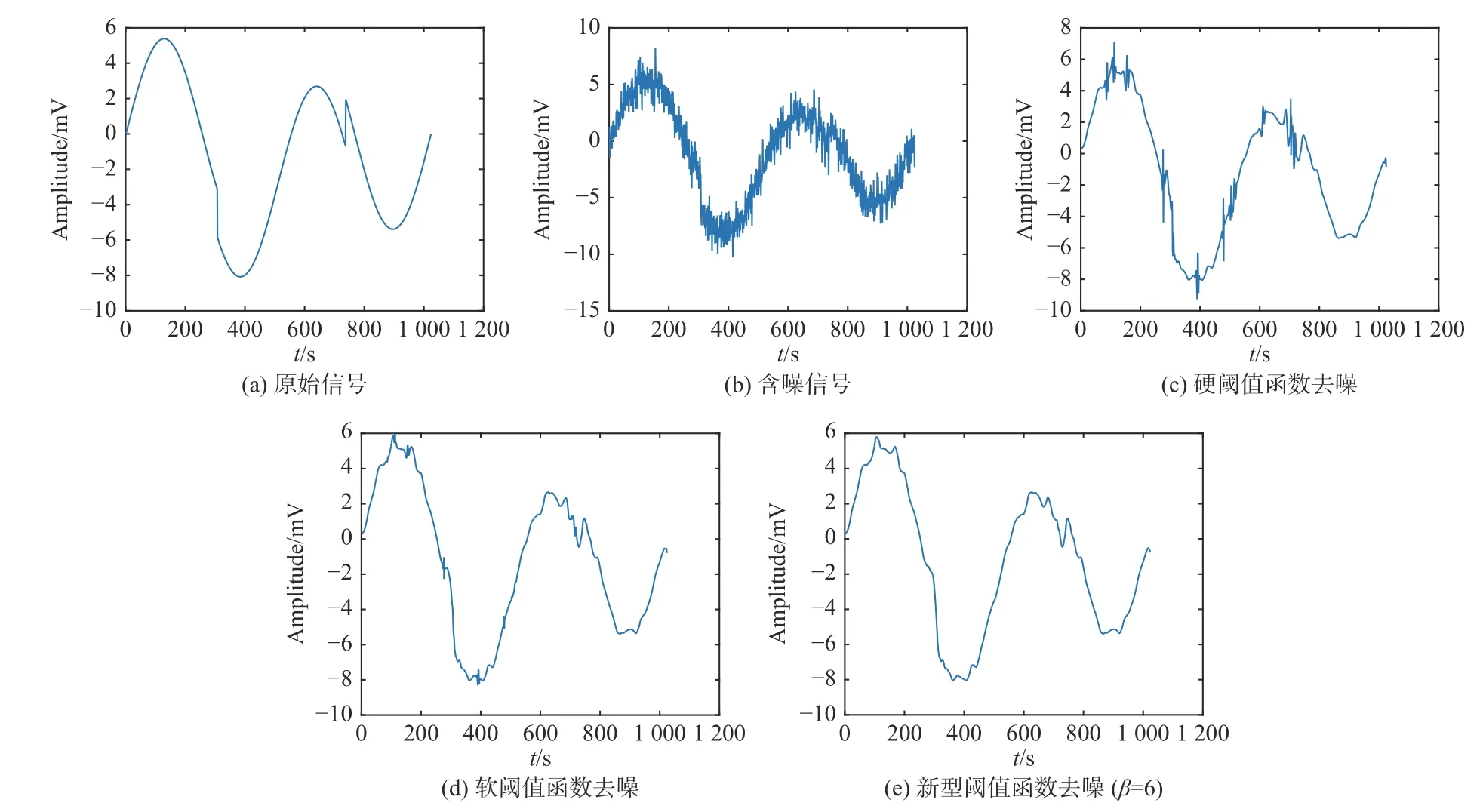
圖 3 不同閾值處理函數的去噪效果比較Fig. 3 Comparison of denoising effects of different threshold processing functions

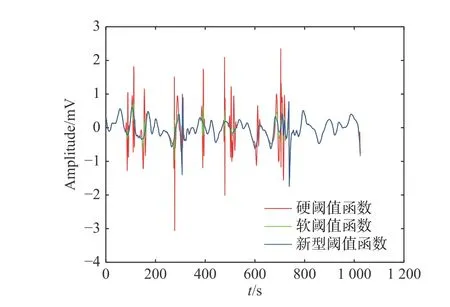
圖 4 不同閾值處理函數誤差對比圖Fig. 4 Error comparison of different threshold processing functions

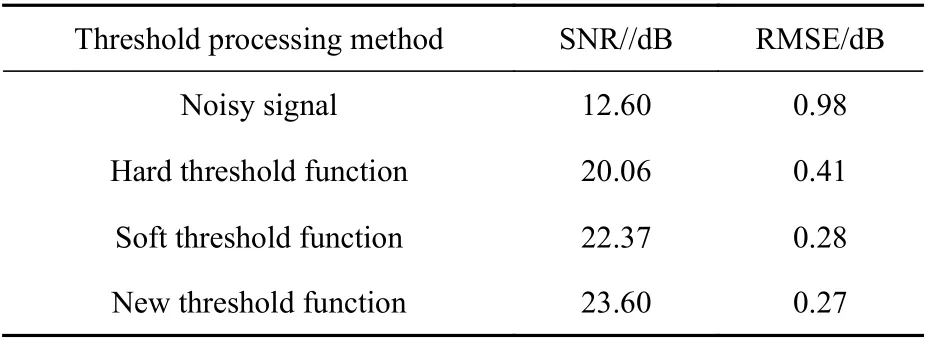
表 1 不同閾值函數去噪后信噪比和均方根誤差比較Table 1 Comparison of SNR and RMSE after denoising by different threshold functions

2 基于Mallat算法的小波降噪FPGA實現

2.1 Mallat算法

為實現信號的快速分解與重構，Mallat將多尺度分析的思想引入到了小波分析中并提出了Mallat算法[13]。根據Mallat算法，小波分解的數學表達式為

由于濾波器長度有限，為便于計算，分別將小波分解和重構表達式轉換成了易于實現的形式，即

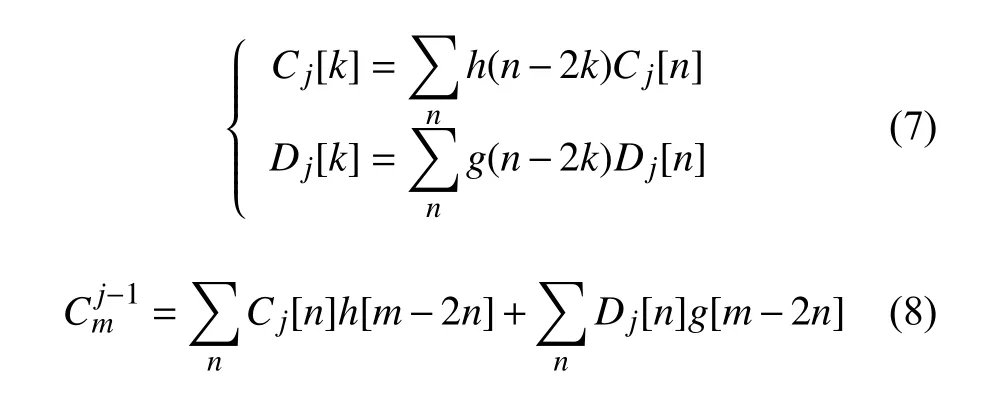
根據Mallat算法理論，本文選用DB3小波基對經過A/D轉換后的加速度計信號進行三階的小波分解與重構。

2.2 延拓模塊

在Mallat算法的推導中，是假定輸入序列為無限長，而在實際應用中，輸入序列為有限長，此時，濾波器系數與輸入序列進行卷積就會出現“輪空”現象。因此，可在設計中采用對稱延拓的方法來減少在邊界處的卷積誤差，從而有效避免輸入序列邊緣不連續的問題。

由于設計中采用的是DB3小波基，其對應的濾波器長度為7，因此原始信號兩端需要延拓的數據長度為5（filterLen-1）。ModelSim仿真結果如圖5所示。

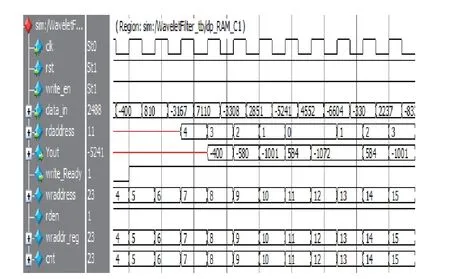
圖 5 延拓仿真圖Fig. 5 Extension simulation diagram

2.3 濾波器模塊

無論是小波分解還是重構，都是通過數字濾波器來實現的，濾波器模塊是整個運算的核心部分。由式（7）和式（8）可知小波分解和重構的實質都是卷積運算，由于小波基選擇的是DB3，為優化結構設計，需要設計5級流水的濾波器，主要由乘法器和加法器組成。

在濾波器設計過程中，涉及到浮點數的運算，通過研究對比現有的基于FPGA的浮點運算方法[14]，在本設計中，首先將濾波器系數量化成16位精度模式，然后在濾波器中對卷積運算的輸出數據作截取處理，即右移16位作為濾波結果。其中，小波重構低通濾波器ModelSim仿真結果如圖6所示。

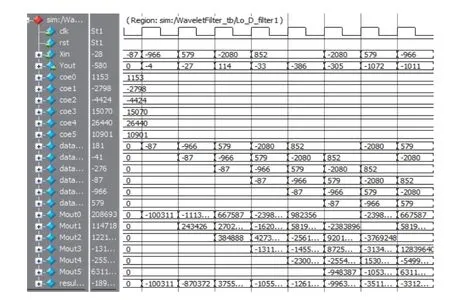
圖 6 低通濾波器ModelSim仿真Fig. 6 Low-pass filter ModelSim simulation

2.4 閾值處理模塊

小波去噪的關鍵在于閾值的確定以及閾值函數的選取。為保證各尺度下小波閾值的準確性，本文采用分層閾值估計方法，其函數表達式為

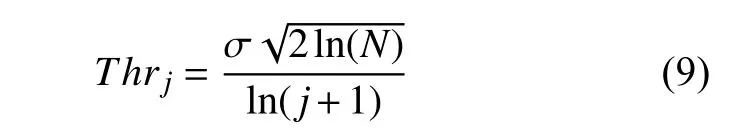
式中：N為采樣點數；σ為信號噪聲標準差。但在實際工程中，噪聲標準差是不知道的。如果采用硬件計算方法求解閾值，不僅需要對噪聲進行估計，還需要進行開根號等運算，硬件實現相對復雜[15]。利用Matlab軟件對加速度計數據進行分析，計算出不同尺度下每一分解層不同的閾值，然后再將計算得到的閾值存入FPGA的參數RAM中，在進行小波閾值處理的過程中，直接從RAM中完成讀取。

圖7所示為新型小波閾值去噪FPGA實現流程圖。該模塊的具體設計辦法為：首先，將各層小波系數進行相應的移位和帶符號位擴展，實現對各層小波系數絕對值與已設定相應層閾值大小的判斷[16]；然后，利用新型小波閾值處理函數對小波系數進行處理，對算法中涉及到的乘法或者除法進行運算，在設計中主要是利用FPGA內置的IP核LPM_MULT和LPM_DIVIDE實現；最后，進行位數截取以得到新的小波系數結果。

3 實驗結果分析

3.1 仿真實驗分析

設計中，使用Altera公司的EP4CE22F17 FPGA作為系統核心控制處理單元，系統時鐘為64 MHz。在驗證過程中，首先通過ModelSim和Matlab等

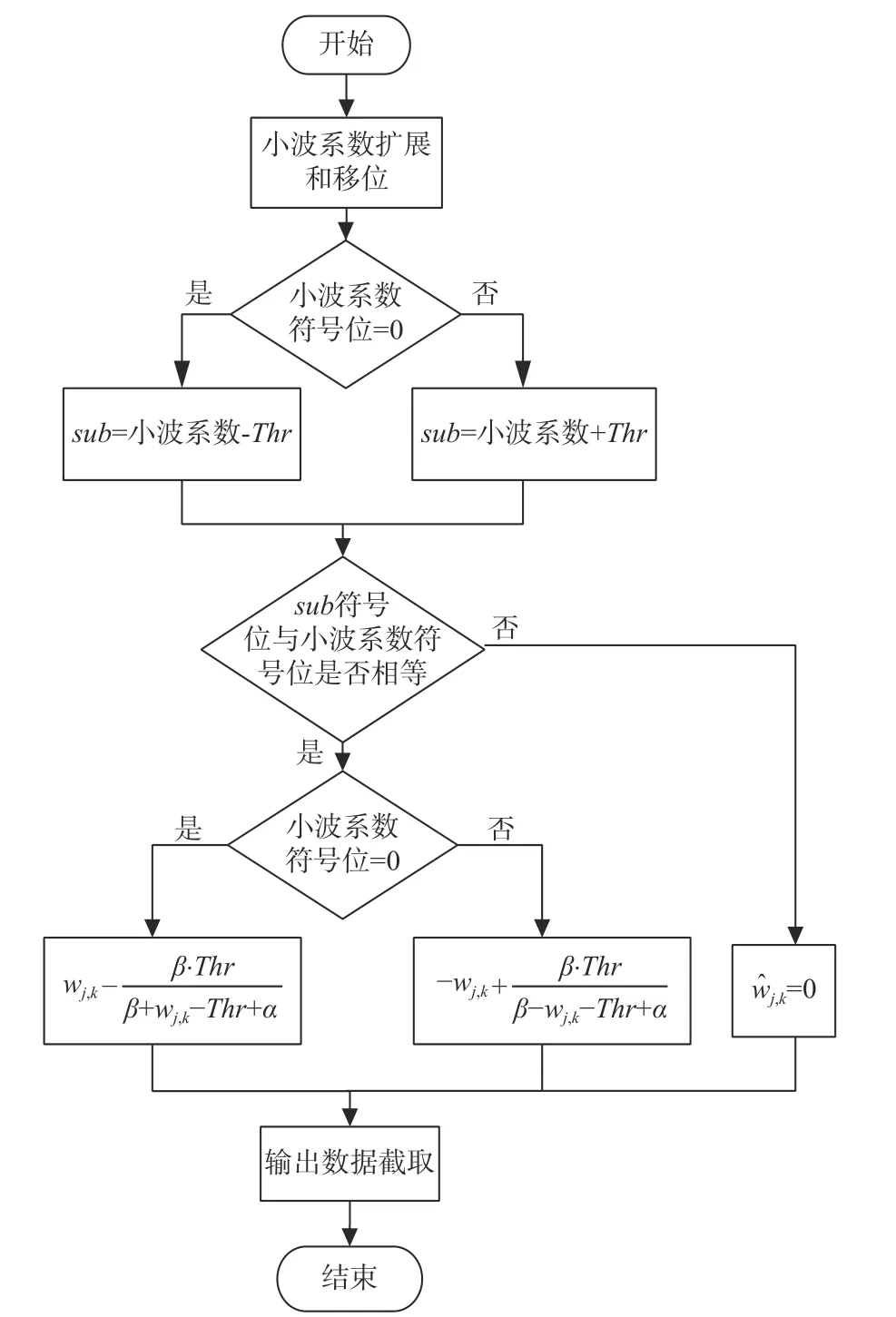
圖 7 新型小波閾值去噪FPGA實現流程圖Fig. 7 Flow chart of implementation of the new wavelet threshold de-noising in FPGA

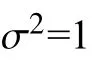
利用改進型閾值函數法進行信號去噪處理后的信號波形得到了明顯改善。為進一步反映基于FPGA實現的小波去噪算法的降噪效果，將FPGA的仿真結果以二進制文本形式保存并在Matlab中進行了分析處理，如圖8所示。利用信號處理前后的RMSE和SNR這2個客觀標準，進一步驗證了這種閾值去噪方法的良好去噪效果，如表2所示。

圖9（a）為原始帶噪信號。圖9（b）為經過小波降噪處理后的信號，圖中對Matlab與FPGA小波實現結果進行了對比，結果顯示其略有差異，這是由于在FPGA運算過程中位截斷和數據取整造成了數據丟失。圖9（c）為利用傅里葉分析進行濾波后的信號。從圖中可以發現，該濾波器無法準確還原信號，不能將有用信號的高頻突

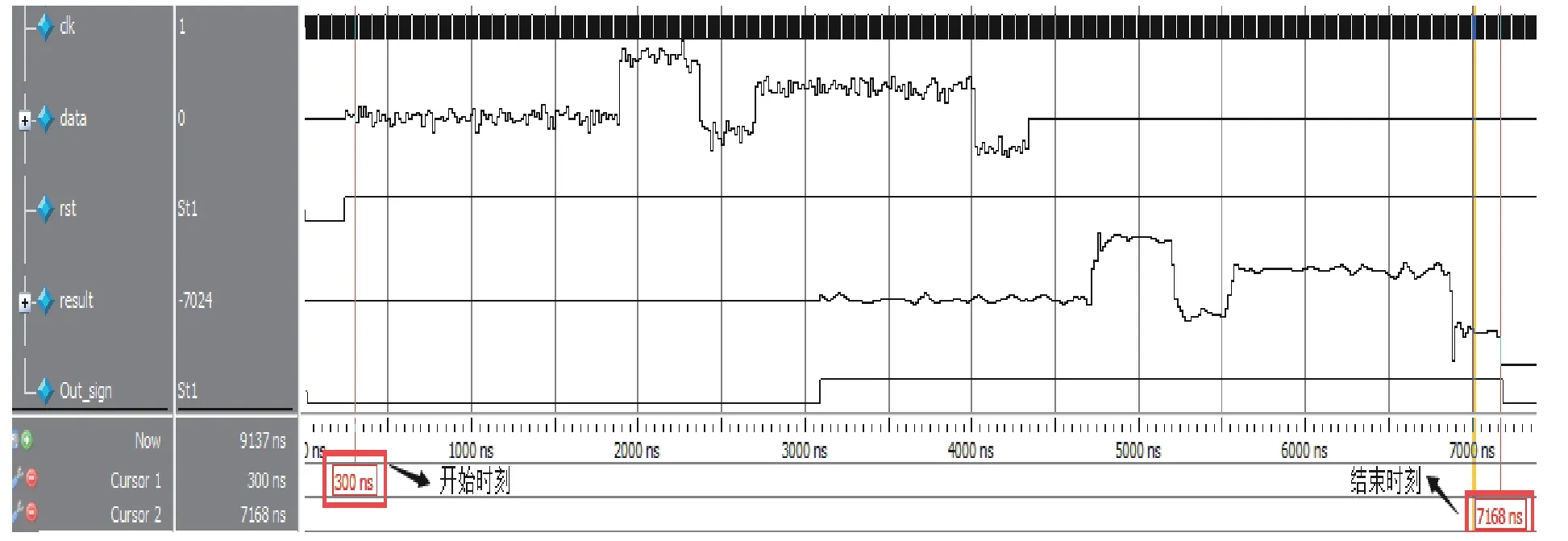
圖 8 ModelSim仿真結果Fig. 8 ModelSim simulation results

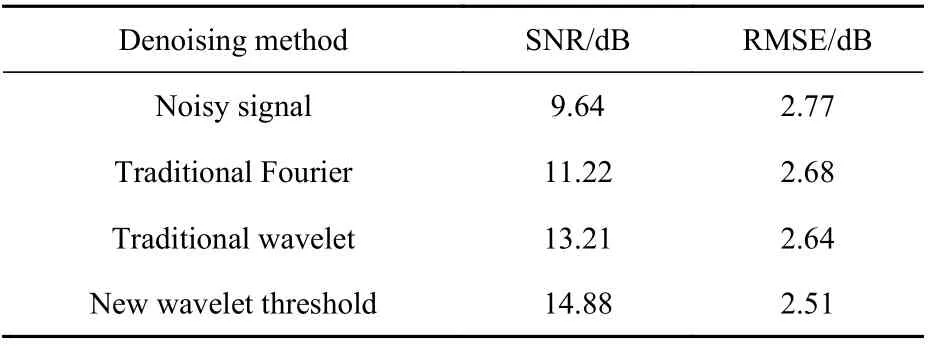
表 2 信號去噪效果比較Table 2 Comparison of signal denoising effects

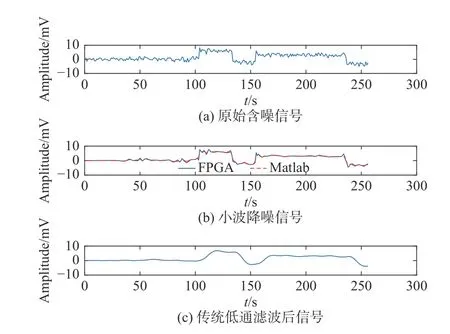
圖 9 小波去噪效果比較Fig. 9 Comparison of wavelet denoising effects

變部分與噪聲引起的高頻干擾加以區分。通過對比圖9（b）和圖9（c），驗證了小波降噪算法具有更高的信噪比，對信號的高頻突變處理效果更加顯著。

3.2 加速度計測試結果分析

為驗證本文所提方法在工程應用上的價值，對靜態條件下的加速度計輸出信號進行了采集測試，實驗測試結果如圖10所示。

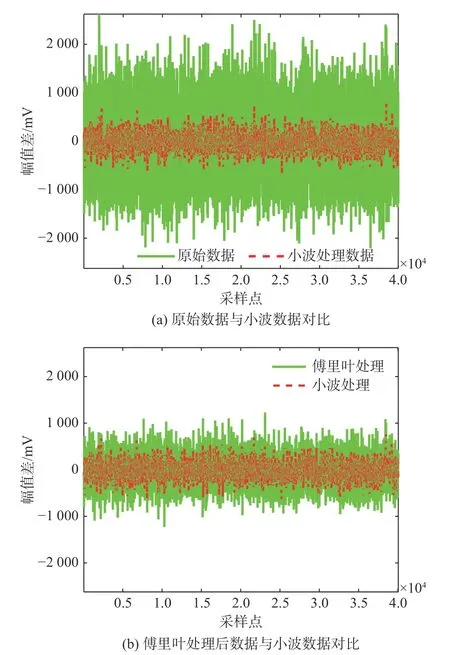
圖 10 數據對比Fig. 10 Data comparison

圖10（a）為測試原始數據與小波模塊處理后數據分別減掉均值后的數據分布圖。從圖中可以看出，未經處理的原始數據信號幅值變化較大，大部分數據在±2 000 mV范圍內跳動，而經過小波降噪模塊處理后的數據則相對穩定，主要在±500 mV內波動。圖10（b）為利用傅里葉濾波器處理后的數據與小波模塊處理后數據分別減掉其均值后的數據分布圖。從圖中不難看出，相比未經任何處理的原始數據，兩者的信號穩定性均得到了改善，但經過傅里葉處理后的信號變化幅值還是較大，主要變化范圍在±800 mV內。

現對動態條件下的加速度計輸出信號進行采集測試。動態試驗環境為：三軸轉臺模擬搖擺試驗數小時，搖擺周期8 s，搖擺角度0.6°。實驗測試結果如圖11所示。

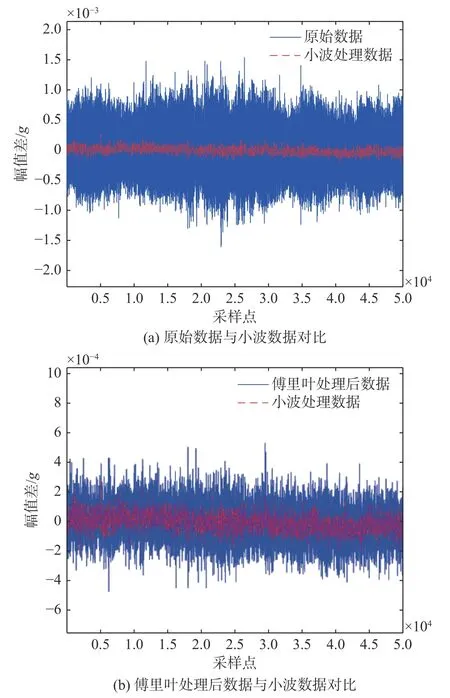
圖 11 動態數據對比Fig. 11 Dynamic data comparison

圖11（a）為測試動態情況下的加速度數據與小波模塊處理后加速度數據分別減掉轉臺真實值后的數據分布圖。從圖中可以看出，未經處理的原始數據信號幅值變化較大，大部分數據在±0.001g范圍內跳動，而經過小波降噪模塊處理后的數據則相對穩定，主要在±0.000 2g左右波動。圖11（b）為利用傅里葉濾波器處理后的數據與小波模塊處理后數據分別減掉轉臺真實值后的數據分布圖。從圖中不難看出，相比未經任何處理的原始數據，兩者的信號穩定性均得到了改善，但經過傅里葉處理后的信號變化幅值還是較大，主要變化范圍在±0.000 4g左右。

圖12所示為利用傅里葉和小波處理后的數據頻譜分布圖。經過上述2種濾波處理后的數據高頻噪聲均得到了很好的抑制，但仔細研究可以發現，傳統的傅里葉低通濾波器在對信號進行處理的過程中有“一刀切”的缺點，也即保留了所有的低頻信息，將通帶之外的頻譜不加區分地全部濾掉了，而相比傅里葉變換，小波降噪處理則顯得更加靈活。由圖12（b）可以看出，小波降噪處理是通過在不同尺度上選取合適的閾值來對小波系數進行處理，若小波系數小于該閾值，則判斷

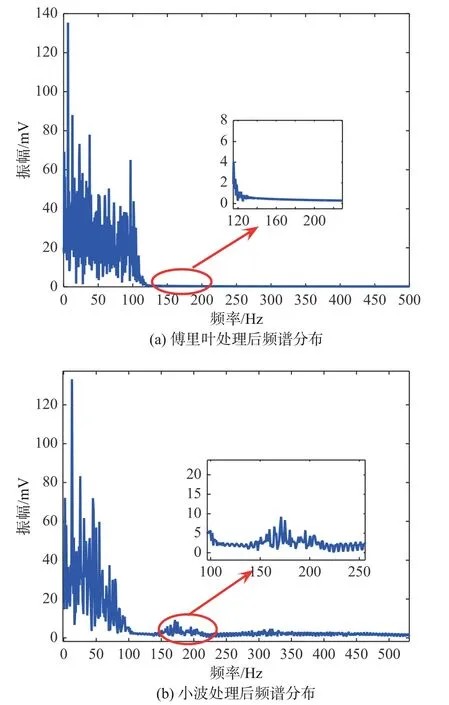
圖 12 頻譜分布Fig. 12 Spectrum distribution

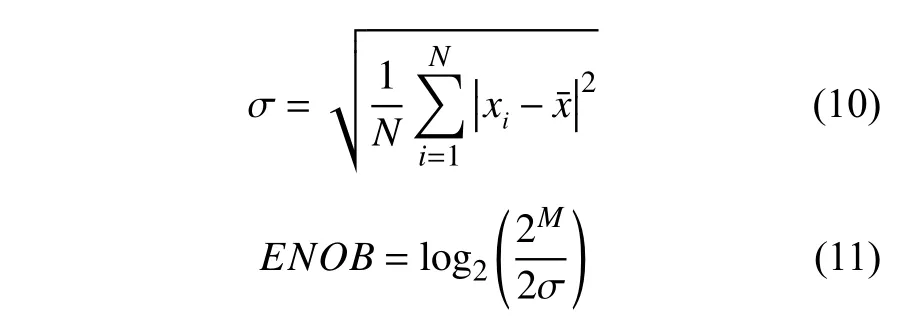
為了更加直觀、有效地分析小波算法的性能，分別對上述測試數據進行了計算統計，結果如表3所示。

由表3的計算結果可知，直接通過艦船IMU加速度計采集電路得到的原始數據ENOB可以達到20.8位以上；利用傳統傅里葉低通濾波器和小波降噪模塊均能改善信號質量，有效分辨率分別可以達到21.7位和22.4位以上，但是在計算濾波器參數時發現，因傳統傅里葉濾波器的階數較高，使得整個處理過程的計算量較大，而小波降噪模塊只需要完成3層變換就可滿足上述指標。因此由以上分析可以看出，小波降噪模塊在信號降噪方面具有較為明顯的優越性。

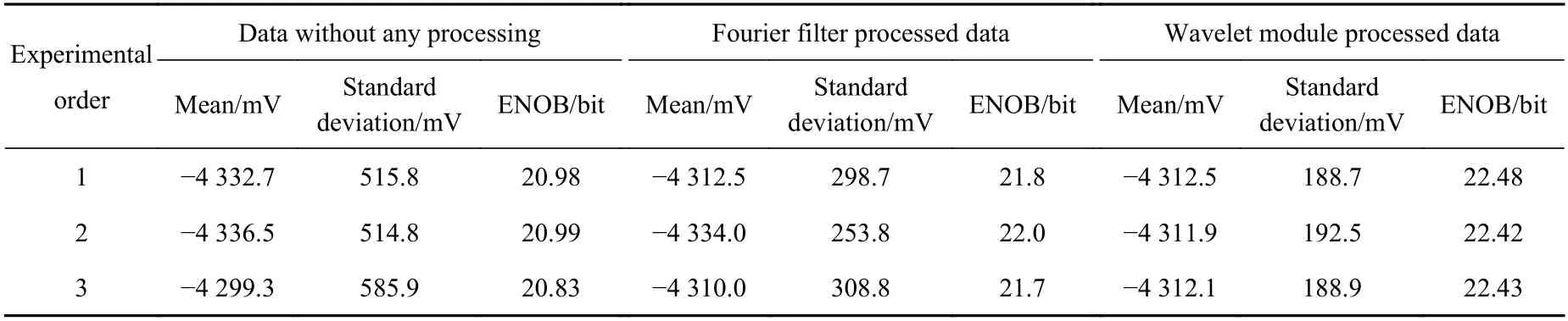
表 3 小波算法性能分析Table 3 Performance analysis of wavelet algorithm

4 結 語

本文在介紹小波去噪基本原理的基礎上，提出了一種改進型小波閾值濾波算法，通過與傳統的頻域去噪方法進行對比驗證，得出小波去噪可以很好地對高斯白噪聲進行降噪處理，有效解決了傳統頻域濾波方法的局限性。最后，利用FPGA對小波閾值算法進行了硬件實現。實驗結果表明，利用新型小波算法處理后的加速度計采集電路有效分辨位數能夠達到22.4位以上，相比原始信號，其有效分辨率提高了1.6位，證明小波算法具有較好的工程應用價值。但該降噪算法的閾值估計采用的是固定閾值，在下一步的工作中，還需要對自適應閾值進行研究以滿足系統動態性能要求。