間歇通信環境下的船舶編隊控制

劉睿，于雙和，尹廣帥

大連海事大學 船舶電氣工程學院，遼寧 大連 116026

0 引 言

隨著航海技術的發展，國內外許多學者非常關注多艘船舶編隊作業的控制研究[1-2]。為實現編隊控制，船舶之間需要彼此通信來獲得所需的信息。在不同環境下，由于船舶通信會受到不同因素的干擾，所以需要尋找不同通信問題的解決方法[3-4]。

船舶編隊控制通常包括 3種方法：領導—跟隨法、虛擬結構法和基于行為的控制方法。其中，領導—跟隨法[5]的應用范圍最廣,但是如果領導者失控，整個系統就會崩潰。而采用虛擬領航者[6]能很好地解決此問題。Fu等[7]考慮了外部干擾下船舶的編隊問題，并利用神經網絡估計了環境誤差，但是在船舶編隊中每艘船舶必須時刻與領航者保持通信，導致船舶之間的通信數據對編隊的形成沒有起到相應的效果，從而造成通信資源浪費。

在多船舶或多智能體的協調控制中，通信問題相對復雜[8]。間歇通信包含了正常通信時段和通信缺失時段，外部環境干擾可能會導致間歇通信的出現，同時在通信時主動采用間歇性的通信過程并設計合適的控制器，可以在保證理想通信效果的前提下減少一定的通信帶寬，從而減少通信設備的損耗。Gao等[9]提出了事件觸發間歇通信環境下AUV的編隊控制問題，并將有限時間理論與控制器設計相結合，但是編隊的魯棒性較差，當某一AUV失去與領航者的通信后，不能通過獲得其他AUV的信息實現編隊。Wen等[10]提出了一階線性多智能體在間歇通信下的一致性問題，并推廣到編隊及切換拓撲的一致性跟蹤問題，但是并沒有給出具體的通信時長約束條件。徐律等[11-12]設計了二階多智能體在間歇通信環境下的一致性控制律，且考慮了延時等因素,但是卻未考慮到多智能體受到干擾后，其穩定性的充分條件的判別標準也會隨之變得復雜。Wen等[13]在考慮外部干擾下提出了二階智能體的一致性協議。上述文獻針對的都是雙積分為主的模型，與實際船舶的模型相差較大，在對船舶進行研究時，推導過程會產生其他復雜的項，所以以多智能體為主的文獻成果并不能很好地應用到實際船舶中。

基于以上問題，本文將對間歇通信環境下的船舶編隊控制問題進行研究。首先，將圖論與反步法相結合，采用誤差觀測器處理干擾誤差，設計正常通信時段的控制律。然后，考慮通信缺失的時段，設計船舶控制律，推導出新的充分條件并予以證明，在確保合適的通信時長情況下，實現多艘船舶的編隊。最后，將李雅普諾夫函數作為判斷系統穩定性的常用工具，通過其導數直觀反應系統的穩定性，構造李雅普諾夫函數從理論上證明每個跟隨者都能指數收斂到理想的編隊位置，并給出仿真驗證。

1 基本概念

1.1 圖 論

1.2 間歇通信定義

1.3 船舶數學模型

通常船舶在海平面的運動需要考慮3個自由度：縱蕩、橫蕩和艏搖。在船體坐標系下，3個自由度的船舶運動模型可表示為

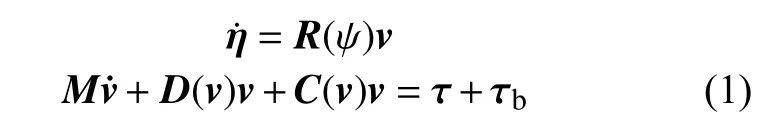
式中：η=[n,e,ψ]T，為在大地坐標系下的北方向位置、東方向位置、艏搖角；v=[u,v,r]T，為船舶在船體坐標系下的縱蕩、橫蕩和艏搖角速度；R(ψ)為大地坐標系與船體坐標系的轉換矩陣；M為質量矩陣；D(v)為阻尼矩陣；C(v)為科里奧利向心矩陣；τ=[τu,τv,τr]T，為控制輸入向量；τb=[τbu,τbv,τbr]T，為包含海浪、風等的時變外部干擾，且假設干擾是有界并連續的。對船舶模型進行變換，可得：

2 主要結果

2.1 船舶編隊控制律設計

2.2 間歇通信環境下的船舶編隊

本節綜合考慮間歇通信環境下的船舶編隊問題，設計了船舶編隊控制律式(18)，使以式(2)為模型的船舶能夠根據理想航跡的位置、速度信息以及相鄰船舶的信息形成編隊。此外，考慮到誤差觀測器的工作，在設計沒有信息交流的控制律時需要區別于一般的間歇通信。

3 仿 真

本節給出仿真圖來證明本文設計的船舶編隊控制律的有效性。假定一共有4艘船舶和1艘虛擬領航者，船舶模型采用Cybership II[15]。仿真的各項參數如下所示。

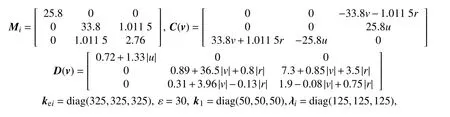
外部環境干擾誤差：

ρi(t)=[500sin(t),1200,100cos(t)]T

此外，船舶編隊的通信拓撲如圖1所示，并且假定船舶在通信時獲得的信息是實時且準確的。

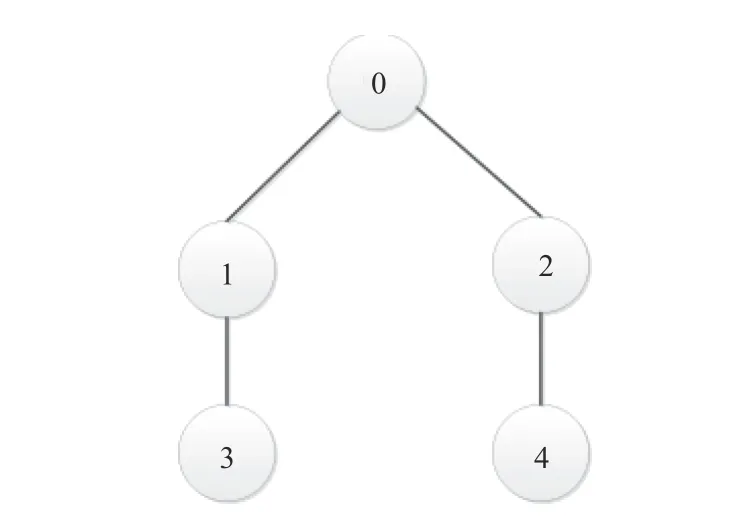
圖 1 船舶通信拓撲圖Fig. 1 Vessels communication topology

根據圖論可知，通信拓撲圖1包含虛擬領航者的拉普拉斯矩陣為

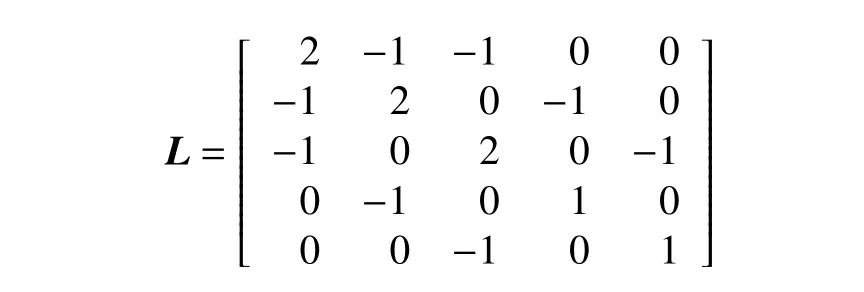
船舶編隊軌跡如圖2所示。由圖可看見，在采用本文給出的控制律并滿足通信時長的情況下，船舶能夠形成編隊。

每艘船舶的位置曲線如圖3所示。由圖可見，隨著時間的推移，4艘船舶的軌跡向量最終會收斂到理想值。

每艘船舶的速度曲線如圖4所示，可以看出，當控制律切換到不通信狀態時，船舶的速度保持不變，恢復通信后，船舶速度可以繼續跟蹤理想速度。

由圖2可見，每艘船各自擁有不同的初始位置，在控制律式(18)的作用下，最終形成理想的編隊并且收斂到指定的軌跡，由于需要在控制中切換觀測器函數和船舶的控制律，所以導致在不通信時段船舶航行軌跡會有一定程度的誤差（圖3和圖4），但是當下一個通信周期到來時，船舶可以重新回到理想的軌跡并保持理想狀態。

圖5為船舶的位置跟蹤誤差，圖6為船舶的速度跟蹤誤差。由圖5和圖6可見，在通信時段，船舶位置和速度跟蹤誤差會收斂到0，并且通過采用合適的控制律可以保證誤差快速收斂到0，同時增大通信時間，也可以保證編隊的穩定形成。

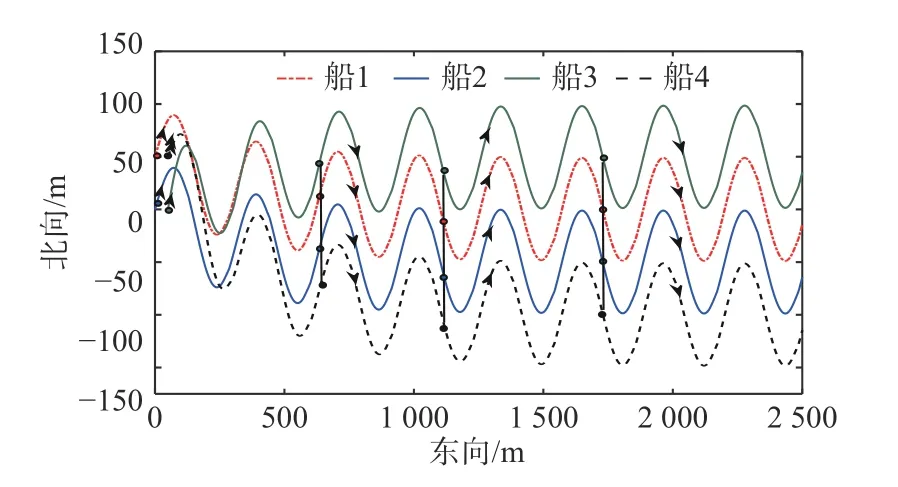
圖 2 船舶編隊軌跡Fig. 2 Formation trajectories of vessels

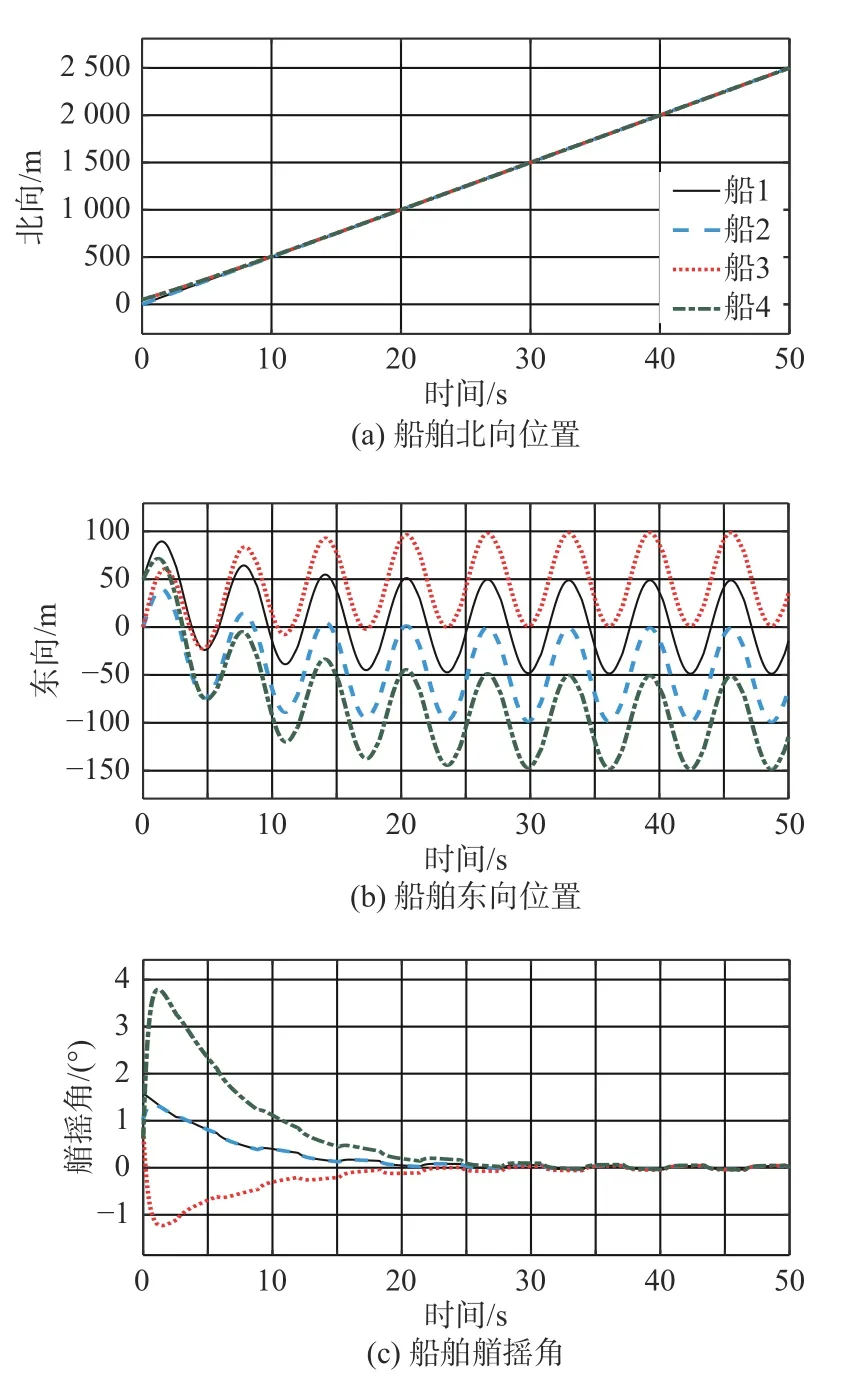
圖 3 船舶位置曲線Fig. 3 Position curves of vessels

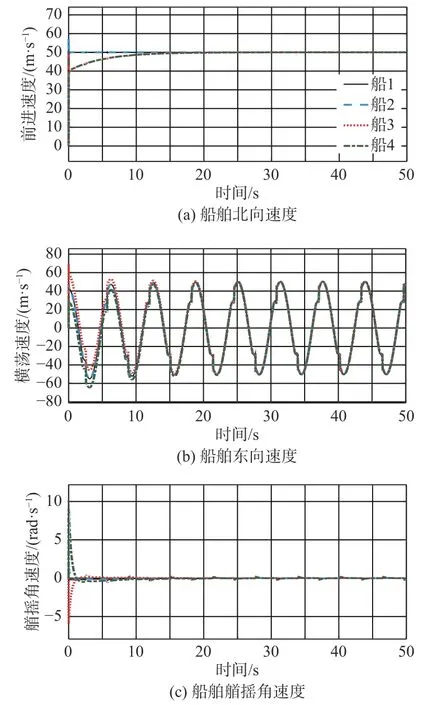
圖 4 船舶速度曲線Fig. 4 Velocity curves of vessels

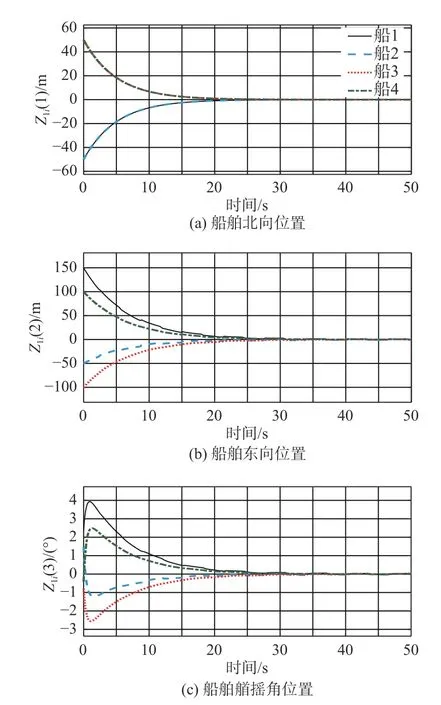
圖 5 船舶位置跟蹤誤差Fig. 5 The position tracking errors of vessels

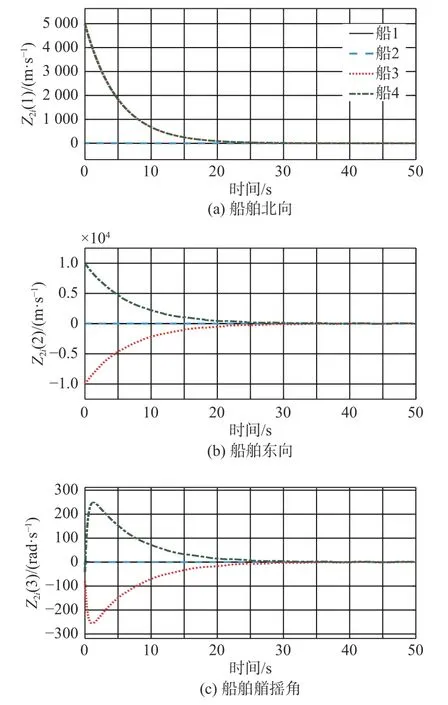
圖 6 船舶速度跟蹤誤差Fig. 6 The velocity tracking errors of vessels

4 結 語

本文研究了在間歇通信環境下的多艘船舶的編隊控制問題。考慮了實際環境中存在的外部干擾，加入誤差觀測器來觀測外部干擾。在正常通信時段，基于圖論和反步法設計編隊控制律，將船舶和虛擬領航者之間的理想相對位置和速度信息作為輸入，設計的控制律可以使每艘船舶到達理想的位置。在通信缺失時段，只需要利用船舶的自身信息設計控制律，給出滿足編隊形成的充分條件并予以證明。利用李雅普諾夫方程，對所提出的控制律的穩定性進行嚴格的分析，保證船舶編隊以指數形式收斂到理想位置并跟隨理想軌跡。未來將考慮對間歇通信中存在的延時、噪聲等問題進行研究，使之具有更廣泛的意義。